拓扑声子晶体

彭 湃,刘正猷

(1.中国地质大学(武汉) 数学与物理学院，湖北 武汉 430074；2.武汉大学 物理科学与技术学院 教育部人工微纳结构重点实验室，湖北 武汉 430072)

声子晶体是具有空间周期性的人工结构材料，质量密度及弹性常量在空间周期性排列. 声子晶体拓扑性质的研究受到越来越多的科研工作者的关注. 本文从声子晶体的背景出发，介绍了其研究进展.

1 声子晶体的研究背景

1.1 声子晶体的概念

其概念源自自然晶体(固体)——原子在空间中周期性排列，是自然晶体的拓展. 根据固体物理学中的能带理论，当电子在晶体中运动时受到晶格的布拉格散射形成带隙或禁带，在禁带内电子态不能存在. 能带理论预言了导体、绝缘体和半导体并说明了它们的区别. 由于波动现象的一致性，在上世纪90年代，人们将电子体系中“利用晶格的周期性操控电子传输”的概念拓展到经典体系“利用周期性人工结构操控光/声波在其中传播”. 1987年，Yablonovitch[1]和John[2]分别提出了光子晶体的概念并于1991年得到实验验证[3]. 1993年，声子晶体的概念被提出并得到实验验证[4-12]. 声子晶体通常可由散射体(例如钢球)周期性排列在另一种基体材料(例如水)中形成，声波在基体中传播会受到周期性排列的散射体的布拉格散射作用，从而形成类似电子带隙的“声子带隙”. 频率在带隙范围内的声波无法在声子晶体中传播. 由于声波一般难以与电场或磁场相互作用，有效操控声波的手段有限. 声子晶体的出现为操控声波、设计全新声学器件提供了可能性.

1.2 声子晶体的发展和优势

声子晶体的发展得益于近几十年计算机计算能力的大幅提升. 区别于自然晶体的基本构筑单元(1个或数个原子)以及结构，不能随意“加工”，这由材料的稳定性决定. 声子晶体具有宏观结构，因而易于加工. 可运用现有的成熟加工工艺和技术，例如微纳刻蚀工艺或3D打印技术，制备和加工声子晶体. 通过改变散射体的大小和形状[7]，在散射体内部引入更小的次级结构[8]，或者改变散射体之间的连通性[9]，都能够改变声子晶体的能带结构和声学性质. 在现代加工技术的帮助下，声子晶体因其低廉的制备成本和广阔的设计空间受到广泛关注并得到大力发展.

计算声子晶体能带及波函数有多种方法. 平面波方法是最早被提出并用来计算声子晶体能带结构. 其要点是把波函数做平面波展开，把周期性结构做傅里叶展开. 当散射体形状为规则的球/圆柱型时，用多重散射理论(Multiple scattering theory, MST)将声波波函数在球/柱坐标下展开，可使计算非常快捷和方便. 当散射体为复杂形状(例如矩形或三角形)时，取而代之的是用时域有限差分(Finite difference time domain, FDTD)或有限元 (Finite element method, FEM)等数值计算方法，将空间离散化后用计算机进行仿真模拟，最终得到能带结构、声场分布等结果. 例如，比较流行的商业软件COMSOL Multiphysics，就是采用的有限元法.

对声子晶体的研究大致经历了3个阶段. 第一阶段主要致力于获得宽频带隙[4-9]，希望利用带隙实现隔振降噪、防震等功能. 其中重要的发现是，含有共振单元的声子晶体能产生低频带隙[8]，在环境噪声控制、声隐身、地震防护等诸多方面具有应用前景. 第二阶段主要关注声子晶体的通带[10-12]，通过通带设计实现对声波传输行为的操控，制作具有如聚焦、负折射、定向辐射等功能的声学器件. 特别地，对于低频通带，在波长远大于晶格常量的条件下，声子晶体可视为均匀材料，可用有效介质理论(Effective medium theory, EMT)提取其有效声阻抗、有效波速、有效质量密度及有效弹性参量等材料参量. 第三阶段也就是近来开始关注在前两阶段不太受重视的声场形态和相位信息，从而掀起了对声子晶体拓扑性质的研究热潮[13-36].

2 拓扑声子晶体概述

2.1 拓扑绝缘体的背景知识

拓扑绝缘体是一种不同于常规绝缘体的新物态. 拓扑绝缘体内部绝缘但表面能导电，并且表面电流具有鲁棒性，不会被杂质或缺陷散射. 这种优异的传播特性具有重要应用前景. 从能带结构上看，跟常规绝缘体一样，拓扑绝缘体也具有体禁带. 不同的是，对有限大小的拓扑绝缘体而言，能带结构上会出现跨越整个体禁带的、无能隙的表面态色散，即在表面上存在表面态. 对拓扑绝缘体施以连续的变化，例如让其结构变形，只要其体带隙不闭合，表面态就不会消失，拓扑绝缘体的特性就不会改变，表现出鲁棒性. 从数学上，几何形体在连续变形下的不变性就是几何对象的拓扑属性，由拓扑指数描述. 对材料拓扑属性的认识要归功于1982年Thouless等人对量子霍尔效应的研究[13]. 低温二维电子气在垂直外加强磁场下，体绝缘而边界导电，其霍尔电导是量子化的、具有鲁棒性的常量. 经典图像对量子霍尔效应中边界态的形成可按图1理解. 在外加垂直磁场后，内部电子在洛伦兹力的作用下做“圆周”运动，没有净电流. 而处于边界的电子不能形成完整的回旋，只能沿着边界做“半圆周”运动并向前形成表面电流. 显然，无论表面上是否设有障碍，表面电流只能单向流动，而不会反向.

图1 量子霍尔效应

Thouless等首次发现量子化的霍尔电导与二维电子体系能带的拓扑性质相关. 能带的拓扑性质可由拓扑指数——陈数 (Chern number) 描述，陈数定义为与能带波函数相关的贝利曲率(Berry curvature)在布里渊区上的积分，描述了能带的拓扑不变性. 陈数是整数，为 0时称为平庸的，刻画常规绝缘体；不为0时称为非平庸的，描述拓扑绝缘体. 这样，拓扑概念进入了物理，而对材料拓扑性质的研究成为凝聚态物理的重要方向. Thouless等也因此于2016 年获得诺贝尔物理学奖. 拓扑绝缘体表面态的鲁棒性归根结底来源于拓扑材料能带的拓扑不变性，或者说是受到了拓扑保护.

2.2 光/声系统的量子霍尔效应

在光/声子晶体中可观察到光/声波的类似电子的量子霍尔效应. 2005年，Haldane和Raghu首次在理论上提出了用旋光效应来实现光波的拓扑现象[14-15]. 并且在理论上指出一种通用方法：先在光子能带中构造二重简并的线性色散关系，即狄拉克锥(Dirac-cone),再通过打破时间反演对称性将简并打开，就能实现光的量子霍尔效应. 2014年Fleury 等人将这种思路引入声学系统[16-17]. 由于声波几乎不受磁场的影响，在声学体系中打破时间反演对称性需要采用类似图2(a)中的设计，给散射体增加环形腔并引入环形气流. 将低噪声的小风扇放置在环形腔中可作为有手征性的环形声源. 在弹性波体系中打破时间反演对称性则可以直接利用固体的转动. 如图2(b)所示，Nasha等人在2015年将同方向旋转的陀螺仪用弹簧连接成六角蜂窝状的机械网络[18-19]. 周期性的排列使整个机械网络具有弹性波的带隙，从而在边界上支持一定频率范围的表面模式，类比量子霍尔效应中的表面电流. 如图2(c)所示，陀螺仪的“晃动”只会沿机械网络的边界传导而不会影响到网络内部的陀螺仪单元，直观地展示了受拓扑保护的边界态的传输行为.

(a)环形气流结构单元[16] (b)陀螺仪单元[18]

(c)边界传播模式[18]图2 流体/机械拓扑声子晶体

2.3 拓扑声子晶体的分类

经过几年的系统研究，声子晶体拓扑态研究已取得了很大进展. 到目前为止，拓扑声子晶体除了绝缘体一大类型外，还包含半金属一大类型. 绝缘体类型可分为能谷绝缘体、一阶拓扑绝缘体(包含上述量子霍尔效应类型)、高阶拓扑绝缘体等几种子类型. 半金属态指的是能带结构中相邻能带以点、线或面的几何形态相接或简并. 以点相接或简并的包含狄拉克(Dirac)半金属和外尔(Weyl)半金属. 以线相接或简并的称为节线(nodal lines)半金属，以面相接或简并的称为节面(nodal surfaces)半金属. 以下以本课题组在能谷声子晶体(绝缘体态)和外尔声子晶体(半金属态)的研究工作为代表介绍2类拓扑态.

3 能谷声子晶体

3.1 二维声子晶体中的狄拉克锥色散关系

狄拉克锥是一类具有特殊形状的能带结构，在二维体系中表现为2条能带线性相交于一点，称为狄拉克点，从而在动量空间中张出圆锥状的色散曲面. 这种线性色散关系对应狄拉克方程的无质量相对论粒子，后来在二维材料石墨烯中被实际观察到. 所以石墨烯中电子表现为无质量的相对论粒子，在理论和应用方面都具有重要意义. 通常以狄拉克锥色散关系作为出发点，通过解除狄拉克点的简并打开带隙来研究系统非平庸的拓扑性质. 研究已发现，二维声子晶体中也存在类似石墨烯的狄拉克锥色散关系或能带[20-23]，以这类声子晶体为出发点是寻找拓扑声子晶体的有效途径. 2015年，用基于群论的“k-p微扰方法”得到产生狄拉克锥的条件[24]，可看到其存在依赖于体系的对称性. 所有能形成狄拉克锥的声子晶体种类总结为表1. 表中的对称性指点群，“偶发性” 和“确定性”表示狄拉克锥的形成是必然的还是偶然的.

表1 晶体不同对称性对应的狄拉克锥

3.2 声子晶体中的能谷态与谷边缘态

从表1中可以看出：由正三角形柱体按六角晶格排列构成的声子晶体，且当三角形的取向角α=0°时[见图3(a)]，可以确定拥有狄拉克点，同时结构又最简单[25-26]. 该声子晶体的能带结构如图3(b)中黑线所示，在布里渊区角点(K点和K′点)形成狄拉克锥. 实验上将有限厚的正三角形 PMMA(聚甲基丙烯酸甲酯)柱夹在2块PMMA 板之间，当声源频率足够低时夹板间只有零阶波导模式存在，从而保证本质上是二维体系[见图3(a)]. 如果将正三角柱逆时针旋转小角度(转角α=10°)，则体系的对称性从C3v降至C3，狄拉克点的简并被打开，形成图3(b)中红-蓝线所示的2条能带，中间由带隙隔开.

相比引入环形气流打破体系时间反演对称性打开狄拉克点简并的做法，这里是通过旋转散射体打破体系的镜面对称性来打开带隙. 在带隙打开处，上能带的极小值和下能带的极大值位置，通称为能谷. 不管是上能谷还是下能谷，都成对出现在K点和K′点，即原来的狄拉克点位置. 成对的能谷态可视为赝自旋，对应于2个自旋取向. 能谷赝自旋为声场调控提供了新的自由度. 这类具有能谷态的声子晶体称为能谷声子晶体. 在K点的能谷态K2和K1的本征场分别如图3(c)右边的上下插图所示，颜色表示声压场的强度，箭头表示能流场的大小和方向. 可以看出，K2和K1的能流场表现为手征性的涡旋场，分别按顺时针和逆时针取向. 相应地，与K2或K1态成对的、位于K′点的能谷态也是涡旋态，但涡旋方向正好相反. 涡旋声场具有角动量，当颗粒置于声场中时，声场的角动量可转化为作用在颗粒上的力矩，从而可实现对颗粒操控. 可以想见，如果将散射体顺时针旋转同样角度(即α=-10°)会得到完全相同的能带结构，但是能谷态K2和K1会发生反转. 图3(c)展示了K点处这2个能谷态(红色为逆时针涡旋即正涡旋q+，蓝色为顺时针涡旋即负涡旋p-)的频率随转角α的变化情况. 可以看出，当转角为正时，上能谷K2是负涡旋，下能谷K1是正涡旋；当转角为负时，上能谷K2变成负涡旋，下能谷K1变成正涡旋，即发生了能带反转. 在特殊转角0°和±60°时，K2和K1态是简并的，即能带为狄拉克锥的情形.

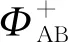
(a)能谷声子晶体样品 (b)能带结构

(c)谷态频率随转角变化 (d)谷边缘态能带结构

(e)谷边缘态的无障碍传输图3 能谷声子晶体

3.3 能谷声子晶体的研究新进展

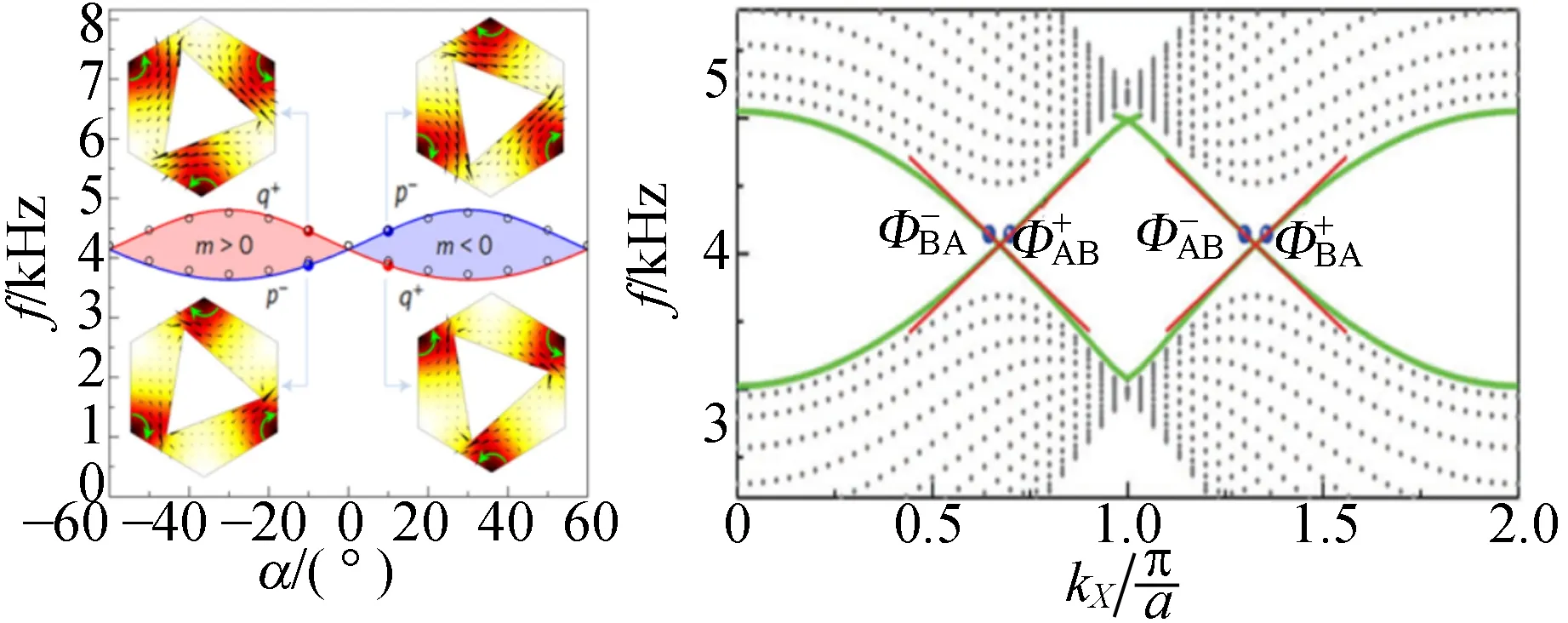
能谷声子晶体的研究已取得了很多进展[27-33]. 例如包含丰富拓扑相的双层能谷声子晶体[27-28]，水声背景下的能谷声子晶体[32]，以及基于四方晶格的能谷声子晶体[33]等. 下面重点介绍关于能谷声子晶体中的拓扑体态运输[29]和拓扑声子晶体芯片[30]的相关研究. 如何将存在于界面上的拓扑谷边缘态拓展成宽度可调，即具有宽度自由度的拓扑谷波导态？可采用如图4(a)所示的设计，由转角不同的声子晶体组成“三明治”结构. 外面2层(A层和B层)是具有拓扑带隙的能谷声子晶体，其转角分别选为α=30°和α=-30°，以提供最宽带隙；中间新增的夹层(C层)是无带隙的声子晶体(转角α=0°)充当波导管.

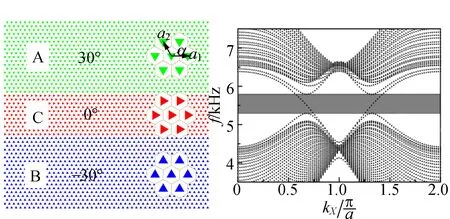
(a)异质结构 (b)X方向投影能带结构

(c)不同缺陷下的压强分布图4 能谷声子晶体的拓扑波导运输

如图4(b)所示，如同前述只有A/B界面的情形，在A和B的公共带隙内，体系存在1条跨越带隙的拓扑非平庸的谷波导态，来自声子晶体A和B之间的非平庸边界态与声子晶体C的平庸体态的耦合. 谷波导态也具有和边界态类似的鲁棒性. 图4(c)展示了被点源激发的谷波导态在波导管中传播的情形. 无论是在波导管中引入无序，或者引入凸起、凹陷或两者同时存在，都不会影响谷波导态的传输，表现出强大的鲁棒性. 借助于边界态和体态的耦合，原本只出现在边界上拓扑界面波现在“充满”了整个波导管. 和边界态传输相比，这种波导态传输的优势在于：具有宽度的波导管更容易和已有器件对接从而方便于应用；波导管更有利于能量传输.

能谷态不仅存在于前述流体(空气)体系，也能存在固体体系. 运用微纳刻蚀工艺在硅片上制备出片上能谷声子晶体[30]. 如图5(a)所示，由底部薄板和在其上刻出的正三角柱阵列构成. 体系支持多种振动模式的 Lamb 波传播，其中的弯曲波(面外振动)模式便于激发，其运动方程和二维声波的波动方程类似. 按六角晶格排列的正三角柱阵列可对弯曲波进行调制，形成狄拉克锥色散. 与前面类似，可通过旋转正三角柱打开狄拉克锥形成带隙，产生能谷. 图5(b)显示在K点的能谷，实线为理论计算的能带，颜色表示相应的实验结果，两者一致. 这里同样利用了打破镜面对称解除狄拉克点简并的机制. 图5(c)为能谷态K2和K1的本征场在不同时刻的形态，表现为按顺和逆时针旋转的螺旋态. 图5(d)展示了在2个转角相反的能谷声子晶体相的界面上传播的谷边界态，在拐弯处没有反射，具有鲁棒性.

(a)片上能谷声子晶体 (b)面外模式能带结构

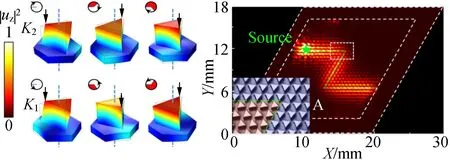
(c)3个时刻的上下能谷态本征场 (d)拓扑边界态传输图5 硅片的能谷声子晶体

获得拓扑保护的谷边界态的过程可以概括为：找到狄拉克锥→降低对称性打开带隙,得到能谷→实现能带反转→用能带反转的2个晶体构造界面→获得界面上的谷边界态. 通过破缺体系对称性打开狄拉克点简并是构造拓扑声子晶体的常用方法，该方法也适用于三维体系[34].

4 外尔声子晶体

4.1 声子晶体中的外尔点

三维声子晶体的能带结构中存在和前述二维狄拉克锥类似的线性色散关系，其中的2度简并点称为“外尔点(Weyl point)”. 与二维体系中的狄拉克点沿平面任何方向均为线性色散不同，三维体系中，从外尔点出发沿三维空间3个方向都为线性色散关系. 外尔点简并不像狄拉克点简并那样容易打开，具有很强的鲁棒性. 如果连续变形其晶格，只会看到外尔点在倒空间游弋，看不到外尔点简并的打开. 外尔声子晶体于2017年在实验上实现[35]. 图6(a)展示了用3D打印技术制作的外尔声子晶体样品的外貌及细节，插图为单胞的示意图.

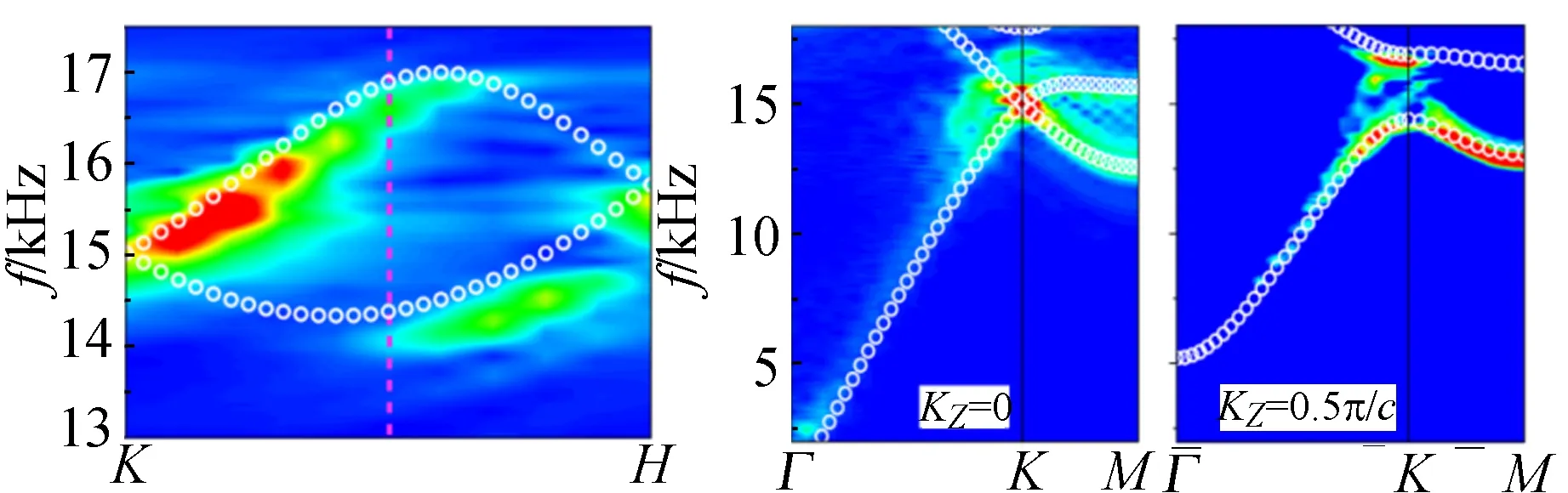
图6(b)显示该外尔声子晶体的布里渊区及外尔点在其中的分布，紫点和绿点分别表示拓扑荷为+1和-1的外尔点. 在倒空间用球面包住外尔点，通过球面上的波函数计算出球面上的贝里曲率矢量，把贝里曲率在球面上做积分即得到外尔点的拓扑荷. 贝里曲率矢量如同磁感应强度矢量，对应有不为零的矢势[即贝里连接(Berry connection)]. 但贝里曲率的球面积分(即拓扑荷)不为零，所以外尔点的拓扑荷如同“磁荷”. 图6(c)为布里渊区边界上沿kZ方向的能带结构，可见在布里渊区的K点和H点处2条能带线性相交，在K-H之间2条能带分开，具有带隙. 图6(d)为给定kZ时kX-kY平面内的能带结构. 当kZ=0时(左图)能带线性相交于K处形成前节所述的狄拉克锥，当kZ偏离0时(右图)2条能带打开带隙. 这清楚表明K点是外尔点. 同样分析可知道H点也是外尔点，当然K′和H′也是外尔点. 外尔声子晶体具有奇妙的性质，其表面存在拓扑表面态，而且表面态的等频线不闭合，表现为一段一段的弧，称为“费米弧(Fermi arc)”，而普通表面态的等频线都是闭合的. 以外尔声子晶体的XZ表面为例，如图6(e)中左图所示，如果把点源(频率约15 kHz)放置在表面中心，可看到表面态被激发出来并在表面上传播. 如果把表面上的场分布做傅里叶变换，可以得到表面态的等频线，如图6(e)右图所示. 可以看到等频线确实不闭合，而是一段一段的费米弧，连接外尔点在这个表面的布里渊区的投影(紫色和绿色点). 图中颜色是实验结果，白色是数值计算结果，其中实线为该表面上的表面费米弧，虚线为对面表面上的表面波费米弧. 可以看到实验和数值结果一致. 费米弧表面态也具单向传输、抗缺陷的特性. 图6(f)(为Z方向的俯视图)显示了在XZ表面激发的表面波(具有kZ=0.5π/c，c是Z方向的晶格常量)的传播. 可以看到它只向左传播，在传播到左角点后，拐入YZ表面，继续向上传播. 虽然在YZ表面故意制造了凹槽缺陷，可以看到表面波翻越这一障碍继续向上传播，表现出强大的单向传输特性.

(a)外尔声子晶体样品 (b)布里渊区及外尔点分布

(c)kZ方向能带 (d)kX-kY平面上的能带结构

(e)XZ表面上的能带结构

(f)费米弧表面态的无障碍传输图6 外尔声子晶体

4.2 拓扑表面波的负折射效应

三维外尔体系中的表面波的传播由费米弧的形状及取向决定. 调控费米弧即可调控表面波的传播. 下面在另一个外尔声子晶体中显示费米弧对表面波传播的调控. 新的外尔声子晶体如图7(a)所示[36]，是更简单的柴堆结构. 第1层是方柱的一维排列，第2层是把第1层旋转120°，第3层是把第2层旋转120°，如此类推，形成三维结构. 这一体系同样在布里渊区的K点存在外尔点. 从图7(a)的左图中可以直观看到，选择不同的表面切割位置会使样品的表面结构发生变化，表面结构的差异会导致表面态的能带不同，即费米弧发生变化.

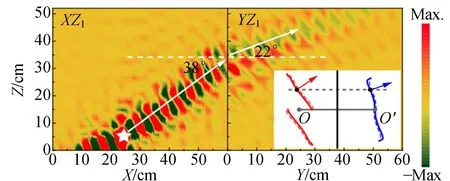
图7(b)为切割的实验样品的外观，四周有4个表面，其中相邻3个表面记为XZ1(正面)、YZ1(右侧面)和XZ2面(背面). 正面和右侧面的表面费米弧如图7(c)中上图的插图所示. 图7(c)中下图的插图显示右侧面和背面的表面波费米弧. 图7(c)中场图为实验测量结果，可以看到表面波在XZ1面激发，传播至与YZ1面的交界时完全进入YZ1面，不发生反射，在YZ1面上传播时改变了方向. 不管是在XZ1面还是在YZ1面，表面波的传播方向完全由费米弧控制，即按费米弧的梯度即法线方向传输. 可以看到，从XZ1面到YZ1面，在YZ1面折射波与在XZ1面的入射波，位于两面交线的法线的两侧，是正常的折射. 但是，继续来看表面波从右侧面YZ1面进入背面XZ2面的折射，如图7(c)下图所示，结果大不相同. 可看到在XZ2面的折射波与在YZ1面的入射波位于两面交线法线的同一侧，即发生了负折射.

(a)结构示意图及单胞 (b)实验样品

(c)费米弧表面态在棱边处的拓扑折射图7 外尔声子晶体表面态的拓扑负折射

5 结束语

介绍了本课题组近几年在拓扑声子晶体领域的一些研究进展，并以此为案例介绍拓扑声子晶体的前沿动态. 拓扑声子晶体能支持类似量子霍尔效应中边界电流的、受拓扑保护的、具有鲁棒性的界/表面波. 拓扑界/表面波的核心在于构建出连接体带隙上下体带的无能隙的边界态. 在能谷声子晶体中是通过打开狄拉克锥获得能带发生反转的2个谷拓扑相，在其界面获得能谷锁定的拓扑边界态. 在外尔声子晶体中则是借助1对拓扑荷相反的外尔点来形成费米弧表面态. 拓扑界/表面波的鲁棒性表现在对缺陷和无序免疫，具有单向传输的性质. 这种无障碍的传输特性无疑具有广阔的应用前景，也激发了科研工作者对拓扑物理的极大兴趣.