激光斑点漂移的研究

宋胤彤，张哲伦，李尊祺，刘国超

(北京大学 物理学院，北京 100871)

2020年IYPT的第11题为Drifting speckles[1]. 将激光束照射到黑暗的表面，在斑点内可看到颗粒状的图案. 请解释现象并且研究漂移取决的相关参量. 当通过相机或者人眼观察时，颗粒状的图案在缓慢移动. 本文描述了激光散斑的漂移现象，研究了激光散斑漂移现象的成因，通过理论计算给出散斑漂移速度的依赖因素，并通过实验检验.

1 散斑漂移现象简介

用激光照射墙表面时，直接用人眼或者利用相机可以观测到颗粒状的细小斑点，这些细小斑点(图1中的白色颗粒)即为激光散斑. 图1中散斑呈现白色是相机曝光过度导致的(实验中发现，曝光不足时无法清晰观测到圆斑和散斑，故实际操作时调节曝光使散斑略微过曝)，由人眼观测可以发现散斑仍然为红色. 为方便区分，下文中的散斑指中心圆环内的白色细小颗粒，圆斑指外侧圆形的红色斑点.

图1 利用相机拍摄的激光散斑

当人眼或相机移动时，可以观测到散斑相对于圆斑的运动，这种运动即为本文研究的散斑漂移现象. 通过简单的实验，可以发现人眼或相机垂直于光屏移动时无漂移现象，而平行于光屏移动有散斑漂移现象. 在实验中也可以发现这种运动是和相机的运动同时发生的,因此，可以通过测定相同时间内散斑、圆斑和相机的位移得到三者的速度关系.

2 散斑漂移现象的理论解释

2.1 散斑的形成机理

激光照射在粗糙表面(表面起伏程度远大于激光波长，常见表面均满足)上发生漫反射，可以等效为表面上存在若干次波波源，次波波源的振幅相同，初相位则因受到表面影响而各不相同. 这些次波波源发出的波在空间中相干叠加，在相干增强处形成了观测到的散斑[2].

2.2 散斑漂移的定量解释

散斑漂移的示意图如图2所示. 由散斑的形成机理，散斑实际位置和圆斑所在位置(即光屏处)并不相同，在移动相机或人眼时，由于视差二者出现相对运动，形成漂移现象.

图2 散斑漂移的示意图

下面将分别利用几何光学和波动光学对漂移速度进行计算并说明其等价性. 为简化表达，示意图均为单个透镜的情形，实际上相机镜头应为透镜组.

2.2.1 将散斑漂移简化为几何光学问题

将相机的位置记为x，将相机屏上的圆斑和散斑的位置记为x″，以区分不同平面上的移动. 在之后的实验中也采用同样的标记方法.

对于单个透镜，可以根据图3计算漂移距离. 记物面到透镜(相机镜头)的距离为L，透镜到像面(相机成像区域)距离为f. 红线和蓝线分别表示移动前后的光路. 根据相似三角形，可得：

即有：

(1)

相机内部的透镜组相对位置是近似不变的，因此之后的成像与L无关，是由相机决定的近似不变的参量. 因此可以用常数近似描述之后的成像过程对移动距离的影响. 此处将L与f的乘积记为Mf，称之为相机参量，则(1)式对实际的相机可以写为

则散斑的漂移距离为

(2)

图3 散斑漂移的几何光学计算法

2.2.2 将散斑漂移简化为波动光学问题

考虑光的波动性质，利用基尔霍夫衍射积分进行计算. 设光屏上的复振幅分布为A(x,y)，透镜的前复振幅分布为Bi(x′,y′)，透射函数为t(x′,y′)，后复振幅分布为Bt(x′,y′)，相机底片上的复振幅分布为C(x0,y0)(x″,y″).u为物到相机镜头的距离(L或s)，v为相机镜头到相机底片的距离，F为焦距. 先考虑墙上某点产生的光场，由惠更斯-菲涅尔原理[3]有如下基尔霍夫积分：

(3)

(4)

(5)

当透镜光心位于(x0,y0)时，考虑光屏上所有点光场的叠加，得到相机底片上(x″,y″)处的复振幅[3]为

那么当透镜光心位于(0,0)时，考虑墙上所有点产生的光场的叠加，则底片上(x0″,y0″)点的复振幅为

如果忽略积分区域Σ1(0,0)和Σ1(x0,y0)的区别，并令Δx″=x″-x0″，Δy″=y″-y0″，则有：

|C(x0,y0)(x″,y″)|2=|C(0,0)(x0″,y0″)|2,

即

当透镜移动(Δxcamera,Δycamera)时，散斑的位移为

(6)

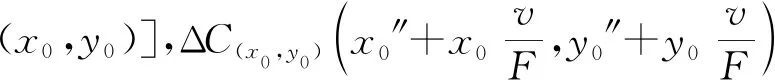
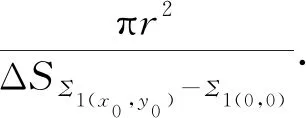
对理论的修正：考虑积分区域Σ1(x0,y0)和Σ1(0,0)的差别，则有：

其中,

由此可见，几何光学近似是合理的. 因此可以利用式(2)计算散斑漂移速度.

3 散斑漂移速度公式的实验检验

3.1 影响散斑大小的相关因素

由于在测定散斑漂移距离时，散斑的大小对测量的精度产生较大影响，因而有必要研究影响散斑大小的因素. 可以利用光强关联函数对散斑大小进行定性分析，得到散斑大小的影响因素.

光强关联函数为

这一函数用于描述相邻点光强的相关性，相关性越强代表散斑颗粒越大. 在实验中直接用CCD相机拍摄散斑[4]，利用Mathematica软件计算关联函数，结果如图4所示.

光强关联函数

其大小可以用与x轴围成的面积描述,其中w为高斯光束在散斑处的光腰. 可以发现，L越大关联函数值越大，即散斑颗粒越大. 而相机观测到的圆斑大小与L呈负相关.

图4 不同距离L拍摄的散斑计算得到的关联函数

综合分析，圆斑越大散斑越小，圆斑越小散斑越大. 这一结论有助于后续实验过程中对光路进行调节，得到更清晰、更易于测定的散斑图样.

3.2 散斑漂移的距离-相机移动距离的定量测定

实验中采用扩束透镜和聚焦透镜调节圆斑和散斑的大小，以便于测定. 使用λ=632.8 nm的氦氖激光器作为激光源，利用配置镜头的HY-2307型号CCD相机进行观测，并利用相关软件对观测结果进行计算.

3.2.1 标定相机参量Mf

保持视在漂移Δx″不变，测定相机位移Δx和相机聚焦距离s的关系，其斜率即为Δx″/Mf.

实验中保持Δx″=100 pix不变，测得的相机参量标定曲线如图5所示. 拟合曲线的斜率和截距分别为：k=0.023,b=-5 mm,r=0.999 53. 计算得到Mf=(4.302±0.044) pix.

图5 相机参量定标曲线

3.2.2 测定散斑漂移

在实验中分别保持相机与光屏距离L和相机聚焦距离s不变，改变另一参量，测定散斑位移量和圆斑位移量，计算得到散斑相对圆斑漂移/相机移动距离曲线，如图6～7所示.

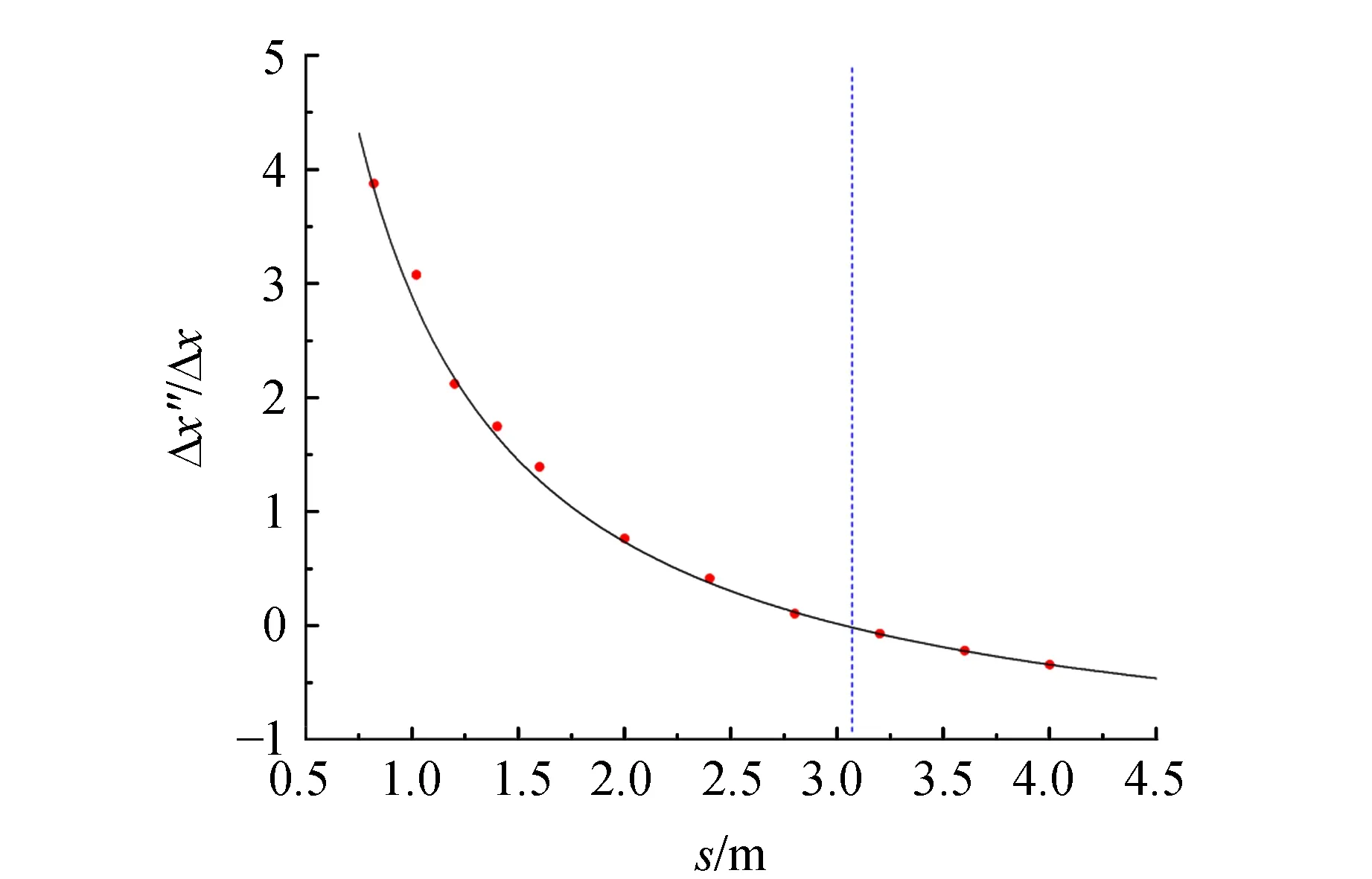
图6 L=3.070 m时的漂移/相机位移随相机聚焦距离的变化

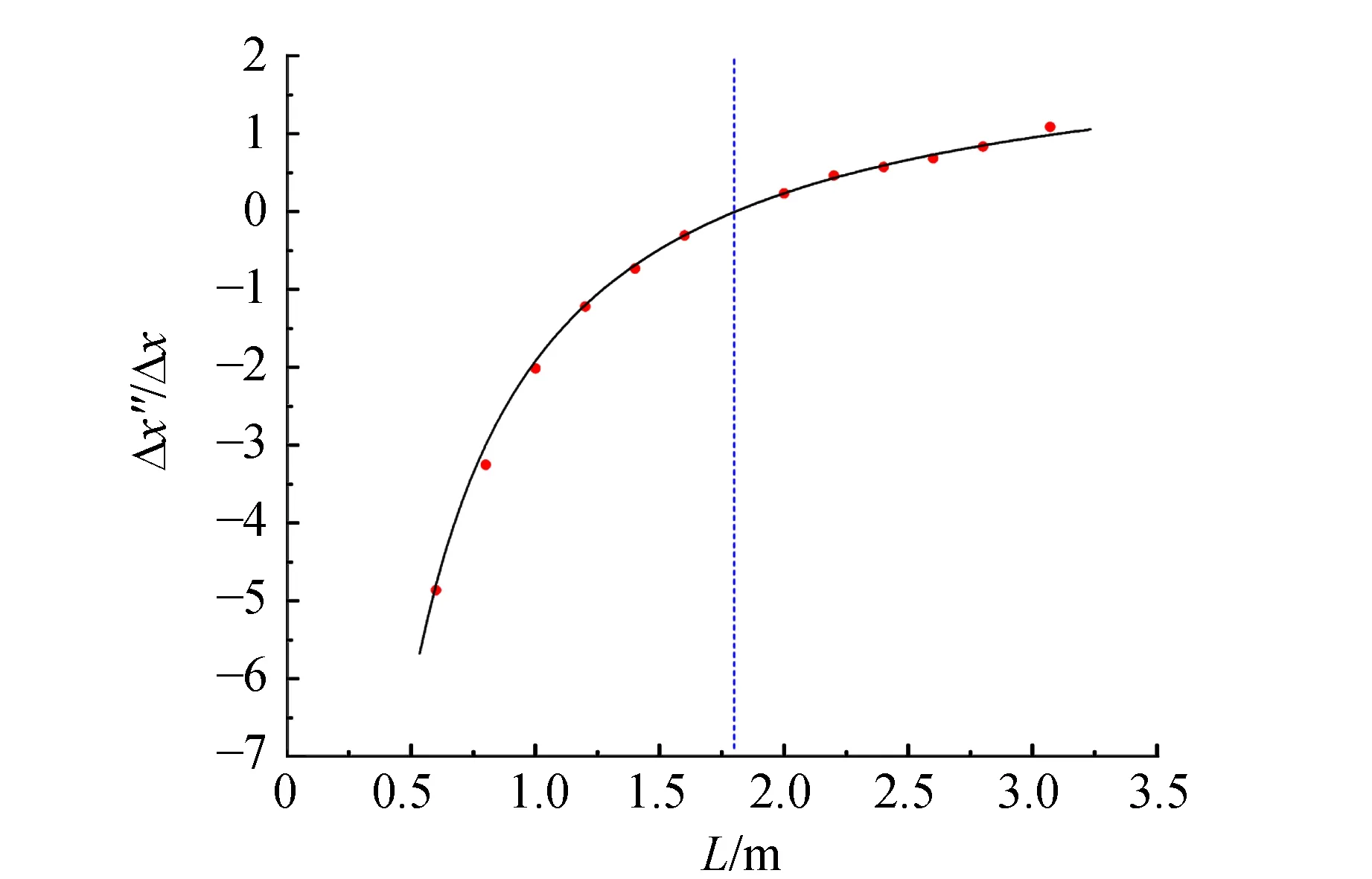
图7 s=1.800 m时的漂移/相机位移随相机与光屏距离的变化

利用理论公式对实验数据进行拟合，验证其符合程度.

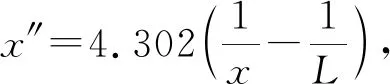
由此可验证理论公式(2)的正确性. 由于漂移运动是和相机的运动同时发生的，可以由移动的距离公式直接导出散斑漂移的速度公式为

(7)

3.3 实验误差分析

实验误差主要来源于对各项距离的测量误差和不稳定因素对散斑图样的影响.

3.3.1 距离测量带来的误差

1)通过米尺和桌面上设置的距离标尺测量L和s，测量误差为σ1=1 cm.

2)通过计算机上的S-EYE软件测量散斑移动和圆斑移动，在不考虑图案本身振动的条件下，散斑移动测量误差为σ2=0.1 pix，圆斑移动的测量误差为σ3=0.2 pix.

3)通过光具座上的游标测量相机移动，测量误差为σ4=0.1 mm.

3.3.2 散斑图样振动带来的误差

实验过程中，由于平台的振动、空气流动、激光光源本身发光的不稳定性，散斑并不总是静止的，而是会出现不规则的小幅度振动. 实验中通过控制空气流动、减少平台振动等方式减小散斑振动后，观测到小振动的幅度小于0.1 pix，因此其带来的误差主要影响散斑位置的确定(而散斑位置的变化与标定散斑位置的误差数量级相同，可以忽略). 这种影响带来的误差数量级小于散斑位置标定的误差，因此在本实验条件下可忽略.

4 结 论

致谢：感谢论文撰写过程与北京大学物理学院荣新老师的有益讨论！