一类摩擦振子现象的研究
2021-06-01史雨川樊代和刘其军贾欣燕
史雨川,樊代和,b,刘其军,b,贾欣燕,b,魏 云,b
(西南交通大学 a.物理科学与技术学院,四川 成都610031; b.物理国家级实验教学示范中心(西南交通大学),四川 成都611756)
摩擦振子(Friction oscillator)的研究是第33届IYPT的竞赛题目之一,具体内容为:1个大块的物体被放置在2个相同的平行水平圆柱体上. 2个圆柱以相同的角速度旋转,但方向相反. 题目要求研究物体在圆柱体上的运动如何依赖于相关参量[1].
与摩擦振子相关的研究已有报道. 李鑫等通过Algodoo仿真软件探究了摩擦振子的运动规律,运用理论分析和模拟验证,得到了运动所依赖的参量与轮轴间距、摩擦因数及初始位置有关的结论[2],但没有对理论结果进行实验验证. 袁路奇研究了摩擦振子系统中摩擦力产生的不同方式,得到了摩擦振子在振动中摩擦因数不停变化的结论[3]. 秦琅研究了一类非线性摩擦振子的周期运动,得到系统随参量改变具有不同类型周期运动的结论[4]. 杨绍普等研究了存在黏性阻尼时摩擦振子的运动状态,给出了纯滑动的精确解,并得到振动幅值的解析表达式[5]. 本文对IYPT赛题要求的摩擦振子现象进行理论和实验研究. 通过建立模型并做受力分析,得出了摩擦振子运动的状态方程,通过实验研究证明了理论分析的正确性,仿真模拟了各参量对摩擦振子的运动状态的影响.
1 理论分析
如图1所示,假设一密度均匀、质量为m的长方体,放置于中心距离为S的2个直径均为D的圆柱上. 当2个圆柱分别以顺-逆或者逆-顺时针且以相同的角速度ω旋转时,长方体形成一类摩擦振子. 为了详细分析摩擦振子的运动情况,建立图1所示的直角坐标系,OC表示长方体的质心.
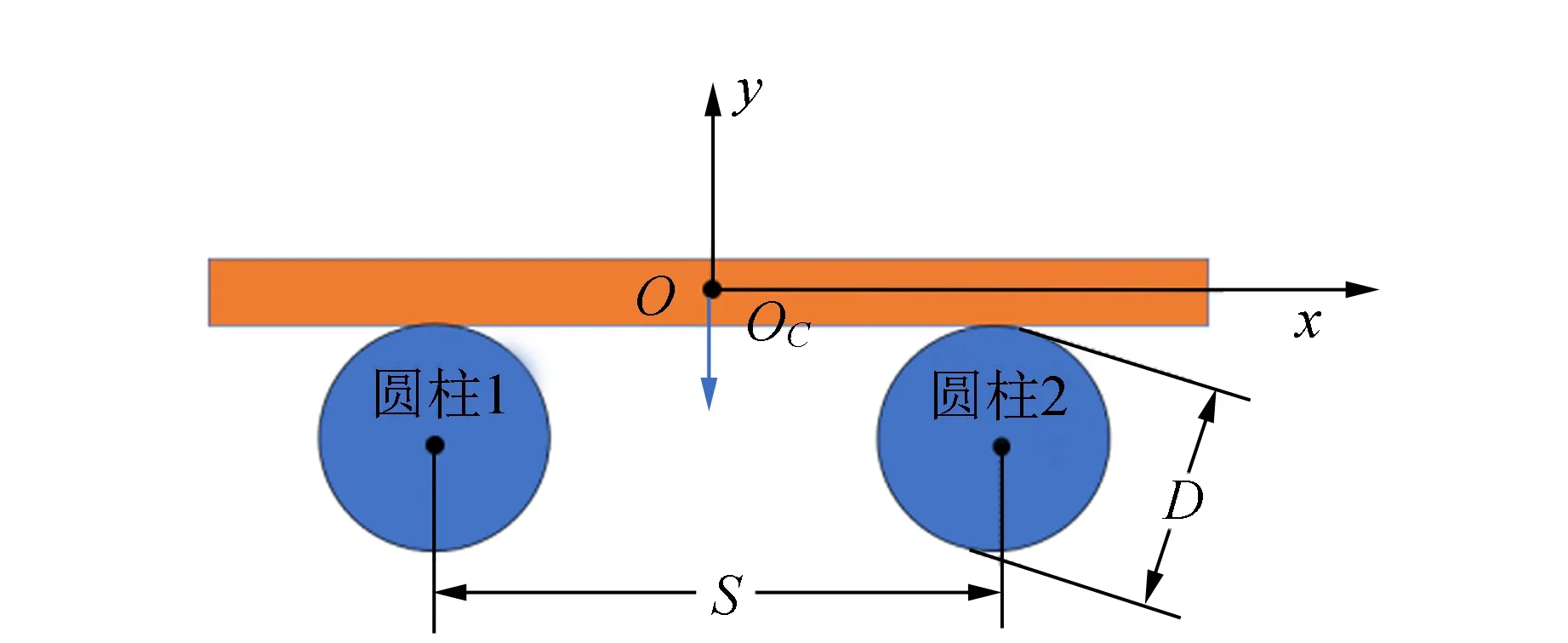
图1 摩擦振子模型示意图
1.1 圆柱1和圆柱2分别按照顺-逆时针旋转
当2个圆柱体以一定角速度ω旋转时,上方的长方体将做x方向的运动. 假设在某时刻t,长方体的质心OC偏离坐标原点的距离为x,如图2所示. 此时,在竖直方向上,长方体将分别受两圆柱所给支持力N1,N2以及重力mg. 运动过程中,长方体还将受到x方向的空气阻力f,以及圆柱体给的摩擦力fN=f1+f2.
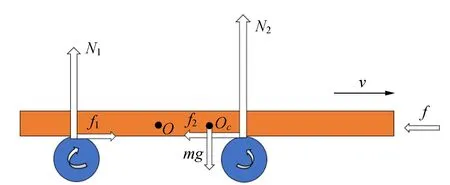
图2 长方体运动过程中某一时刻的受力分析图
分别将圆柱1、圆柱2作为长方体的支点,则在长方体不倾倒(即长方体不倾斜脱离圆柱体)的情况下,根据力矩平衡,可得:
(1a)
(1b)
在水平方向上,由牛顿第二定律可得出长方体的运动方程为
(2)
长方体在运动过程中受到的空气阻力f与速度的平方成线性关系[6],因此有
(3)
其中,η=CρA/2,C为垂直平面体空气阻力系数,ρ为空气密度,A为长方体迎风横截面积.
对本文的模型来说,木板在往复运动中速度不断变化,2个圆柱相对匀速转动,不会发生无滑滚动的情况,同时不考虑形变所致的滚动摩擦,即只考虑滑动摩擦[7],则
fN=f1+f2=μ1N1+(-μ2N2),
(4)
其中,μ为滑动摩擦因数.
下面详细分析摩擦振子中长方体受到的滑动摩擦力fN. 一般情况下,可认为滑动摩擦因数μ是常量,但本文中滑动摩擦力是驱动长方体运动的关键量,且在实际情况下,滑动摩擦因数由于相对速度等的变化而改变,最终导致其具体表达式较为复杂. 受参考文献[8]的启发,假设长方体滑动摩擦因数与相对速度u之间具有线性关系:
μ=a+bu,
(5)
其中a和b为与物体表面性质有关的常量.
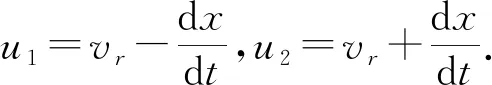
fN=μ1N1-μ2N2=
(6)
分别将(3)和(6)式代入(2)式,得到圆柱1、圆柱2分别按照顺-逆时针旋转情况下,长方体的运动状态方程为
(7)
1.2 圆柱1和圆柱2分别按照逆-顺时针旋转
此情形下长方体的运动过程与1.1情况不同之处只有摩擦力的方向发生改变,因此1.1情况中的(1)和(2)式以及长方体所受到的空气阻力(3)式在此情况下仍适用.
当圆柱1和圆柱2分别按照逆-顺时针旋转时,长方体受到的滑动摩擦力fN表达式为
fN=-μ1N1+μ2N2=
(8)
分别将(3)和(8)式代入(2)式,可得到当圆柱1和圆柱2分别按照逆-顺时针旋转时,长方体的运动方程为
(9)
2 实验探究
实验使用2个直径D=7.43 cm的圆柱,以及长度l=45.23 cm、宽度w=2.04 cm、厚度d=1.53 cm的长方体木条,组成摩擦振子系统.
2.1 测量圆柱与长方体之间的滑动摩擦因数
如图3所示,将两圆柱靠近并固定在一直线上,并用胶带固定圆柱使其无法转动. 再调节该直线与水平方向呈一定的角度θ,使长方体在圆柱上面自由滑落.

图3 测量滑动摩擦因数实验装置图
取木块运动的方向为z轴正向,根据简单的受力分析,可得到长方体下落的加速度为

(10)
由于圆柱被固定无法旋转,因此圆柱与长方体的相对速度即为长方体自身的速度,即u=dz/dt,结合(5)和(10)式,得出:
(11)
实验中,设置θ=30°,将长方体下落的过程拍摄视频,并利用Tracker软件逐帧分析视频,得到长方体质心随时间变化数据. 使用Matlab软件,利用(11)式对实验数据进行拟合,如图4所示,证明了(5)式假设的正确性. 同时,通过拟合实验数据,得到(5)式中与物体表面性质有关的常数值分别为a=0.266,b=-0.009.
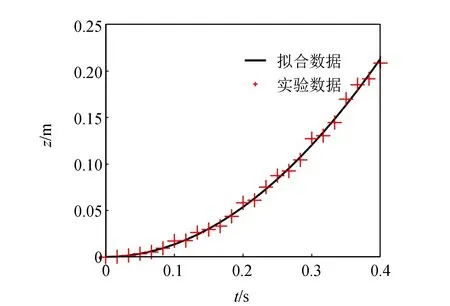
图4 下落过程中长方体质心的变化
2.2 分析实验条件下的空气阻力系数相关常量η
垂直平面体空气阻力系数可认为C≈1.0[9],空气密度为ρ≈1.3 kg/m3,长方体迎风面积为A=wd=3.12 cm2. 根据以上数据,计算得出η≈0.000 20.
2.3 圆柱1和圆柱2分别按不同方式旋转摩擦振子的质心变化
实验装置如图5所示,用绳索反向连接两圆柱,使两圆柱获得大小相等方向相反的角速度,用电机控制圆柱体的转速. 质量m=16.4 g的长方体放置于间距S=30.00 cm的两圆柱上,并设置圆柱体以ω=66.0 r/min旋转,从而驱使长方体运动. 此时,圆柱外围线速度为vr=ωD/2=0.257 m/s.

图5 摩擦振子实验装置示意图
对于圆柱1和圆柱2分别按照顺-逆时针旋转的情况,将长方体放置在两圆柱上,令x|t=0=4.00 cm,使圆柱开始旋转. 通过Tracker软件测量长方体质心随时间的变化情况,实验结果如图6所示. 实线是将上述各参量代入(7)式后得到的理论曲线.

图6 顺-逆时针旋转m=16.4 g时摩擦振子的质心变化
从图6中可以看出,长方体的运动轨迹近似为余弦曲线,但实际振幅在缓慢增大,即摩擦振子做振幅变化的往复振动. 从图6也可以看出,实验数据与理论分析得到的曲线基本吻合,证明了(7)式的正确性.
为了进一步证明上述理论分析的正确性,保持其他实验参量不变,仅改变长方体的质量为m=21.3 g,重复上述实验. 图7显示实验结果和理论曲线基本一致.
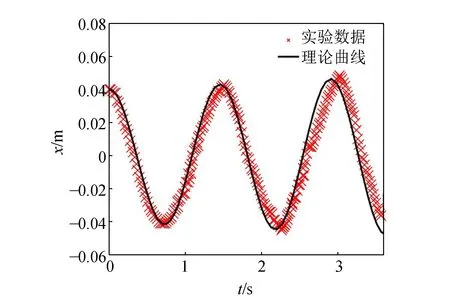
图7 顺-逆时针旋转m=21.3 g时摩擦振子的质心变化
选用m=16.4 g的长方体作为摩擦振子,在x|t=0=1.00 cm时,设置圆柱以ω=66.0 r/min开始旋转. 通过Tracker软件得到摩擦振子的质心随时间变化情况,结果如图8所示,实线是将上述已知参量代入(9)式后得到的理论曲线. 从图8中可以看出,实验数据与理论曲线吻合度较高,进一步证明了理论分析的正确性.

图8 逆-顺时针旋转m=16.4 g时摩擦振子的质心变化
同时,从图8中也可以看出,在圆柱1和圆柱2分别按照逆-顺时针旋转情况下,由于长方体运动过程中将不断远离两圆柱轴心位置,最终脱离圆柱系统,此时不存在振动现象. 本文重点研究的是摩擦振子现象,所以圆柱1和圆柱2分别按照逆-顺时针旋转这种情况将不再分析.
3 仿真模拟
上述实验结果已经证明了理论分析(7)式和(9)式的正确性. 当摩擦振子系统中某些参量变化时,长方体的运动状态也将随之改变. 受到当前实验条件的限制,采用控制变量法,基于理论结果对摩擦振子现象进行仿真模拟.
3.1 两圆柱轴线距离S发生变化时,摩擦振子的运动情况


图9 S取不同值摩擦振子的质心变化
从图9中可以看出,两圆柱轴间距S越大,则摩擦振子往复运动的周期就越大. 同时,随着运动时间的增加,两圆柱间距S越大,摩擦振子运动的振幅也越大.
3.2 长方体在具有不同滑动摩擦因数μ时的运动情况
由于μ中含有a和b参量,因此分析a和b单独变化时摩擦振子的运动情况.


图10 a取不同值摩擦振子的质心变化
在相同实验参量条件下,当固定a=0.266,仅改变b值时,根据(7)式可得到摩擦振子运动曲线如图11所示. 由图11可以看出,b值并不会影响摩擦振子运动的周期. 当b>0时,随着运动时间的增加,摩擦振子运动的振幅将迅速减少;当b<0时,随着运动时间的增加,摩擦振子运动的振幅将迅速增大;当b=0时,随着运动时间的增加,摩擦振子运动的振幅在短时间内基本保持不变,可认为长方体近似做简谐运动. 但是,即使b=0,随着运动时间的增加,实际上摩擦振子往复运动的振幅也将减小,仿真结果如图12所示. 这是由于空气阻力的存在,对摩擦振子运动造成了阻尼所致.

图11 b取不同值摩擦振子的质心变化
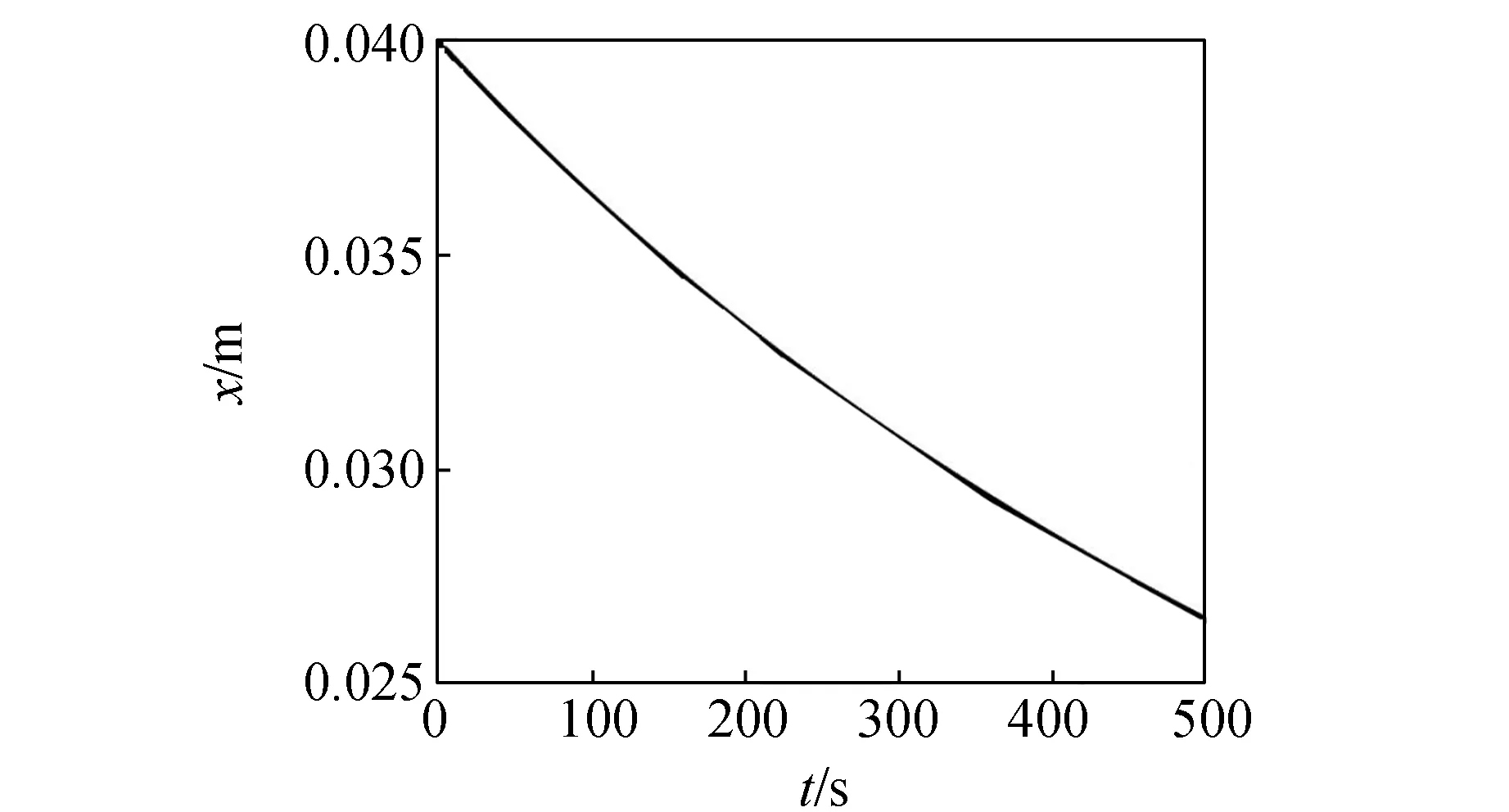
图12 b=0时,摩擦振子长时间运动质心的振幅变化
3.3 空气阻力系数η对摩擦振子运动的影响
保持上述各实验参量不变,仅改变(7)式中η的取值,摩擦振子的运动情况如图13所示. 从图13可以看出,空气阻力系数η的改变基本不影响摩擦振子的运动状态,即一般条件下的空气阻力对长方体运动的影响极其微小.

图13 η取不同值时摩擦振子的质心变化
3.4 当圆柱外围线速度vr变化时摩擦振子的运动
保持上述各实验参量不变,仅改变(7)式中vr的取值(即改变圆柱体运动的角速度ω),摩擦振子的运动情况如图14所示.
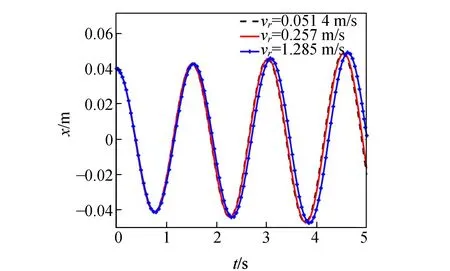
图14 vr取不同值时摩擦振子的质心变化
从图14可以看出,vr的微小变化对摩擦振子运动的影响较小. 但随着vr的大幅度增加,摩擦振子质心运动的周期将稍变长,且随着运动时间的增加,摩擦振子质心的运动振幅也将增大.
说明:本文的理论模型,假设长方体只在水平方向上运动,但在实际运动过程中,长方体在竖直方向有微小幅度的振动,这会导致其受到的支持力产生变化,进而造成实验结果和理论结果的微小偏差. 此外,实验数据通过Tracker软件获得,软件分析的精确度也会导致实验数据与理论分析之间存在偏差.
4 结束语
对第33届IYPT赛题中摩擦振子进行了理论和实验的研究. 建立了摩擦振子的运动模型,通过对摩擦振子的受力和运动状态分析,从理论上得出了当圆柱体分别按照顺-逆时针和逆-顺时针旋转时,摩擦振子的运动状态微分方程. 实验搭建了摩擦振子系统,并对理论分析结果进行了实验研究,实验结果和理论分析基本一致.
