基于贝叶斯融合与仿真的系统剩余寿命预测

宋兆理, 贾 祥, 郭 波, 程志君

(国防科技大学系统工程学院, 湖南 长沙 410073)

0 引 言

在工程实践中,复杂系统的可靠性和剩余寿命(remaining useful life,RUL)预测是重要的研究问题。尤其是对于大型工程,例如卫星研制与发射等,可靠的系统级RUL预测可以为上层决策提供强有力的支持,从而科学化地降低整个系统工程的运营成本,提高系统的可用性。

单个设备的RUL称为单机级RUL,而由多个单机或更多层级组成的复杂系统的RUL称为系统级RUL。对于处于工作状态的设备,无论是在单机层面还是在系统层面,都需要合适的RUL预测方法来监管设备的使用方式,制定将来的维护和更换计划。与单机级RUL相比,系统级的RUL预测往往更加重要,也更加困难。单机级RUL预测的关键在寿命分布、数据特征、融合策略等方面[1-2],而系统级的RUL预测还需要考虑系统结构、信息折算等[3-5]。因此,探索有效的系统级RUL预测方法是可靠性研究领域的重要问题之一。近年来已经涌现出一些研究成果,大致分为3大类:① 基于贝叶斯理论的方法;② 基于随机过程的方法;③ 统计学方法。

对于具有高可靠性和少量数据的设备,贝叶斯理论可以充分利用验前信息和试验数据。文献[6]提出一种贝叶斯非参数估计方法,以获取具有单机和系统验前的系统验后可靠性函数。基于贝叶斯框架,最小方差无偏估计器(minimum-variance unbiased estimator,MVUE)[7]或数据驱动的预测器[8]可以准确地进行系统状态估计。在典型的系统可靠性结构中,串联和并联结构的工作原理相对简单,因此基于贝叶斯理论的相关研究成果和公式推论较多[9-12];而对于表决系统和冷备系统,由于其结构的复杂性,简便易操作的方法较少。

对于设备使用过程中产生的性能监测数据,很多方法通过建立基于随机过程的可靠性模型进行系统级RUL预测。一定程度上来说,这些方法能够还原系统在工作状态下的真实退化过程,从而保证预测精度。目前,利用随机过程预测系统级RUL的模型很多,例如Markov过程[13]、Gamma过程[14]、Wiener过程[15]、Petri网[16]。文献[17]将系统视为一个整体考虑其性能退化过程,提出了一种基于解析模型的RUL预测方法。这些方法运用场景广泛,能够在无法获得失效数据的情况下预测系统的RUL,但数据来源相对单一,在预测对象具备多源信息的条件下,难以基于不同类型的信息进行融合预测。

统计学方法内涵丰富,包括非参数分析、回归分析、蒙特卡罗(Monte-Carlo,MC)仿真等一系列具体方法。文献[18-19]使用极大似然估计方法进行了卫星和卫星子系统的非参数可靠性分析和威布尔拟合。统计学方法对不确定性问题具有良好的鲁棒性,能够比较准确地预测系统RUL,所以被越来越多地用于随机疲劳分析和可靠性分析中[20-22]。然而,由于随机仿真预测的精确度是建立在足够的时间成本之上,所以难以满足工程中存在的实时预测的需求。

通常,系统级RUL预测往往趋于在单机级融合所有信息,然后通过系统结构将其转换到系统级,导致数据损耗。如果将融合过程推迟到系统级[23],则原始的单机级信息可以直接折合到系统,减少信息折损。因此,本文提出一种将贝叶斯融合和随机仿真相结合的方法,在系统级融合现场信息和单机提供的多源验前信息,进而预测系统的RUL。该方法既能借助贝叶斯理论将多源信息融合运用,又能发挥仿真方法便捷准确的优势,为系统级RUL预测提供一套完整可行的流程。

1 系统描述与假设

系统通常由具有特定结构的若干个单机组成,例如图1所示的卫星平台上的某功能系统。该系统可以分为3个子系统,分别由S1、S2和S3表示。具体地,S1子系统是包含5个C1单机的5中取3冷备结构;S2子系统是由3个C2单机,2个C3单机,1个C4单机和6个C6单机组成的混联结构;S3子系统是包含4个C5单机的2/4(G)表决结构。

图1 示例系统的可靠性框图Fig.1 Reliability block diagram of the prototype system

根据可靠性框图,可以通过逐层划分,将复杂的系统分解为具有特定关联形式的单机,从而呈现出系统的逻辑结构。

本问题聚焦于系统级的RUL预测,所以不考虑单机级的计算过程,而是基于所有单机的多源信息已知的前提构建模型。当任何单机的信息源存在少量缺失时,将利用易于获得的专家信息(如可靠度估计值、寿命估计值等)来填补这些丢失的数据。这样可以保证每个信息源都能获取到系统的无信息验前分布,并与系统级的试验信息相结合来预测RUL,从而避免该方法不适用于不完整信息的情况,增强其适用性。

威布尔分布通常被用于描述系统的故障过程,其概率密度函数(probability density function,PDF)、可靠性函数和累积概率分布函数(cumulative probability function,CDF)分别为

f(t)=λβtβ-1exp(-λtβ)

(1)

R(t)=exp(-λtβ)

(2)

F(t)=1-exp(-λtβ)

(3)

式中,λ和β为威布尔分布的参数。值得注意的是,当β=1时,即为指数分布。为了更好地描述预测模型,系统中信息源和单机的数量分别用n和m表示。在各个信息源和单机层面,用i(1≤i≤n)表示信息源的序号,用j(1≤j≤m)表示系统中单机的序号。在仿真中,用k表示根据单机寿命分布获得的样本量,l(1≤l≤k)表示单机寿命样本xi, j(l)的序号。

考虑到系统RUL预测的复杂性,本文建立的模型适当简化了实际问题,提出以下3个假设:① 系统的结构清晰,可以用可靠性框图来描述;② 系统中所有单机都是独立的;③ 除工作单机外,连接部件均完全可靠,如冷备系统中的开关等。

2 融合建模与预测

根据多源信息,可以通过单机级的寿命预测方法[1-2,24]获得与每个单机的不同信息源相关的寿命分布。本模型不考虑单机级的计算过程,将单机寿命分布作为预测模型的原始信息。此外,系统级还提供了少量的现场试验数据,其中包含被监测系统的寿命数据和工作状态。对于具有极少失效特征的高可靠性系统,极高的测试成本导致测试数量很少,所以现场试验信息是系统RUL预测的重要参考。

本文提出的RUL预测流程如图2所示,每种信息都可以独立计算,并基于贝叶斯理论在系统级融合来自每个信息源的验后分布,提高最终预测结果的准确性。应当注意的是,当可以确定单机的多源信息来自同一设备时,在贝叶斯估计中不需要进行一致性检验。

图2 系统级RUL预测流程Fig.2 Prediction procedure of system RUL

2.1 寿命样本随机仿真

对于每个信息源,已知单机寿命的CDF和PDF分别为Fi, j(t)和fi, j(t),其中i=1,2,…,n,j=1,2,…,m。借助反函数法和从0到1的随机数,可以通过仿真获得单机的寿命样本xi, j(l)(l=1,2,…,k)。具体的采样步骤如算法1所示。

算法 1抽取单机的寿命样本

步骤 1对于第j(j=1,2,…,m)个单机的第i(i=1,2,…,n)个信息源,在0～1之间生成连续均匀分布的k个随机数α,使Fi, j(t)=α,得到k个单机寿命样本。

步骤 2对于系统中的所有m个单机,重复步骤1,得到第i个信息源对应的所有单机的寿命样本。

步骤 3对于已知的所有n个信息源,重复步骤1和步骤2,得到每种信息源对应的所有单机的寿命样本{xi, j(l)}(i=1,2,…,n;j=1,2,…,m;l=1,2,…,k)。

接下来,需要借助这些寿命样本将单机级的信息传递到系统级。以4种常见的可靠性结构为例进行说明,用Yi,S、Yi,P、Yi,G和Yi,C分别表示串联结构、并联结构、表决结构和冷备结构的寿命样本集。实际上,这些传递原则不仅限于单机级,同样也适用于子系统级和系统级。

从仿真的角度来看,根据各个单元的寿命样本集合,串联结构、并联结构和r/m: G表决结构的系统寿命样本分别为

(4)

(5)

Yi,G(l)=xi,m-r+1(l)

(6)

式(6)中的单机寿命样本xi,m-r+1(l)来自将表决系统中所有样本升序排列后得到的样本集合{xi,1(l)≤xi,2(l)≤…≤xi,m(l)}。

在m中取r冷备结构,假设所有备件都相同,则每个位置的故障过程都是独立的[25]。对于任一部件位置,每当工作单机发生故障时,都会有一个冷备单机被激活,并接替其继续工作,从而延长了该部件位置的寿命。以此类推,当所有冷备单机都被激活后,一旦有单机发生故障,系统将停止工作。因此,使用寿命最短的部件位置决定了冷备系统的寿命。具体抽样过程如算法2所示。

算法 2抽取冷备系统的寿命样本

步骤 1对于第j(j=1,2,…,m)个单机的第i(i=1,2,…,n)个信息源,从冷备系统中的单机寿命样本{xi, j(l)}(l=1,2,…,k)中找到m个样本作为最开始工作的单机,记为CLi, j(l)=xi, j(l),已失效的单机数p=0。

步骤 2找到min CLi, j(l),令CLi, j(l)=CLi, j(l)+xi, j+1+p(l),更新p=p+1。

步骤 3重复步骤2(m-r)次,直到系统失效部件超过r个,得到系统寿命为Yi,G(l)=min CLi, j(l);

步骤 4重复步骤1～步骤3k次,得到冷备系统的寿命样本集Yi,C。

2.2 多源验前分布推导

根据单机级信息获得系统级不同信息源对应的寿命样本Si(1≤i≤n)后,采用贝叶斯方法将这些信息视为验前信息,与系统级信息融合进行RUL预测。在贝叶斯融合中,主要步骤包括将多源信息分类为验前信息和现场信息,由验前信息确定验前分布以及融合现场试验数据得出验后分布。

各个信息源的系统寿命样本集合可以近似描述寿命的分布特征,被视为系统的验前信息。同时,系统的已记录寿命数据被视为现场试验信息。以下是从一个信息源的角度进行分析计算的方法,不同信息源的过程是相同的。

通过对系统寿命样本进行排序,假设显著性水平为α,易得寿命的100(1-α)%置信区间为[QL,QH]。置信区间反映了寿命样本的分布,可以用来计算系统的验前分布,从而达到将单机级信息折合到系统级的效果。

为了根据不完全信息获得参数的验前分布,通常采用最大熵方法(maximum entropy method,MEM),其中信息熵可以作为目标函数[26]。显然,RUL的置信区间[μL,μH]满足Fτ(μL)=α/2和Fτ(μH)=1-α/2,其中Fτ(t)表示在τ时刻系统RUL的CDF。在系统寿命服从威布尔分布的情况下,置信区间的下限μL和上限μH分别为

(7)

根据MEM原理[27],约束问题可以表示为

(8)

(9)

由工程经验假设λ服从Gamma分布,β服从均匀分布,λ和β互相独立,则其融合验前分布为

(10)

式中,a和b是需要计算的超参数,λ∈[0,∞),β∈[βL,βH]。

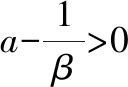
(11)

根据式(7)～式(11),可以通过

(12)

计算得到a和b。式中,M1和M2是惩罚因子,需要通过数值方法计算[27],且

(13)

2.3 融合验后分布推导

随着多源信息验前分布的获得,必须将单机传递的验前信息与系统的现场数据结合运用以减少不确定性。通常,多源信息的融合验前分布表示为

(14)

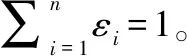
(15)

式中,

(16)

(17)

根据MLE-II原理,融合权重πi随L(D|πi)增加而增加,表示为

(18)

用P(D|λ,β)表示系统现场数据的似然函数,则系统的验后分布为

(19)

(20)

则融合验后分布可以表示为

(21)

式中,πi(λ,β|D)(i=1,2,…,n)是每个信息源的验后分布。不难发现,融合验后分布即为由多源验前分布获得的验后分布的加权总和。

根据贝叶斯理论,第i个验后分布可以表示为

(22)

对于一个寿命服从威布尔分布的系统,类似于式(15),现场试验数据的似然函数为

P(D|λ,β)=λgβgMβ-1e-λN

(23)

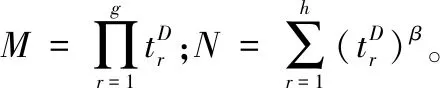
因此,第i个信息源的融合权重wi及其验后分布可以分别由式(20)、式(22)和式(23)得到,从而通过式(21)加权融合获得最终的验后分布。

2.4 系统RUL预测

根据式(1)～式(3),在获得参数验后分布的条件下,系统RUL的点估计[5]为

(24)

同时,由置信区间的满足条件可以获得系统RUL的置信区间下限μL和上限μH分别为

(25)

(26)

得到融合验后分布之后,由于其形式复杂无法直接求解,故采用MC仿真[22]近似计算,过程如算法3所示。

算法 3求解RUL预测结果

步骤 1根据融合验后分布π(λ(ε),β(ε)|D)抽样,得到ϑ组参数样本{λ(ε),β(ε)}(ε=1,2,…,ϑ)。

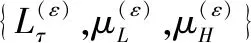
步骤 3对样本求均值作为系统RUL的无偏估计,得到预测结果。

3 实例验证

为进行方法验证,列举两个算例具体分析。算例1通过与仿真方法对比,验证了本文方法的正确性,算例2通过与现有方法对比,验证了本文方法的可行性。

3.1 算例1

本算例的系统结构如图1所示。根据工程实际问题提供的数据,在给定单机的相似产品寿命信息、历史寿命信息和性能监测信息3个信息源(n=3)的条件下,系统中6种单机的寿命服从不同的指数分布和威布尔分布。为了简化计算,本例认为来自相同单机的不同信息源提供相同的寿命分布。根据模型假设,单机的寿命分布相互独立。具体地,单机C1、C2、C3、C4、C5服从威布尔分布,单机C6服从指数分布,参数如表1所示。根据图2中的系统级RUL预测流程,给定来自多个信息源的单机寿命分布信息,每个分布生成k个样本。为分析k的不同取值对结果的影响,将k分别设置为1 000、2 000、5 000、10 000、20 000和50 000。然后,根据图1中的系统可靠性框图,可以将单机寿命信息折合为系统的验前信息,并获得系统样本集。

表1 单机的失效分布信息

根据工程经验,可以认为威布尔型系统形状参数的取值范围是2～10。单机级数据被视为系统的验前信息,该信息将通过参数模型结合系统级现场数据确定验后分布。给定的系统现场试验数据为不同时间开始工作的设备的定时截尾数据,分别是7 503 h、4 854 h、5 642 h、2 638 h、4 097 h,将其视为无失效数据。最终,当系统工作到τ时刻时,将获得参数的验后PDF,从而估计系统RUL。在本实例中,对于同一单机,由于不同的信息源来自相同的寿命分布,因此预测结果中每个信息源所占的权重几乎相等。

为了证明本文方法的有效性和可行性,将用仿真方法与其进行比较。在仿真中,不考虑多源信息融合,而是由表1中给出的信息直接提取样本,并将其按照第2.1节中的折算原则折合到系统级,从而作为验前信息计算RUL。仿真结果可以被认为是实际值,用作验证本文方法的参考。虽然本方法基于大量的仿真抽样,但算法的耗时都较小,以秒为单位,所以此例没有对算法的运行时间展开分析。表2汇总了两种方法在τ=2年时的RUL预测结果,包括点估计和80%置信区间,以及对应点估计的均方误差(mean square error,MSE)。图3展示了不同k取值情况下通过两种方法获得的PDF曲线。

表2 系统RUL预测结果

以仿真方法所得的系统RUL点估计预测结果为对比标准,本文方法所得点估计预测结果的相对误差如图4所示。

由表2可以看出,本文方法获得的系统RUL点估计和置信区间结果与仿真方法所得结果近似吻合,体现了本文方法的可行性。对于样本量k的不同取值,本文方法的MSE均小于仿真方法的MSE,说明本文提出的预测模型所得结果分布更集中,具有更好的收敛性。由图3可以看出,随着样本量k的增大,本文方法所得PDF曲线与仿真方法所得PDF曲线的重合度增加,反映了仿真实验“样本量越大,结果越精确”的特性。然而,当k不断增大时,仿真抽样的时间成本也不断提高,虽然本例的时间成本可忽略不计,但对于实际中的大型复杂系统来说,样本量的增大可能会使算法的运行时间成倍增长。因此,需要在保证结果精确性和较低时间成本的前提下,设置合适的样本量大小。通过分析图3和图4可以判断,当k=10 000时,预测结果已经基本稳定,且点估计预测的相对误差较低(小于5%)。

图3 不同k取值下本文方法与仿真方法所得的PDFFig.3 PDFs from the proposed method and simulation method with different k

图4 系统RUL点估计的相对预测误差Fig.4 Relative prediction error of system RUL point estimation

为了探究本文提出的RUL预测方法对于不同评估时期的适用性,在实例给定的τ=2年的前提下,将预测时间推迟,得到RUL点估计和置信区间的预测结果(设k=10 000)如图5所示。

图5 不同τ取值下系统RUL预测结果Fig.5 Prediction results of system RUL with different τ

由图5可以看出,系统RUL预测结果随着τ增大而减小,并且τ越大,τ与RUL预测值之和(即期望的系统寿命)越小。对于正常工作的设备,寿命期望值应维持不变,而此例中寿命随τ增大而减小,表明本方法对于工作到中后期的设备RUL预测趋于保守。这一现象与系统寿命服从威布尔分布的特性有关,其故障率会随着工作时间的延长而增大,导致系统加速退化,属于“浴盆曲线”的耗损故障阶段[29]。

3.2 算例2

本算例将本文中的预测方法应用于文献[30]中的实际问题(已省略时间单位),以验证本方法的可行性。该对比系统是一个简化的卫星系统,由7个单机组成,其结构如图6所示。

图6 对比系统的可靠性框图Fig.6 Reliability block diagram of comparison system

通过比较发现,利用文献[30]提供的系统和失效信息(见表3),及其寿命数据5.4, 8.59, 6.34, 6.08, 9.26, 5.11, 10.55, 6.37, 10.56, 4.73，可以应用本方法预测该卫星系统的RUL,并且预测结果与原方法所得的结果近似。另外,本方法还能预测RUL的置信区间,从而提供更丰富的评估结果。

表3 对比系统的失效信息

4 结 论

本文的问题来自工程实践中具有高可靠性和极少试验数据的卫星平台,在单机级RUL研究相对成熟的基础上,结合贝叶斯理论和随机仿真,提出融合多源信息的系统级RUL预测方法。当然,除了卫星平台系统,本文方法也适用于具有类似特征的其他系统。本文提出的方法具有较强的适应性,介绍的实例仅为验证提出方法的一种可能情况。在工程实践中,如果单机的寿命分布未知,可以通过性能退化监测来获得本文方法所需的寿命样本,同样能利用本方法进行系统RUL预测。本方法的优势还在于利用仿真将单机的失效信息传递到系统级,减少分析推导和计算的复杂操作;在系统级融合多源信息,减小信息折损,保证已知数据的充分运用;帮助决策者了解不同信息源在RUL预测中所占的权重,为后期的大型设备运行策略和任务规划提供支撑。

基于现有研究,后续将对更复杂的系统展开RUL分析,不局限于由独立单机组成的系统,深入考虑单机的相关性失效,以更贴近工程实际的应用需求。