改进最小二乘算法在天文定位中的应用

黄坤阳, 刘先一, 张志利

(1. 火箭军工程大学导弹工程学院, 陕西 西安 710025; 2. 中国人民解放军96901部队, 北京 100080)

0 引 言

运用数字天顶仪进行天文定位是一种高精度的天文定位方法,数字天顶仪通过电荷耦合元件(charge-coupled device,CCD)星敏感器拍摄星图,对拍摄的星图进行读取并与星表结合进行星图识别。建立识别恒星的CCD图像坐标系和天球切平面坐标系之间的映射关系,再迭代运算数次后最终实现对测站点位置的精确定位[1-7],其中坐标系转换参数的精度直接影响了最终的解算结果。

运用数字天顶仪定位时采用Helmet模型进行坐标之间的转换[8-12],恒星的CCD图像坐标和天球切平面坐标均含有一定的误差[13-18]。在对坐标转换参数进行解算时常采用最小二乘算法[19-22],最小二乘算法只考虑了观测量的误差,没有考虑系数矩阵的误差[23-25]。总体最小二乘算法能同时顾及系数矩阵和观测量的误差[26-28],但是总体最小二乘算法认为系数矩阵中的数值均含有一定的误差,实际上系数矩阵中存在着不含误差的常系数列(或常系数行)。

为了高精度地解算识别恒星的坐标转换参数,本文首先将最小二乘算法和总体最小二乘算法进行有效组合，构成混合最小二乘算法,既考虑了矩阵中的常系数列(或常系数行)也顾及了系数矩阵及观测量中的误差[29-32]。然后，针对数据中可能存在粗大误差的问题,考虑到混合最小二乘算法抵抗粗大误差的能力较差[33],提出稳健加权的混合最小二乘算法,对识别的恒星数据进行加权。最后，运用数据仿真对所提算法的优越性进行了证明。

1 天文定位中坐标转换模型

在运用数字天顶仪进行定位的过程中,由CCD星敏感器拍摄天顶上的星图,通过星表进行星图识别,建立识别恒星的天球切平面坐标系和CCD图像坐标系,两个坐标之间的转换采用Helmet转换模型,则有:

(1)

式中,(u,v)为识别恒星在天球上的切平面坐标,切平面坐标通过识别恒星的赤经赤纬解算得到;(x,y)为识别恒星的CCD图像坐标,通过读取CCD图像坐标得到;a,b,c1,c2为坐标转换参数。令

l=[u1，u2,…,un,v1,v2,…,vn]T

(2)

(3)

当识别星点的数目较多时,式(1)可表示为

l=Ax

(4)

式中,A为由识别恒星的CCD图像坐标组成的系数矩阵;l为切平面组成的矩阵;x为转换参数。

2 天文定位中坐标转换参数解算

2.1 最小二乘算法

当识别恒星点的数目多于求解参数的数目时,采用最小二乘算法求解参数。最小二乘算法考虑了观测量的误差,用V表示残差量构成的矩阵,则有:

V=Ax-l

(5)

运用最小二乘算法有:

VTP0V=min

(6)

(7)

运用最小二乘算法求解参数的前提是系数矩阵A中没有误差,但是在运用数字天顶仪进行定位的过程中,系数矩阵A由识别恒星的CCD图像坐标组成。在对图像坐标进行读取的过程中会产生一定的误差量,也就是采用最小二乘算法不能消除读取CCD图像星点时造成的误差,所以直接采用最小二乘算法是不合理的。

2.2 总体最小二乘算法

总体最小二乘算法是一种能够同时顾及系数矩阵和观测量误差的算法。在进行参数求解的过程中,当系数矩阵和观测量均含有一定的误差时,应当采用总体最小二乘算法。

结合式(4),当系数矩阵和观测量中均含有误差时,可将方程组表示为

(A+EA)x=l+El

(8)

(9)

式中,v1为识别恒星在天球切平面坐标中对应的误差;v2为识别恒星在CCD图像坐标中对应的误差。总体最小二乘算法估计的准则可表示为

(10)

在进行星图匹配时,可能因恒星质心误差或匹配错误等原因造成识别恒星数据中含有粗大误差,粗大误差的存在会直接影响参数最终的解算精度。而总体最小二乘算法对粗大误差的抵抗能力较差,所以直接采用总体最小二乘算法并不能有效消除粗大误差对参数的影响。

2.3 稳健加权的混合最小二乘算法

在进行天文定位的过程中,需要高精度地求解CCD图像坐标与天球切平面坐标之间的转换关系,而常用的坐标转换模型是Helmet模型。此时系数矩阵中含有不含误差的常数列,而其余每一列都有误差且不可忽略,并且在观测量中也含有一定的误差。

2.3.1 混合最小二乘算法

将最小二乘算法与总体最小二乘算法进行有效结合构成混合最小二乘算法,这样能够同时顾及到系数矩阵和观测向量的误差,并且能够考虑到系数矩阵中的常数列。

将系数矩阵A和转换参数x分解为

(11)

式中,m为观测量的个数;n为待估参数的个数;A1为不含误差的常数列;n1，n2分别为矩阵A1和A2对应的参数个数。可以将方程组表示为

A1x1+(A2+EA2)x2=l+El

(12)

采用奇异值分解法对式(12)进行求解,对系数A1进行奇异分解:

A1=QR1

(13)

将奇异分解得到的Q的转置矩阵QT左乘式(12)得

(14)

有矩阵:

(15)

所以可将式(12)分解表示为

(16)

(17)

式中,x2tls为运用最小二乘算法求解的结果。

然而在运用混合最小二乘算法求解模型参数时,没有将恒星数据中的粗大误差考虑在内,而粗大误差会对解算的参数产生较大影响,所以对混合最小二乘算法进行稳健加权处理。可得混合最小二乘算法残差值的表达式:

(18)

稳健混合最小二乘算法的参数估计值为

(19)

(20)

(21)

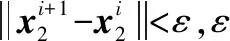
2.3.2 权阵P的设置

在天顶仪的拍摄过程中,由于城市灯光、空中飞行器、仪器电路噪声等因素的影响,星图中可能出现不存在的“假星”。同时,数字天顶仪采取离焦的方式拍摄恒星,星等越低,星点成像越大,灰度值越大。因此,恒星的星等越低,星点提取的精度越高,可靠性越好,加权时所赋权重应越大。数字天顶仪可观测的星等极限为11星等,天空中观测到的最亮恒星天狼星(大犬座α)为-1.45 Mv。Ii表示第i颗星的星等,Pi表示对应的权值,各星点的权值构成为

Pi=1-0.080 32×Ii

(22)

式中，Pi∈[0,1]。结合系数矩阵A的特点,设置相应权阵:

(23)

式中,P0的第1个和第2个对角元素为0,表示系数矩阵A的第1列和第2列不需要修正,其余对角线元素为1,表示矩阵A的第3列和第4列元素是等精度获取的;PX、PY与星等有关。

3 数据分析

在天文定位的解算过程中,识别恒星的天球切平面坐标和CCD图像坐标均含有误差,而且在恒星数据中可能会含有粗大误差。为了比较稳健加权的混合最小二乘算法对数据处理的效果,模拟出一组数据。构造函数u=-5x+8y+6,v=8x+5y+2,选取一组数据,如表1所示。

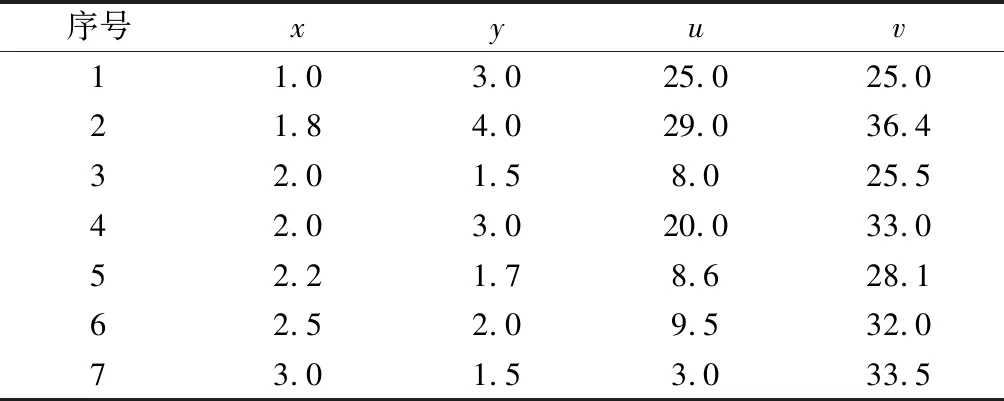
表1 初始数据值

对数据加入一定的误差,并在第4个数据上加入粗大误差,如表2所示。

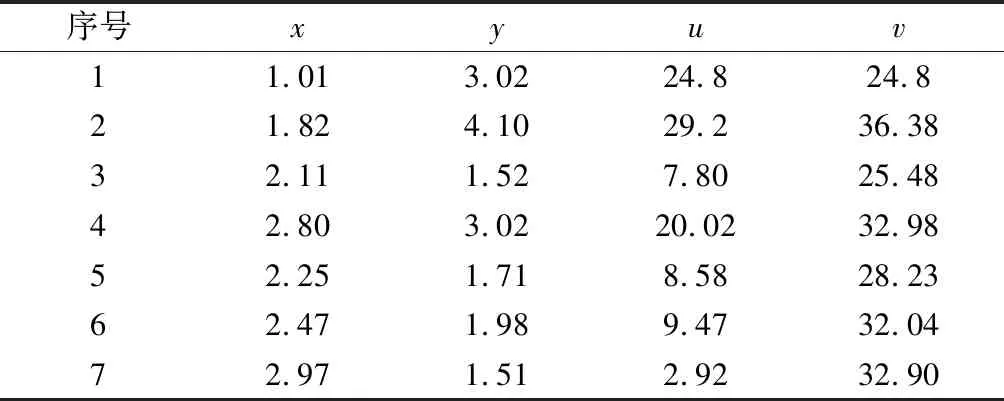
表2 添加误差的数据值

分别运用最小二乘、总体最小二乘、混合最小二乘和稳健加权混合最小二乘算法对系数求解,结果如表3所示。

表3 不同算法的求解值

对天文定位而言,天球切平面坐标系和CCD图像坐标系之间的转换系数会直接影响旋转中心的解算值,所以对坐标转换系数精度的要求就显得极为重要。以参数估计值与实际值之差的平方和作为评价解算方法优劣的一项重要指标,即

(24)

比较最小二乘、总体最小二乘、混合最小二乘和稳健加权混合最小二乘算法可以得出表4中的δ值。

表4 不同算法之间的比较值

从表4可以看出,不同算法的比较值差异较大。最小二乘和混合最小二乘的值比较接近,总体最小二乘的值最大并且远大于其他算法,稳健加权混合最小二乘的值最小。这表明运用稳健加权混合最小二乘解算的参数值与实际值最为接近,精度也最高。其他算法的精度从大到小依次为混合最小二乘、最小二乘和总体最小二乘，充分体现了稳健加权混合最小二乘算法的优势,证明了该算法能够有效提高天文定位中的求解精度。

4 结 论

运用数字天顶仪进行天文定位的过程中,坐标系转换参数的求解对于测站点位置的解算至关重要。本文对最小二乘算法和总体最小二乘算法进行有效组合，构成了混合最小二乘算法,并通过稳健加权消除粗大误差对解算结果的影响。通过对数据的分析,表明稳健加权的混合最小二乘算法在天文定位中的求解精度更高,解算的参数值与实际的值更为接近。