基于高斯混合模型的光纤罗经误差概率分布建模

胡耀金, 卞鸿巍, 王荣颖, 马 恒

(海军工程大学电气工程学院, 湖北 武汉 430033)

0 引 言

传统上认为船用罗经误差的概率密度分布基本符合正态分布,常常在正态分布的条件下分析罗经的误差性能特点,目前国军标中对船用罗经的性能测试就是以正态分布为前提的[1]。但通过多种数据统计分析方法对大量实际罗经误差数据概率密度特性进行分析,发现实际的光纤罗经误差的概率密度并不完全符合单峰的正态分布情况,而大多数呈现多峰特点,所以以往基于正态分布来分析罗经误差特性并不适用,影响对这一导航设备的性能评估、误差建模、特性分析以及设计补偿等工作,需要研究采用新的误差分布模型。

1894年生物学家卡尔·皮尔逊首先提出有限混合模型。由于有限混合模型的灵活性,其作为一种方便的、半参数的方法,广泛应用于信号处理[2-5]、电力系统[6-8]、导航制导控制[9-11]、机器视觉[12]、图像分割[13-14]等领域的复杂分布建模中。有限混合模型中最为常用的是高斯混合模型(Gaussian mixture model, GMM)[15-16]。通过使用足够多的高斯分布,并且调节其均值和方差以及线性组合系数,GMM能够以任意的精度近似逼近各种连续的概率密度分布[17]。

卡尔·皮尔逊最早使用矩方法(method of moments, MOM)来拟合具有不同均值和不同方差的两个正态分布的混合;自从期望最大化(expectation maximization,EM)算法出现以来,极大似然估计(maximum likelihood estimation, MLE)一直是拟合混合分布最常用的方法[15]。由于EM算法是一种数值迭代算法,EM解很大程度上依赖于其起始位置,有效的初始化是算法收敛到似然函数的最优局部极大值的重要前提[18-19]。EM初始化策略可以分为确定性策略和随机性策略[18]:确定性策略通常采用层次聚类或K均值聚类算法对数据集合进行聚类分析,将分析结果作为EM的初始值[20];随机性策略尝试使用不同的参数初始值,然后选择产生最大局部值的参数作为EM的初始值[21]。大部分初始化策略很难分出优劣,通常选择几种不同的策略,再从中选择似然值最高的一个。

对于GMM聚类数量的估计[22-23]可以分为两类:① 在似然函数的基础上添加对聚类的惩戒函数来反映其复杂度,构造新的EM目标优化函数,通过最大化EM目标函数得到最优的聚类数量,构造合适的惩戒函数是关键;② 基于信息论中最小化熵准则,例如赤池信息准则[24-25](Akaike information criterion,AIC)、贝叶斯信息准则[26-27](Bayes information criterion,BIC)等,这类方法以特定的准则测试模型来选择最优的聚类数量,缺点在于对组件数量变化不敏感,只有当组件数量变化超过10个,才能表明模型有明显的改进。

Yang等[28]提出了一种GMM的Robust-EM算法,该算法构建一种基于混合分布的新目标函数,然后创建新的EM算法更新方程。能够自动找到最佳聚类数量,通过将所有数据集合作为初始值来解决EM初始化问题。但没有考虑到数据集合具有重复数据情况,容易陷入到较差的局部最大值中。本文将基于该算法改进后对光纤罗经误差进行概率分布建模,从而对光纤罗经误差进一步分析。

1 GMM与EM算法

GMM满足如下形式的概率分布模型:

(1)

式中,αk是第k个高斯分布的混合系数,满足:

(2)

f(x;θk)是第k个高斯分布密度,θk包含均值向量μk和协方差矩阵Σk。假设观测数据x1,x2,…,xn由式(1)给出的GMM生成,对应的α和θ是需要估计的参数,通过最大化由式(3)给出对数似然函数来估计α和θ:

(3)

EM算法关键在于引入隐变量,将原问题分解。对于GMM引入隐变量zki,表示观测数据xi来自第k个分模型的数据是未知的,其定义如下:

zki=1:第i个观测来自第k个分模型;

zki=0:其他。

有了观测数据xi及未观测数据zki,完整数据是(xi,z1i,z2i,…,zki),对应完整的对数似然函数为

(4)

EM算法将原问题分解为两大步:期望步和最大化步。

期望步:用条件期望E(zki|xi;α,θ)来代替zki。根据贝叶斯理论得

(5)

(6)

最大化步:将式(5)的结果代入式(4)中得到式(6),最大化步是求式(6)对参数αk、μk和Σk的极大值。分别在式(2)的条件下求式(6)对αk、μk和Σk求偏导并令其为0,即可得到αk、μk和Σk的更新值:

(7)

(8)

(9)

不断重复期望步、最大化步直到收敛为止,即对数似然函数值不再有明显的变化。

2 Robust-EM算法

本节介绍了Yang提出的一种GMM的Robust-EM算法[28],在不确定聚类数量的情况下,能够有效地缓解对初始值的依赖,提高GMM对光纤罗经误差的概率分布拟合精度。

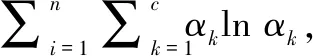
J(α,θ)=

(10)

式中,β≥0为惩戒系数。

将式(10)在式(2)的条件下对αk求极值,得到αk的更新:

(11)

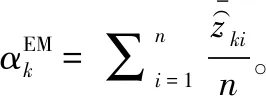
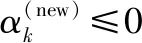
c(new)=c(old)-c(ill)

(12)

式中,c(ill)为不合理的聚类数量之和。

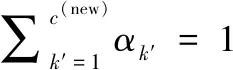
(13)

(14)

(15)

-e-1≤αklnαk<0

(16)

(17)

将式(16)和式(17)代入式(11)中得

(18)

从而有

(19)

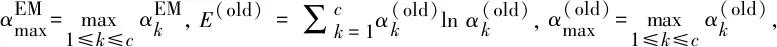
综合式(15)得到β更新式为

β=

(20)

在每次迭代过程,当聚类数量c达到稳定时,令β=0使得式(10)等于式(4),回归到传统的EM算法的迭代更新中。

在Robust-EM算法的初始化中,使用数据集合长度作为聚类数量初始c(initial)=n,对应的混合系数αk=1/c(initial);使用整个数据作为GMM均值初始值μk=xk。每个数据点与聚类中心的距离用向量的2-范数表示并对距离升序排序,其结果为

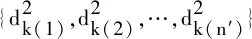
(21)

式中,sort{A}为对集合{A}进行升序排序。

(22)

式中,Id为d×d的单位矩阵。

在迭代更新Σk的过程中,由于c过大,αk过小,存在Σk奇异的问题,为避免这种问题,用约束协方差矩阵更新Σk,约束协方差矩阵表示为

(23)

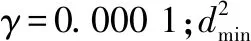
(24)

但Yang提出的Robust-EM算法存在问题:在实际的概率分布建模过程中,样本数据中存在很多相同的数据点,迭代更新时会生成多个参数相同的高斯分模型成分。Yang未将相同的高斯分模型成分进行合并,导致优化的目标函数陷入到较差的局部最大值,最终的拟合精度会大幅度下降。

因此,在Yang提出的Robust-EM算法基础上进行改进,即在每次的迭代更新后对相同的高斯分模型成分进行合并:统计每个模型参数,得到互不相同的参数和重复的频次,保持均值、协方差矩阵不变,混合系数和隐变量乘以重复的频次,再将改动后的参数代入下一次迭代过程。Robust-EM算法的伪代码如下。

算法 1Robust-EM算法

2 输出:GMM参数θbest

5 While 1 do

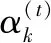
9 If(t≥60)&&(c(t-60)-c(t)=0)

10 令β=0

11 End

15 对相同的高斯分模型成分进行合并

17 Break;结束迭代更新

18 End

19t=t+1

End

3 仿真分析

设计一个三分量的一维GMM进行仿真分析,对比传统EM算法与Robust-EM算法的拟合效果。表1给出了该GMM真实参数与两者算法建立的模型参数。图1给出了对应的概率密度直方图。

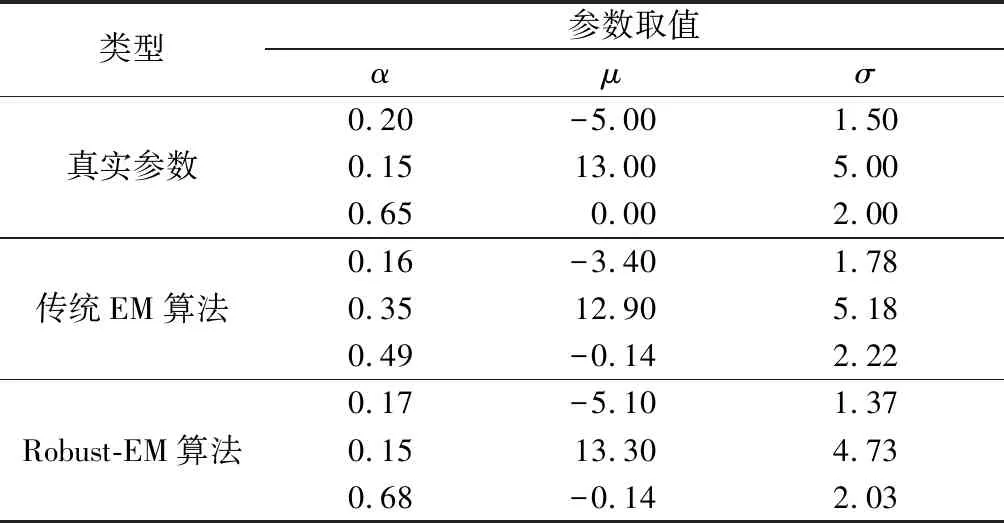
表1 GMM仿真分析参数

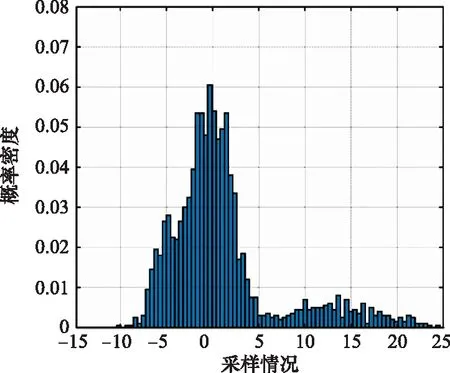
图1 样本数据概率密度直方图Fig.1 Probability density histogram of sample data

为了定量分析Robust-EM算法与传统EM算法的优劣,使用Kullback-Leibler divergence(简称为KL)[29]散度来比较两个算法建立统计模型之间的差异,真实分布p(x)和近似分布q(x)之间的KL散度表达式为

KL的值越小说明近似分布q(x)越接近于真实分布p(x),当KL=0时,q(x)=p(x)。

图2给出Robust-EM算法与传统EM算法的拟合效果,Robust-EM算法的KL=0.012 751,传统EM算法的KL=0.248 43。

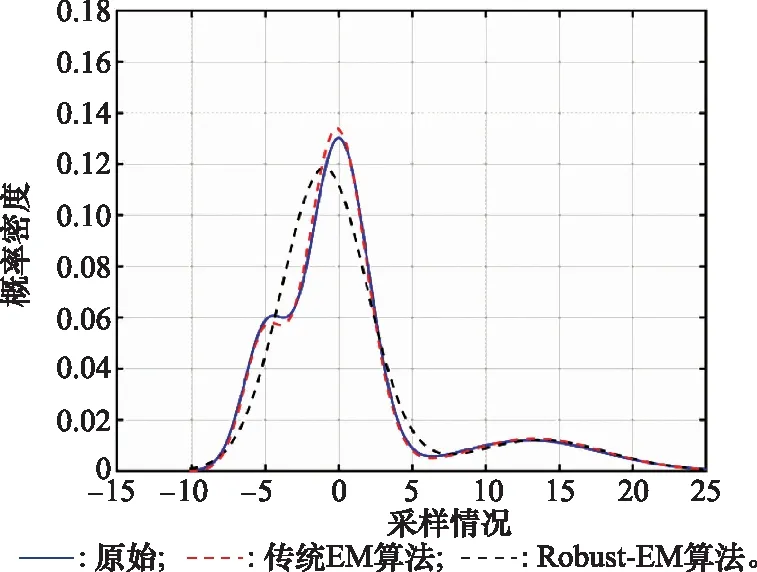
图2 Robust-EM算法与传统EM算法拟合效果Fig.2 Fitting effect of the Robust-EM algorithm and the traditional EM algorithm

从图2给出的结果和对应的KL散度可以得到Robust-EM算法明显优于传统EM算法。

4 实测数据分析

选取近年4套较为典型的新型光纤罗经作为试验设备,以实际的航向试验数据来验证GMM与Robust-EM算法在光纤罗经的误差建模上适用性。4套设备集中放置在试验船舶中。所有光纤罗经设备以计程仪辅助工作方式同时启动并连续工作20天,东西跨越14个经度,南北跨越7个纬度,数据采样频率为1 Hz;以高精度的GPS/SINS组合系统的航向值作为方位参考基准,所有采样数据进行了等比例降密处理。航行试验过程中机况、海况都很复杂,包括长距离航渡、直线、S形、O形航行状况,并遇到8级台风海况。

使用均方根误差(root mean square error, RMSE)作为指标来分析GMM对实际数据的拟合效果[30],RMSE越接近于0表明拟合效果越好,计算公式为

表2给出了各个GMM拟合的RMSE值。建模效果如图3所示,对应的GMM参数由表3～表6给出。

表2 设备GMM的RMSE

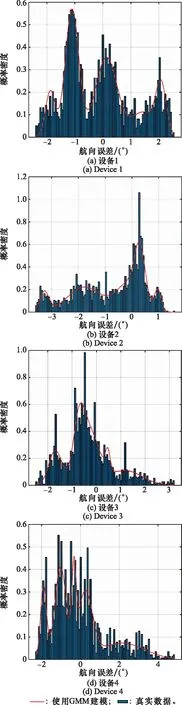
图3 GMM拟合效果图Fig.3 Fitting effect graph of GMM

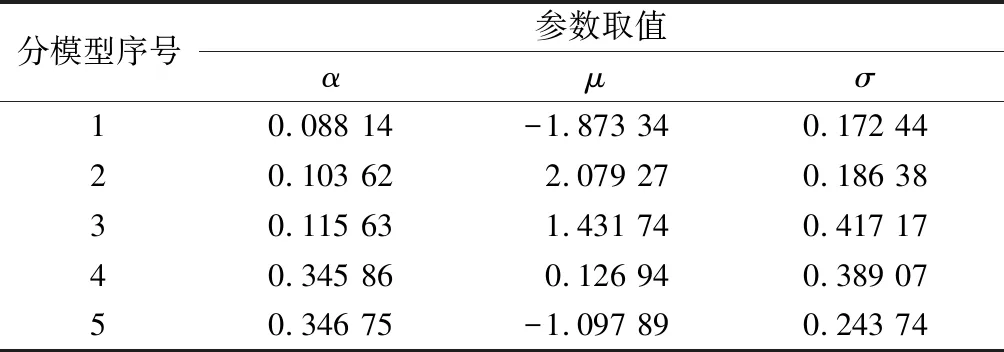
表3 设备1的GMM参数

表4 设备2的GMM参数

表5 设备3的GMM参数

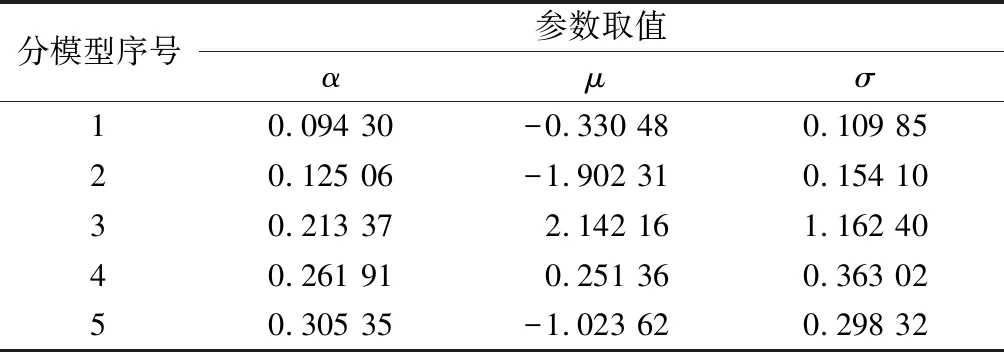
表6 设备4的GMM参数

综上分析,可以得出:

(1) 光纤罗经实际误差数据存在多峰现象是一种较为普遍的现象,且各设备多峰情况也不同,反映出光纤陀螺误差的复杂性和多样性。

(2) 本文采取的基于GMM的光纤罗经误差建模方法可以较好地解决多峰误差分布问题,并可以给出明确的模型参数。

(3) 基于RMSE的误差建模效果评估结果表明,全部设备样本误差建模结果均优于10%,最理想的样本结果优于5%,说明这一方法对于光纤罗经误差建模具有理想的拟合效果。

5 结 论

本文针对船用光纤罗经误差的概率分布不完全符合高斯分布的情况,通过对比传统EM算法和改进后的Robust-EM算法在GMM中参数估计的效果,验证了后者参数估计性能更为优异;将GMM与Robust-EM结合,对实际光纤罗经的航向误差数据进行概率建模分析表明,相比于只使用单峰的高斯分布,这一方法可以更加有效和准确反映其设备多峰误差的统计特性。这一方法对于其他导航设备的概率建模分析也有较好的推广意义,所建立的模型也可以应用于导航设备后续的性能评估、改进和误差补偿:对于罗经设计人员可以从误差模型找出设备的技术问题进行调整;对于测试人员可以根据误差模型完善试验方案,帮助论证更加准确的技术指标;对于组合导航设计人员,明确的概率误差模型可以应用到滤波信息融合。设备误差的概率分布与工况、海况密切相关,后续需要将航行轨迹分割为具有相同状况的子轨迹,分别对子轨迹进行建模分析,细致地分析设备误差特性。