基于标签多贝努利多传感器组网目标跟踪算法
2021-05-31杨超群
胡 琪, 杨超群
(中国电子科技集团公司第十四研究所, 江苏 南京 210000)
0 引 言
目标跟踪的本质是根据探测器获得的目标信息来估计目标的状态,包括目标起始、消亡、衍生、机动、监测区域目标个数等。目标状态估计的精度和稳定性不仅是整个探测系统的核心,也是评判探测系统最重要的指标之一。特别对于承担较大监测范围内或复杂电磁环境条件下的多目标跟踪任务的雷达,由于单个雷达的最大作用范围和波束资源有效,通常采用多个雷达组网的形式获取目标多全方位、多维度目标信息,以达到增大系统整体的探测距离、融合抗干扰、提高目标状态估计的精度和稳定性等目的。
多个雷达探测信息参与目标状态估计属于多传感器融合目标跟踪的范畴。多传感器融合根据处理架构的不同大体上分为3种形式,分别为集中式融合,分布式融合和混合式融合。其中集中式融合因其目标信息损失小、贝叶斯建模融合框架构建简单、工程实现简单等优点备受国内外学者关注。此外,对于目标点迹级融合来说,需要把所有传感器获得的目标点迹传送到融合中心进行处理,天然地适用于集中式融合的框架。点迹级集中式融合框架下的目标跟踪算法大多是单传感器目标跟踪算法扩展到多目标跟踪算法。例如,将最近邻(nearest neighbor, NN)算法推广到集中式多传感器NN(centralized multi-sensor NN, CMS-NN)[1-3];将全局NN算法引申到集中式多传感器全局NN(centralized multi-sensor global NN, CMS-GNN)[4];概率数据关联(probabilistic data association,PDA)算法被改造适用于多传感器目标跟踪环境[5-6];多假设跟踪(multiple hypothesis tracking,MHT)算法也被成功运用到多传感器系统中[7-8]。然而,上述算法理论上均不能解决数目变化的多目标跟踪建模问题,因此引入随机有限集(random finite set,RFS)思想来描述多目标跟踪场景[9-15]。同样地,RFS框架下的单传感器多目标跟踪问题也被尝试运用到多传感器场景中。概率假设密度(probability hypothesis density,PHD)框架分别运用迭代修正和多项乘积的思想提出了多传感器迭代修正PHD(iterated corrector PHD, IC-PHD)滤波算法[16-19]和乘积形式的多传感器PHD (product multi-sensor PHD, PM-CPHD)滤波算法[20-23]。此外,标签多贝努利(labelled multi-Bernoulli,LMB)框架[24-25]也初步探索应用于多个传感器数据级融合,提出了多传感器广义LMB(multi-sensor generalized LMB, MS-GLMB)算法[26-30]。基于RFS理论的算法最大优势在于能对探测区域内目标数进行建模并实时给出估计,然而上述RFS框架算法均假设目标同时落入多个雷达的探测范围内,即无法有效叠加不同探测器探测距离,导致目标数估计出现偏差。
本文针对数目变化的不同探测距离的多传感器组网目标跟踪问题,提出了一种基于LMB框架的多传感器组网目标跟踪算法。该算法将每个传感器的威利范围引入到目标建模中,得到适用于不同探测距离多传感器组网MS-GLMB(different detection range MS-GLMB,DDR-MS-GLMB)算法。仿真结果表明,该算法能有效叠加不同探测距离的多部雷达,使得多部雷达组网系统的探测范围得到有效叠加,不仅能稳定地获取有效范围内的目标状态,还能捕捉目标新生、消亡等关键时间,实时地给出准确的目标数估计。
本文的具体章节安排如下,引言部分给出了基础多传感器组网目标跟踪算法的研究背景和研究意义。第1节简单介绍了相关的RFS理论。第2节详细阐述了DDR-MS-GLMB推导过程和算法基本处理流程。最后给出了仿真分析性能对比和结论。
1 基于标签RFS目标跟踪算法研究现状
1.1 GLMB
Vo提出的GLMB滤波算法将目标的状态和标签空间相融合,是基于RFS理论的全贝叶斯跟踪器。不同于PHD、CPHD等滤波器只对状态进行建模,GLMB还对目标身份属性设置静态标签,即
Xk={xk,1,xk,2,…,xk,Nk}∈F(X×Lk)
(1)
式中,RFS集合Xk表示k时刻所包含的所有目标状态;带标签的目标状态向量具体形式为xk,Nk=(xk,lk)∈X×Lk;F表示带标签的目标状态向量的状态空间;xk和X分别表示不带标签的目标状态值和相应的状态空间;lk和Lk分别表示目标静态标签和相应的标签空间,静态标签lk=(k,i)中k表示目标的新生时刻,而i表示k时刻新生多个目标的序号。标签的构造能保证不同目标之间具有不同的标签,标签在整个滤波过程中动态分配给不同目标,目标标签一旦被给定,则在该目标的整个生存时间内不再改变。此外,标签随机集滤波一些通用符号如下:
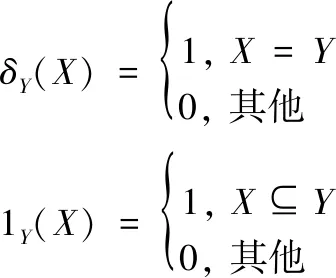
(2)
(3)
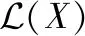
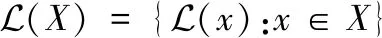
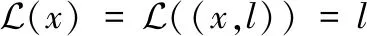
根据随机集积分规则[22],集合X中多个目标状态相对实数函数h的集积分可以简化为一个指数形式函数hX=∏x∈Xh(x),如果集合为空,则hφ=1。两个函数的内积可以表示为

1.2 MS-GLMB
MS-GLMB传感器的贝叶斯框架建模为
(4)
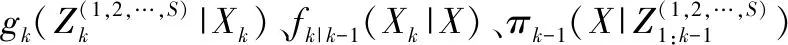
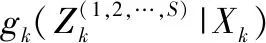
(5)
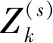
给定上一时刻后验概率密度函数和当前时刻的量测似然函数,基于式(4)中贝叶斯滤波框架得到当前时刻滤波后的概率密度函数形式为
πk(X)=
(6)
Θ=Θ(1)×Θ(2)×…×Θ(S),
θ=(θ(1),θ(2),…,θ(S))∈Θ
(7)
(8)

(9)

(10)
lBk(l)pB,k(·,l)
(11)
(12)
式中,下标+表示映射θ(s)(·)θ(s)(·)≥0中的情况;I+表示滤波后所有存活目标的标签集合;I表示滤波前所有可能目标的标签集合。值得注意的是,式(6)和式(4)具有相同的形式,表明整个滤波过程满足贝叶斯估计共轭先验的基本要求。
2 DDR-MS-GLMB滤波算法
基于LMB多传感器滤波算法需要在多个传感器中找到每个目标对应的量测(存在漏检、虚警等情况),然后再统一计算所有量测分配情况的似然情况。这就意味着算法建模伊始即假设目标都落在每个传感器的探测范围内,如式(10)所示。如若目标不在探测威力范围内,则找不到对应传感器的量测,该传感器的量测分配情况则一直是漏检,会影响整个量测分配情况似然权值的计算,继而影响目标状态估计和监测区域目标数估计情况。因此,必须把目标是否在探测威力范围这一重要因素纳入到似然权值的计算中。
仍然假设有S个传感器,每个传感器的自身位置和探测范围分别为(ST(j),DT(j)),j=1,2,…,S,目标i是否在传感器探测范围内可用如下公式表示:
(13)
式(13)表明,如果目标i存在于传感器j的探测范围内,则indi, j为1,否则为0。对于m个目标S个传感器可建立传感器指示矩阵:
IM(m,S)=
(14)
式中,i=1,2,…,m。
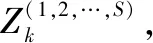
(15)
(16)
式中,第一种情况表明目标存活(包括目标漏检或目标量测更新),第二种情况表明目标消亡。
若直接从矩阵γ中寻找使权值(见式(15))最大的分配情况,则难免遇到非确定多项式问题。为此,可以基于矩阵γ构建多目标后验状态采样分布,用采样的方法来避免高维矩阵最优化问题。首先,对矩阵γ中的P个目标定义P个元,即
(17)
式(17)中4种情况的定义域分别为
(1) 1≤i≤R,(j(1),j(2),…,j(S))任意数小于0;
(2) 1≤i≤R,(j(1),j(2),…,j(S))全部大于或等于0;
(3)R+1≤i≤P,(j(1),j(2),…,j(S))任意数小于0;
(4)R+1≤i≤P,(j(1),j(2),…,j(S))全部大于或等于0。
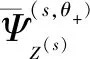

(18)
若当前目标不在某一个传感器探测范围内,理论上该传感器就不会采集到包含该目标的量测。在原始的MS-GLMB算法中,若该传感器一直无法获得该目标量测,会判定该目标在当前传感器一直处于漏检测的状态,造成目标计算出的权值偏小,最终导致传感器较难快速发现目标。特别是当组网范围内存在多个目标时,这种权值计算结果与实际情况不匹配的情况尤为严重。当一目标处在较多传感器探测威力交叉的范围内时,该目标权值较大。而当目标只处在一个传感器探测范围时,该目标的权值相对于多个传感器探测到目标显得更小,导致较难被Gibbs采样获取到,因此需要更多的样本才能解决该问题,但这会造成更重的计算负担。
本文利用前面得到的传感器指示矩阵,将目标相对于每个传感器范围的情况带入到该权值计算公式,即若目标(·,l)超出传感器的探测范围,则

(19)
若目标不在目标的探测范围内,该权值为1,相当于不纳入该传感器对该目标的影响,随后提供给Gibbs采样器权值所代表的目标量测空间概率分配更为合理,最终滤波器得到的结果也更为准确。
根据式(17)中定义的元,式(6)中目标后验概率分布可重写为
(20)
(21)
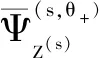
(22)
式中,γi代表第i个目标j(1),j(2),…,j(S)值的选取情况。
直接从式(20)的概率分布中采样是很困难的,需要基于该概率分布来构建合适的马尔可夫链使采样过程快速收敛到正确值[27]。一般情况下,可以遵循以下马尔可夫链的构建形式,即
πk(γ′|γ)=
(23)
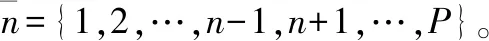

输入: γ(1),T,P,S,ηi=ηi((j(1),j(2),…,j(S))),i=1,2,…,P,|Z(s)|,s=1,2,…,Sm:=[-1;…,:-1];p:=ηi(γi)for (j(1),j(2),…,j(S))=(0,…,0):(|Z(1))|,|Z(2))|,…,|Z(S)|) m:=[m;[j(1),j(2),…,j(S)]]; end for t=2:T γ′k=[ ]; for n=1:P for(j(1),j(2),…,j(S))=(0,…,0):(|Z(1))|,|Z(2))|,…,|Z(S)|)pn(j(1),j(2),…,j(S)):=ηn(j(1),j(2),…,j(S)) ∏Ss=1(1-1{1:|Z(s)|}(j(s))1{γ′1:n-1,γt-1n+1:P}(j(s))) end γ′n~Categorical(m,pο); γ′k+1:=[γ′ο,k+1;γ′ο,n] end γ(t)=γ′k; End输出: γ(1),γ(2),…,γ(T)
其中,T表示采样器需要采样样本的个数,|Z(s)|表示传感器s量测集合的元素个数。
3 实验仿真
为了验证所提DDR-MS-GLMB滤波器的有效性,设计如下仿真场景:设置5个传感器不同站址的布局以及检测区域内存在多个数目变化的目标,5个传感器的位置分别为
S1=[-280 519,137 705]T
S2=[109 091,275 410]T
S3=[140 260,0]T
S4=[-265 935,-59 016]T
S5=[-46 753,-334 426]T
其中,每个传感器检测目标的概率均设为0.6,传感器笛卡尔坐标系位置的单位为m,每个传感器的有效半径均为40 km。每个传感器的虚警率设置为极坐标环境下每5°和每50 m的区域内为0.1%(每个传感器监测区域内每时刻产生杂波个数的泊松期望值大约为58),传感器的采样周期为5 s,每个传感器的周期误差为随机的0.1~0.3 s。具体情况如图1所示。
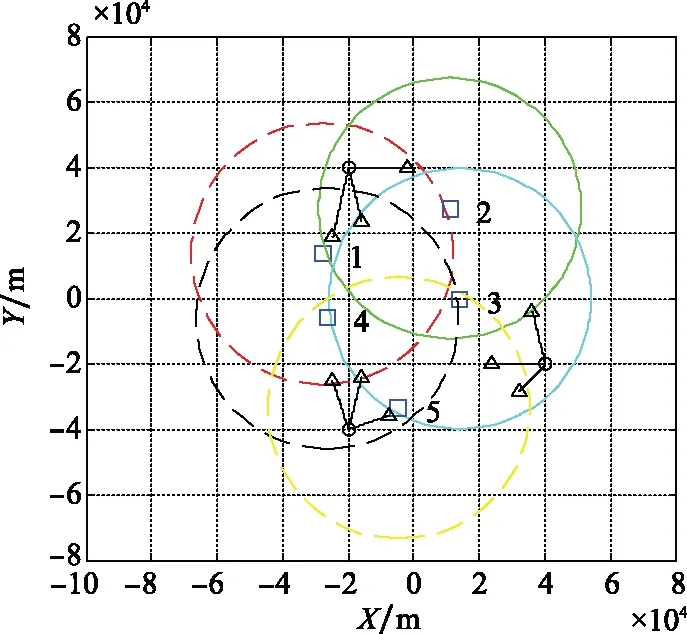
图1 目标真实轨迹、站址分布及各自威力范围Fig.1 Target real track, station location distribution and their respective power range
9个目标的出发时间和位置设置如下所示。
m1=[-20 000,8,-40 000,32]T,ts=1,te=100
m2=[-40 000,-8,-20 000,32]T,ts=10,te=110
m3=[-20 000,8,40 000,-32]T,ts=20,te=120
m4=[-20 000,-10,-40 000,30]T,ts=30,te=130
m5=[-20 000,-10,-40 000,30]T,ts=40,te=140
m6=[40 000,-32,-20 000,0T,ts=50,te=150
m7=[40 000,-16,-20 000,-16]T,ts=60,te=160
m8=[-20 000,35,40 000,30]T,ts=70,te=170
m9=[-20 000,-8,40 000,-35]T,ts=80,te=200
仿真实验结果如图2和图3所示。从图2中可以看出,本文提出的DDR-MS-GLMB算法能准确估计目标的个数,这得益于该算法实时计算目标是否在传感器的威力范围内,准确建模目标是漏检还是超出探测范围,据此来动态调整目标权值的计算方式,更能反应真实情况。而原始的MS-GLMB算法由于开始假设所有目标落在传感器探测范围内,目标只有漏检和消亡两种情况,无法准确计算目标权值,最终导致目标严重漏估。图3中MS-GLMB算法最优次模式(optimal sub-pattern assignment, OSPA)距离偏大主要是目标数估计不准造成的。

图2 目标数估计结果Fig.2 Target number estimation results
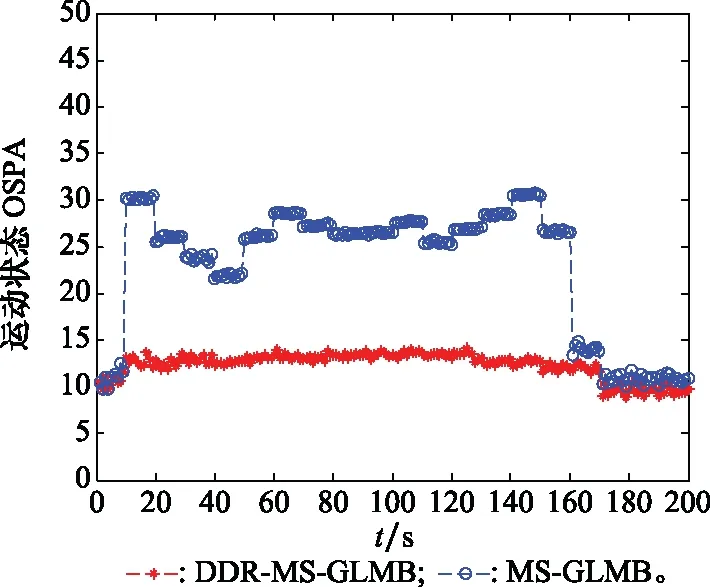
图3 OSPA估计结果Fig.3 OSPA estimation results
4 结 论
本文立足于实际多传感器组网场景,深入讨论了MS-GLMB算法工程应用问题。本文提出的算法将不同传感器布站以及传感器不同探测范围对目标跟踪的影响考虑到MS_GLMB算法建模中,提出了DDR-MS-GLMB算法,较好地将LMB多传感器框架应用于工程实际场景。实验仿真结果表明,所提算法能准确估计监测区域内目标数以及每个目标的状态。
