“分部积分法”的“钉钉子精神”课程思政教学探究

冯永平 邓明香

（广州大学数学与信息科学学院 广东广州 510006）

一、案例主题引入

数学分析主要利用极限工具研究各类函数的分析性质，如单变量函数的连续性、可积性与可微性，多变量函数的连续性、可微性与可积性等内容，是数学类专业、部分理工类专业的专业必修课程。其中不定积分是函数可积性中一个非常重要的教学内容，见[1，2]。不定积分运算是函数求导（微分）运算的逆运算，一般讲，正面运算（导数运算）由于有很多的导数求导法则，计算相对简单，而逆运算，是“找”原函数的过程，重点在于“找”，在于“构造”，如何去“找”或者“构造”没有统一的准则与模式，相对讲困难许多。

不定积分计算中常见的方法有基本积分公式、换元积分方法、分部积分方法[3]。基本积分方法简言之就是将基本导数（微分）公式反过来使用，也叫做“公式法”，基本积分方法只能计算非常简单函数的原函数，略微复杂函数的不定积分计算“公式法”是无法完成的。换元积分方法是通过凑微分方法或变量代换方法将看似复杂的积分简单化。分部积分方法是将“函数乘积的导数运算公式”逆用，通过被积函数的特殊选择与分解，简化复杂积分的计算。不定积分由于没有统一的准则与模式，很多初学者对如何计算不定积分有一种畏惧心理，不知如何出发去“找”或“构造”函数。

课程思政是新时代高校思想政治工作的一场深刻革命。习近平总书记强调，高校思想政治工作关系高校培养什么样的人、如何培养人以及为谁培养人这个根本问题。要坚持把立德树人作为中心环节，把思想政治工作贯穿教育教学全过程，实现全程育人、全方位育人，努力开创我国高等教育事业发展新局面。要把立德树人融入教育各环节，贯穿基础教育、职业教育、高等教育各领域。习近平强调，我们办中国特色社会主义教育，就是要理直气壮开好思政课，用新时代中国特色社会主义思想铸魂育人，引导学生增强中国特色社会主义道路自信、理论自信、制度自信、文化自信，厚植爱国主义情怀，把爱国情、强国志、报国行自觉融入坚持和发展中国特色社会主义事业、建设社会主义现代化强国、实现中华民族伟大复兴的奋斗之中。2017年5月，“课程思政”被纳入中央《关于深化教育体制机制改革的意见》，从地方实践探索转化为国家战略部署。2017年6月，教育部在上海召开高校思想政治理论课教学质量年上海调研片会暨高校“课程思政”现场推进会。2019年7月，“广东省教育厅关于强化课程思政建设一流课程的意见（粤教高【2019】7号）”为广东省高校课程思政建设拟定了指导性文件。

专业课程教学中融入思政元素是每位老师践行“立德树人”教育目标的基本要求，如何更好地展开课程思政，有很多专家已进行了初步的探索与实践[4，5]。“钉钉子精神”是习近平总书记以朴素的话语，提出的一个意蕴深远的命题[6]。做事好比钉钉子，是要找准方向一锤一锤接着敲，才能把钉子钉实钉牢。在2018-2019第一学期数学分析课程教学中，2019-2010第一学期微积分课程教学中，将“分部积分方法计算不定积分”与“钉钉子精神”类比教学，学生通过类比学习更易掌握计算不定积分的方法，更深刻理解了“钉钉子”精神，深刻把握了学习的主题，隐性地对学生进行了人生观与科学方法论教育。

教学中通过隐性地将“钉钉子精神”融入到教学中，通过对比，让学生更易处理“不定积分”计算中出现的困难与问题。

二、与专业教学内容相结合的思政融入点

通过长时间教学探索与实践，发现不定积分计算过程与习总书记倡导的“钉钉子精神”高度吻合。将“换元积分方法”与“钉钉子精神”相比较，加深同学们对分部积分方法的理解与应用。在讲述的过程中每一个环节与钉钉子相比较，让同学们更易掌握抽象的“分部积分方法”，通过浅显的道理对学生进行了人生观和世界观教育。

课程开始环节首先回顾了一些简单函数的积分方法，如公式方法和换元积分方法，主要思想是利用链式法则及反函数求导法则，将一些看起来复杂的积分通过变量代换转换为简单的积分。但在实际计算中经常碰到各种不同类型函数的乘积或某单一函数高次幂不定积分的计算，显然“换元方法”一般是很难处理这类“复杂积分的计算”。

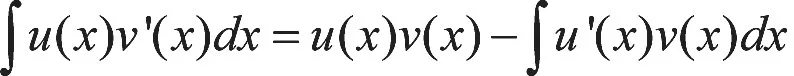
内容 思政融入点 教学过程和教学方法1。在哪里钉？（基础与环境）钉钉子做什么？(初心与使命)2。准备合适的钉子与锤子(材料与工具)3。如何定一颗钉子？3。1 看准钉子的方向（钉子要扶正、稳）；3。2 一锤一锤稳扎稳打；每锤落下应仔细观察方向有没有偏移？(工作中的敬业精神)；3。3 若钉了几锤没有进展，说明下面的环境不能钉钉子，换一个位置；教学过程和教学方法1。已经掌握了许多类型函数的积分（已经有了基础），一些较复杂函数的积分如images/BZ_191_1879_2382_1996_2434.png不定积分的计算（分部积分方法）怎么算？(初心与使命)2。找相应的公式与算法（分部积分公式），(方法与技术)3。 如何运用公式计算一个不定积分？3。1 计算不定积分有几个基本出发点，选择“适当函数”运用公式（无理化有理；高次化低次；函数类型归一化）；3。2 一步一步仔细计算、思考；每一步计算仔细后比较积分的难度有没有降低？（学习中要一丝不苟、严谨求实）；images/BZ_191_1581_2669_1962_2759.pngimages/BZ_191_1581_2765_1915_2854.png，II比I简单了。3。3 计算的过程中发现将积分更复杂化了，马上转换思路，换一种选择（方法总比困难多）；images/BZ_191_1581_2944_2069_3044.pngimages/BZ_191_1581_3049_2007_3148.png积分IV比积分III复杂多了,转换思路。

?

在课程讲授环节，让同学们回忆一下第一次“钉钉子”的经历，发现学生有很多的经验分享，多数同学对自己第一次钉钉子时的感受进行了分享，让同学们畅所欲言，从这件小事我们能总结出什么样的人生哲理呢？ 从中引出了计算不定积分其实与“钉钉子”过程是高度吻合的，引出了“分部积分方法”的思政教学过程。对典型或一些比较困难的不定积分计算，运用类比教学方法，同学们更易掌握“分部积分方法”的思想与过程，类比过程如上表。

紧接着通过类比，讲解了几种典型函数的不定积分过程，最后总结了运用分部积分方法计算不定积分的注意点。

通过实际生活案例的分享与讨论，将其隐性融入了数学专业课程课堂教学，“随风潜入夜、润物细无声”，专业课程思政应该起到这样的效果，也更容易让同学们领会贯通。

三、案例意义

结合自身的10多年教学经验和对数学学科的深刻认识，我们从“认识和传播数学文化”、“诱发对数学之美的探索”、“数学家的家国情怀”、“阐释数学哲学与人生价值”等多个方面讨论如何做到“知识传授与价值引领相结合”的有效路径。通过总结，我们归纳出的高等数学“立德树人”教学内容为：培养严谨求实态度，崇尚理性科学精神，提升数学自然审美，传扬真挚家国情怀。

在教学中，将看似简单的“钉钉子精神”与“计算不定积分”相比照，一方面将抽象问题通俗化，便于学生理解。在教学过程中，通过大家熟悉的“钉钉子”小事，让大家分享了各自的第一次经历，以此为切入点，类比讲述了“不定积分”的计算过程。更重要的是在教学过程中通过类比与小故事分享让同学们树立了正确的人生观（要牢记初心与使命，每一阶段要有目标和方向，做事要稳扎稳打循序渐进，工作要深入钻研不要做表面工作）与科学方法论（多角度看问题，条条大道通罗马（有难有易），积少成多，熟能生巧（千里之行始于足下））。

四、教学反思

通过教学实践，学生更易理解并运用分部积分方法，对在计算积分中碰到的困难与问题有了相应的处理思路。由于课时、课室限制，很难长时间、大面积展开。通过网络教学、线上教学或微课教学，让每个学生理解小故事中蕴含的大道理，让大多数同学对抽象的数学有更大的兴趣。