非一致曲率表面下的气压砂轮磨粒剪胀及加工试验研究
2021-05-27计时鸣黄鹏程郑倩倩
石 梦 李 卓 曾 晰 计时鸣 黄鹏程 郑倩倩
1.浙江工业大学特种装备制造与先进加工技术教育部重点实验室,杭州,3100232.金华职业技术学院机电工程学院,金华,321017 3.浙江中烟工业有限责任公司杭州卷烟厂,杭州,310024
0 引言
在传统模具光整行业中,模具型腔表面60%以上都是曲面,其中40%为自由曲面,而模具的凹面和凸面处的材料去除和抛光效果不均匀[1],且表面具有高硬度的特点,这些使得模具表面抛光自动化程度低[2]。研究高效、精密、自动化的非一致曲率模具表面光整技术,对模具行业发展具有重要意义。
在现有的柔性光整加工方法中,英国光学实验室与Zeeko公司提出一种气囊抛光技术[3-5],并应用于回转对称型器件的表面抛光加工。宋剑锋等[6]研究了气囊抛光的材料去除特性,致力于提高光学元件的形面精度。以上加工方法在加工过程中磨粒均处于游离状态,以滚动的姿态对工件进行微力切削,材料去除能力较弱,难以对高硬度表面进行高效光整。计时鸣等[7]提出了软固结磨粒气压砂轮抛光新方法,在砂轮内部通入一定压力的气体,并绕一定倾角的回转轴做回转切削运动,砂轮的柔性仿形能力使得该方法适用于具有非一致曲率的加工对象。
为实现对非一致曲率表面的可重复性、确定性抛光,对材料去除量进行定量的建模和分析显得非常重要。软固结磨粒气压砂轮内部的磨粒相互离散,组成离散颗粒体系,剪胀效应是离散颗粒体系的基本特性[8-9]。计时鸣等[10]研究了气压砂轮加工过程中磨粒群内部发生的剪胀效应,并建立了磨粒群内部的微观接触力学模型。目前部分学者将抛光过程中接触区的抛光环境视为均匀接触问题,并基于Preston方程来研究抛光过程中的材料去除量,忽视了曲率变化引起抛光接触区内应力分布不均问题[11]。
本文研究了软固结磨粒群内部剪胀效应,以颗粒接触理论建立磨粒黏结层的力学模型;结合层状力学分析软固结磨粒气压砂轮的加工力学模型,并且从细观角度分析了在工件不同曲率半径的接触区内的应力分布以及磨粒的速度分布规律;对经典的Preston方程进行修正,建立材料去除方程;通过颗粒流仿真软件EDEM模拟分析了软固结磨粒气压砂轮在不同曲率表面下的接触力与速度分布规律。最后搭建机器人抛光试验平台,研究非一致曲率表面下软固结磨粒气压砂轮加工方法的材料去除量以及工件的表面质量。
1 非一致曲率下的磨粒剪胀与材料去除模型
软固结气压砂轮作为一种新型的抛光工具,其内部通入一定压力的气体,外部由磨粒黏结层与橡胶基体层构成双层体系结构,具有良好的仿形能力。图1所示为气压砂轮结构。

图1 软固结磨粒气压砂轮抛光图Fig.1 Polishing diagram of SCA pneumaticgrinding wheel
在抛光试验中砂轮能较大程度地拟合工件的接触表面形貌,在脱离抛光接触区域后,在砂轮空腔充气压力的作用下砂轮能迅速恢复原貌。在砂轮抛光非一致曲率表面时,曲率的变化使得砂轮在接触区内产生不同的形变,导致接触区内磨粒群发生不同程度的剪胀效应。另一方面抛光表面曲率的变化也引起了磨粒群速度发生相应变化。
1.1 非一致曲率下砂轮层状力学模型
磨粒黏结层中的磨粒在黏结剂作用下,黏结成一种密实排列的颗粒集群。在宏观上,随着砂轮的转动,各磨粒的运动状态保持一致;在微观上,由于抛光过程外力的变化,磨粒群中的磨粒相互挤压、接触,磨粒相互位置发生改变,磨粒群内部发生的主要是体积膨胀效应,磨粒间孔隙被增大,从而发生了体积变化,这种现象被称为剪胀,如图2所示。
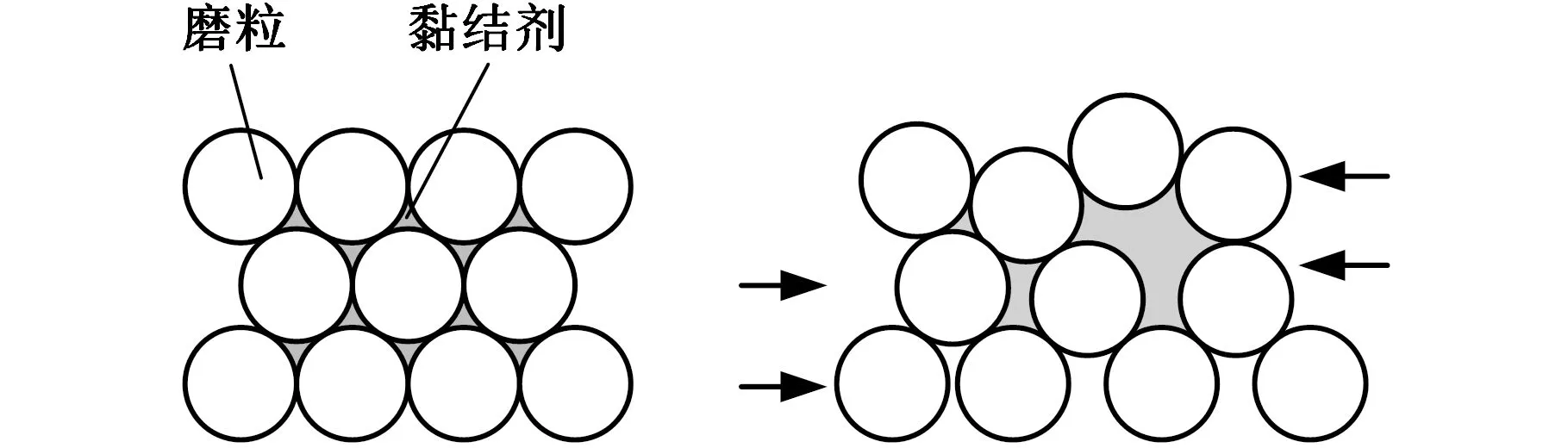
图2 软固结磨粒群剪胀示意图Fig.2 Schematic diagram of dilatancy of SCA
ROWE[12]基于纯粹的摩擦变形机制和最低能量比的假设,并利用剑桥模型得出了直线形剪胀方程。在软固结磨粒气压砂轮抛光试验中,由于砂轮的转轴与平面有一定的倾角,造成磨粒剪切过程中应力、应变出现共轴的现象。基于Rowe剪胀方程,引入非共轴系数c,得到修正的Rowe剪胀方程:
(1)
式中,dR为剪胀系数;Mr为临界状态线的斜率(或者相位转换点对应的应力比);q为偏应力;c与当前应力状态应变分量有关;dεv,p为塑性体变增量;dεq,p为塑性剪应变增量;Sij为偏应力张量分量;εij,p为塑性应变张量分量;p为有效平均主应力; 下标p表示在有效平均主应力为p的情况下各变化量对应的值。
磨粒群在发生剪胀的过程中,其变形的主要影响因素为磨粒间的法向接触力以及表面黏附能。该气压砂轮中的磨粒粒径为微米尺度,其表面积与体积的比值很大,表面效应尤为明显。JOHNSON等[13]考虑接触物体的表面黏附能对接触半径的影响提出了JKR模型。使用该模型描述黏结层中磨粒接触时的法向应力状态,可得两颗粒相对位移与所受有效平均主应力p之间的关系:
(2)
p1=p+3πΔγr′+[6πΔγpr′+(3πΔγr′)2]1/2
式中,dδ为两磨粒间的相对位移;Δγ为黏附能;r1、r2、E1、E2、υ1、υ2分别为两颗粒的半径、弹性模量和泊松比。
软固结磨粒气压砂轮抛光时,切削力的另一个重要影响因素为橡胶基体层的力学性能[14]。软固结磨粒群的切削力主要源于砂轮内部充气压力P,为研究软固结磨粒的切削力学模型,建立软固结磨粒气压砂轮的切削力学模型,基于砂轮的双层弹性结构进行力学分析。图3所示为砂轮的双层结构模型。
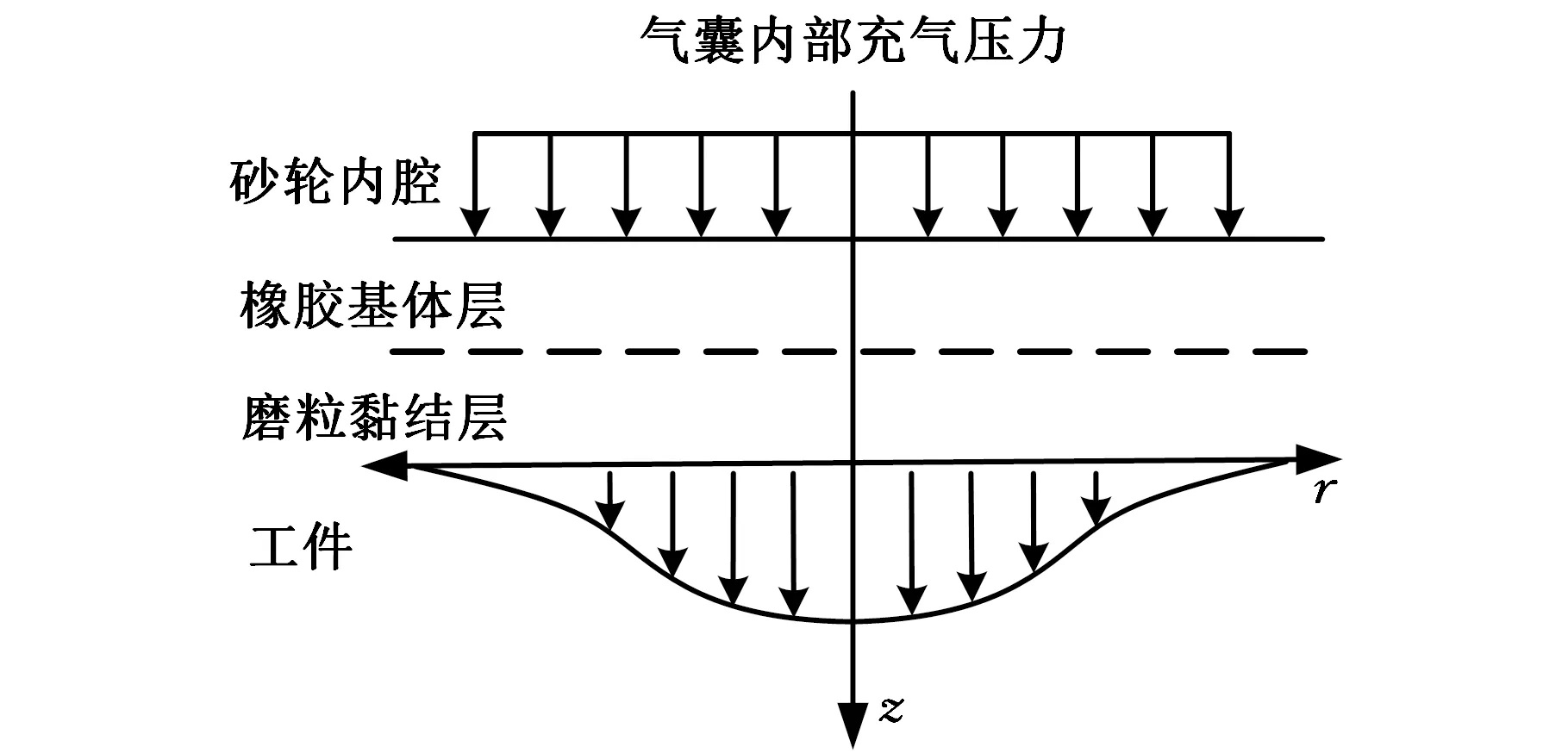
图3 气压砂轮层状力学体系Fig.3 Layered mechanical system of pneumaticgrinding wheel
在加工过程中,砂轮磨粒黏结层和橡胶基体层在边界层需拥有相同的行为约束,磨粒黏结层在加工时才不出现脱落现象。基于层间结合处完全连续条件可得
σz1=σz2
(3)
式中,σz1、σz2分别为磨粒黏结层与橡胶基体层接触处的正应力分量。
非一致曲率表面在抛光过程中,因气压砂轮具有一定的柔性,故与工件接触形成的抛光区会受接触区所属工件上的曲率影响。将工件表面分成凹面、平面、凸面三种情况展开讨论。在既定的下压量情况下,分析三种曲率表面下砂轮与工件形成接触区的面积情况,如图4所示。
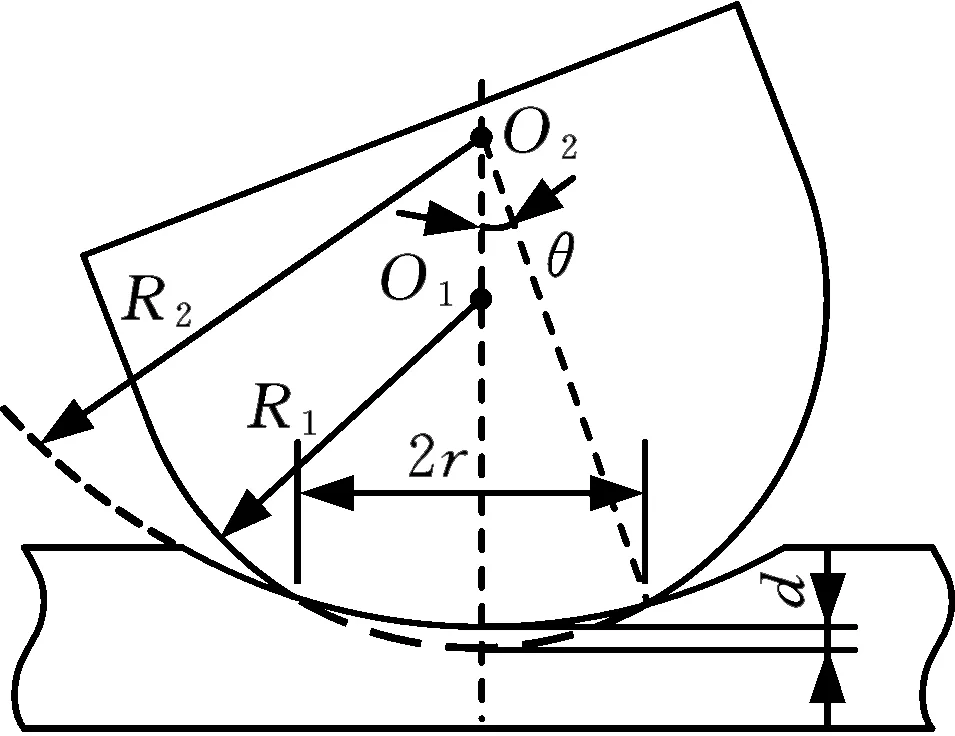
(a)凹面等效接触面
砂轮与凹面、平面、凸面工件接触形成的等效面积A的表达式如下:
(4)
式中,d为砂轮下压量;θ为工件凹面曲率中心与接触区边缘角度;R1为砂轮半径;R2为工件接触区曲率半径。
在软固结磨粒气压砂轮加工非一致曲率表面时,砂轮的下压量较小,砂轮与工件的接触区可近似视为圆形区域。在该圆形接触区域内,使用高斯分布的统计学模型对接触区处砂轮外层形变特征进行描述[15],即该圆形接触区域内砂轮外层在沿半径方向上的压缩量与接触中心的距离服从正态分布,可得抛光接触区内的接触力模型:
(5)
式中,h为圆形接触区内不同位置的下压变量;φ(h)为服从均值为d、方差为σ2的正态分布,φ(h)~N(d,σ2);εV为剪胀引起的体积变化;d2为弹性层形变量。
1.2 非一致曲率下的抛光接触区速度场分析
软固结磨粒气压砂轮的磨粒黏结层对接触区处的工件表面实现拟合,砂轮沿一定的倾角做匀速回转运动。在接触区处,磨粒黏结层受压变形,造成内部的磨粒速度发生改变。在接触区内的磨粒速度分布不均,如图5所示,砂轮与工件表面接触时接触处的切向平面为L2,砂轮中心与接触区中心连线所在的且平行于接触区中心速度方向的平面为L1,以两平面相交线上的速度作为接触区磨粒平均速度。如图6所示,以该磨粒的运动轨迹长度L与砂轮做回转运动转过β角的时间t的比值作为接触区磨粒的平均速度。接触区磨粒的平均速度
(6)
式中,β为接触区弦长与砂轮中心轴线垂直平面对应的圆心角;ω为砂轮角速度。

图5 砂轮与工件形成的切平面与速度平面Fig.5 Cutting plane and velocity plane formed bygrinding wheel and workpiece
1.3 非一致曲率表面下的材料去除模型
基于以上对软固结磨粒气压砂轮的抛光接触区的接触力与速度的分析,通过修正的Preston方程来描述材料去除量[16-17],其方程可以表示为
(7)
式中,M为材料去除量;K′为修正系数。
2 非一致曲率下的软固结气压砂轮加工数值模拟
2.1 接触模型参数设置
分析上述非一致曲率表面下的软固结磨粒气压砂轮材料去除模型可得,不同的接触区曲率会影响抛光时接触力的大小以及速度分布情况。为了验证理论模型的正确性,对非一致曲率表面下的软固结磨粒气压砂轮的接触力与速度变化进行数值模拟。使用EDEM颗粒流仿真软件建立砂轮模型,导入UG三维绘图所建的工件模型。图7所示为凸面工件的仿真模型。

(a)凹面接触区速度
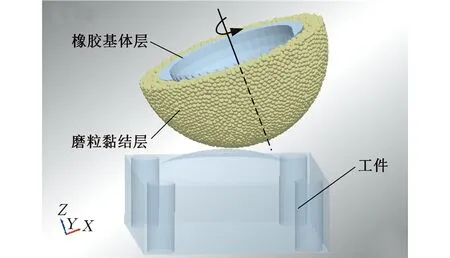
图7 凸面接触下的仿真模型Fig.7 Simulation model under convex contact
考虑磨粒群中各磨粒之间存在切向与法向的位移,采用Hertz-Mindlin with Bonding模型进行接触力与磨粒速度仿真。模型参数如表1所示。
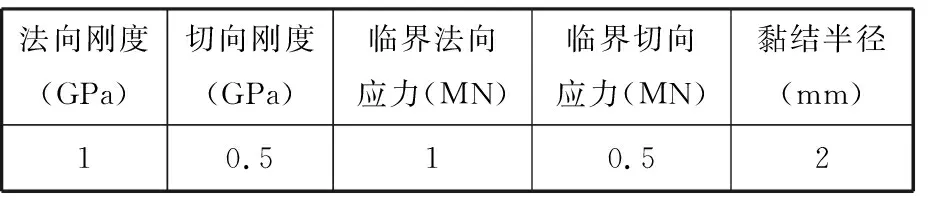
表1 Hertz-Mindlin with Bonding模型参数
EDEM中建立的砂轮模型参数如表2所示。为研究不同曲率半径下的气压砂轮加工特性,分别按照上述参数,通过改变接触面曲率,分析三种不同曲率情况下的受力与速度。

表2 软固结磨粒气压砂轮参数
2.2 非一致曲率表面下接触区的切削力模拟
气压砂轮磨粒黏结层的磨粒排布密集,形成颗粒集群。当加工接触区为不同曲率时,颗粒之间形成的黏结作用将砂轮内部充气的力传递至抛光接触区。工件曲率参数如表3所示。图8显示
了对应表3中不同曲率条件下的软固结磨粒群接触力网。
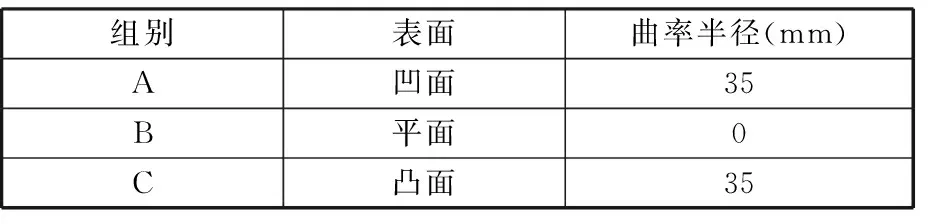
表3 工件参数
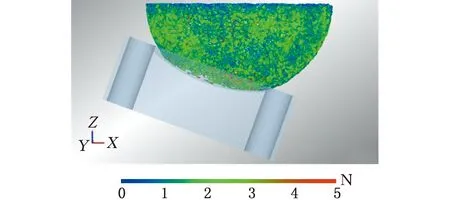
(a)A组磨粒接触力网
通过设置不同的接触面曲率,模拟非一致曲率表面下的抛光试验。在磨粒接触力的传递过程中,磨粒发生不同程度的剪胀效应,导致磨粒之间的接触力大小不同。从以上仿真结果可以看出:凹面接触时,磨粒之间形成的接触力最大,并且在全局上保持一定的均匀性;平面和凸面接触时,由于砂轮与工件表面接触,砂轮表面形变量较凹面大,砂轮的转动导致砂轮内部颗粒接触力分布有一定的差异。
砂轮与工件接触区的接触力大小与颗粒间的接触力有紧密联系。上述三组仿真试验中,工件接触区的接触力曲线见图9。从图9中可以看出,曲率不同,砂轮与工件形成的有效接触区面积不同,导致砂轮抛光接触力不同。对抛光试验中砂轮的运动过程进行分析,砂轮以一定的初速度接触工件并达到设定的下压量。在这个过程中,砂轮受外力作用,内部磨粒发生剪胀效应,使得试验中接触力F快速增大。在达到预定下压量后,砂轮以一定的转速旋转,最终与工件接触的砂轮局部处受力达到一种动态稳定。达到动态稳定状态后,凹面的接触力最大,平面次之,凸面最小。

图9 软固结磨粒接触力仿真曲线Fig.9 Simulation curve of contact force of SCA
根据砂轮在表3所示的三组不同曲率表面下的接触力仿真结果,取达到动态平衡时数据的平均值与式(5)的理论计算值作比较,结果如表4所示。

表4 抛光接触力对照表
由表4可知,仿真值要略小于理论值,这是因为在加工过程中,磨粒群中磨粒发生蠕动造成相对速度的改变。最终的计算误差在6%以内,理论模型基本可以使用。
2.3 非一致曲率表面下接触区的速度场模拟
根据2.1节中的模型参数设置,得到三组不同曲率条件下的抛光接触区速度图,见图10。

(a)A组磨粒速度图(b)A组接触区内磨粒速度图
如图11所示,将三组数值模拟的接触区磨粒速度均值与式(6)得到的计算值做比较。从图10与图11中可以得出软固结磨粒气压砂轮在不同工件曲率条件下的速度场规律:①在软固结磨粒气压砂轮旋转条件下,底部存在速度接近于0的区域。若直接以砂轮旋转轴垂直于加工面的方式进行抛光试验,不仅速度很小影响抛光过程中的材料去除效率,而且会造成接触区磨粒速度方向变化程度过大,不利于形成高质量加工面。在抛光试验中可采取一定的砂轮倾角来避免这个问题。②在三种曲率的接触面条件下,凸面与凹面的接触区平均速度均大于平面接触区的平均速度,与1.2节中建立的接触区速度模型保持一致。砂轮在接触工件表面后,砂轮的柔性使得砂轮外层沿着接触区运动。在磨粒刚进入接触区时,由于速度方向存在一定程度上的突变,其中凸面的颗粒速度变化程度最大,平面次之,凹面与砂轮的拟合情况最好,它在刚进入接触区时速度虽然有变化,但是变化程度较小。③三种接触条件下,由于砂轮中黏结剂的作用,每颗磨粒均受到良好的弹性支撑,使得接触区磨粒速度在整体上保持了较好的一致性,为获得高质量的加工表面提供了保证。

图11 磨粒速度理论值与仿真值对比图Fig.11 Comparison between theoretical value andsimulation value of abrasive velocity
本节将接触面分为凹面、平面、凸面三类进行仿真比较,证实了气压砂轮磨粒层中的剪胀效应,得到了接触力在不同工件表面曲率下的变化规律。接触区曲率与砂轮曲率的拟合程度越高,在砂轮达到动态平衡后,抛光接触力越大。分析三种曲率条件下抛光接触区域的速度场发现:在磨粒群随砂轮转动与工件形成的接触区内,沿着接触区内磨粒群速度方向,在开始接触处,磨粒群速度发生了不同程度的突变,随着砂轮的转动,接触区速度场趋于平稳,且磨粒运动方向保持有良好的一致性。
3 试验与讨论
3.1 软固结磨粒群的构成
考虑到软固结磨粒气压砂轮在抛光时,内部磨粒的相对位置时刻改变引起剪胀,在制备气压砂轮时,需要选择合适的磨粒材料与黏结剂种类[18]。棕刚玉磨粒硬度适中、颗粒锐利且成本低,适合加工抗张强度高的材料,因此在砂轮的制作过程中,磨粒材料选择为棕刚玉。同时,内部磨粒需要良好的弹性支撑,并且在抛光过程中产生的热量要求黏结剂具有良好的耐热性。酸性硅酮胶对磨粒有很好的黏合性,并且能与橡胶基体层结合完整,因此选用酸性硅酮胶为磨粒黏结剂。图12所示为制作好的砂轮头。

图12 砂轮头Fig.12 Wheel head
3.2 非一致曲率加工表面对切削力的影响
为了验证非一致曲率表面对砂轮加工中切削力的影响,首先对软固结磨粒气压砂轮在光整试验中的接触力进行测量。以表3中三种曲率的工件为测试对象,研究曲率对切削力大小的影响。图13所示为不同曲率的三种工件。

(a)凹面工件 (b)平面工件 (c)凸面工件图13 三组工件图Fig.13 Three sets of workpiece diagrams
图14所示为软固结磨粒气压砂轮光整试验平台,该平台以日本安川公司生产的Montoman-HP20机械臂为运动主体实现加工过程的位姿和轨迹控制,砂轮由直流电驱动,内部由空气压缩机通入0.01 MPa的气体,提供抛光时的主要切削力。根据表5的试验参数,在机器人抛光平台上安装三维力传感器J-K3D120-200N,分别对三组曲率表面下的工件接触力进行测定,测定结果如图15所示。

图14 机器人抛光平台Fig.14 Robot polishing platform

表5 抛光试验参数设计
由图15可以发现,试验所得接触力的趋势与接触力仿真结果基本一致。对比式(5)与接触力试验值可得:凸面理论值误差为4.9%,平面误差为7.3%,凸面误差为3.2%,计算误差小于10%,
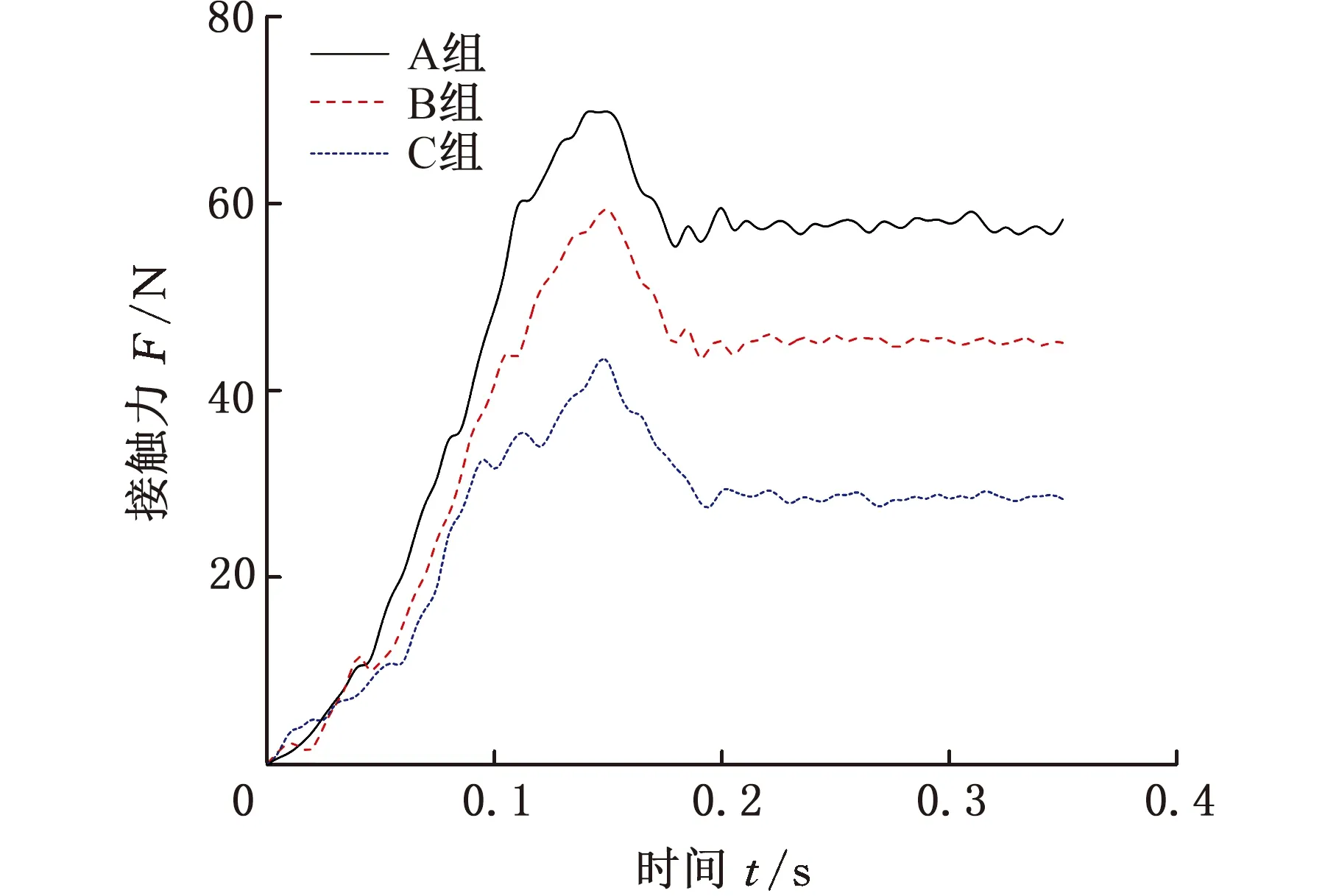
图15 工件接触力曲线图Fig.15 Curve of workpiece contact force
说明理论模型基本可用。接触力在砂轮接触到工件后发生明显的变化,最后接触力分别达到动态平衡状态。其中凹面下的接触力大于平面接触力,凸面条件下的接触力最小,验证了2.2节的仿真结果,证实了工件表面曲率与砂轮的拟合程度越高,磨粒群形成接触力越大的规律。
3.3 非一致曲率加工表面的加工试验与结果分析
为了验证提出的非一致曲率表面下的软固结磨粒气压砂轮材料去除模型的正确性,在机器人抛光平台上对三组工件进行抛光。工件的材料为模具钢P20,硬度为HV434。抛光时间为180 s,每隔30 s使用分析天平测量工件质量并记录。
表6所示为本文气压砂轮材料去除模型预测量与未考虑工件曲率变化的原始模型预测量对比情况。图16所示为三组工件表面下材料去除量与预测模型的对比情况。

表6 气压砂轮材料去除量预测表

(a)A组表面材料去除量对比
图16显示了不同曲率对软固结磨粒气压砂轮材料去除量的影响,可以看出,工件的曲率与砂轮曲率的拟合度越高,材料去除量越大。在抛光试验的前期,材料去除量较大,随着试验的进行,材料去除量逐渐减小。比较修正的预测模型与试验结果之间的平均绝对值误差(MAE)可得:凹面0.068,平面0.118,凸面0.098,修正模型的MAE均值为0.095,未修正模型预测值与试验结果的MAE均值为0.291。修正后的预测模型与试验结果的趋势一致,且在数值上有更好的拟合效果。
采用软固结磨粒气压砂轮加工上述三组工件。使用光学3D表面轮廓仪SuperView W1对工件表面形貌进行观测,所得工件的表面形貌见图17。
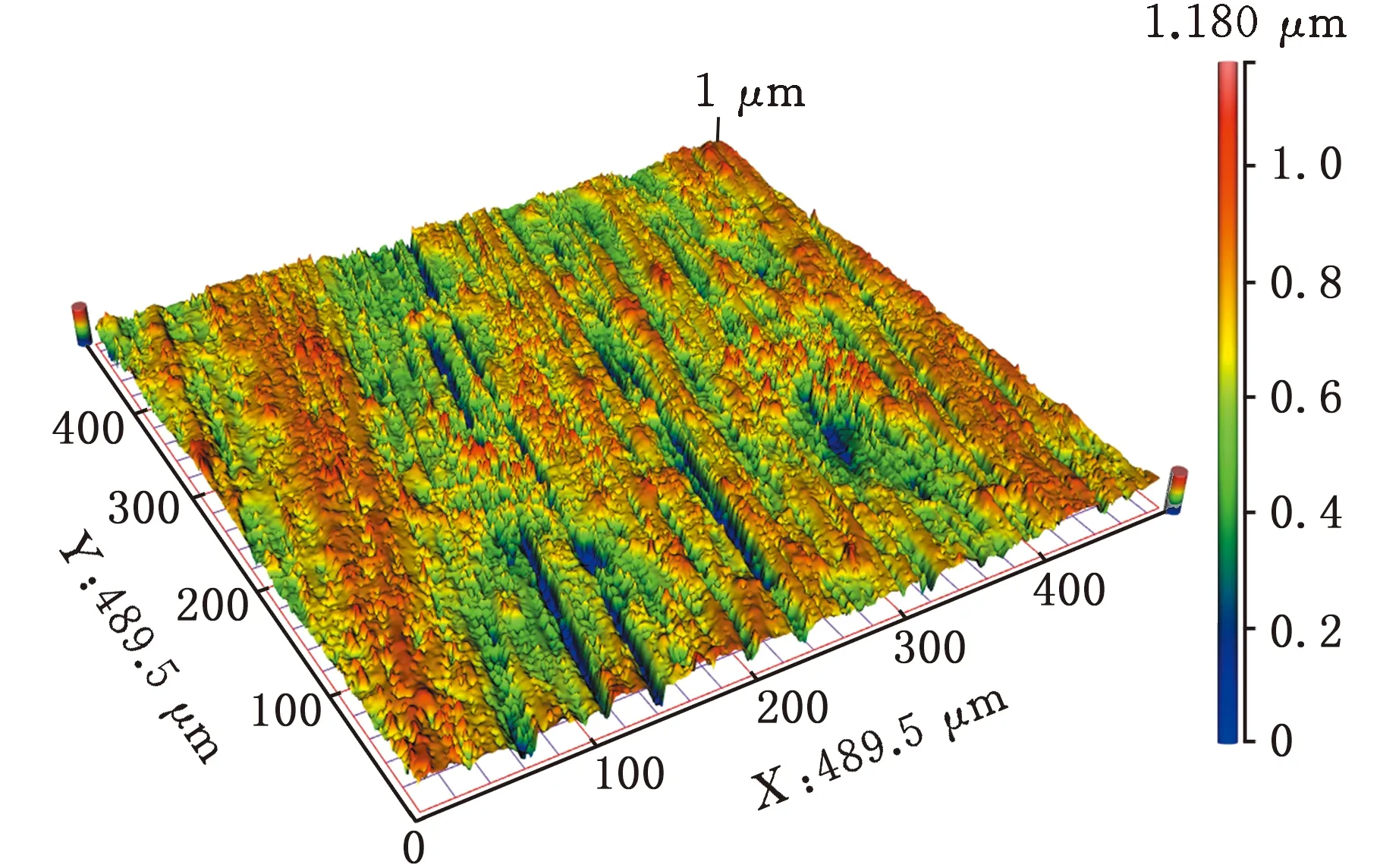
(a)原始形貌
由图17可以看出,加工后工件表面质量良好,具有较高的一致性,砂轮曲率与凹面的拟合程度高,磨粒速度突变程度小,其表面划痕最少,平面次之。
4 结论
(1)从细观角度分析了软固结磨粒气压砂轮中磨粒群的剪胀效应,引入非共轴系数,修正了Rowe剪胀模型。结合层状弹性理论,建立了非一致曲率接触面下的气压砂轮接触力学模型。
(2)根据软固结磨粒气压砂轮接触特性,分析抛光接触区磨粒速度变化规律。针对非一致曲率的接触条件,建立了接触区磨粒的速度模型。结合修正的Preston方程建立了软固结磨粒气压砂轮的材料去除模型。
(3)采用颗粒流仿真软件EDEM进行仿真,研究了软固结磨粒气压砂轮在不同曲率表面下的接触力大小、接触区速度场变化。工件表面曲率与砂轮曲率拟合程度越高,抛光力越大,且接触区内磨粒速度突变程度小,运动方向的一致性高。
(4)进行了软固结磨粒气压砂轮的加工试验。将工件分成三组,通过材料去除试验,验证了非一致曲率下的软固结磨粒气压砂轮的材料去除率模型的正确性,该模型可以用于气压砂轮抛光试验中材料去除的定量分析。在砂轮的下压量为1.5 mm时,工件的划痕得到明显改善,与砂轮曲率拟合程度高的凹面工件表面质量最高。
