一种脊线提取方法在轴承故障诊断中的应用
2021-05-27黄凯旋蔡坤奇刘圆圆刘幸福
陈 剑 杨 斌 黄凯旋 蔡坤奇 刘圆圆 刘幸福
1.合肥工业大学噪声振动研究所,合肥,2300092.安徽省汽车NVH工程技术研究中心,合肥,230009
0 引言
滚动轴承是旋转机械的重要组成部件,被广泛应用于航天、冶金、交通运输等行业。因工作环境恶劣、载荷变换不定等因素,滚动轴承成为最容易出现故障的部件之一。运转中的轴承一旦出现故障可能会导致机械损坏,甚至会造成重大的安全事故,因此,对滚动轴承的工作状态进行监测具有重要的工程意义。
时频分析方法近年来被广泛应用于各学科领域的信号分析处理,如地质学[1]、语音[2]、通信[3]、机械工程[4]等。滚动轴承故障振动信号大多是非平稳信号,时频分析方法在分析该类信号时相比于时域和频域分析方法更有优势。郑近德等[5]提出了一种自适应无参经验小波变换方法,并将其与希尔伯特变换结合,成功诊断出转子运转过程中的局部磨损故障;张尚斌等[6]在研究列车轴承故障诊断中,为解决列车运动所产生的多普勒频移和扩展问题,提出了一种时频幅值匹配的多普勒校正方法;丁夏完等[7]针对传统短时傅里叶变换(STFT)带宽固定问题,提出了一种以三阶B样条函数作为窗函数的自适应STFT,并应用于滚动轴承的故障诊断,取得了良好的效果。时频分析方法提供了时域和频域的联合分布信息,可以获取信号的瞬时频率特征。关于瞬时频率的提取方法,徐晓迪等[8]将时频谱在时频平面上进行压缩重排,从而提取频谱上的能量脊线,克服了脊线提取不完整的缺点;王超等[9]通过小波系数的局部模极大值初步提取小波脊,并施加罚函数来平滑小波脊的不连续性,最后采用动态规划的方法得到了新的小波脊;汪晓珊等[10]提出了一种频谱集中性指标,通过粒子群优化算法找到该指标的最优值,进而估计对应的初始频率参数。
虽然很多学者对瞬时频率的估计方法做了大量研究,取得了不少研究成果,但是瞬时频率的提取依然存在很多困难,例如信号中干扰噪声能量较大时瞬时频率提取的准确率难以保证,提取过程中需要对信号进行各种繁琐的处理,不能同时提取多个不同的特征频率等。针对以上问题,本文提出一种改进的Crazy Climber算法,在一定程度的强噪声干扰情况下,实现了多个瞬时频率的同时提取,提高了瞬时频率提取的准确性。
1 基本原理
1.1 短时傅里叶变换
STFT的基本思想是使用窗函数截断分析信号,使其被分为多个片段信号,将这一系列片段信号视为平稳信号并分别进行傅里叶变换,从而得到不同频率分量在时域上的变化情况。定义为
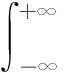
(1)
式中,x(τ)为分析信号;g(τ-t)为窗函数;g*表示共轭;F(t,f)为分析信号在时刻t的频谱。
对于离散数字信号,其离散的STFT为
(2)
式中,g(k)为窗函数的离散形式;m为离散后的时间段;F(m,f)为一个二维的复矩阵,行对应采样时间点,列对应频率值。
对F(m,f)求模得到时频幅值矩阵:
S(m,f)=|F(m,f)|
(3)
STFT常使用的窗函数有Hamming窗、Hanning窗、Gaussian窗和Blackman窗,本文在对信号进行STFT时采用的是Blackman窗。
1.2 脊线提取算法
1.2.1 Crazy Climber算法
时频分析过程中,时频脊线的提取对确定某一时刻的频率信息尤为重要,目前的脊线提取方法对多源脊线的提取较为困难,且信号中的噪声干扰较大时,时频脊线提取效果不佳。针对此问题,CARMONA等[11]提出一种Crazy Climber算法,实现了多源脊线同时提取。该算法将一系列按一定规则运动的点(Climber)视为密度分布,所有点按照相同的规则在平面上运动,并逐渐被脊线位置所吸引,从而聚集在脊线位置上,使得Climber对脊线位置的访问次数远远高于其他位置,通过对各位置访问次数进行统计获得度量矩阵,再对度量矩阵进行局部最优峰值提取,并将度量值较高的位置连接起来即可获得脊线。采用Crazy Climber算法提取脊线的过程包含度量矩阵获取和局部最优峰值提取两个过程。
若信号的时频矩阵S为M×N矩阵,则使用Crazy Climber算法对其进行脊线提取的具体步骤如下。
(1)初始化K个Climber、度量矩阵D、观测矩阵R以及Climber移动次数n。K个Climber均布在与时频矩阵S维度相同的观测矩阵R中,D初始化为与S维度相同的零矩阵。
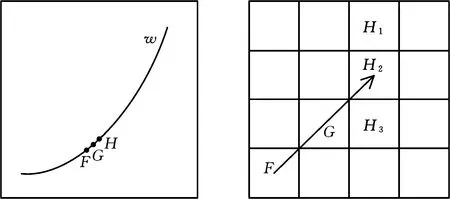
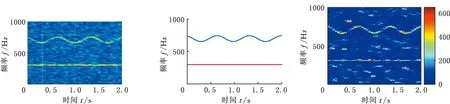
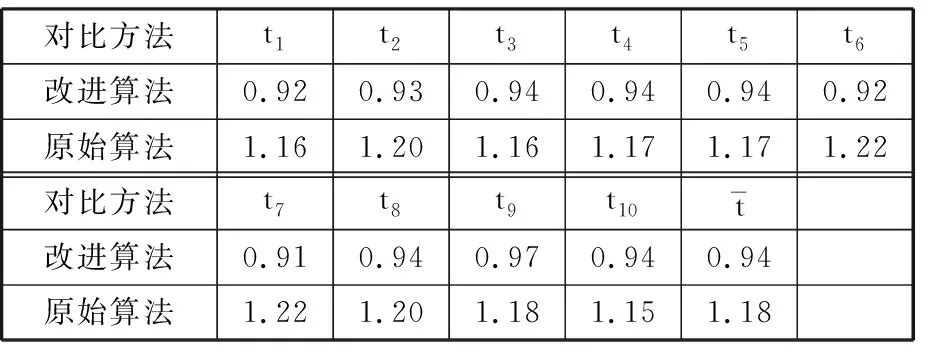
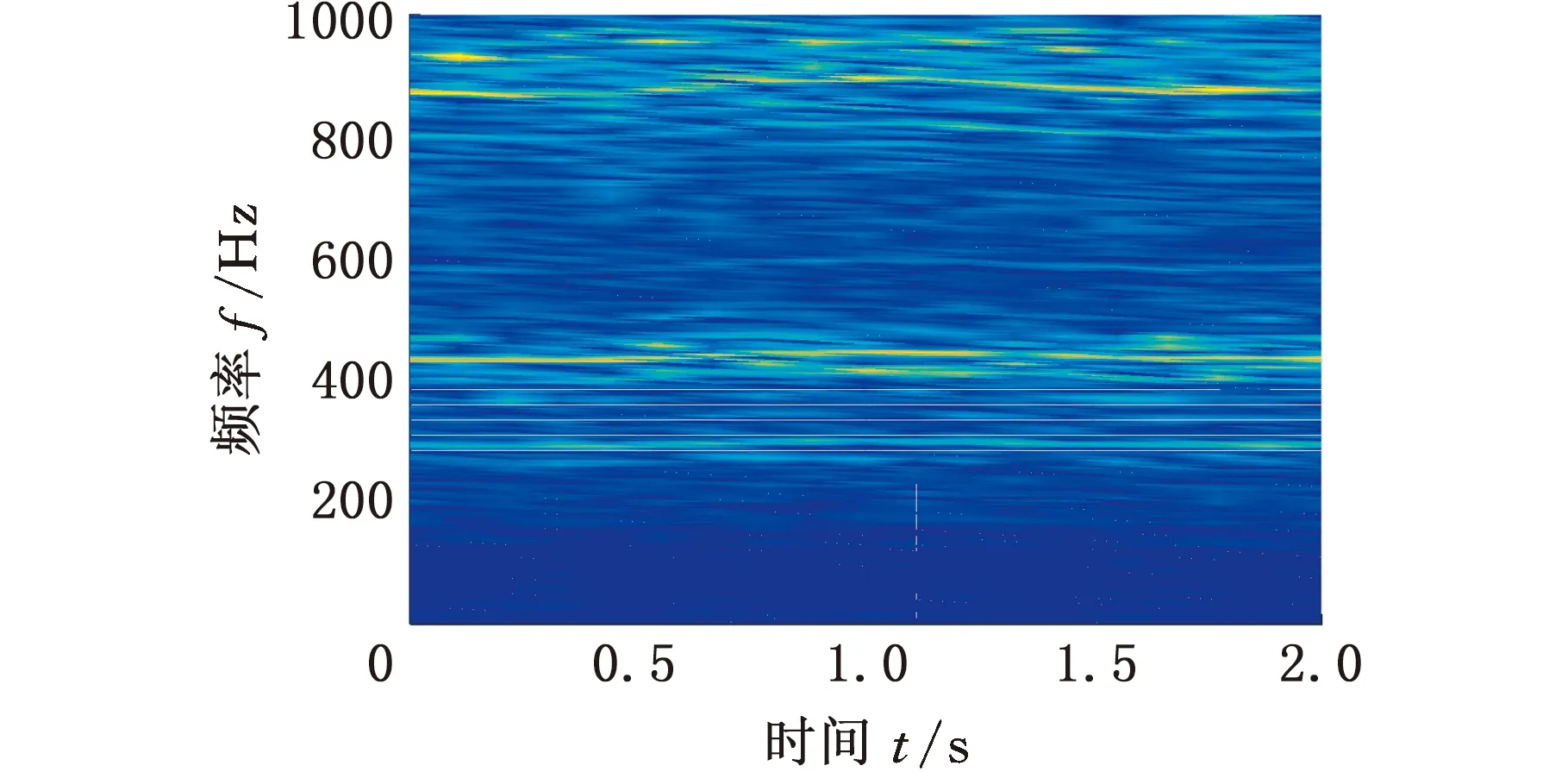
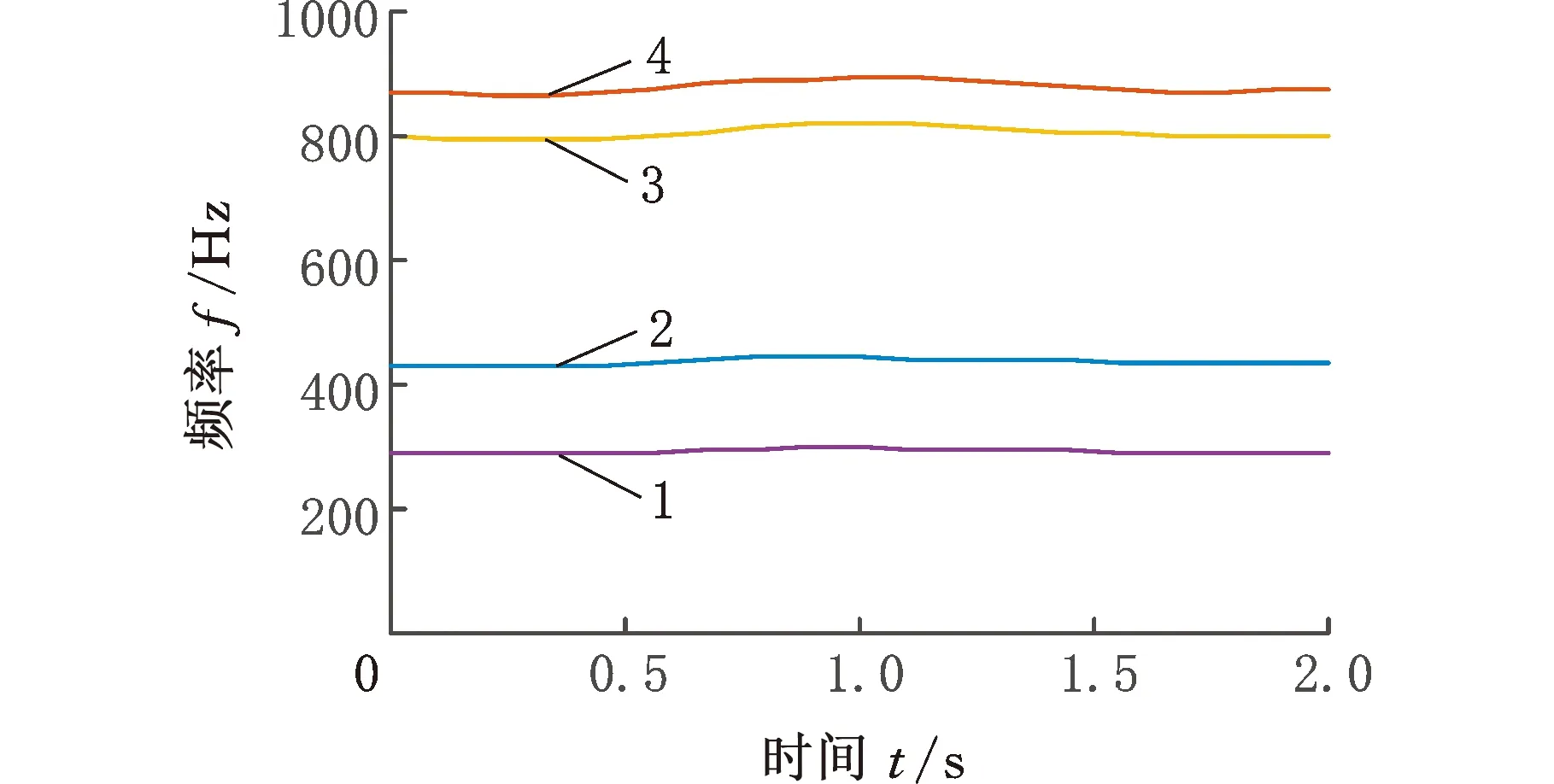
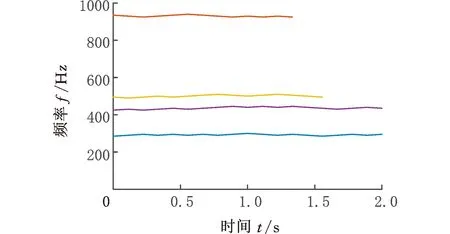
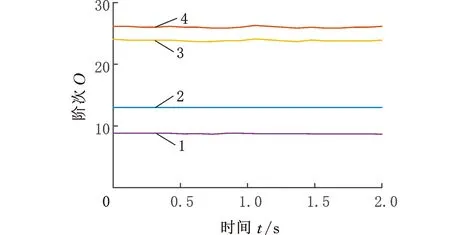
(2)Climber每次移动对应的时间用tk(k=1,2,…,n)表示,若tk时刻Climber的位置R(tk)=(i,j),则tk+1时刻Climber的位置R(tk+1)=(i′,j′)由以下规则确定:①Climber进行水平方向上的移动,若Climber在R内部(2≤j≤N-1),则tk时刻,Climber以1/2的概率左移或右移一列,即j′=j-1或j′=j+1;若Climber在R边界处(j=1或j=N),j=1时,j′=2,即Climber在左侧边界时,直接向右移动一列,j=N时,j′=N-1,即Climber在右侧边界时,直接向左移动一列。②水平方向的移动完成后,进行竖直方向的移动,该方向的移动规则与水平方向不同,首先以相同的概率上移一行(i″=i-1)或下移一行(i″=i+1):若S(i″,j′)>S(i,j′),则i′=i″;若S(i″,j′) pk=exp((S(i″,j′)-S(i,j′))/Tk) (4) Tk=(max(S)-min(S))/(lbk) (5) (3)移动完成后,在度量矩阵D的相应位置上增加度量值1,即Dk+1(i′,j′)=Dk(i′,j′)+1。 (4)重复步骤(2)、步骤(3),直到移动次数达到设定值,迭代结束,获得整个度量矩阵Dn。 (5)对度量矩阵Dn在时间方向进行递归,给定任一点(i,j),在(i,j+1)和(i±1,j+1)里寻找最优的相邻点,并与之形成一条脊线。 (6)重复步骤(5),直到所有满足要求的点都在脊线中,形成整个时频面的脊线。 (7)计算每条脊线的长度,设定长度阈值,剔除长度小于阈值的脊线,剩下的脊线即为提取的时频脊线。 需要说明的是,在进行第(5)步之前,考虑到噪声影响,需要设定一个阈值e用于将脊线从Dn的低度量值中区分出来: (6) e一般为整个度量矩阵度量均值的倍数或最大度量值的小数倍。 上述脊线提取过程中,步骤(1)~步骤(4)为度量矩阵获取过程,步骤(5)~步骤(7)为提取局部最优峰值获取时频脊线过程。 1.2.2改进的Crazy Climber算法 Crazy Climber算法虽然能够实现多条脊线同时提取,但是依然存在许多不足之处。首先,在度量矩阵获取过程中,效率不高,即需要经过很多次迭代才能使脊线位置的度量值与其他位置的度量值有明显的区分,主要原因是Climber水平方向的移动具有随机性,竖直方向上的移动虽然有规定的准则,但是随机性也比较强,同时,当Climber位于矩阵边界时,只能反方向移动,这使得该Climber又重复移向已经移动过的位置,导致其遍历全部位置的速度较慢,无法快速准确地向脊线位置移动。其次,在局部峰值提取获得脊线的过程中,获取的脊线不够平滑、准确,导致无法正确提取瞬时频率。为了解决以上两个问题,本文提出了改进的Crazy Climber算法。 (1)针对度量矩阵获取效率低的问题,提出改变Climber在时频空间的移动规则,使其能够更加快速地向脊线位置移动。若tk时刻Climber对应的位置R(tk)=(i,j),则tk+1时刻Climber对应的位置R(tk+1)=(i′,j′)确定规则如下。 Climber以一定的概率向相邻的6个位置移动,这6个位置用Au(u=1,2,…,6)表示,见图1,移动到Au的概率pu由时频矩阵中Au位置对应的频率幅值相对于R(tk)位置的频率幅值的增量ΔAu决定: (a)非边界Climber可移动位置 (7) 增量越大,移向该位置的概率也越大。为避免ΔAu出现负值,进行如下处理: ΔA′u=ΔAu+|min(S(Au))-S(R(tk))| (8) Climber移动到Au的概率 (9) ①当R(tk)位于矩阵内部时(2≤i≤M-1且2≤j≤N-1),则tk+1时刻Climber可能移向的6个位置如图1a所示。此时Au对应于时频矩阵中的坐标为A1(i-1,j-1)、A2(i,j-1)、A3(i+1,j-1)、A4(i-1,j+1)、A5(i,j+1)、A6(i+1,j+1)。 ②当R(tk)位于矩阵边界时,则tk+1时刻Climber可能移向的6个位置如图1b所示。对时频分布矩阵进行首尾对应相接,得到相应的Au点视为tk+1时刻Climber可能移向的位置。此时,图中Au对应于时频矩阵中的坐标为A1(i-1,j-1)、A2(i,j-1)、A3(1,j-1)、A4(i-1,j+1)、A5(i,j+1)、A6(1,j+1)。 需要说明的是,图1b中只是R(tk)在矩阵边界上的一种情况,其他情况下,Au的位置变换与此种情况类似。 Climber按照以上的规则进行移动,能够确保其移动趋势方向始终朝着脊线方向,同时当Climber移向矩阵边界处后无需返回,使其能够更加快速地对全部位置进行度量,极大地提高了度量矩阵的获取效率和质量。 (2)针对局部峰值提取脊线的过程中,提取的脊线不够平滑、准确这一问题,对原有的局部峰值提取方法进行改进,通过多点共同决定局部峰值点的位置来提高脊线的准确性和平顺性。 旋转机械工作过程中,转动部件对应的频率与机械转速有关,由于转速变化是连续变化过程,这就使得时频图中转动部件对应的频率是光滑连续的曲线。 如图2a所示,设w为时频图中一条脊线,F、G、H为w上三个相邻的点,F为t-1时刻点,G为t时刻点,H为t+1时刻点,在对H点位置进行确定时,其位置应在点G的斜率方向附近,如图2b所示,F、G两点之间的连线方向为点G的斜率方向,指向t+1时刻的H2点,H1和H3为H2在竖直方向附近的点,那么H点的位置可认为是H1、H2、H3中最大值对应的位置。将此方法用于度量矩阵的局部最优峰值提取,具体提取方法如下:对于时频图中的某一条脊线,t-1时刻和t时刻该脊线对应于度量矩阵中的位置分别为Et-1(it-1,jt-1)、Et(it,jt),则t+1时刻的位置应为(2it-it-1,jt+1)和(2it-it-1±1,jt+1)中最大度量值对应的位置。另外,当t时刻是开始时刻时,由于此时t-1时刻不存在,则t+1时刻的位置为(it,jt+1)和(it±1,jt+1)中最大度量值位置。 (a)脊线图 (b)局部峰值提取图图2 局部最优峰值提取示意图Fig.2 Diagram of local optimal peak extraction 可以看出,该方法在进行局部最优点选取时,局部最优点由前两个局部最优点的位置共同决定,提高了提取脊线的平顺性和准确性。 阶次分析是分析旋转机械运动部件故障的一项重要技术。阶次是旋转部件因旋转造成的振动响应,它独立于部件的实际转速,是参考轴转频的倍数或分数。如滚动轴承由内圈、外圈、滚动体、保持架四个部分组成,这四个部分发生故障时对应的阶次分别为Oi、Oo、Oe、Oc,则 (10) (11) (12) (13) 式中,Z为滚动体的个数;d为滚动体的直径mm;D为轴承的节径,mm;α为接触角。 为验证改进的Crazy Climber算法在时频分析中的有效性,构造含有白噪声的仿真信号x(t): (14) 其瞬时频率为 (15) 该仿真信号的采样频率fs=10 240 Hz,式中,t=[0∶1/fs∶2],η(t)为信噪比为1dB的高斯白噪声。x(t)时域波形如图3所示。 对仿真信号进行短时傅里叶变换,得到时频矩阵,分别使用改进的Crazy Climber算法和原始Crazy Climber算法对时频矩阵进行脊线提取,两种算法中Climber移动次数设为100,度量矩阵度量值的阈值为最大度量值的0.1倍,脊线长度阈值为时频矩阵宽度的0.5倍。仿真信号脊线提取如图4所示。 (a)时频图 (b)实际频率脊线图(c) 改进Crazy Climber算法获得的度量矩阵图 从图4c中可以看出,度量矩阵图中脊线位置处的度量值远远高于其他位置,而图4d中频率f2的脊线位置度量值较高,但是频率f1的脊线位置度量值与非脊线位置的度量值区分度不大,导致其不能被明显地区分。对图4c、图4d的度量值进行分析,可以看出图4c中脊线处的最大度量值超过了600,而图4d中脊线处的最大度量值小于200,因此在相同的移动次数下,改进的Crazy Climber算法获得度量矩阵的质量更高,提高了识别脊线的能力。当原始算法的移动次数设定为230时,可以获得最大度量值与图4c相当的度量矩阵,即当改进算法与原始算法的移动次数分别设定为100和230时,两者获得的度量矩阵质量大致相同,在此条件下,对两种算法所需要的时间进行统计。为确保结果的可靠性,每种算法分别进行10次试验,各次试验的结果取平均作为最终结果,结果如表1所示,可以看出改进算法需要的时间为0.94 s,原始算法需要的时间为1.18 s,因此获得相同质量的度量矩阵,原始算法消耗的时间更长。 表1 两种方法消耗时间对比表 (16) 式中,a为提取脊线的长度;Yr为提取脊线的第r个频率值;yr为实际脊线的第r个频率值。 综上分析,相比于原始Crazy Climber算法,改进的Crazy Climber算法不仅具有更强的脊线识别能力,而且提取脊线的准确性和完整性也可以得到保证。 为验证改进的Crazy Climber算法在轴承故障诊断中的有效性,对一外圈故障的圆柱滚子轴承进行试验,轴承上的故障特征通过线切割制造,试验台总体结构见图5,试验轴承为NSK 公司的NU1010型圆柱滚子轴承,通过加速度传感器和信号采集系统实现轴承振动信号的采集。试验过程中,轴承转速为2000 r/min,采样频率fs=20 480 Hz。表2所示为试验轴承的相关参数,表3所示为该轴承各零件的故障特征阶次。 图5 试验台总体结构Fig.5 Structure of the test bench 表2 轴承相关参数 表3 轴承故障阶次 从采集的数据中抽取40 960个样本点,然后使用STFT进行时频变换,获得时频矩阵,图6所示为时频图谱(为方便分析,只对1000 Hz以内的频率进行显示);然后使用改进的Crazy Climber算法对时频矩阵进行脊线提取,提取过程中Climber移动次数设为300,度量矩阵度量值的阈值为最大度量值的0.1倍,脊线长度阈值为时频矩阵宽度的0.5倍,结果如图7所示,可以看出,时频图中明显的脊线被完整地提取出来。可以发现,在0.5~1.5 s这段时间,各条脊线对应的频率发生了变化,使得脊线向上凸起,这是试验过程中电机转速不稳定导致的瞬时频率波动现象。 图6 故障信号时频图Fig.6 Time-frequency spectrum of fault signal 图7 改进Crazy Climber算法脊线提取结果Fig.7 Ridge extraction result of improved CrazyClimber algorithm 为验证该改进算法的效果,将其与原始Crazy Climber算法进行对比,使用原始算法对故障信号进行脊线提取过程中,各参数与改进算法脊线提取过程的参数设置相同,其提取结果如图8所示,可以看出,部分脊线提取不完整,且脊线不够平顺,与时频图中的真实脊线差距较大。 因此,改进的Crazy Climber算法总体上优于原始Crazy Climber算法。 图8 原始Crazy Climber算法脊线提取结果Fig.8 Ridge extraction result of original CrazyClimber algorithm 为实现轴承的故障诊断,对各脊线对应的阶次进行提取,由于时频图中没有出现明显的基频脊线,所以提取的脊线中也不包含对应基频的脊线。在该试验工况下,轴承的基频为fr=33.3 Hz,分析提取的脊线发现,第2条脊线的频率对应于基频的13倍频,即f2=13fr,因此,可以用第2条脊线各时刻频率的1/13来代替整个过程中基频各时刻的频率,所以fr=f2/13,将各脊线与fr作商即得到对应的阶次,结果如图9所示。计算各脊线阶次的平均值,结果如表4所示,可以看出,第2、3、4条脊线对应的都是基频的整倍频,第1条脊线的阶次与轴承外圈故障阶次接近,可以判断该轴承外圈出现故障,诊断结果与实际相符,证明本文提出的改进Crazy Climber算法在实际应用中可以有效识别轴承故障。 图9 故障信号特征频率对应阶次Fig.9 Corresponding orders of fault signal 表4 各脊线对应阶次 (1)针对Crazy Climber算法度量矩阵提取效率低的问题,提出一种有效的Climber移动规则,实现了度量矩阵快速准确的获取,提高了脊线提取的完整性。 (2)对Crazy Climber算法中局部最优峰值的提取方法进行改进,提高了提取脊线的准确性。 (3)将改进的Crazy Climber算法应用于轴承的故障诊断中,通过阶次分析可准确地判断轴承的故障类型。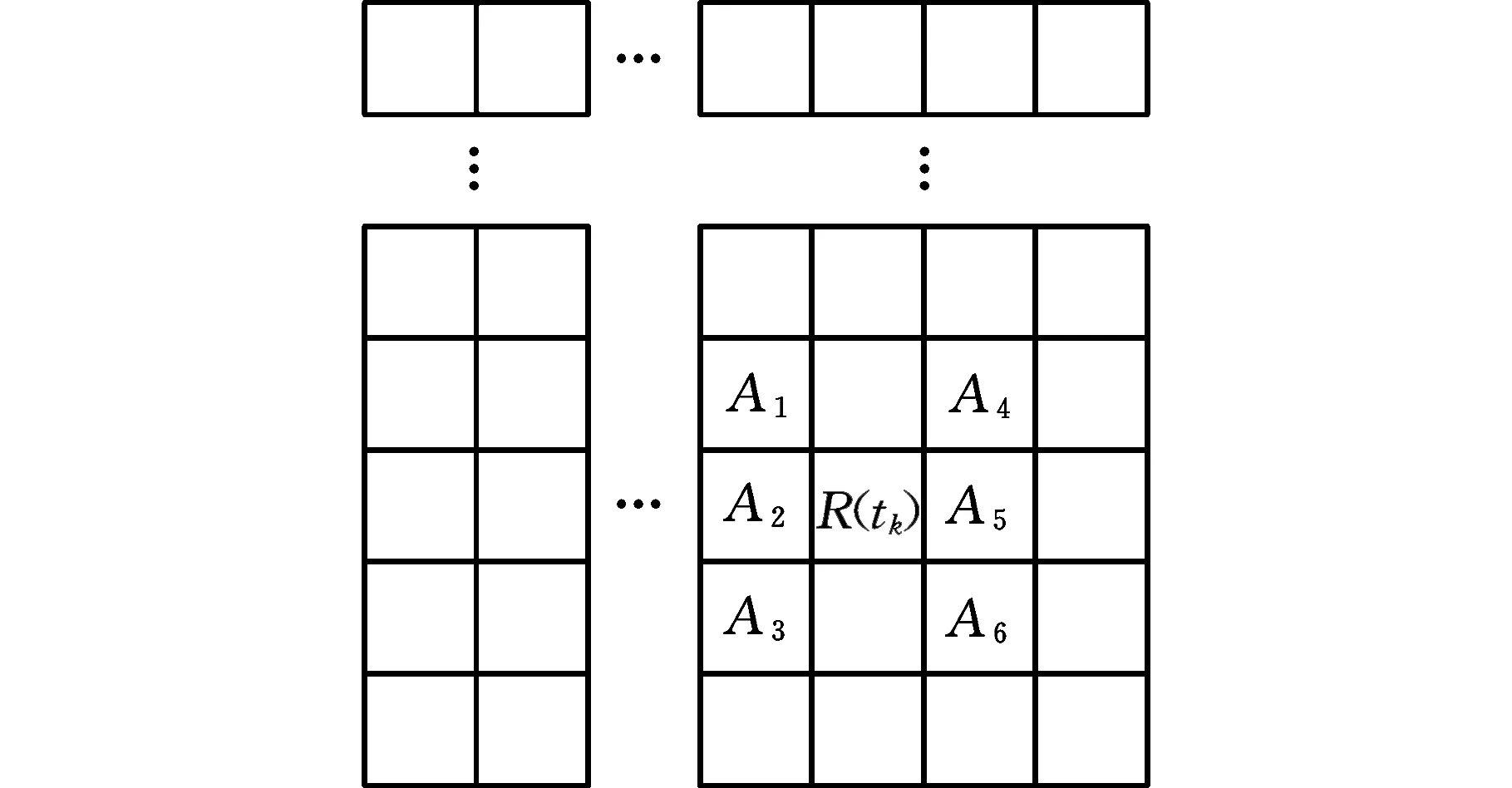
1.3 阶次分析
2 仿真信号分析
2.1 仿真信号构造
2.2 脊线提取
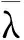
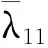
3 试验分析




4 结论
