基于改进逼近理想解的排序技术方法自发电缓冲背架性能优化

向 宇,王亚平,王永敢,步春辰

(南京理工大学 机械工程学院,江苏 南京 210094)

近年来可穿戴设备迅速发展,广泛应用于日常生活、科研或军事活动中[1]。但是电池存储能量的限制,严重制约了穿戴设备的使用和推广。为了解决穿戴式设备的能源问题,人们提出了从环境中获取能量的解决途径。

自20世纪90年代以来,从人体运动中获取能量的想法逐渐成为研究热点,特别是收集人体背负背包行走过程中产生的能量。Rome等[2]开发了悬挂式的负重背包,将人体运动的机械能转化成电能,为移动设备充电。袁志高等[3]利用弹簧质量振动系统带动齿轮齿条运动,驱动与齿轮连接的发电机产生电能。王俊龙[4]设计了一个通过调整腰间固定机构改变绳长,适应不同人群的无框架单向轴发电背包,在1.11 m/s人体行走速度下背负1.5 kg大约能获得0.3 W的能量。陈秋兴等[5]利用配有单向轴的齿轮将齿条的上下运动变成了单向运动,提高了收集能量的效率。但是上述研究仍存在参数不可调的缺点,无法适应在不同步态条件下的运动,背包发电功率不高;另外其偏重于提高发电效率,忽略了行走过程中背包对人体的冲击影响,特别是在背负载荷较重的情况下,普遍存在提高发电效率的同时人体所受冲击明显增加的问题。曹自平等[6]设计了一个通过调节线圈与永磁体的间距,自适应调节载荷板振动阻尼的发电背包,靠弹簧和线圈产生的阻尼力在一定程度下实现悬浮减重。Tang等[7]研究了具有调谐质量阻尼器的能量收集和振动控制的结构,但是无法调节系统刚度,且附加质量较大。Xie[1]采用调节弹簧拉伸比来实现系统的变刚度,考虑了发电效率和冲击之间的关系,但需要在不同步态条件下进行手动调节,使用不便,调节不及时还会造成不必要的能量损失。

本文提出了一种自发电缓冲背架优化控制策略,根据人体行走步频和步幅的变化,通过自动调整系统的刚度和阻尼大小,来实现减少人体所受冲击载荷、提高背包发电功率的目的。首先采用改进的非支配排序遗传算法(Non-dominated sorting genetic algorithm-Ⅱ,NSGA-Ⅱ)进行全局寻优,求得最优Pareto解集,使用熵权法和改进的基于加权广义(Weighted Moore-Penrose,WMP)的马氏距离的逼近理想解的排序技术(Technique for order preference by similarity to ideal solution,TOPSIS)对Pareto解集排序,获得在不同行走步态和不同载荷下背架的刚度和阻尼参数的最优值,为自发电缓冲背架的研制提供依据。

1 自发电缓冲背架分析模型

自发电缓冲背架结构如图1所示,由背架、缓冲装置、发电装置3大部分组成,在背架与背架负载之间安装缓冲装置和发电机构;缓冲装置主要由系绳、磁流变阻尼器、导向轮、夹紧调节装置等组成,系绳具有重量轻、阻尼小、抗拉强度好、柔软性好、大尺度及易卷取等优点[8]。发电装置主要采用齿轮发电机,由背负载荷带动齿条齿轮旋转,驱动发电机发电。其控制原理为:人在行走时,背架随着人体上下运动,通过拉力传感器测得绳子拉力以及背负质量,通过加速度传感器测得人体运动步频和幅度,将运动步态信号输入到控制器,经过控制策略控制系统刚度阻尼状态,调整工作绳长实现变刚度,调节可调阻尼的磁流变阻尼器实现变阻尼,从而实现发电功率和人体受力性能的最优。

图1 缓冲背架结构图

1.1 缓冲背架动力学模型

图2为自发电缓冲背架在人体行走时的受力简图。背架与人体在肩部和腰部有肩带和腰带的约束,可以简化为一弹簧阻尼系统,但是由于此处缓冲效果并不明显,因此这里暂不考虑肩带和腰带的缓冲作用,假设背架与人体躯干固连。

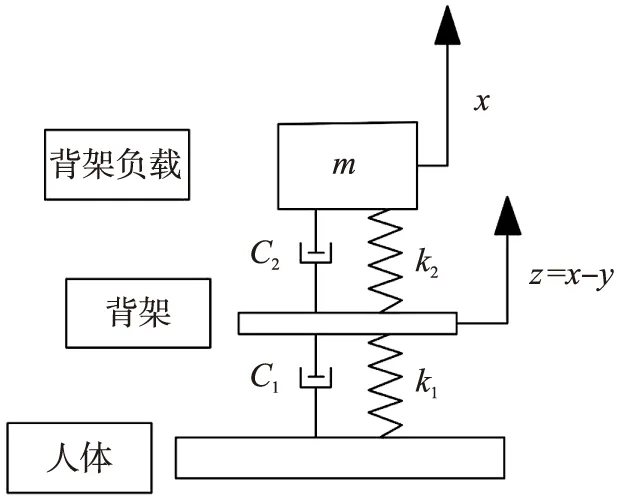
图2 背架受力简图

在背架与背架负载之间是缓冲装置和发电装置的作用。系绳模型一般可以从弹性和质量两方面进行简化[8],本文采用集中质量弹性体模型,将系绳离散成一系列与弹簧、阻尼相连接的质点,当改变绳长时,就改变了串联的弹簧和阻尼器的数量,所以通过绳长的调节实现了改变刚度的目的。虽然绳索张力的变化会使刚度发生变化,但是刚度变化很小,可以忽略不计[9]。除了系绳的缓冲作用外,发电装置也起到一定的缓冲作用,发电机中阻尼系数受摩擦产生的机械阻尼和发电时产生的电阻尼等影响[10],且发电装置阻尼系数为常数。通过控制电流大小,改变磁流变阻尼器的电磁强度,从而改变了系统的阻尼,因此本文将缓冲装置和发电装置共同的作用简化为弹簧-阻尼系统。

背架在垂直方向上的运动y,和人体躯干在垂直方向上的运动一致。人体正常的行走过程分支撑相和摆动相,根据人体行走过程中的规律,人体重心上下运动轨迹可近似为因人体不规则步态而产生的在有限范围内波动的非周期性误差曲线的叠加[11]。因此人体质心的运动y可以表示为

y(t)=Ysin(ωt)

(1)

式中:Y为步幅;w为步行频率;t为时间。

由于缓冲系统的作用,背架负载在垂直方向上产生位移x。人体受力不仅与背架负载对背架的作用力相关,还与背架肩带/腰带的缓冲和缚紧程度有关,这里暂不考虑肩带/腰带的作用,因此人体受力可表达为

(2)

式中:m为背架负载质量;c为缓冲系统阻尼系数;k为缓冲系统刚度系数。

人体受力的幅值为

FT=mω2X+mg

(3)

由于背负负载的作用为常数项,为了简化计算,将此项略去,这里只考虑变化项——人体所受冲击载荷幅值

F=mω2X

(4)

1.2 发电功率模型

根据振动理论[12],背架负载相对于背架的运动距离z与背架位移y具有相同频率的正弦运动,其运动微分方程为

(5)

z的幅值为

(6)

电机运动为单向旋转,人体相对运动向上时发电,向下时脱离啮合。啮合时齿条运动的距离与齿轮转动的长度相等[3],表达式为

(7)

式中:f为振动频率;H为齿条运动长度;n为齿轮转速;r为齿轮半径。

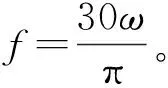
(8)

式中:g=9.8 m/s2;N为发电功率;M为扭矩。

1.3 自发电缓冲背架的多目标优化模型

自发电缓冲背架的优化目标是背包发电功率N、人体所受冲击载荷F。优化变量为缓冲系统中刚度k和阻尼比ζ。

在无缓冲的情况下,背负负载对人体产生的峰值力为F0=mYω2。

自发电缓冲背架要实现减轻人体受力的目的,则需满足以下约束条件:F≤F0。

甄小美脸上露出无奈的神情。我接着说：“那咱们想想，你还能做什么，让自己觉得不无聊，觉得有意思？然后把它做到选择轮里。你看我这个建议怎么样？你要愿意试试，咱们就做；要不愿意试，也无所谓。咱们再想别的……”甄小美习惯了被提问，没等我说完，立刻蹦出：“画画。”

(9)

式中:X=[x1,x2]T=[k,ζ]T。令运动频率ω=2πb,其中b为步数频率。

2 基于加权广义马氏距离的TOPSIS法

TOPSIS法是解决多目标方案决策问题的有效途径。其基本思想是:最优方案应该与正理想方案的距离最近,并与负理想方案距离最远。传统的TOPSIS法存在以下缺点:当增加或减少新的方案,可能产生新的正负理想解,从而改变欧式距离大小,也容易出现逆序现象[13];当两个评价方案的指标数据相同时,两方案的欧式距离也相同,无法判断方案的相对优劣;无法应用于有着相关性的数据。

针对自发电缓冲背架的多目标优化问题,本文提出了基于加权广义马氏距离的TOPSIS法的多属性决策方法。

2.1 加权广义(WMP)马氏距离

马氏距离表示数据的协方差距离。与传统TOPSIS法中采用的欧式距离相比,马氏距离考虑到各种指标的关联程度,从而减少指标之间的相关性的干扰。在实际应用中,如果总体参数的分布未知,可以通过样本的协方差矩阵代替总体的协方差矩阵[14]。

虽然马氏距离相对于欧式距离有着更广的应用,但指标间的协方差必须可逆,当协方差矩阵不可逆时,马氏距离也不存在。为了避免协方差不存在的情况,通过对协方差的奇异值分解,得到广义逆矩阵,并代替协方差的逆矩阵,所得到的马氏距离叫做广义马氏距离[15]。

(10)

加权广义马氏距离不仅解决了量纲的影响、属性间的相关性、马氏距离存在的问题,更加考虑了属性的差异性对决策的影响[16]。

由于协方差矩阵可能会扩大属性间的影响,所以采用相关系数矩阵可以准确描述属性间的影响[17]。

2.2 基于加权广义马氏距离的TOPSIS法

本文提出基于加权广义马氏距离的TOPSIS法。首先采用NSGA-Ⅱ遗传算法,得到最优前端Pareto解集构成初始决策矩阵,然后采用归一化、正规化、标准化等方法将初始决策矩阵无量纲化,接着计算决策矩阵的正负理想解,将矩阵的协方差矩阵进行奇异值分解,得到广义逆矩阵,利用熵权法得到指标的权重值,最后计算正、负马氏距离,获得每个解的贴近度,最大贴近度的解即为最优解,其分析流程如图3所示。

图3 基于改进遗传算法的多属性决策方法流程图

(1)采用改进NSGA-Ⅱ法获得多个Pareto解所构成的解集建立决策矩阵。根据研究对象选取评价指标(绝对值),若有m备选方案n个指标,即可建立如下决策矩阵X=(xij)m×n,其中i=1,2,…,m;j=1,2,…,n。

(3)采用熵权法[18]计算对应指标的权系数,得到权重矩阵Ω。

(11)

对应指标的权系数为

(12)

(4)求解正负广义加权马氏距离。

决策矩阵{yij}到正理想距离的距离为

(13)

决策矩阵{yij}到负理想距离的距离为

(14)

(5)计算对应方案的贴近度,并对方案排序。

对应方案的贴近度为

(15)

根据Ci大小进行排序,Ci值反映了方案的相对优劣,Ci越大,方案越好,反之,越差。

3 正常步态条件下性能优化结果分析

在正常步态条件下,背负质量m=20 kg,步频b=2 步/s,步行幅度Y=0.05 m。设置NSGA-Ⅱ算法的种群大小为40 000,最优前端系数为0.2,迭代优化的终止条件:进化迭代数为200,终止迭代数为200,适应度函数偏差值为1×10-100。图4为NSGA-Ⅱ算法迭代终止时,8 000个Pareto最优解的分布情况,f1、f2分别为发电功率和人体所受冲击载荷。可知,人体所受冲击载荷与发电功率时成正相关,即发电功率越大,人体所受冲击载荷越大。

图4 正常步态条件下的Pareto最优解集

由于本文算法需要在单片机上实现,考虑到单片机的内存和计算能力,本文对不同样本量(40～8 000)下的权值进行了对比,以8 000样本量权值为基准,进行了误差分析,结果见表1。可以看出样本量变化对误差变化规律不明显,样本量为40时误差小于10%,可以满足设计需求,且该样本量下的最高贴近度方案与8 000样本量一致。因此本文采用Pareto最优解解集样本量为40。

表1 不同样本量下的权值及误差对比

采用信息熵权法计算各属性的权重,通过TOPSIS法对上述40种方案进行相对贴近度排序。本文对比了基于熵权法的TOPSIS法、基于熵权法的线性加权法、基于加权广义马氏距离TOPSIS法3种方法。

基于熵权法的TOPSIS法得权值为w=[0.5612 0.4388],方案8的贴近度最高,[f1,f2]=[0.0394 1.0386],[k,ζ]=[0.01012 0.0084]。

基于熵权法的线性加权法,方案12得分最高,[f1,f2]=[0.0747 143.0286],[k,ζ]=[0.0108 1500.9603]。

基于加权广义马氏距离的TOPSIS法,权值w=[0.4417 0.5583],第25个方案贴近度最高,[f1,f2]=[0.0559 67.2736],[k,ζ]=[0.0115 943.0357]。

3种方法优选结果如表2所示。

表2 3种方法优选结果

可以看出,加权广义马氏距离TOPSIS法,相对于熵权(欧式距离)TOPSIS法的发电功率f1提高了41.88%,相对于熵权线性加权法人体所受冲击载荷f2减小了52.96%,加权广义马氏距离TOPSIS法得到的结果更加符合需求。

4 不同步态参数的影响分析

人体实际行走过程中,步态是不断变化的。本文对不同步态参数情况下,针对加权广义马氏距离TOPSIS方法的适应性展开分析。

选取背负质量m、步频b和步幅Y3个步态参数进行分析。取m=10、20、30、40和50 kg。取b=1.5、2、2.5、3和3.5 步/s。取Y=0.03、0.04、0.05、0.06和0.07 m。图5为不同步态参数组合情况下获得的最优方案值散点图。

通过权数w=[0.6189 0.3811]划分坐标轴。人体受冲击载荷越小,发电功率越大,缓冲背架性能越好,因此第四象限为最优域,第二象限为最差域。由图5可知,分布在第二象限的试验点有7个;而分布在第四象限的点有24个。其中最差点分布比例占5.6%,而最差点大部分处在步频和步幅较大的步态,最优点分布比例占19.5%,背架综合性能在不同步态情况下相对较优占94.4%,所以本文控制策略对不同步态具有良好的适应性。

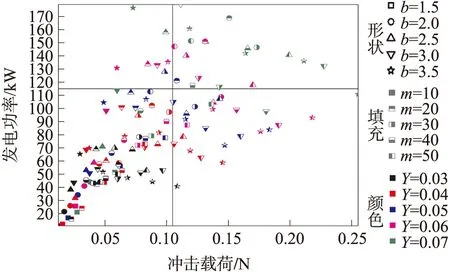
图5 发电功率与冲击载荷的曲线图

(1)背负质量m影响分析。

不同背负质量情况下背架性能曲线如图6所示,将步频和步幅相同的点连接成线。发电功率基本上随着背负质量增大而增大,人体所受冲击载荷随背负质量变化不具明显规律性。

图6 不同背负质量下的曲线图

(2)步频b影响分析。

在不同步频情况下背架性能曲线如图7所示,将背负质量和步幅相同的点连接成线。发电功率基本上随着步频增大而增大,而步频小于2时人体所受冲击载荷随步频增加而增加,步频超过2人体所受冲击载荷变化不具明显规律性。

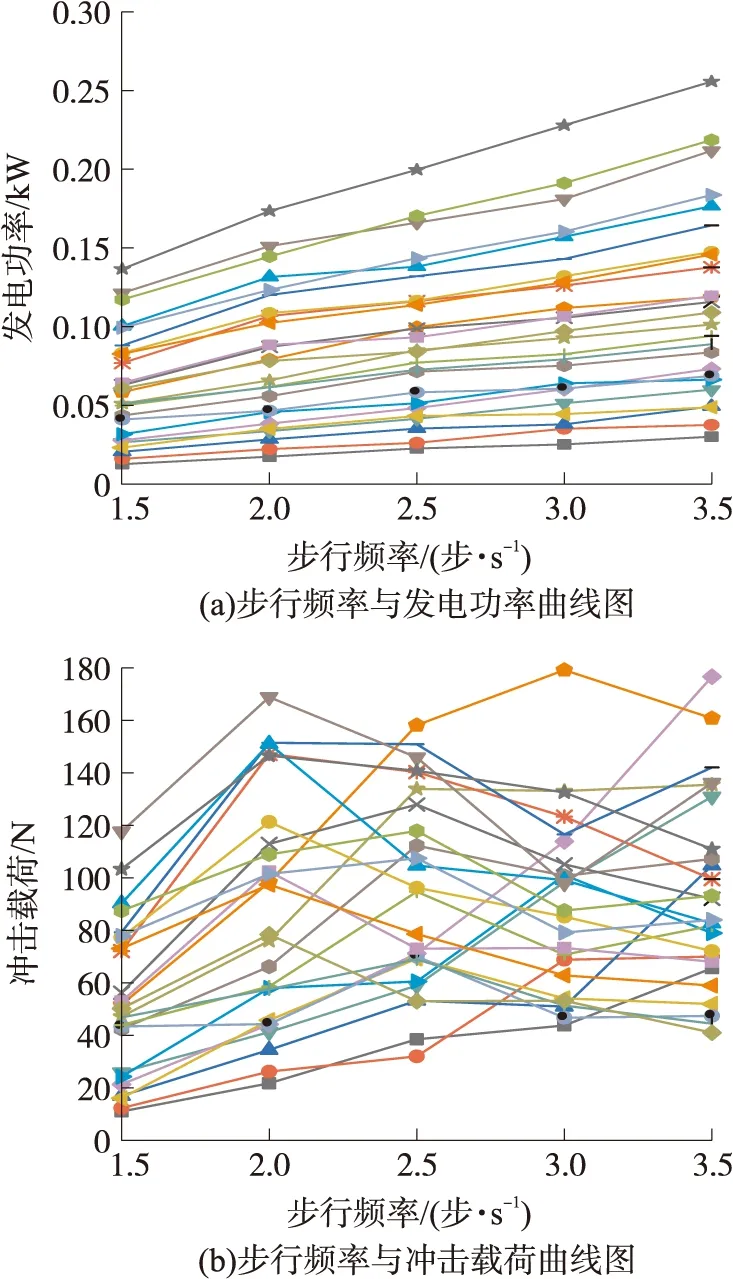
图7 不同步频下的曲线图

(3)步幅Y影响分析

在不同步幅情况下背架性能曲线如图8所示,将背负质量和步幅相同的点连接成线。发电功率基本上随着步幅增加而增加,人体所受冲击载荷变化不具明显规律性。

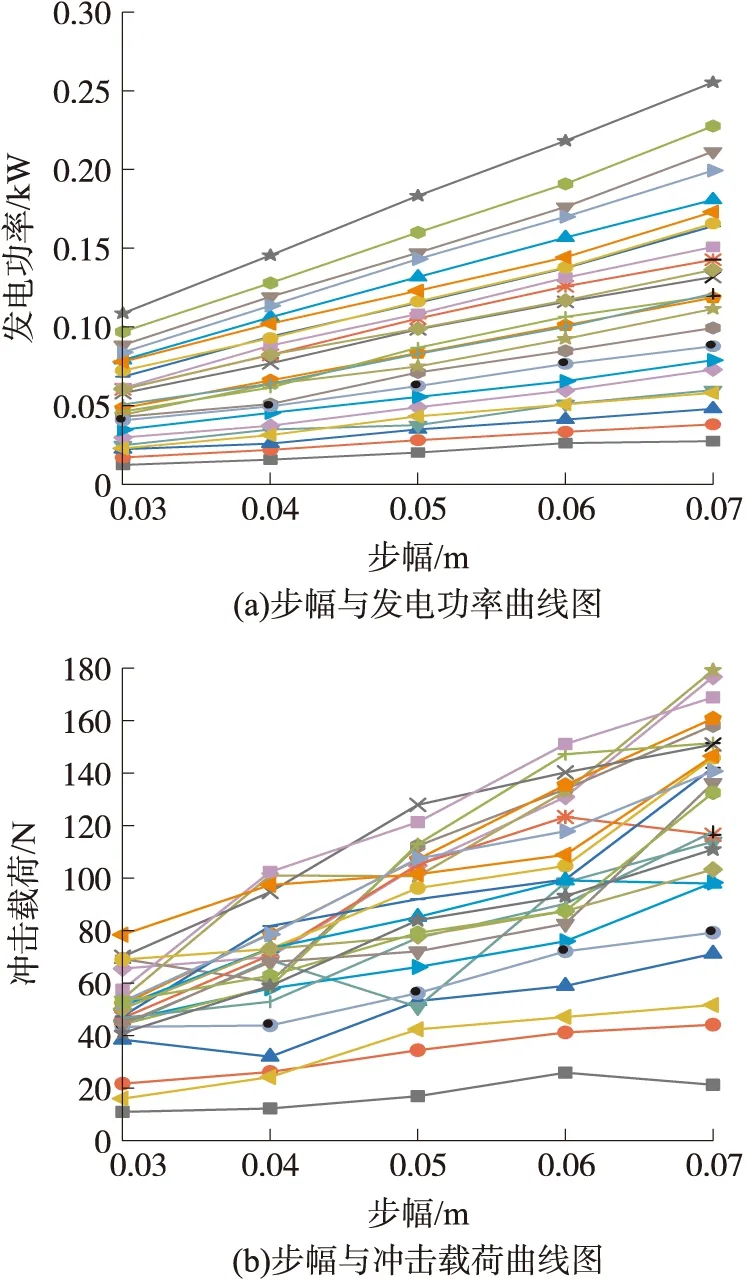
图8 不同步幅下的曲线图

采用Pearson相关性双尾检验的方法,对3个步态参数与背架性能进行了相关性分析,双变量相关性的分析结果见表3。可以看出:背负质量、步频、步幅与电功率、冲击载荷均成极显著正相关,背负质量与发电功率成强相关,步幅与冲击载荷成强相关,而步频与发电功率和冲击载荷成弱相关。

表3 步态参数与背架性能的相关性分析(n=125)

对于发电功率的影响排序:背负质量>步幅>步频,对人体冲击载荷的影响排序:步幅>步频>背负质量。

5 结论

本文针对自发电缓冲背架在不同步态下的控制策略问题,以自发电缓冲背架的发电功率和人体所受冲击载荷作为优化目标,采用NSGA-Ⅱ算法求解出最优前端Pareto解集,通过结合熵权法的加权广义马氏距离TOPSIS法,获得Pareto解集的最优解。

与使用传统优化方法相比,采用加权广义马氏距离TOPSIS法对发电缓冲背架综合性能优化具有较强的实用性。这是由于加权广义马氏距离,既解决了欧式距离的逆序和属性指标相关性的问题,又通过Moore-Penrose得到的广义逆矩阵,解决了传统马氏距离出现协防差矩阵不可逆的情形。熵权法获得属性指标的权重值,突出了决策中的客观性,避免了主观因素对决策过程的影响。利用相关性矩阵替换协方差矩阵,解决了由于协方差导致过于放大属性指标的影响。

下一步将基于本文提出的加权广义马氏距离TOPSIS法,获得多工况下的大样本最优方案,探索逐步回归法等近似回归方法,以获得发电缓冲背架的自适应控制模型。