基于自适应粒子群算法的增量配电网电源博弈规划

陆怀谷,刘绍东,张 渊,张 伟,张华成,严以臻,李亚杰,薛镕刚,陈 静

(1.国网江苏省电力有限公司常州供电公司,江苏 常州 213000;2.南京理工大学 自动化学院,江苏 南京 210094)

随着增量配电业务的不断开放,发电集团、社会资本、地方政府/园区政府等多种利益主体参与到增量配电网的建设中,运营方式以及资本环境也变得多样化。由于储能运营商、分布式电源(Distributed generation,DG)运营商等主体不断涌入增量配电市场,社会资本投资的增量配电业务可能与电网公司的规划出现重叠,导致并网规划容量过大、投资浪费、“弃风”、“弃光”等现象愈发严重[1-3],为提高能源利用率,应进行统一的市场规划,满足电力系统清洁高效的发展需求,合理解决各利益主体的投资诉求问题。

目前已有学者对增量配电网的规划展开一定研究。文献[4-6]为使配电网中发电资源和需求侧资源的互补特性得到充分发挥,从全局优化的角度建立多目标优化模型,以促进新能源消纳与成本优化,提高能源利用率,以此解决大规模多阶段电网规划遇到的问题;文献[7]通过考虑储能站的投资收益来对配电网进行规划,并将配电网优化规划问题转化为一个双层规划模型,分层实现储能投资商和配电网运营商的利益最大化。由于新能源技术的不断发展,多目标优化方法用于容量配置优化在建模上存在一定的局限性,过于依赖决策者的主观意愿,无法反映市场环境下各主体追求自身最大收益的过程。而相比较于传统的多目标优化方法,基于博弈论的优化理论在强调整体利益的同时,也关注个体利益,更加贴合于市场环境下各个参与主体利益冲突的场景。

目前,博弈论被广泛用于解决电力市场中多元主体间的交易决策和利益冲突问题[8]。文献[9]提出由粒子群算法迭代优化配电网动态孤岛划分博弈方法,建立博弈者的收益函数,通过博弈迭代得到不同孤岛时间下的孤岛划分策略;文献[10]以配电网综合运行成本为目标,结合博弈论与双层规划理论,建立主动配电网故障恢复模型,由混沌粒子群算法完成上下层优化,得到故障恢复方案。上述文献使用粒子群算法求解博弈问题,在一定程度上可以解决多主体之间的利益冲突问题,但粒子群算法在处理问题时容易陷入局部最优的情况,会影响最终策略的有效性和精确性。

为了充分考虑多元决策主体间的利益关系，本文提出了一种基于非合作博弈理论的方法来探讨增量配电网中各投资主体的规划方案，针对传统粒子群算法在寻优时容易陷入局部最优的问题，本文利用一种自适应粒子群算法，通过引入自适应权重系数，来提高粒子的全局搜索能力，规避决策过程中出现的局部最优情况。最后通过分析非博弈、基于传统粒子群算法的博弈和基于自适应粒子群算法的博弈等场景,对本文所提方法进行验证。

1 多元决策主体规划模型

1.1 多元决策主体的博弈关系

新电改革后电网公司负责保证电能传输质量、维护系统安全,仅收取相应的过网费,当增量配电网中电源投资主体的供电不足以满足负荷需求时向公共电网购电,因此本文主要对增量配电网中电源投资主体进行规划,选取DG投资运营商、储能运营商这两个主体进行仿真分析。与传统配电网由电网公司单独投资运营的规划问题不同,本文涉及两个电源投资主体且每个投资主体的利益诉求也不相同,在年预测负荷的基础上,结合市场机制构建各利益主体的规划模型,从个体利益出发对各个决策主体进行建设规划,避免新能源难以消纳、规划容量过大而投资浪费的问题,以最小的成本满足负荷用电需求,使整体收益实现最大化。

由图1可见,增量配电网中主要由DG为负荷供电,故DG投资运营商的决策变量为DG规划容量PDG。在增量配电网中增加储能环节,不仅可以促进新能源消纳,减少发电产能过剩,提高分布式发电的能源利用率,还可以增加削峰填谷,储能运营商决策变量为储能电池的规划容量PSE,可能影响DG的售电量。DG投资运营商、储能运营商各自为政,决策变量相互影响,形成博弈关系。

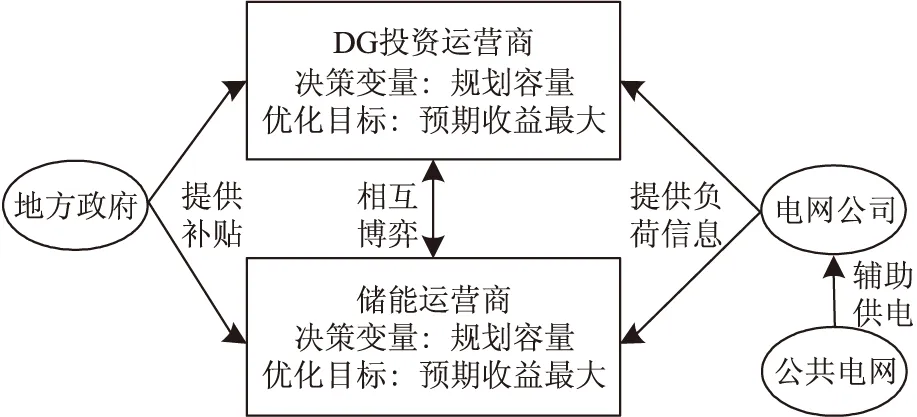
图1 多元决策主体的博弈关系

1.2 各主体预期收益模型

在此博弈模式下,本文基于全寿命周期的理念,考虑资金贴现率,采用年平均收入和成本计算各主体的预期收益,在计算过程中采用时间序列模型确定DG、储能电池和负荷的特性,具体收益模型如下。

1.2.1 DG投资运营商

(1)

(2)

(3)

(4)

1.2.2 储能运营商

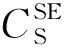
(5)

式中

(6)

(7)

(8)

(9)

(10)

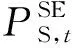
2 非合作博弈规划模型

2.1 非合作博弈模型

以综合考虑DG运营商、储能运营商两个利益主体,分析各市场主体对增量配电网规划建设进行决策时的关系。根据非合作博弈理论构建规划模型,DG投资运营商和储能运营商在相同的环境下做出各自的策略选择PDG和PSE,在博弈过程中根据自身能力与所掌握的信息独立决策规划。具体的非合作博弈模型如下所述:

(1)参与者集合N={DG,SE}

(2)策略集合Ω={PDG,PSE}

(3)收益函数CDG(PDG,PSE),CSE(PDG,PSE)

(11)

(12)

2.2 约束条件

(1)DG单元投入使用后,DG单元需满足一定的出力约束以及规划建设的容量约束

(13)

PDG,min≤PDG≤PDG,max

(14)

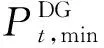
(2)储能电池的充放电功率需要满足限制,储能的荷电状态也需满足一定的要求

(15)

SOCmin≤SOC(t)≤SOCmax

(16)

对于衰退期企业，其产品市场开始萎缩，企业盈利能力大幅下降，外部投资者的关注重点是企业的生存能力和债务清偿能力，而无暇顾及企业的碳信息披露情况，此时企业若选择过度进行碳信息披露，不但无法使其摆脱经营困境，还会造成企业不必要的人力投入和财务负担，加大企业获取外部融资的难度。据此，提出假设5。

3 基于非合作博弈的增量配电网电源规划模型求解

3.1 自适应粒子群算法

非合作博弈是多个参与者独立优化各自目标的耦合问题,是一种较复杂的非统一优化问题,处理这类问题通常使用遗传算法、粒子群算法等。其中,粒子群算法相比其他智能算法效率更高,收敛速度更快。目前在求解博弈均衡解时通常可采用迭代搜索法、最大—最小优化法和剔除劣势策略法等。故而将粒子群算法与迭代搜索法相结合,使粒子群从随机解出发通过每次迭代,不断更新自身的速度和位置,最终达到一个收敛的稳定解,有更好的全局收敛性。

传统粒子群算法在处理DG和储能容量规划问题时,由于算法结构简单,在运行过程中粒子群容易早熟而陷入局部最优[11]。为了避免粒子早熟,使粒子群具有较好的全局搜索能力,需选取合适的惯性权重系数,故本文引入自适应惯性权重系数ω,粒子群在每次迭代后,各个粒子根据自身所对应的适应度值,即目标函数值进行自适应更新,具体为

(17)

式中:ωmax和ωmin分别为选取的最大和最小权重系数,Ci是粒子i的函数值,Cavg和Cmin分别为粒子群函数的平均值和最小值。

设定粒子群在一个N维空间进行搜索,粒子i在第m次迭代后的位置和速度用两个N维向量来表示,分别为xi=(xi1,xi2,…,xiN)T、vi=(vi1,vi2,…,viN)T,i=1,2,…,m,第m+1次迭代后的速度和位置更新为

(18)

(19)

图2 自适应粒子群算法流程

3.2 增量配电网电源博弈规划模型求解

通过自适应粒子群算法求解每一轮的最优组合,输出达到Nash均衡的最优策略,图3为博弈规划求解流程图。

图3 博弈规划求解流程图

图3具体的求解步骤如下。

步骤1初始化粒子位置和速度,设置技术经济数据,包括预测负荷、电价、风速、资金贴现率等;

步骤2建立非合作博弈模型,生成博弈的策略空间;

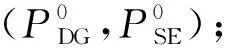
(20)

(21)

步骤5判断前后两次迭代得到的结果是否相同,若相同,即

(22)

此结果就是Nash均衡点,继续往下执行,否则,返回到步骤4继续优化。

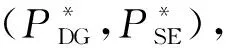
4 仿真及结果分析

4.1 模型参数

选取某110 kV增量配电网试点区域为仿真分析的算例,年度负荷时间序列取自IEEE-RTS的标准负荷数据[12],峰荷为10 MW。通过求解Nash均衡确定DG运营商和储能运营商的最优规划方案。DG考虑为风力发电,DG和储能电池的相关技术经济参数分别如表1、表2所示。

表1 DG技术经济参数

表2 储能技术经济参数

4.2 结果分析

4.2.1 规划结果

基于由DG运营商与储能运营商所建立的相互博弈的格局,为了对比分析基于自适应粒子群的投资博弈对增量配电网电源规划的影响,验证文中提出方法的合理性与优越性,分别设置3种场景,见表3。

为进一步说明基于自适应粒子群的投资博弈对增量配电网电源规划的必要性,对3种场景下各主体收益以及容量规划进行分析,规划结果分别如表3及图4和5所示。

表3 规划结果

图4 不同场景下的容量规划

从图4可以看出,在场景1下,DG运营商和储能运营商的规划容量分别为8 013 kW,4 826 kW;在场景2下,DG运营商和储能运营商的规划容量分别为9 621 kW,4 943 kW;在场景3下,DG运营商和储能运营商的规划容量分别为9 847 kW,4 991 kW。相对于场景2和场景3,场景1中DG的规划容量比较小,因为没有充分考虑两个决策主体的利益结构,分析多主体之间的利益关系,只是相互独立、各自规划,仅通过权重比把二者联系起来,新能源的消纳率较低,DG能源利用率不高,没有充分发挥作用。场景2和场景3的规划值比较接近,原因在于这两种场景都充分挖掘了两个主体之间内在的利益博弈关系,能够减少“弃风”现象,充分发挥DG的作用,使得规划容量明显增大。

从图5可以看出,在场景1下,DG和储能运营商的利润分别是180.77万元,55.19万元;在场景2下,DG和储能运营商的利润分别是539.5万元,123.6万元;在场景3下,DG和储能运营商的利润分别是573.36万元,142.43万元。通过比较发现,场景2和场景3下的DG运营商和储能运营商的收益值都要明显高于场景1下的收益值,因为场景1忽略了DG运营商和储能运营商之间的利益博弈关系,只针对单一主体进行增量配电网电源规划,忽视了不同主体投资的增量配电业务可能出现的重叠现象,导致并网规划容量过大,容易造成资源的浪费,不利于推动整体的经济效益向最优方向发展。场景2和场景3的DG运营商和储能运营商的收益值虽然相差不大,但由于场景2采用的是传统粒子群算法,无法动态地调节搜索速度,可能出现局部最优的情况,整体性能不够优越。场景3在此基础上进行了一定改进,采用基于自适应的粒子群算法,在寻优时不易出现由于局部最优而无法找到整体最优解的问题,因此场景3得到的收益最优解比场景2得到的解更好,经济性更为突出。

图5 不同场景下的收益值

4.2.2 比较分析

(1)验证博弈优势

为说明投资博弈相对于非投资博弈对增量配电网电源规划更具优势,对这两种场景下的多主体收益和容量进行比较分析。参考历史数据和实际需求,DG运营商和储能运营商各自收益按权重比进行分配,权重系数设为0.8∶0.2。

通过分析图6-8可知,在非博弈规划下,系统总收益为235.6万元,风机的规划容量为8 013 kW,储能的规划容量为4 826 kW。在博弈规划下,系统总收益为663.1万元,风机的规划容量为9 621 kW,储能的规划容量为4 943 kW。博弈规划方法下的收敛速度要明显快于传统规划方法下的收敛速度,计算求解的效率更高;其总收益值也远远大于传统规划的总收益。传统规划方法下的风机装机容量远远比不上博弈规划下的风机装机容量,没有做到可再生资源的充分利用。综合比较来看,博弈规划方法明显优于传统的规划方法,有利于市场整体获得最大收益,提高能源利用率。

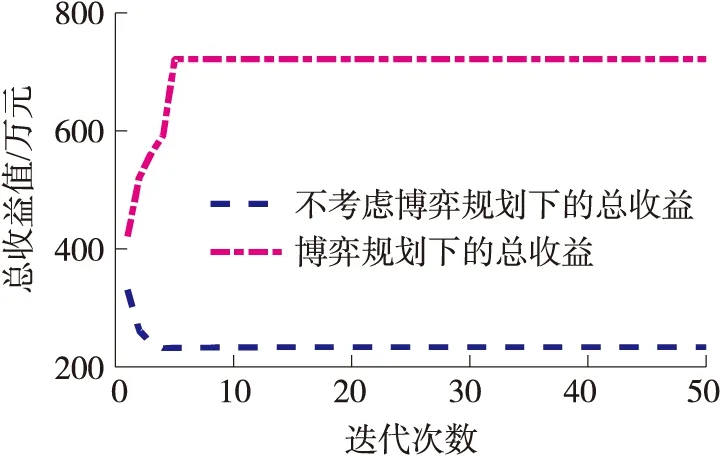
图6 总收益变化图

(2)验证自适应粒子群优势

为进一步说明自适应粒子群算法相比较传统的粒子群算法在全局寻优上的优势,对这两种算法进行比较分析。在自适应粒子群博弈规划下,系统总收益为715.79万元,风机的规划容量为9 847 kW,储能的规划容量为4 991 kW。采用两种粒子群算法求解,DG运营商和储能运营商的具体收益结果分别如图9和10所示。

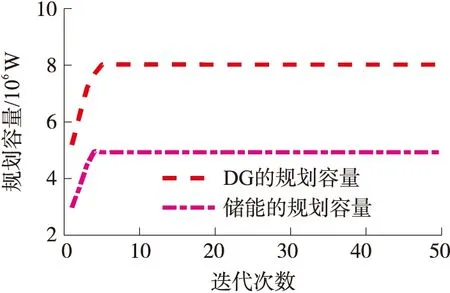
图7 非博弈规划下的设备容量变化图

图8 博弈规划下的设备容量变化图

图9 DG运营商的收益值和成本值

图10 储能运营商的收益值和成本值

针对DG和储能运营商,两种算法求解出的年运行维护费用和年投资费用差别不大,但自适应粒子群得出的年售电收入明显高于传统粒子群算法计算出的数值,因此总收益值更高。从储能运营商角度分析可知,年投资成本和年运行维护成本差别不大,在自适应粒子群算法下,在年售电收入和辅助服务收入方面优势显著,此算法下的总收益值同样更高。

综上所述,在求解系统最优利益值方面,自适应粒子群算法相对于传统的粒子群算法更有优势,更容易得到全局最优解,有利于提高整体经济效益,更好地增强增量配电网市场的活跃性。

5 结论

本文利用自适应粒子群算法和非合作博弈理论方法，研究了增量配电网电源侧的规划方案，通过对不同场景对比分析，证实了本文所提方法的有效性，结果表明其具有以下3个优势：(1)基于非合作博弈理论，使多主体在博弈过程中不断优化自身策略，实现DG和储能的合理配置，避免了资源浪费；(2)将传统粒子群算法与自适应粒子群算法进行比较分析，验证了基于自适应粒子群算法能够全局寻优的优越性能；(3)所提方法模拟了市场中DG运营商和储能运营商的博弈行为，合理配置DG和储能容量，提高能源利用率，避免资源浪费，提升了增量配电网市场的活跃性，促进了增量配电网的持续健康发展。