面板数据分位数回归模型的三阶段估计
2021-05-27邹灵,吴媛
邹 灵,吴 媛
(西南交通大学希望学院 商学院,四川 成都 610400)
面板数据分析方法是当前热点的统计分析方法之一,但传统的面板数据分析方法对数据分布要求过高,实际数据往往不满足其数据分布前提。针对该类问题,建议采用分位数回归的方法。1978年,Koenker和Basset[1]提出了分位数回归(NQR)的方法。2004年Koenker[2]首次将分位数回归的方法应用于纵向数据的分析中。且在实际问题分析中,数据的内生性问题会导致模型产生误差,如在研究外商投资(FDI)对环境污染的影响时,FDI作为解释变量存在内生性,为解决FDI的内生性问题,贺培等[3]采用两阶段最小二乘法(2SLS)建立相关模型;朱平芳等[4]却使用工具变量建立分位数回归模型。针对含有内生变量的面板模型,李劭珉等[5]在消除个体效应项之后引入工具变量,建立了面板数据分位数回归模型;邹灵等[6]引入工具变量解决模型的内生性问题后再消除个体效应项,提出了面板数据分位数回归模型的工具变量估计方法(IVQR)。本文将基于改进的两阶段分位数回归和面板数据分位数回归模型的工具变量估计方法,针对含有内生变量的面板数据,提出面板数据分位数回归的三阶段估计(TQR),并对该方法进行模拟研究。
本文首先引入工具变量消除模型的内生性,然后利用复合分位数回归估计出个体效应,最后使用分位数回归得到参数的估计。接着对Naive最小二乘估计(NLS)、NQR、2SLS、IVQR和TQR进行模拟研究,比较五种方法在不同分布下的估计效果。
1.面板数据的分位数回归模型的工具变量估计
讨论如下面板数据模型:


2.模拟研究
本节通过模拟对所提的三阶段估计方法的有限样本性质进行研究,模拟时分别取50、100的样本量,重复实验次数1000次。考虑如下含有内生变量面板数据模型:

从表1可以看出,无论误差项是服从何种分布时,NLS和NQR0.5对θ的估计都有较大的误差,这是因为Navie估计未消除变量的内生性,从而导致所得的估计存在较大的误差。2SLS在误差项服从正态分布时,对参数有较好的估计,但当误差项服从非正态分布时,所得估计的Bias和SD都较大。IVQR0.5和TQR0.5两种估计方法无论在何种分布下都有较好的估计效果,但是TQR0.5方法的估计结果的Bias和SD都比IVQR0.5方法小,并且随着样本量的增加,TQR0.5的偏差和标准差却在变小。本文所提方法不仅巧妙的估计出个体效应项,还处理了模型的内生问题,并且所得估计不受模型误差分布的影响。
为了验证三阶段估计方法的渐近正态性质,下面给出了不同误差分布情形下,样本量为100时各参数的QQ图。

表1 五种方法下的参数估计的偏差与标准差
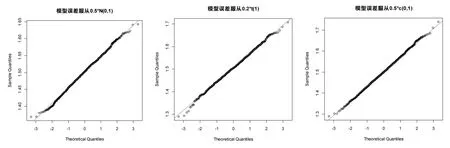
图1 参数θ在不同分布下的QQ图

图2 参数β在不同分布下的QQ图
从图1和图2可以看出,图上的点近似在一条直线。因此,所提出的TQR0.5具有渐近正态性。
3.结语
本文针对含有内生变量的面板数据,提出TQR的回归方法。首先通过最小二乘法消除解释变量的内生性,然后通过复合分位数回归估计出个体效应项,最后使用分位数回归得到参数估计。进一步通过模拟研究证实了该方法的有限样本性质。本文所提方法不仅巧妙的估计出了个体效应项,还有效地解决了模型的内生性问题。
