基于蚁群聚类的不平衡数据过采样方法
2021-05-27刘其成牟春晓
高 阳,刘其成,牟春晓
(烟台大学计算机与控制工程学院,山东 烟台 264005)
不平衡数据集是指样本集中各自类别所含样本数目的多少存在较大的差距,对于含有较多样本数的类别称之为多数类(反例)样本,反之为少数类(正例)样本[1]。在不平衡数据集中,样本数量较少的类可能包含更加关键的信息。例如医疗诊断中人类患肿瘤性疾病的事件属于少数类,但是如果将肿瘤性疾病误诊为没有病变,可能就会丧失早期治疗的机会,造成难以挽回的结果[2]。不平衡分类产生的原因是采用普通分类方法去处理不平衡数据集导致分类器的分类结果不理想[3]。例如一个数据集中有998个反例,2个正例,那么只需要选择一个将训练集数据预测为反例的学习方法即可,这样该学习方法生成的学习器就可以达到99.8%的分类精度。但这样的学习器对不平衡数据集的研究起不到任何积极的作用,因为它往往是预测不出正例的。随着大数据时代的到来,现在这种问题普遍存在于故障检测、信用卡欺诈检测、网络入侵识别以及电子邮件分类等领域,因此如何将不均衡的数据集既快速又准确的处理是当下学术研究的一个热门方向[4-7]。
通常从算法和数据2个层面解决不平衡数据集问题[8]。数据层面有2种选择,分别是增大正例样本数目的过采样以及缩减反例样本数目的欠采样。二者有一定的共同之处,都是通过改变各自类别的样本数目使数据集达到一定程度的平衡。代表性的算法有合成少数类过采样技术SMOTE[9]。算法层面所用到的方法,主要是在得到平衡数据集之后,通过引入代价矩阵或者对分类错误率进行改进。将数据层面的方法和算法层面的方法结合起来得到的新分类器可以具有更强的多元性和鲁棒性。
传统分类器将不平衡数据集中的少数类预测正确的精度很低,为此对于上文提到的2种解决方案,当前研究者大都以增加数据集中的正例样本数目为切入点。文献[9]所用的SMOTE算法是针对所有的正例样本过采样,容易产生重叠的新合成的正例样本。Safe-level SMOTE[10]算法会对每个少数类样本的检测其临近同类样本的个数,并以此设置每个少数类样本的安全等级,当其值高于一定阈值时才会对此样本进行过采样。该方法在一定程度上避免了噪声数据的产生,但合成数据都过于集中在少数类内部可能会出现过拟合现象。DB-SMOTE算法[11]以正例子簇簇心的距离为标准进行过采样,挑选那些边际处的正例样本当作种子,以此避免过拟合现象,但这种方法容易产生重叠样例。WOHC算法[12]考虑到在过采样时会产生重叠样本以及导致过拟合问题,采用加权过采样的方法避免产生重叠样本,但是该方法只能起到预防的作用,并不能起到根除产生重叠样本的作用。
对于上述问题,本文提出基于蚁群聚类改进的SMOTE不平衡数据过采样算法ACC-SMOTE(Ant Colony Clustering Synthetic Minority Oversampling Technique)。首先采用改善的蚁群聚类算法将正例样本划分为不同的子簇,而后再根据各个正例子簇所占的样本比例采用SMOTE算法来过采样;最后让经过上述操作的正例样本采用Tomek Links方法及时改正,清理掉正例样本集中产生的噪声数据,进而提高合成之后正例样本的质量。本文提出的ACC-SMOTE算法与经典的SMOTE[9]、Safe-leve SMOTE[10]、DB-SMOTE[11]、WOHC[12]算法相对比,实验结果显示该方法使正例样本的预测精准度得到提升。
1 预备理论
1.1 SMOTE算法
CHAWLA等[9]在2002年提出了对正例样本合成的方法,即SMOTE。首先随机选择一个正例样本,然后再找出距离它最近的k个样本,按照采样概率从距离它最近的k个样本中选择一个样本按照公式(1)合成新样本,反复执行以上过程使数据集达到平衡。
Y=X1+rand·(X1-X2)。
(1)
其中,X1正例样本,X2是距离X1最近的k个样本中的一个,rand是随机生成一个从0至1区间内的数的函数,Y代表了新生成的正例样本。
1.2 蚁群算法基本原理
蚁群聚类算法的思想是让蚂蚁在一个含有许多数据的区域随机挪动转移[13]。当蚂蚁随机挪动到其中一个带有数据的区域时,计算该数据在它领域内的相似度来得到蚂蚁背负它的概率,如果该概率比随机数大,蚂蚁捡起该数据并背负它随机挪动转移,否则蚂蚁不捡起该数据继续随机挪动转移;在蚂蚁背负数据随机挪动转移到不含数据的空白区域时,计算空白区域的相似度得到丢弃该数据的概率,若概率值大于随机数则丢弃,反之丢弃失败,继续挪动转移到别的空白区域判断。蚁群经过上述过程反复的捡起、挪动转移、丢弃当达到某个循环结束标志时就会得到一个最终的聚类结果。
1.3 Tomek Link数据清理技术
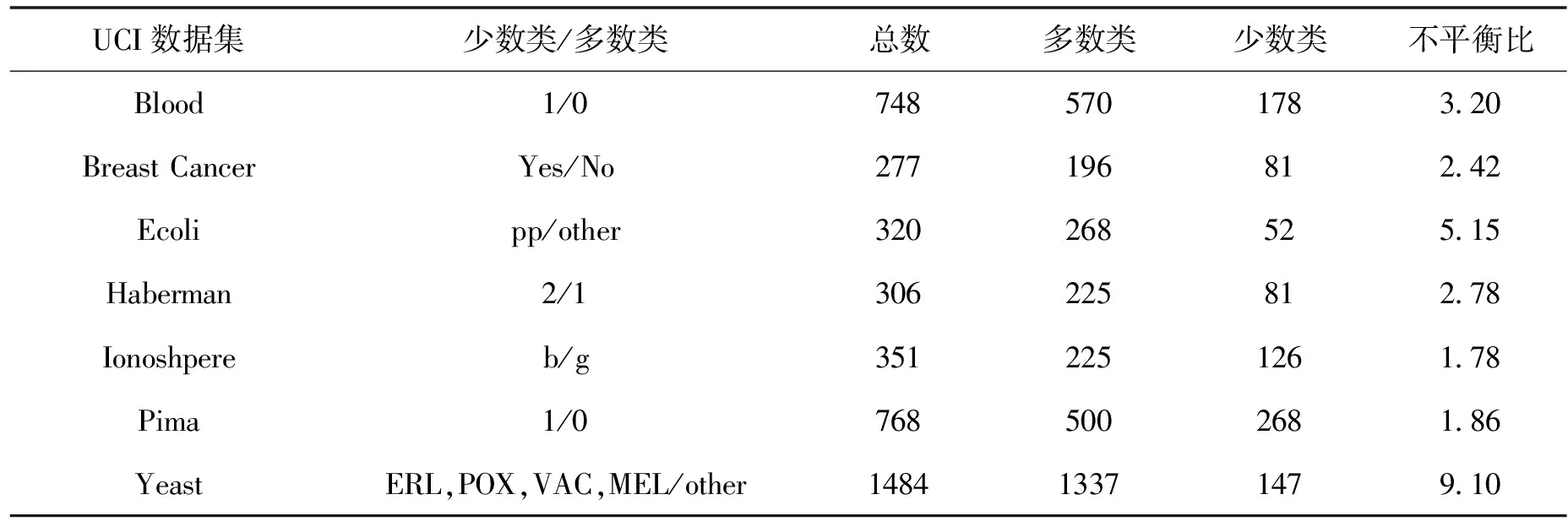
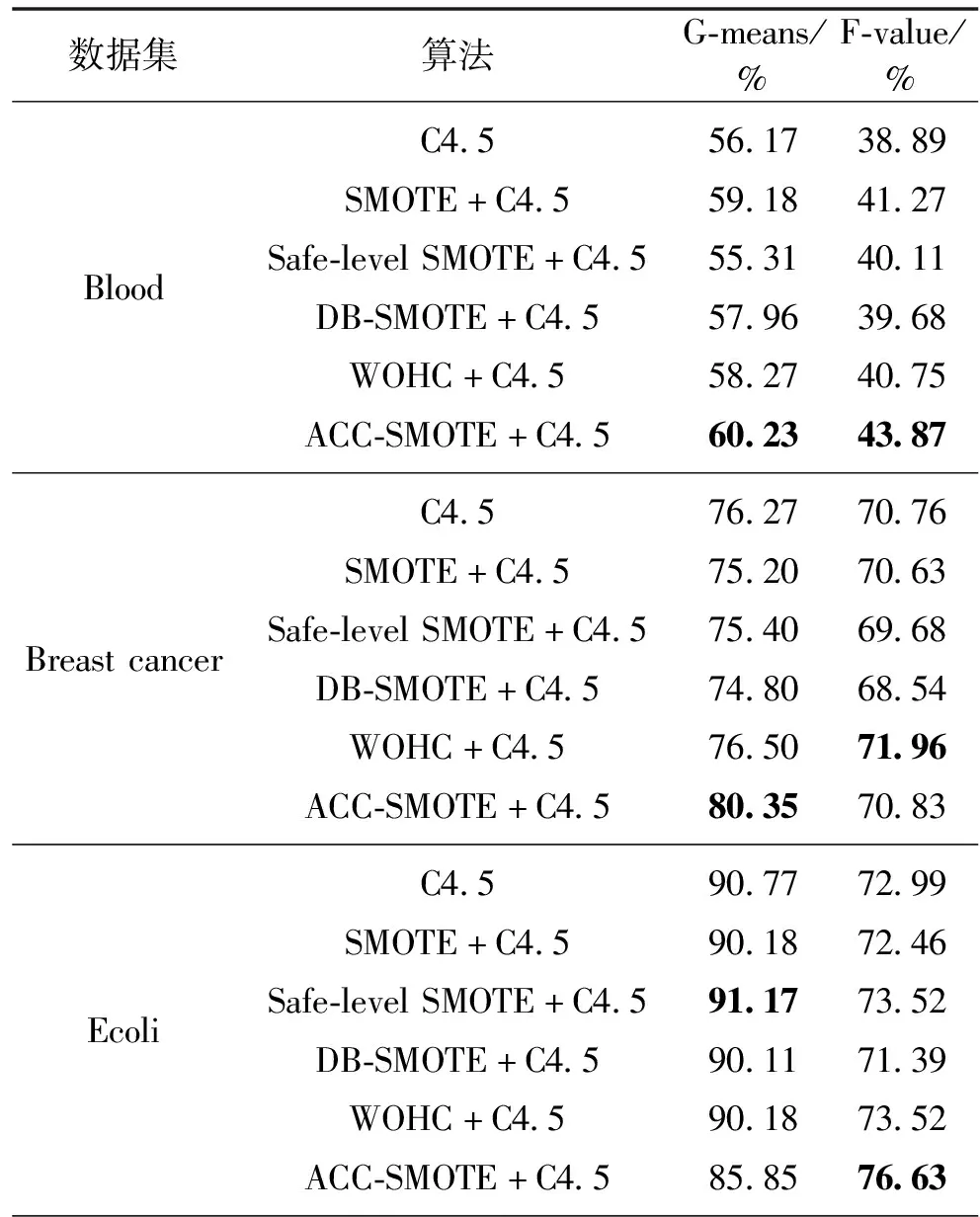
Tomek Links是对数据集清理的一种关键技术,可以用它来清理那些因过采样而产生的噪声数据和重叠样例[14]。其主要思想是将Tomek Links看作是1对数据实例,它们距离(欧式距离)很近但属于不同的类别。只有当2个数据实例中的1个是噪声数据或者2个数据实例都在各自类别的边界上时,这2个数据实例才有可能构成一对Tomek Links。比如给定1对数据(xi,xj),xi,xj属于不同的类别,即少数类xi,多数类xj,用d(xi,xj)表示它们之间的欧式距离。如果不存在另一数据实例x,使得d(xi,x) 为了获取更多数据集中正例样本所表示的信息内容,本文通过致力于改进SMOTE过采样算法得到ACC-SMOTE算法,使各自类别的样本数目达到相对均衡。该算法不仅着眼于数据集不同类别之间的不平衡,还想到同类之间不同子簇所含样本数目的差异以及噪声数据对样本的影响。采用蚁群聚类得到最优解,为下一阶段采用SMOTE算法过采样合成样本提供更准确的聚类结果,从而得到更理想的合成样本。为了根除合成新样本产生的重叠样本,该算法采用了Tomek Links方法。ACC-SMOTE算法主要分为三部分:蚁群聚类阶段,过采样阶段,合成数据整理阶段。 在ACC-SMOTE算法的初始阶段,需要将训练集先进行预处理操作,即将训练集中的少数类进行聚类,分为不同的子簇,然后再根据其所占的比例进行过采样。这样做的目的是着眼于数据集不同类别之间的不平衡而且还有同类之间不同子簇所含样本数目的差异,从而保证合成样本的质量,防止过拟合。 为避免一个数据反复地被拾起放下,导致聚类速度变慢,同时也为了避免因为随机性导致聚类结果的准确性降低,ACC-SMOTE算法采用的蚁群聚类方法每只蚂蚁对应一种聚类方案,转移方程中只有信息素权重。这是因为每个簇的聚类中心需要不断地移动,转移期望不好衡量,所以转移方程中没有转移期望。在搜索解空间选择某个点的类别时,将信息素看成当前点与每个类别的临近程度,以概率p挑选信息素最高的点,1-p的概率按信息素分布用轮盘赌方法挑选。概率p计算公式如下: (2) 式(2)中1-pTh的值表示蚂蚁在搜索路径中随机因素作用的强度,其值越大,选择走过路径的概率越大,从而导致局部最优,因此将直接转移阈值设为pTh=0.9;τij(t)表达的意思是时间为t时,边(i,j)上所含的信息素。 更新信息素方面,为了解决其更新缺乏时效性的问题,根据方案的优度(1/MSE)来增加方案上所有点-类对的信息素,每次迭代,每只蚂蚁都得到一个方案;然后刷新每个点-类对上的信息素的浓度值。具体公式如下,其中所有方案已按MSE升序排好。 τij(t+m)=(1-volR)·τij(t)+Δτij(t), (3) (4) (5) 式(3)中考虑到信息正反馈的作用,volR较小时,信息正反馈占主导地位,算法收敛速度加快。为了提高蚁群聚类算法的收敛速度,可将信息素的散发率适当降低为volR=0.1,式(4)中刷新信息素的最优方案数updNum=3,式(5)中信息素系数pherC=107,最优方案MSE的数组为sol数组。 上述算法的伪代码如下: 输入:聚类数K,样本数N,少数类mindata 输出:K个少数类子簇 (1)每只蚂蚁对应一种解决方案。 (2)初始化,生成一个较好的聚类方案,让所有蚂蚁都从该方案出发。 (3)将信息素看成当前点与每个类别的临近程度,根据公式(2)搜索解空间。 (4)依靠公式(3)(4)(5)刷新信息素;依靠方案的优度来增加方案中所有点类对的信息素。 (5)反复执行步骤(2)(3)(4),直到Num大于MaxNum或方案连续CRN次重复并且Num大于MinNum,结束循环(Num表示目前执行了循环多少次,MaxNum和MinNum分别代表最多和最少可以执行循环多少次)。 对于步骤(1)(2)使用最近距离轮盘赌法,在给定的N个正例样本中选择较分散的K个数据样本当成初始的子簇中心,按最近距离给出初始的聚类方案,存到每只的solution数组中;然后让所有蚂蚁都从该聚类方案出发。步骤(4)的更新过程中,将会失去volR比例的信息素,MSE较小的updNum个方案对其点-类对的信息素产生增量。 经过上述改进的蚁群聚类可以得到不同少数类的子簇,其中2.1节的4个公式是该算法的核心,直接决定了聚类结果的好坏。采用SMOTE算法对少数类进行过采样大致可分为以下2个部分,首先将少数类划分为不同的子簇,根据每个子簇大小所占样本的比例确定采样比重T,如公式(6)。然后按照公式(1)对不同子簇的少数类进行过采样,重复执行以上过程直到达到过采样比重。SMOTE算法可以使正例样本数目增加,进而改善数据集的不平衡性。 Ti=(Nmax-Nmin)×(Nmin-Ci)/Nmin。 (6) 式(6)中Nmax,Nmin分别代表反例以及正例的样本数目;Ci表示当前子簇的样本数目;Ti代表i子簇的采样比重。 单个正例样本簇实现SMOTE过采样的伪代码如下。 输入:正例样本簇mindata,反例样本数m1,正例样本数m2 输出:合成样本后新的正例样本簇new-mindata (1)[r1,c1]=size(mindata); (2)//确定采样比例 (3)T=(m2-m1)×(m1-r1)/m1;//计算过采样之后的簇样本数 (4)ratio=T./r1;//使用每个样本的KNN次数 (5)k=5;//近邻数 (6)new-mindata=mySMOTE(mindata,ratio,k); (7)//调用另个函数中SMOTE算法根据公式(1)过采样 (8)[r2,c2]=size(new-mindata); (9)ifr2>T (10)new=randperm(r2,T); (11)new-mindata=new-mindata(new,:); (12)else (13)new=randperm(r2,T-r2); (15)end if 样本合成示例如图1。 图1 过采样合成样本示例 普通情况下在合成新的少数类样本时产生噪声样本是不可消除的,而且噪声样本的存在会使分类器的性能下降。况且对少数类来说,样本数目少就导致了它本身抗噪声能力弱的缺陷,从而噪声数据对分类效果产生较大的影响。通过过采样对少数类样本合成,从而使得样本集中各类样本数相对平衡。如果在过采样时种子样本的近邻样本是多数类样本,那么合成之后的样本就会是噪声数据,在使用分类器进行分类时就不会提供有用的信息,反而可能会误导分类器做出错误的判断,进而会降低其分类精度。因此ACC-SMOTE算法采用Tomek Links数据清理技术处理新合成的样本,其思想已在1.3节有简单介绍,下面主要给出Tomek Links算法实现的伪代码。 输入:原始数据集Originaldata,数据的维度ic 输出:Cleardata (1)min-dist=zeros(size(Originaldata,1), 1); (2)tomek-link=[]; 5)回喷入炉工艺。发达国家垃圾热值高,含水率低,且实行垃圾分类收集处理的方式,所以发达国家垃圾渗沥液产生量小,可直接回喷入炉燃烧,解决了渗沥液浓液的二次污染问题[1]。但我国生活垃圾没有分选,生活垃圾中厨余垃圾占比大,含水率高,渗沥液及处理后的浓缩液产生量大[2]。若全部回喷入炉,将降低炉温,造成燃烧负荷波动大,甚至850℃、2 s无法保证,且减少锅炉的蒸发量和整个电厂发电量[3-4]。 (3)fori=1: size(Originaldata, 1) (4)sample-mat=repmat(Originaldata(i,1:ic-1), (5)size((Originaldata,1), 1); (6)dists=sum(abs(Originaldata(:,1:ic-1)-sample-mat), 2); (7)[ds,id]=sort(dists); (8)if Originaldata(id(2),ic)~=Originaldata(i,ic) (9)min-dist(i)=id(2); (10)if min-dist(id(2))==i (11)if Originaldata(i,ic)==0 (12)tomek-link=[tomek-linki]; (13)else (14)tomek-link=[tomek-linkid(2)]; (15) end if (16) end if (17) end if (18) end for (19)Originaldata(tomek-link,:)=[]; (20)Cleardata=Originaldata; (21)Output Cleardata 实验过程将分别对多组UCI数据集采取二八分原则将数据集分为测试集以及训练集[15],用上述方法来验证算法的有效性以及可行性。由于实验中数据集的划分以及合成新样本时存在偶然性,因此下面的结果都是执行多次取得的平均值。 对于不平衡数据集,传统的分类结果精准度和评价指标已不适用,为此采用从如表1所示的混淆矩阵中得到新评价指标G-means[16]和F-value[17]。 表1 混淆矩阵 根据表1可以得到如下所示的评价指标: 正类样本召回率: (7) 负类样本召回率: (8) 正类样本查准率: (9) G-means值: (10) F-value值: (11) G-means值综合考量正例样本和反例样本的召回率,只有当两者值都大时,G-means值才会大,可以更精确地显示出模型的分类效果。而F-value值着眼于对正例样本的查准率和召回率,可以更加精确地显示出正例样本的分类准确度。由此本文实验将由G-means值和F-value值作为评价模型的指标。 在实验之前,对一些数据进行整合,主要包括删除有属性缺失的数据和将多分类转变成二分类。数据集结构如表2。 表2 UCI数据集 为了证明ACC-SMOTE算法的有效性及可行性,在Blood、Breast cancer、Ecoli、Haberman、Ionoshpere、Pima、Yeast 7种不同的数据集里将SMOTE[9]、Safe-level SMOTE[10]、DB-SMOTE[11]、WOHC[12]4种算法分别结合C4.5分类算法作比较,采用G-means和F-value作为评价指标。把不结合任何过采样算法的C4.5的分类结果作为比较准则,从实验结果说明了处理不平衡数据的重要性。实验结果如表3。 从表3中可以得出在数据集Blood,Haberman,Ionoshpere,Pima,Yeast中,ACC-SMOTE算法的G-means值和F-value值均高于其他算法,G-means值在Blood,Breast cancer,Haberman,Ionoshpere 4组数据集上也取得较好效果。该算法相比于WOHC算法G-means和F-value值均有提升,一方面该算法有效克服了噪声样本的影响,另一方面,该算法能够较好的处理具有分类困难样本的不平衡数据,有效的明确正例样本的边界,进而提高了分类的精度。 表3 ACC-SMOTE算法与其他算法的比较 对于不平衡数据集问题,现在已有的方法大都仅仅着眼于数据集不同类别之间的不平衡,没有考虑到同类之间不同子簇所含样本数目的差异,经过过采样之后的训练集可能会出现边缘化问题,训练出的模型更可能出现过拟合现象,从而降低分类精准度。为了克服现有过采样算法的不足,提出了ACC-SMOTE算法。该算法针对合成新样本过程存在的问题,引入聚类思想和数据清理技术,有效降低了数据集中类间、类内的不平衡性以及边缘化问题出现的概率。经验证ACC-SMOTE算法可以明显提高少数类样本的分类准确度,分类性能更优,从而证明了该算法的可行性与有效性。 现实生活中还会出现多分类的情形,以后的工作可以进一步将多分类数据集的采样方法作为研究内容,以便于将ACC-SMOTE算法应用于更多领域。2 改进的过采样算法ACC-SMOTE
2.1 蚁群聚类阶段

2.2 过采样阶段
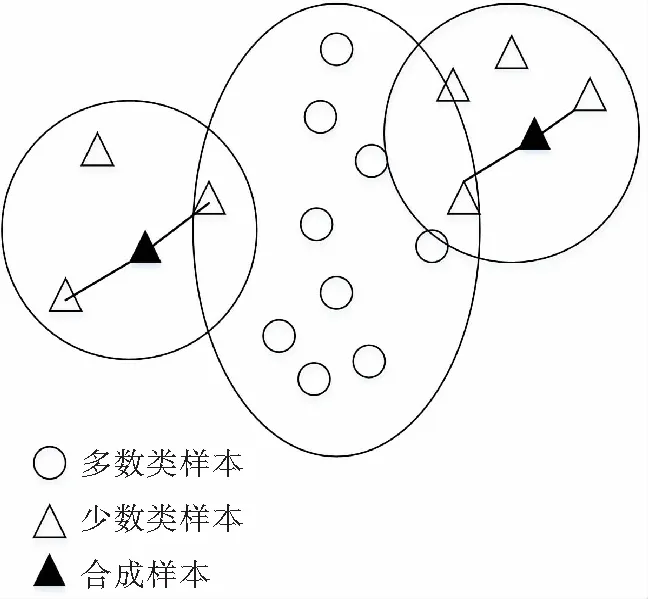
2.3 合成数据整理阶段
3 实验结果分析
3.1 评价指标

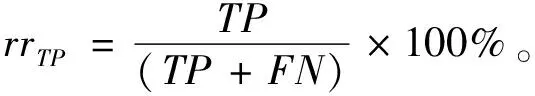
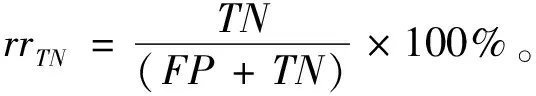
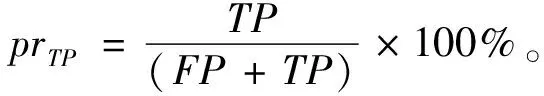
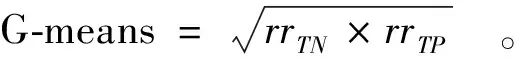
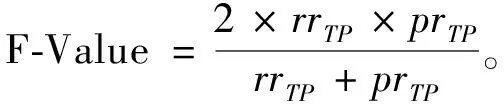
3.2 实验数据
3.3 实验结果对比
4 结 语
