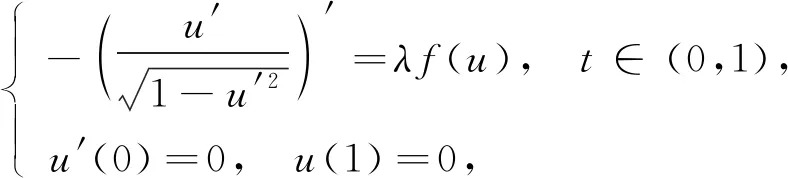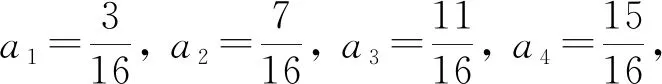Minkowski空间一维给定平均曲率型方程Robin问题正解的存在性和多解性
2021-05-26苗亮英何志乾
苗亮英, 何志乾
(1. 青海民族大学 数学与统计学院, 西宁 810007; 2. 青海大学 基础课教学研究部, 西宁 810016)
正解的存在性和多解性, 得到了非线性项f的零点个数与该Robin问题正解个数的关系. 其中: λ是正参数; a∈C[0,1]; f∈C([0,∞),[0,∞))满足存在两个正的点列ai,bi(i=1,2,…,n), ai
0 引 言
Minkowski空间中给定平均曲率方程在微分几何和广义相对论中有重要应用, 例如: 相对论状态下的质点运动状态研究[1]及非线性电动力学理论中的Born-Infeld模型[2-3]等. 目前, 关于其正解的存在性和多解性研究已取得了许多结果[4-10]. Coelho等[4]研究了一维Minkowski空间给定平均曲率型方程Dirichlet问题

(1)
正解的存在性和多解性, 其中f是一个Lp-Carathéodory函数, 用变分法和拓扑度方法得到了问题(1)至少存在1个、 2个、 3个正解; Zhang等[5]用时间映像分析法证明了一维给定平均曲率型方程Robin问题
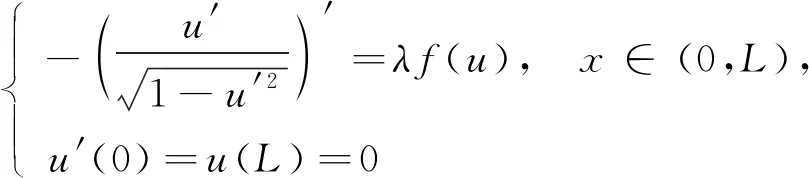
(2)
正解的精确个数, 其中λ是正参数,f(s)=sp, 0 (3) 正解的存在性与多解性, 其中λ是正参数,a∈C[0,1],f∈C([0,∞),[0,∞)). 由于问题(3)是非自治问题, 因此文献[5-7]的方法并不能处理问题(3). 本文基于不动点指数理论, 考虑当f有多个零点时, 问题(3)正解的多解性, 并给出解的个数与非线性项f零点个数之间的关系. 本文总假设: (H1)a∈C[0,1]满足0 (H2) 存在两个正的点列ai,bi,ai 1) 若 ‖Tx‖≥‖x‖,x∈∂Kr, 则i(T,Kr,K)=0; 2) 若‖Tx‖≤‖x‖,x∈∂Kr, 则i(T,Kr,K)=1. 引理2假设v∈X使得v(t)≥0,t∈[0,1]. 若v′(t)在[0,1]上非增, 则 v(t)≥min{t,1-t}‖v‖,t∈[0,1]. 特别地, 若v(0)=‖v‖, 则有 v(t)≥‖v‖(1-t),t∈[0,1]. (4) 证明: 因为v是下凸的, 所以结论显然成立. 证毕. 对任意的t∈[0,1],i=1,2,…,n, 定义fi(t,u)如下: (5) 证明: 注意到v满足 引理4假设条件(H1),(H2)成立. 对任意的i∈{1,2,…,n}, 存在ri, 使得[ζri,ri]⊂(ai,bi). 此外, 对任意的v∈∂Ori, 有 证明: 基于ζ的选择, 显然存在ri, 使得[ζri,ri]⊂(ai,bi). 注意到对任意的v∈P, 有v(t)≥v(0)(1-t),t∈[0,1]. 特别地, 由引理1有ζv(0)≤v(t)≤v(0),t∈[0,1-ζ]. 令v∈∂Ori, 则fi(t,v(t))≥ωri,t∈[0,1-ζ]. 又由s1∈(0,1],s2∈[0,∞), φ-1(s1s2)≥s1φ-1(s2)可知, 证毕. 定理1假设条件(H1),(H2)成立, 则存在λ0, 使得对任意的λ≥λ0, 问题(3)存在n个正解u1,u2,…,un, 满足ai<‖ui‖≤bi,i=1,2,…,n. 证明: 定义 注1若存在an>an-1>…>a1>a0>0, 使得f(ai)=0(i=1,2,…,n), 且f(s)>0,ai-1 例1考虑如下边值问题: (6)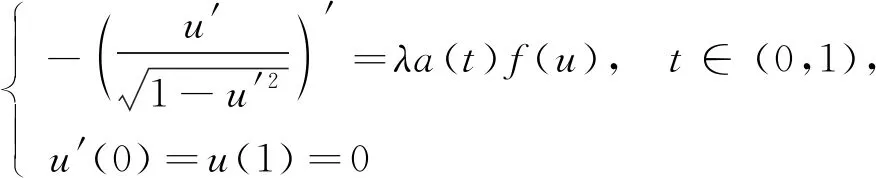

1 预备知识





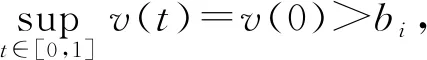
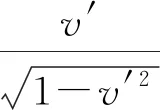
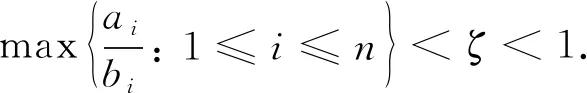

2 主要结果