张量变分不等式解的存在性

牟文杰, 范江华

(广西师范大学 数学与统计学院, 广西 桂林 541006)

0 引 言

考虑如下张量变分不等式问题TVIP(A,q,K): 求向量x*∈K, 使得

〈A(x*)m-1+q,y-x*〉≥0, ∀y∈K,

其中A为m阶n维实张量,q∈n,K是n中的非空闭凸子集. 将TVIP(A,q,K)的解集记为STVIP(A,q,K). 当时, TVIP(A,q,K)转化为张量互补问题TCP(A,q).

张量互补问题[1]是一类非线性互补问题, 简记为TCP(A,q): 求向量x*∈n, 使得

x*≥0,A(x*)m-1+q≥0, (x*)T(A(x*)m-1+q)=0.

目前, 关于TCP(A,q)解集基本性质和迭代算法的研究已取得了许多结果: 对于对称正定张量和共正张量等结构张量, Che等[2]给出了对应张量互补问题解的存在性定理; Song等[3]讨论了半正张量的性质, 并研究了对应张量互补问题解的唯一性; Wang等[4]讨论了ER张量的性质, 并研究了对应张量互补问题解集的非空紧性; Yu等[5]研究了张量互补问题解的稳定性; Luo等[6]讨论了Z张量的一些性质, 并研究了Z张量对应互补问题的稀疏解; Liu等[7]研究了一些特殊结构张量互补问题的全局唯一性和可解性, 并在此基础上给出了相应的非光滑牛顿法.

张量变分不等式在经济均衡和博弈论中应用广泛, 如Nash均衡问题在一定条件下可转化为张量变分不等式问题. 解集的基本性质及迭代算法是张量变分不等式问题研究的重点, 解的存在性研究是张量变分不等式问题理论研究的最基本问题. Song等[1]将一类结构矩阵推广到高阶张量, 提出了一类特殊的张量变分不等式问题; Wang等[8]利用例外族方法, 在0∈K及A在K上正定的条件下, 研究了张量变分不等式问题解集的非空紧性, 在0∈K及A在K上严格正定的条件下, 研究了张量变分不等式问题解的唯一性, 并证明了一类多人非合作对策可以重新表示为一类张量变分不等式问题； Barbagallo等[9]研究了张量变分不等式问题解的不适应性和稳定性, 并将理论结果应用于检验一般的寡头市场均衡问题.

本文研究张量变分不等式问题解的存在性, 首先给出张量变分不等式问题解集为空集的一个必要条件; 其次, 当张量在集合的退化锥上正定时, 证明张量变分不等式问题解集为非空紧致集, 给出张量变分不等式问题解集为非空紧致集的一些强制性条件及张量变分不等式问题解集为非空紧致集的必要条件. 若0∈K, 则K∞⊂K, 从而由A在K上正定可推出A在K∞上正定, 故本文结果的条件比文献[8]中定理4.2的条件弱, 从而推广了文献[8]的主要结果.

1 基本符号和概念

设K是n中的非空子集, 任取令其中表示以为中心、r为半径的开球.表示Kr的内部, 记

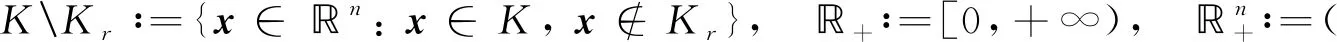
用K∞表示K上的退化锥, 定义为

(1)

若K为闭凸集, 给定x0∈K, 则K∞可定义为

(2)

此时,K∞与x0∈K的选取无关. 由文献[10]中命题2.1.5可知, 当K为闭凸集时, 式(1)与式(2)等价. 对任意给定的正整数n, 用[n]表示集合{1,2,…,n}. 对任意给定的正整数m,r1,r2,…,rm, 一个m阶r1×r2×…×rm维实张量A∈r1×r2×…×rm可表示为(ai1i2…im), 其中ai1i2…im∈对任意ij∈[rj]和j∈[m]皆成立. 特别地, 若对任意j∈[m], 有rj=n, 则称A为m阶n维实张量, 用 Tm,n表示m阶n维实张量的集合. 元素ai1i2…im均为0的张量称为零张量, 记为O.

定义1设A∈Tm,n,v∈n, 则张量A和向量v的k-模式(向量)积记为其分量表示为

其中ij∈[n],j∈[m]k.

定义2设A=(ai1i2…im)∈Tm,n,x∈n, 则Axm-1是n中的向量, 其第i个分量表示为

Axm是m次齐次多项式, 定义为

定义3设A∈Tm,n, 若对任意x∈n{0}, 有Axm>0, 则称A在n上正定.

定义4设K是n中的非空子集,A∈Tm,n, 若对任意x∈K{0}, 有Axm>0, 则称A在K上正定.

下面举例说明A∈Tm,n在K上正定, 在n上不一定正定.

例1设

A∈T3,2, 其中a111=a211=a122=a222=1,a121=a112=a221=a212=-1, 则0∈K. 对任一u∈K{0}, 有

(3)

(4)

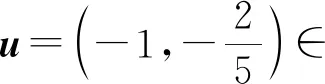
(5)

故A不在n上正定.

定义5设A=(ai1i2…im)∈Tm,n, 若任意置换元素ai1i2…im的下标i1,i2,…,im, 其值保持不变, 则称A为对称张量.

2 解集的非空紧致性

下面考虑张量变分不等式问题解的存在性, 首先给出张量变分不等式问题解集为空集的一个必要条件, 然后给出张量变分不等式问题解集为非空紧致集的几个充分条件.

设K是n中的非空闭凸子集,A∈Tm,n,q∈n. 下面考虑TVIP(A,q,K)在Kr上的限制, 记为TVIP(A,q,Kr): 求向量xr∈Kr, 使得

〈A(xr)m-1+q,y-xr〉≥0, ∀y∈Kr.

将TVIP(A,q,Kr)的解集记为STVIP(A,q,Kr).

引理1设K是n中的非空闭凸子集,A∈Tm,n,q∈n. 对任意给定的若STVIP(A,q,K)=Ø, 则存在序列{xr}r>r0满足下列条件:

2)xr∈STVIP(A,q,Kr).

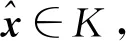
〈A(xr)m-1+q,(1-tr)y+trxr-xr〉≥0,

消去(1-tr), 得

〈A(xr)m-1+q,y-xr〉≥0,

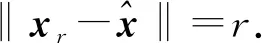
引理1给出了张量变分不等式问题解集为空集的一个必要条件.

引理2设K是n中的非空闭凸子集且0∈K, 若A∈Tm,n在K上正定, 则A在K∞上正定.

证明: 由式(2)可知, 若0∈K, 则K∞⊂K, 结论显然成立.

注1若K为有界集, 则由式(2)可知,K∞={0}, 故任一张量均在K∞上正定.

下面举例说明引理2的逆命题不成立.

例2设

A∈T3,2, 其中a111=a211=a122=a222=1,a121=a112=a221=a212=-1, 则0∈K,

定理1设K为n中的非空闭凸子集,A∈Tm,n,q∈n, 若

Aum>0, ∀u∈K∞{0},

则STVIP(A,q,K)为非空紧致集.

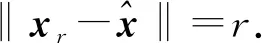
〈A(xr)m-1+q,y-xr〉≥0, ∀r≥r0,

(6)

将式(6)两边同时除以‖xr‖m, 得

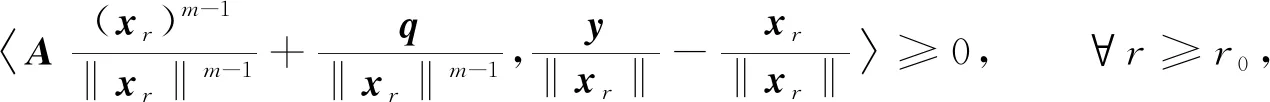
(7)

〈Aum-1,-u〉≥0 ⟹Aum≤0,

与定理1条件矛盾. 因此, STVIP(A,q,K)≠Ø.

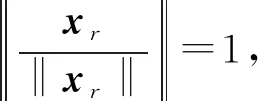
〈A(xr)m-1+q,y-xr〉≥0, ∀y∈K,

(8)

仿照上述步骤可推出矛盾. 故STVIP(A,q,K)为有界集.

最后证明STVIP(A,q,K)为闭集. 设xr∈STVIP(A,q,K),xr→x*, 则有式(8). 令r→+∞, 得

〈A(x*)m-1+q,y-x*〉≥0, ∀y∈K,

即x*∈STVIP(A,q,K). 因此, STVIP(A,q,K)为闭集.

综上可知, STVIP(A,q,K)为非空紧致集. 证毕.

定理1给出了张量变分不等式问题解集为非空紧致集的一个充分条件.

注2当0∈K,A∈Tm,n在K上正定时, 文献[8]中定理4.2利用例外族方法证明了STVIP(A,q,K)为非空紧致集. 当0∈K时, 由引理2可知, 若A在K上正定, 则A必在K∞上正定, 故定理1的条件比文献[8]中定理4.2的条件弱, 从而推广了文献[8]的结果.

例3设

A∈T3,2, 其中a111=a211=a122=a222=1,a121=a112=a221=a212=-1,q=0, 则

对任一u∈K∞{0}, 有式(3),(4), 故A在K∞上正定, 从而满足定理1的条件. 其相应张量变分不等式问题的解集

为非空紧致集. 例2表明,A不在K上正定, 故该例不满足文献[8]中定理4.2的条件.

定理2设K为n中的非空闭凸子集,A∈Tm,n为对称张量,q∈n. 若STVIP(A,q,K)为非空紧致集, 则

〈q,u〉>0, ∀u∈(K∞∩{v∈n:Av=O}){0}.

证明: 用反证法. 假设存在非零向量u0∈K∞且Au0=O, 使得〈q,u0〉≤0. 因为A为对称张量, 且Au0=O, 故

A(x+tu0)m-1=Axm-1, ∀x∈K, ∀t>0.

又因为

〈A(x+tu0)m-1,u0〉=〈Axm-1,u0〉=〈xm-1,Au0〉=0, ∀x∈K, ∀t>0,

所以

〈A(x+tu0)m-1+q,-tu0〉≥0, ∀x∈K, ∀t>0.

(9)

将不等式(9)左边加上

〈A(x+tu0)m-1+q,y-x〉-〈Axm-1+q,y-x〉,

得

〈A(x+tu0)m-1+q,y-(x+tu0)〉-〈Axm-1+q,y-x〉≥0, ∀x,y∈K, ∀t>0.

令x=x*∈STVIP(A,q,K), 得

〈A(x*+tu0)m-1+q,y-(x*+tu0)〉≥0, ∀y∈K, ∀t>0,

故对任意t>0, 有x*+tu0∈STVIP(A,q,K), 这与STVIP(A,q,K)为紧致集矛盾. 故结论成立. 证毕.

定理2给出了张量变分不等式问题解集为非空紧致集的一个必要条件.

注3集合{v∈n:Av=O} 可视为矩阵核的推广.

例4设对称张量A∈T3,2, 其中a111=-1,a112=a121=a211=2,a122=a212=a221=-4,a222=8,

q=(1,1), 则

因此,

从而

可证该张量变分不等式问题的解集为有界闭集, 且(0,0)∈STVIP(A,(1,1),K), 故STVIP(A,(1,1),K)为非空紧致集. 对任一u∈(K∞∩{v∈n:Av=O}){0}, 有〈q,u〉>0, 故满足定理2的条件.

定理3设K为n中的非空闭凸子集,A∈Tm,n,q∈n, 若:

1) 存在y∈K, 使得F(y)={x∈K: 〈Axm-1+q,x-y〉≤0}为有界集(可能为空集);

2) 存在开球Ω⊂n和y∈Ω∩K, 使得

3) 存在一非空有界集D⊂K, 使得∀x∈KD, ∃y∈D: 〈Axm-1+q,x-y〉>0;

4) 对任一满足‖xr‖→+∞的序列{xr}⊂K, 存在xr0∈{xr}和yr0∈intKr0, 使得〈A(xr0)m-1+q,xr0-yr0〉>0;

5) STVIP(A,q,K)为非空紧致集.

则1)⟺2)⟺3)⟺4)⟹5).

证明: 1)⟹2). 由1)知, 存在y∈K, 使得F(y)为有界集, 故存在开球Ω⊂n, 使得F(y)∪{y}⊂Ω, 从而又由1)知,

(10)

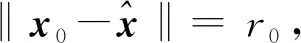
故xr0∈KD. 又由3)知, 存在yr0∈D⊂intKr0, 使得〈A(xr0)m-1+q,xr0-yr0〉>0.

4)⟹3). 对任意r>0,Kr为非空有界集. 假设3)不成立, 则对任意有界集Kr, 存在xr∈KKr, 使得∀y∈Kr, 〈A(xr)m-1+q,xr-y〉≤0, 从而存在序列{xr}⊂K, 且‖xr‖→+∞, 使得

〈A(xr)m-1+q,xr-y〉≤0, ∀y∈intKr.

(11)

由4)知, 存在xr0∈{xr}和yr0∈intKr0使得〈A(xr0)m-1+q,xr0-yr0〉>0, 与式(11)矛盾. 故结论成立.

〈A(xr)m-1+q,xr-y〉≤0, ∀y∈Ω∩K,

(12)

从而xr∈KD. 又由3)知, 存在y0∈D⊂Ω∩K, 使得〈A(xr)m-1+q,xr-y0〉>0, 与式(12)矛盾. 故结论成立.

4)⟹5). 由4)知, 对任一满足‖xr‖→+∞的序列{xr}⊂K, 存在xr0∈{xr}和yr0∈intKr0, 使得

〈A(xr0)m-1+q,yr0-xr0〉<0.

(13)

首先, 用反证法证明STVIP(A,q,K)≠Ø. 假设STVIP(A,q,K)=Ø, 则由引理1知, 存在序列{xr}使得xr∈STVIP(A,q,Kr), 从而∀x∈Kr, 〈A(xr)m-1+q,x-xr〉≥0. 令r=r0,x=yr0, 与式(13)矛盾. 故STVIP(A,q,K)≠Ø.

其次, 用反证法证明STVIP(A,q,K)为有界集. 假设STVIP(A,q,K)为无界集, 则存在序列{xr}, 使得xr∈STVIP(A,q,K), 且‖xr‖→+∞. 于是∀x∈K, 〈A(xr)m-1+q,x-xr〉≥0, 仿上述取法可推出矛盾. 故STVIP(A,q,K)为有界集.

与定理1类似, 可证STVIP(A,q,K)为闭集. 因此, STVIP(A,q,K)为非空紧致集. 证毕.

定理3给出了张量变分不等式问题解集为非空紧致集的一些强制性条件.

定理4设K为n中的非空闭凸集,A∈Tm,n,q∈n. 若对任意实数p>0, 存在使得

则STVIP(A,q,K)为非空紧致集.

(14)

(15)