基于MRF的配电网线损原因识别方法*
2021-05-24拜润卿陈仕彬
拜润卿,何 欣,陈仕彬
(国网甘肃省电力公司 电力科学研究院,兰州 730070)
配电网位于电力系统的末端,其地域分布较广、规模较大,且所包含的电力设备类型较多,连接和运行方式呈现多样化的特点[1-2].随着分布式电源大规模接入电网,配电网逐渐演化为多向交互系统,由此导致的潮流随机性逐渐增加,预测线路损耗变化规律的难度也显著提升,进一步加大了分析线路损耗的困难[3].
此外,在配电网对电能进行分配的过程中,不可避免地会出现一定的线路损耗[4-5].目前,配电网线损分析的研究重点主要是规划分析和理论计算.汲国强等[6]提出了一种以降损和平衡负载为目标的快速区域网络重构算法.将降损问题转化为多目标优化问题,以平衡支路负荷为目的,求出整个区域的线损.李亚等[7]提出了一种基于改进K均值聚类算法和Levenberg-Marquardt算法的BP神经网络模型,能够对低压配电站的线损率进行快速计算,实现配电网理论线损率的快速计算,并由此可以确定配电网的高损耗线路.然而,由于配电网结构复杂、负荷多样化,电网运行方式频繁变化,设备质量水平参差不齐,外部环境、气象和地貌等因素影响较多,难以准确识别配电网线路损耗的原因,由此本文提出一种识别配电网线路高损耗原因的方法.利用与线损变化相关的数据建立了配电网线损识别模型,通过使用与线损位置相关的各种先验条件模糊性和不确定性实现线损的识别.
1 MRF法原理
MRF法是一种基于Markov模型和贝叶斯理论的概率统计方法,其原理是利用无向图来组织某一随机分布的Markov过程,在此基础上采用由无向图设计的图谱模型来表征联合分布.MRF实质是由多个Markov链组成的无向图,其状态跃迁可以通过向量序列进行观察,每个观测向量由不同的概率密度分布函数进行表示,并由一系列具有相应概率密度分布的状态序列生成[8-10].
本文构建了一个隐Markov模型五元组,MRF{N,M,π,A,B},其中:N为隐藏状态数;M为可观察状态数;π为初始状态概率;A={aij}为隐藏状态的迁移概率矩阵;B={bij}为隐藏状态与输出状态的可观测概率关系矩阵.隐藏关系随机场结构如图1所示,其中X代表随机场中的状态节点,Y代表可观测到的状态节点输出.图1中MRF的状态节点及其输出之间基于可观测概率的相互关系可以表示为矩阵形式.
构建MRF随机场步骤如下:1)通过对线损原因的梳理,归纳总结配电网线损特征和线损解决措施,初始化显示线损状态序列集合、形成隐藏的线损原因序列集合,并根据这两个集合初始化隐Markov五元组;2)初始化隐Markov五元组中的其他变量,通过设置两个变量的先验概率和后验概率,不断更新隐Markov参数以找到输出状态在隐藏状态下的节点迁移概率和可观测概率,递归直到建立最优隐Markov模型;3)基于隐Markov模型,输入给定线损原因的状态序列,提取所有状态序列,确定每个状态的最大概率和路径,然后依次得出可能的线损原因.

图1 随机场结构示意图Fig.1 Schematic diagram of random field structure
使用MRF法时,可以在已知隐Markov模型的条件下获得输出序列,或是在已知输出状态序列找到最优隐藏状态序列,并利用输出和隐藏状态序列集构造隐Markov模型.
2 配电网线路损耗分析
当前配电网产生线路损耗的原因较为复杂,从线路损耗的趋势和分布来看,线路拓扑结构、电力设备水平和负荷变化情况是影响线路损耗的主要因素[11].而由于配电网具有线路变化频繁、设备类型多样和负荷动态变化的特点,使得配电网的线路损耗也随之产生复杂的变化.图2给出了兰州市配电网不同位置馈线13天内线路损耗的变化情况,并将市内不同位置馈线13天的每日线损率进行对比.线路基准电压为10 kV,输电线路型号为JL-GlA铝钢绞线,线路截面积为115.67 mm2,线路直流电阻率为0.385 4 Ω/km,线路电抗率为0.452 7 Ω/km,线路长度为20 km.6条馈线分别对应兰州市城关区、七里河区、西固区、安宁区、红古区和高新区.
由图2的对比结果可以看出,线损率的变化与线路所在位置有关.但线路所在位置有诸多因素影响线路损耗,难以直接确定线损原因.此外,由于测量仪表误差和分布式电源并网波动,使得部分线路线损率为负.而MRF法由于可以在已知输出状态序列条件下找出最优隐藏状态序列,确定其相关关系,因此,可以引入MRF法对线路损耗原因进行识别.
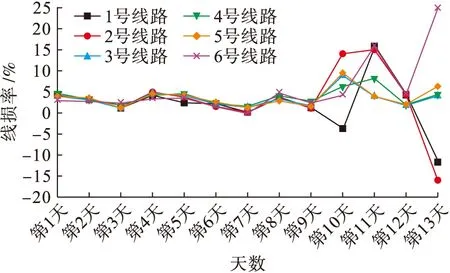
图2 配电网馈线线路损耗对比图Fig.2 Comparison of feeder line loss in distribution network
3 识别算法
由于配电网中线路损耗具有不确定性,因此在识别配电网高线损原因的过程中,可通过确定配电网运行过程中造成线损波动风险的各种因素对线路状态进行分析,研究各种因素改变对线损的影响,将不确定性有限状态机模型与MRF无向图表示方法相结合,形成一种基于MRF的配电网线损原因识别方法.在不确定性有限状态机模型实现过程中,新的状态节点是在添加迁移映射过程中生成的.在这一过程中不确定性有限状态机并未介入,而是从开始状态起步,不断迭代找出所有的状态节点.主要步骤是:采集影响线损分布的各种高损耗因素的有关数据,然后对线损及其形成原因的样本进行训练,形成损耗原因识别模型,最后,将正常线损值、线损率、线损负荷和配电网结构代入识别模型,得到线损的可能原因和概率,其流程图如图3所示.
MRF主要用于分析无向图状态,可以利用隐Markov模型构造一个训练过程.根据线路损耗值、线路损耗率、电网拓扑结构、售电量变化和配电网历年线损数据等影响因素推断出线路损耗原因[11],该模型可基于前向与后向算法得到MRF的局部最优解.
定义正辅助变量γ(Xt,Xt+1)为在时间t和时间t+1产生线路损耗的概率,即
γ(Xt,Xt+1)=P[P(Xt=xi),P(Xt+1=xi)]
式中,Xt和Xt+1分别为t时刻和t+1时刻的随机场,则有
(1)
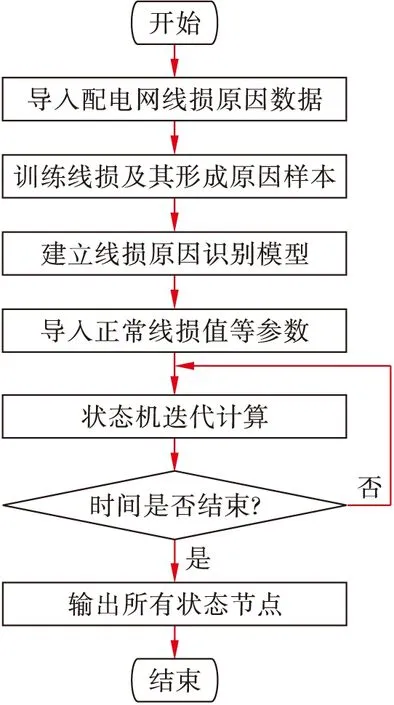
图3 基于MRF的配电网线损原因识别方法流程图Fig.3 Flow chart of cause identification method for line loss of distribution network based on MRF
定义逆辅助变量为φ(Xt),给定t时刻的可观测序列、隐Markov模型五元组和概率P(Xt=xi),可以得到
φ(Xt)=P[P(Xt=xi)]
(2)
即为
(3)
将式(1)代入式(2)得
(4)
4 实例验证
为了验证本文提出的基于MRF配电网线损原因识别方法的有效性,文中选取某地区200条馈线全年的线路损耗数(表1给出了部分馈线线路损耗样本数据),分别采用支持向量机(SVM)[12]、人工神经网络(ANNs)、随机场(RF)、贝叶斯分类算法(BCA)和MRF法对线损原因进行识别.在对比这5种算法用于配电网线损原因识别的性能时,首先需要对数据库中的历史数据进行遍历,从而构建训练模型.这一训练过程所需时间称为训练时间,该训练时间可用于评估算法的性能.训练模型构造完成后,模型开始自动运算,对配电网馈线线损原因进行识别,确定配电网的馈线损耗原因,并与数据库中的识别结果进行对比,得到的对比结果如图4所示.
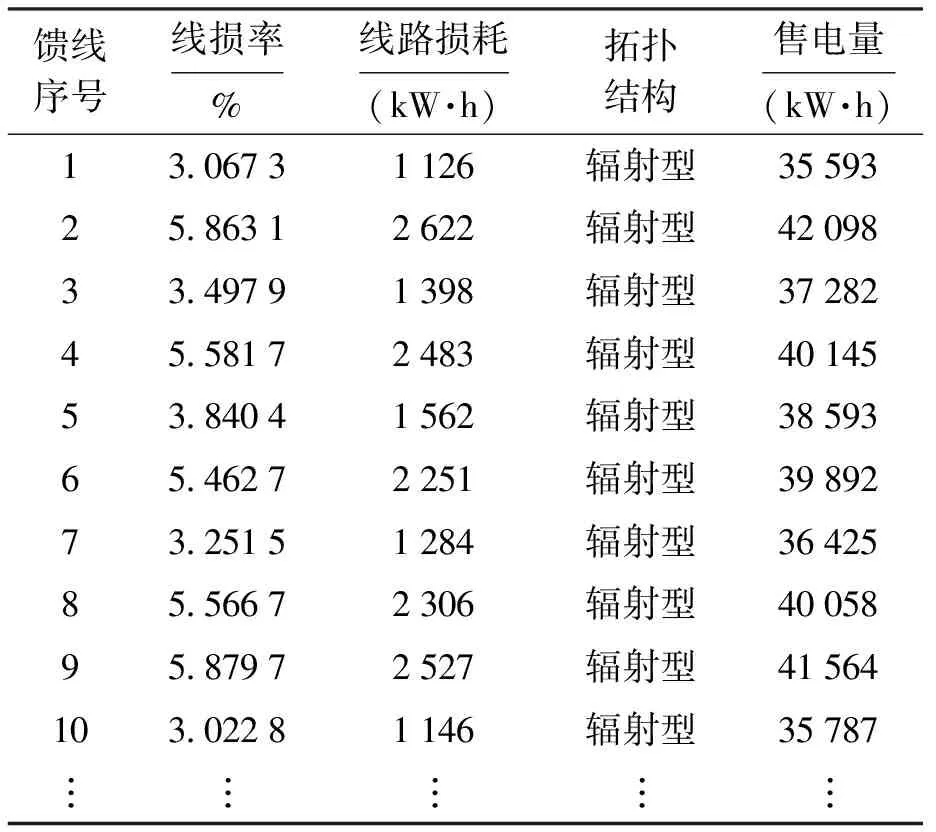
表1 部分馈线线路损耗样本数据Tab.1 Partial feeder line loss sample data

图4 配电网线损原因识别结果Fig.4 Cause identification results of line loss of distribution network
从图4可以看出,针对配电网线损原因进行识别所采用的5种算法中,本文所提出的MRF算法的训练时间为0.3 s,仅大于SVM算法所用训练时间,同时运算时间与SVM算法一致,均为最短时间.同时,对配电网线损原因识别的正确率达到82.6%,能够较好地满足工程实际的需要.对比5种算法识别结果可以看出,MRF算法在正确率、训练时间和运算时间等评价指标中均有着较好表现.MRF在各算法中具有较好的实用性,性能更为优秀,从而可有效实现配电网线损原因识别.由于MRF法能够实现自推理过程,可以根据历史数据进行快速的概率推算,在概率计算的基础上对配电网线损原因进行识别,不会丢失信息,而其他几种算法主要是将一切线路损耗状态和原因转化为数值计算,由此导致参量过多,运算时间增加,易丢失状态信息,导致正确率下降.
5 结 论
本文提出了一种基于MRF的配电网线损原因识别方法.该方法将线损率、线路损耗、拓扑结构和售电量等变量导入MRF模型,进而推导出配电网线路损耗的原因.基于MRF的配电网线损原因识别方法能够较为准确地识别出配电网线路损耗,且由于MRF的运算过程属于多向随机过程,能够避免在运算时产生分类边缘的混叠问题,从而有效提升样本训练时间与运算时间.该方法具有快速、精确和简便等特点,能够较好地满足工程应用,有助于配电网的线损预测研究.
