利用非线性模型提高加长型热脉冲双探针土壤热参数测定精度*

任姮烨，司炳成，2，3†，李 敏，胡 优

（1. 西北农林科技大学旱区农业水土工程教育部重点实验室，陕西杨凌 712100；2. 萨斯喀彻温大学土壤科学系，萨斯卡通 S7N5A8；3. 鲁东大学资源与环境工程学院，山东烟台 264025）

热脉冲双探针对土壤破坏小，成本低廉，可连续获得原位数据，被广泛应用于土壤热参数、含水率[1-5]、土壤容重[6]等测定中。常规双探针长度仅为2.8 cm，测定土壤体积有限，不能满足水文、环境和农业监测的现实需求，增加探针长度可增加双探针测量体积，从而增大测量结果代表性，但同时增加探针长度会导致倾斜而产生误差[2，7-8]。

为减少探针倾斜的影响，Kamai 等[9]和 Satio等[10]通过将探针直径增至4 mm 以上使探针更为坚固，而Mori 等[11]将探针长度缩短至1.3 cm。但以上两种方法会偏离将有限性探针看作无限线性热源的假设。Liu 和Wen 等[12-14]通过改进感应探针（内含热感应元件）的设计先后提出了原位间距校正方法的线性模型和非线性模型，并分别采用一阶和二阶函数对探针间距进行校正。测试结果表明利用线性模型可有效减小探针共面倾斜下的土壤容积热容的误差，对于非共面、探针弯曲的倾斜无法准确校正[13，15]。其优点是感应探针仅包含2 个热敏电阻，制作简单，要求的数据采集仪接口数量少，可减小仪器成本，因此，优先选择线性模型校正探针间距变化。而非线性模型在此基础上还可校正非共面倾斜下和探针弯曲引起的测量误差，但要求感应探针中至少安装3 个热敏电阻，增加了需要的数据采集仪接口数量和仪器成本。线性模型和非线性模型为增加探针长度从而增加测定体积提供了理论基础，但探针长度越长就越容易倾斜，导致的误差越大，当使用加长型探针时，优先考虑的线性模型是否仍然适用值得进一步探讨。

为了解决上述问题，本研究将双探针加长至10 cm，对于探针倾斜所产生的误差利用Liu 等[13-14]提出的理论进行修正，通过对比不同模型校正后的土壤热参数值与理论值，评价了线性模型和非线性模型对于长探针间距误差校正的适用性。本研究将加长型探针长度定为10 cm 的原因：（1）测定体积较大的热脉冲单探针长度为10 cm[16]；（2）热脉冲-时域反射探针长度超过10 cm 时，会提高测定含水率的精度[17]。（3）分布式光纤测温的最小分辨率也在10 cm 左右[18]。随着热脉冲-光缆和热脉冲-时域反射技术的发展[13，19-22]，本研究选取的10 cm 探针长度是可以更好地体现上述测试技术的优势，具有较广的应用前景。

1 材料与方法

1.1 热脉冲双探针原理

热脉冲双探针由一组间距为r 的加热探针和感应探针构成（图1）。根据热传导理论，在一个无限大的均匀等温介质中，无限线性热源发出t0时长的热脉冲，距热源径向距离r 处温度随时间的变化可表达为[1]：

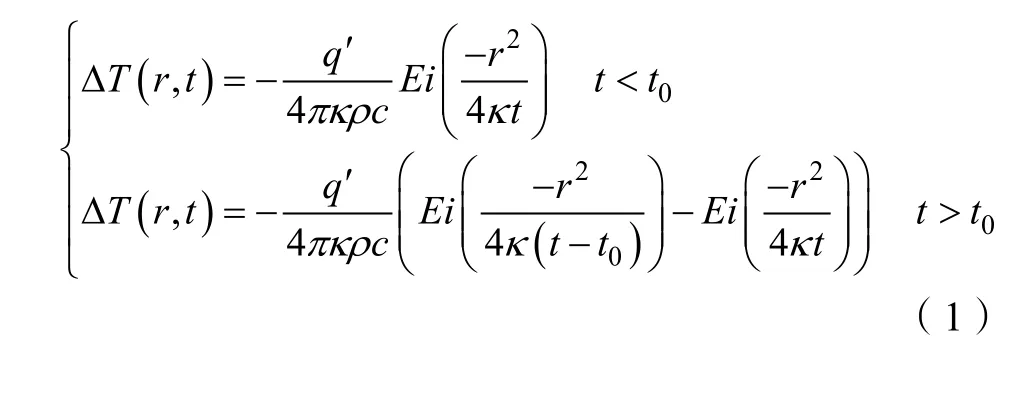
式（1）中，ΔT 为温度变化值（℃），t 为时间（s），q′为单位长度加热丝在单位时间内释放的热量（W·m–1），κ 为土壤热扩散系数（m2·s–1），ρc 为土壤容积热容（MJ·m–3·K–1），Ei（–x）为指数积分。对式（1）求t 的偏微分并使结果等于零，得到κ 和ρc 为：

式（2）和式（3）中，tm为最大升温值对应的时间（s）。

根据de Vries 模型[4]，土壤容积热容表达式为：

式（4）中，ρwcw为水的容积热容量（MJ·m–3·℃–1）；θw为土壤体积含水率（m3·m–3）；cs为土壤固体的比热（J·kg–1·℃–1），ρb为土壤容重（kg·m–3）。由式（4）可以反推土壤含水率θw的计算公式：

纯水在20℃时容积热容量为4.18 MJ·m–3·K–1，土壤固体比热值在干土中使用长探针测定获得，其值为844.35 J·Kg–1·K–1。

1.2 原位间距校正方法

双探针测定的容积热容对两支探针的间距很敏感。将热探针插入土壤时，易造成倾斜，从而引起探针间距的改变。考虑倾斜的原位间距校正方法（线性模型和非线性模型）可减小探针间距改变带来的测量误差。当探针发生共面倾斜时，可在感应探针中放置2 个热敏电阻并用线性模型校正探针间距；当探针发生非共面倾斜时，则需要在感应探针内放置至少3 个热敏电阻并使用非线性模型校正探针间距[12，23]。其中共面倾斜指倾斜后的加热和感应探针共平面，非共面倾斜则指倾斜后的两支探针不共平面。Wen 等[24]进一步将线性模型和非线性模型简化为一个模型并给出了求解方法：

假设感应探针分别距底座距离l1，l2，l3处放置3 个热敏电阻（图1，以下简称热阻1，热阻2，热阻3；其中，线性模型仅有热阻1 和2），定义tmi为热敏电阻i 的温度响应曲线达到最大值ΔTm时对应的时间（线性模型：i=1，2；非线性模型：i=1，2，3），并定义ηi为：

对于均质土壤，各处热敏电阻热扩散率相同，根据式（2）可得：

式中，线性模型只用到p 值，非线性模型则会用到p 和p2值。定义探针未发生倾斜时各热敏电阻与加热探针的间距为初始间距ri0，探针间距偏移量为Δri，则探针发生倾斜后的新间距（校正间距）ri为：

外倾Δri为正值，内倾反之；a，b 值为回归系数，对于线性模型，b=0。对于共面倾斜，可利用线性模型校正（b=0），非共面倾斜则需利用非线性模型校正（b≠0），a，b 值的求解过程参考Wen 等[24]。求得的a，b 值代入式（8）则可获得倾斜后的校正间距（线性模型：r1，r2；非线性模型：r1，r2，r3）。

图1 加长型双探针示意图Fig. 1 Schematic of the apparatus with extended dual probes

1.3 试验装置

加长型热脉冲双探针的长度为10 cm，外径为1.3 mm，内径为0.9 mm，材料为304 不锈钢。探针设计应符合一定规则，Blackwell 等[25]指出探针长与半径比值大于25，Liu 等[26]建议热敏电阻距离探针顶部与底部的距离应大于1 cm，Kluitenberg 等[27]提出探针建议不宜过大（＜8 mm），否则需要较大的功率加热，易造成水分蒸发。本文采用探针，长度半径比为77，间距为6 mm，符合上述要求。加热探针内置镍铬绝缘电阻丝（阻值为86 Ω·m–1）。感应探针中有3 个热敏电阻（10K3MCD1，Betatherm Corp.，Shrewbury MA），为满足线性热源模型，分别放置在距底座距离l1= 70 mm，l2= 50 mm，l3=30 mm的位置。并在两个探针内填充高导热性能的环氧树脂（Omega engineering，Stamford，CT）。两根探针通过环氧树脂胶固定在圆柱形PVC 底座（壁厚5 mm，直径30 mm，高35 mm），组成热脉冲探头（图1）。热脉冲探头固定在PVC 土柱底部（高13.4 cm，外径5.5 cm，壁厚0.5 cm）。室内恒温条件下（20℃），利用浓度为5 g·L–1的琼脂溶液标定双探针初始间距（图1），其中琼脂溶液的容积热容与去离子水相同，为4.18 MJ·m–3·K–1。双探针与数据采集仪（Model CR1000，Campbell Scientific，Logan，UT）采用四线半桥的方法连接。为保持探针加热电流稳定，数据采集仪和探针电阻丝分别采用独立的12V 恒压蓄电池供电。热脉冲时长 t0= 15 s，加热功率q′≈ 45W·m–1，采样频率为1 Hz。

1.4 试验过程

研究表明双探针测定土壤水热参数和原位间距校正方法的规律不受土壤质地的影响[1，12，14，24，28]，本研究选择砂土作为供试土样。土样取自陕西杨凌渭河沿岸，其黏粒（＜0.002 mm）、粉粒（0.002～0.05 mm）和砂粒（＞0.05 mm）的质量分数分别为0.03、0.09和98.8 kg·kg–1。供试土壤进行过筛（1 mm）和烘干处理后，称取所需质量的烘干砂土，加入一定质量的去离子水，配成质量含水率梯度为0、5%、10%、15%、20%的土壤，按目标容重1.60 g·cm–3装于PVC土柱并于恒温条件下使土壤水分充分平衡。测定过程控制室内环境温差小于±1℃。

为满足3 个热敏电阻处热扩散率相等的前提假设，将热脉冲双探针和土柱平行于水平面横向布置，以减小重力作用带来土壤水分分布不均匀的影响。如图2 在土样中人为模拟探针在田间土壤里可能出现的四种倾斜方式（图2），共面外倾（OD1）、非共面外倾（OD2）、共面内倾（ID1）和非共面内倾（ID2）。人为倾斜以聚氨酯橡胶材料控制，因其用量极小，其对测量结果的影响可忽略不计。倾斜后3 个热敏电阻处探针校正间距见表1。以上土柱试验对每种倾斜方式（OD1、OD2、ID1 和ID2）设4 个重复（独立填装4 次），每个重复加热3 次。

图2 不同倾斜方式示意图Fig. 2 Schematic of different ways of deflection

表1 利用非线性模型计算得到不同倾斜方式倾斜后的新间距Table1 New probe spacings of different types of deflection corrected by the non-linear model

1.5 数据处理和误差分析

为了分析线性模型和非线性模型对于加长型探针的适用性，利用线性模型和非线性模型分别校正上述干土中四种倾斜方式（OD1、OD2、ID1、ID2）下的探针间距，将以新间距获得的土壤比热作为实测值并与理论值进行相对误差分析，理论值为探针未倾斜时测定的土壤比热。相对误差（ER）可定义为：

式（9）中，ER 代表相对误差，x实测值代表实测值，x理论值代表理论值。

为验证长探针测定土壤热参数的可行性，利用适用于长探针的校正模型校正不同含水率下的土壤在探针外倾和内倾时的探针间距，以校正的新间距拟合土壤容积热容和热扩散率，二者的乘积即为土壤热导率。感应探针共有三个热敏电阻，每个热敏电阻位置均可得到新的校正间距并拟合得到相应的容积热容和热导率，取这三个新间距拟合的容积热容和热导率的平均值作为土壤容积热容和热导率的实测值。土壤容积热容的理论值则可根据式（4）计算，其中土壤容重为填装容重，含水率由烘干法获得，土壤的固体比热为利用长探针测定的探针未倾斜时的土壤比热值。土壤热导率的测定不受探针间距和长度的影响[29-31]，以初始间距拟合计算的热导率作为理论值。为验证长探针测定含水率的可行性，将土壤含水率实测值与烘干法测定的含水率进行比较，实测土壤含水率根据式（5）计算，其中土壤容积热容为新间距拟合得到的容积热容。本研究通过Matlab 内置的solve 函数和lsqcurvefit 函数计算校正后的探针间距和非线性拟合热参数。

2 结果与讨论

2.1 长针原位间距校正模型的选择

图3 温度响应曲线和拟合曲线Fig. 3 Measured curves and fitting curves of temperature

表2 校正探针外倾（OD2）的间距和拟合的热参数Table2 Corrected probe spacings and fitted thermal parameters for probes deflected outwardly（OD2）

温度变化最大值ΔTm值依次增大。这是由于热量在相同的土壤介质中的传播速度相同，探针间距越小，温度上升就越快。探针间距分别使用线性模型和非线性模型校正后的新间距（表2），结合相应的实测温度响应曲线，以最小二乘法拟合，获得相应的拟合曲线并得到容积热容和热扩散率。使用非线性模型计算的新间距（表2）结合热阻1、热阻2 和热阻3 的实测温度响应曲线拟合热传导方程（公式（1））得到了图3 中的拟合曲线，残差平方和结果见表2。线性模型计算的新间距结合实测温度响应曲线进行拟合也可获得相似的拟合曲线，残差平方和结果见表2。对于相同的实测温度响应曲线，不同的新间距拟合热传导方程（公式（1））得到的拟合曲线相似，校正得到的新间距不同，则所得的容积热容和热扩散率不同（表2）。以上以OD2 为例，OD1、ID1 和ID2 的相应结果也很类似。

由表3 可知，对于共面倾斜（OD1、ID1），未校正时干土比热相对误差为33.94%，经非线性和线性模型校正探针间距后，干土比热相对误差分别为–8.30%和43.90%。对于非共面倾斜（OD2、ID2），未校正时干土比热相对误差为32.65%，经非线性模型和线性模型校正探针间距后，干土比热相对误差分别为6.07%和31.94%。上述结果表明，无论是共面倾斜还是非共面倾斜，经非线性模型校正间距后，比热测定准确度大幅提高，而线性模型未能明显减小加长型探针的间距误差，说明加长型探针的间距校正宜用非线性模型，而不宜用线性模型。这是由于线性模型只能校正未发生弯曲的探针在共面倾斜情况下的间距误差。而对于加长型探针，加热探针和感应探针在被人为控制发生共面倾斜的过程中，不可避免地发生轻微弯曲，从而影响线性模型的校正效果，而非线性模型则可有效地考虑轻度弯曲，有效减小探针弯曲时比热测定误差。综上，非线性模型校正可明显减少加长型双探针弯曲造成的间距误差。

表3 线性模型校正、非线性模型校正间距误差和未校正间距的比热（cs）相对误差Table3 Relative errors in heat capacity with spacing error corrected with the linear model，non-linear model

2.2 非线性模型校正后土壤热参数与理论值比较

由2.1 可知，相比线性模型，非线性模型更适于长探针的间距校正，故下文只考虑使用非线性模型校正长探针测定土壤热参数和含水率的间距误差。探针倾斜对于土壤热导率的测试结果影响很小[30]，图4 是长探针实测的经非线性模型校正的土壤热导率和理论值的比较，可以看出，无论探针处于外倾还是内倾，长探针测定的土壤热导率与理论值基本位于1∶1 线上（R2为0.996），说明利用非线性模型校正，可以获得准确的土壤热导率。

由图5 可以看出，探针间距变化给土壤容积热容测定带来较大误差（未校正时外倾和内倾的RMSE 分别为0.152 MJ·m–3·K–1和0.766 MJ· m–3· K–1）。非线性模型修正后的土壤容积热容准确度大幅提高（外倾和内倾的RMSE 分别为0.136 MJ·m–3·K–1和0.173 MJ·m–3·K–1，图中仅列出非线性模型校正后的结果）。未校正间距误差时，探针外倾会高估容积热容，探针内倾结果相反，这与Wen 等[14]对常规短探针的研究结果一致。内倾未校正结果偏离 1∶1 线程度较高，这是由于内倾倾斜程度更大。经过校正后，内倾和外倾校正在高含水率范围（＞0.2 m3·m–3）会高估土壤容积热容（外倾平均相对误差+6.8%，内倾相应值为+8.7%）；低含水率范围（＜0.2 m3·m–3）校正的土壤容积热容与理论值相比较整体表现为低估（外倾平均相对误差为–5.8%，内倾相应值为-6.1%），低含水率范围的校正结果略优于高含水率范围。分析其原因在于：第一，根据非线性模型，校正后的新间距只由温度到达最大值的时间tm决定，而tm值却由间距和土壤含水率共同决定。含水率增加或探针间距减小，均导致tm值减小，但非线性模型中的tm值难以体现间距和含水率的双重变化，当含水率较高时非线性模型校正会低估探针间距，从而造成土壤容积热容的高估，含水率较低时则相反。第二，探针长度越长，初始间距校准的不确定性更大[32]，长探针会引起更大的初始间距测定误差，从而影响容积热容的准确测定。第三，热扩散率相等是精确校正容积热容间距误差的前提。使用长探针时应尽量避免土壤水分重力作用，保证三个热敏电阻处含水率相同，以满足三个热敏电阻热扩散率相等。由于土壤含水率较低时受重力影响较小，故受低含水率范围的校正结果优于高含水率范围。

图5 非线性模型校正间距和未校正间距容积热容计算结果Fig. 5 Volumetric heat capacities acquired with probe spacing corrected or not with the non-linear model

2.3 非线性模型校正后的土壤含水率

土壤质地和容重一定时双探针测定的土壤含水率取决于土壤容积热容。图6 说明长探针测定的土壤含水率和容积热容的规律基本一致，探针间距变化导致较大土壤含水率测定误差（外倾和内倾的RMSE 分别为0.035 m3·m–3和0.188 m3·m–3），但经非线性模型修正后，土壤含水率的测量精度提高（外倾和内倾的RMSE 分别为0.034 m3·m–3和0.038 m3·m–3，图中仅列出非线性模型校正后的结果）。

2.4 测试结果的不确定性

测试结果的不确定性来自四个方面：第一个方面是，热源本身造成的不确定性有热源尺寸、加热功率、探针倾斜、电阻随温度变化等。第二个方面是土壤的不均匀性、各向异性和导热系数变化的多解性，主要有土壤矿物成分、密度、颗粒大小、孔隙比、孔隙分布特征、有机质含量等。第三个方面是由于确定温度上升曲线到达最大值的时间tm时存在误差，tm值受到信噪比、热敏电阻的测定精度及响应速度的影响。第四个方面，原位间距校正模型基于不同热敏电阻处土壤的热扩散率相等的前提假设，因此土壤水分分布的均匀程度对测定结果也会产生一定的影响。

图6 非线性模型校正间距和未校正间距土壤含水率计算结果Fig. 6 Soil water contents acquired with probe spacing corrected or not with the non-linear model

3 结 论

本研究基于原位间距校正方法，将热脉冲双探针的长度加长至10 cm，人为进行探针倾斜，并对砂土进行长针水热参数的测定，以评价线性模型和非线性模型对于长探针的适用性。结果表明，无论是共面倾斜还是非共面倾斜，非线性模型能够明显提高长针测定土壤比热的准确性，相对误差为–8.30%；而线性模型校正效果不明显，相对误差达43.90%，因此，非线性模型适于长探针，而线性模型对于长探针间距校正存在一定局限性。探针间距变化对土壤热导率测定无影响，但给土壤容积热容和含水率测定带来较大误差；使用非线性模型修正后，长探针测定土壤容积热容和含水率的准确度大幅提高，相对误差在10%以内。当前影响非线性模型校正长探针间距误差的主要因素是：非线性模型得到的校正间距由温度响应曲线到达最大值的时间tm决定，而tm值却由间距和土壤含水率共同决定。因此，修正非线性模型中的tm值以体现间距和含水率的双重变化有望进一步提高非线性模型校准探针间距的精度。