基于几何画板软件的热敏电阻温度计参数优化
2022-10-20乐续明原安娟刘立英王丽香常兴阳
乐续明,原安娟,崔 敏,刘立英,王丽香,张 睿,常兴阳
(1.北京工业大学 信息学部,北京 100124;2.北京工业大学 理学部,北京 100124)
动态几何画板(The Geometer’s Sketchpad)是一款相对精确的数学作图软件,由美国Key Curriculum Press公司研制而成,被广泛应用于数学、物理等学科的教学中。几何画板以其所具有的编辑功能、函数与几何作图功能,在数学和物理教学中得到广泛应用,在优化教学过程中起着重要的作用。利用几何画板,可以将抽象的知识进行形象化处理,降低知识难度,提高学生的学习兴趣。利用几何画板特有的“动画功能”,能够十分便利地将一些抽象的物理量变化过程进行动态、分步展示,呈现出连续动态表现效果[1]。
“热敏电阻温度计的设计与标定”实验,是我校理工科学生必修的一个设计性研究性实验[2],该实验具有实用性强、设计内容丰富、创新点多、选材方便等优势,是从基本教学实验向科学实验的过渡,因此很多学校采用该实验作为设计性实验项目[3-7]。
文章利用几何画板的特点,设计热敏电阻温度计的各个参数,并通过动态图像,模拟出电流和温度的线性关系,并计算出热敏电阻承载的功率。
1 热敏电阻温度计的工作原理
图1的电流型非平衡电桥改装热敏电阻温度计的设计方案被广泛采用[8]。其中Rx为负温度系数热敏电阻,其室温25 ℃时的阻值约为5 000 Ω,最大允许功率1 mW,热敏电阻材料常数B=3 950 K。Rg为微安表的内阻(Rg=160Ω),R1、R2和Rs为待设计电阻,E为待设计电源电压。为了使设计简单,同时兼顾电桥的灵敏度,实验中往往选择R1=R2,其大小设定为测温范围内Rx的某一特定阻值即可[2,9]。

图1 电流型非平衡电桥电路原理图
热敏电阻温度计实验的设计重点是要使微安表流过的电流与温度之间尽可能成线性关系,还要兼顾热敏电阻的最大功率、测温范围等。文章侧重于优化微安表电流和温度关系的线性关系,动画显示不同温度下热敏电阻的阻值和热敏电阻上功率的大小。在兼顾测温范围、灵敏度、线性关系等因素的前提下,得到各个元器件参数的最优组合。
2 用几何画板设计非平衡电桥温度计的各参数值
2.1 计算热敏电阻在不同温度下的阻值
文章使用的是负温度系数热敏电阻(NTC),已知B=3 950 K,t=25 ℃,Rt=25 ℃=5 000Ω。热敏电阻的阻值R(x)是温度x的函数,t0为室温,RN=室温值可测出来,可把此条件作为初始值代入(1)式中,即可得到各温度下热敏电阻的大小,图2a是根据(1)式得到的电阻和温度的关系图。
(1)
以t0=25 ℃、Rt=25.0 ℃=5 000Ω为例,当设置出温度x的取值范围(25.0、75.0),并点击“生成x参数的动画”,可动态得到热敏电阻在此温度区间内温度对应阻值的大小,部分阻值截图如图2b、2c、2d所示。
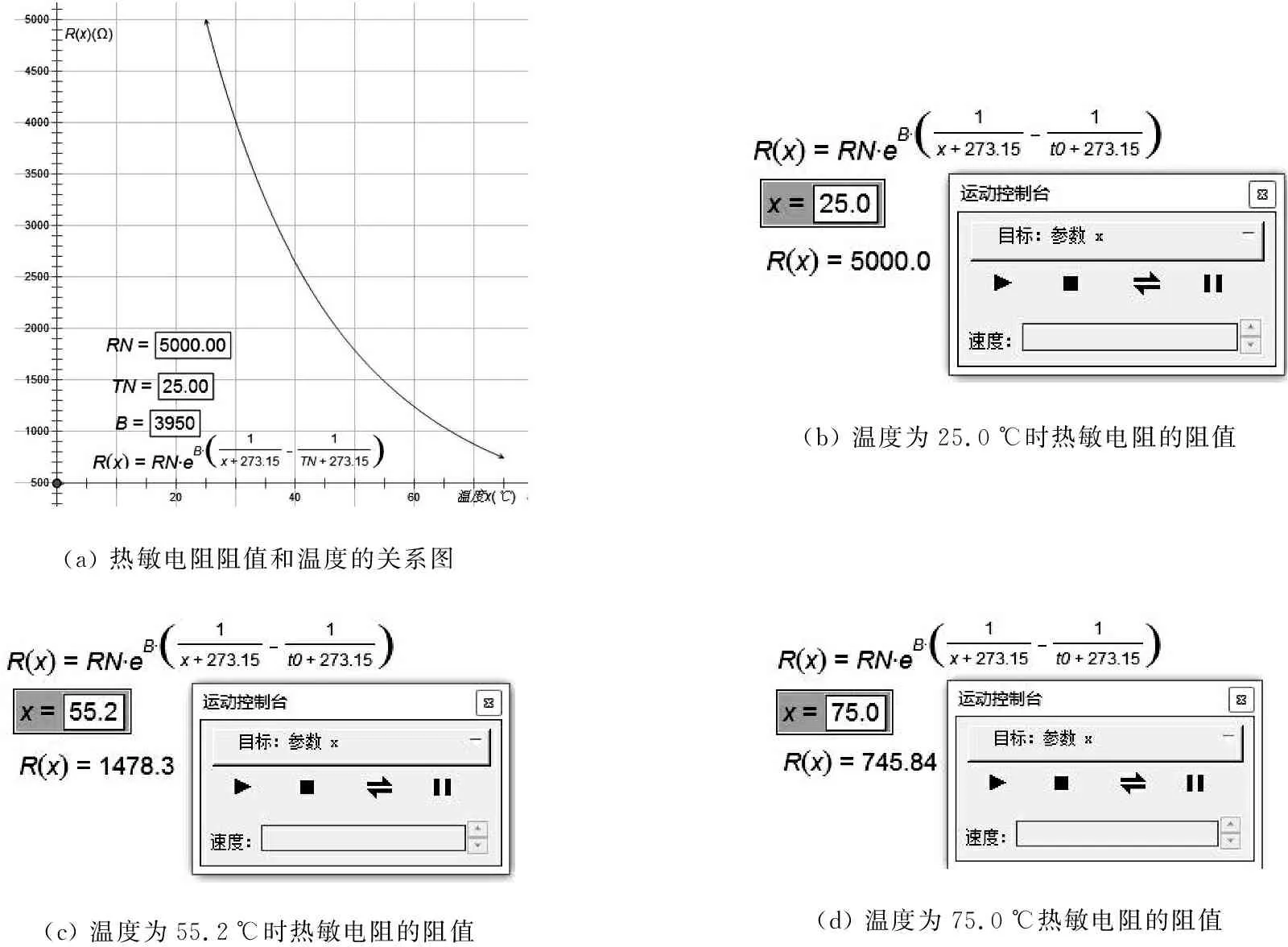
(a) 热敏电阻阻值和温度的关系图(b) 温度为25.0℃时热敏电阻的阻值(c) 温度为55.2℃时热敏电阻的阻值(d) 温度为75.0℃热敏电阻的阻值
2.2 计算电源电压的大小
计算出Rt=75.0 ℃=745.84Ω后,把已知值代入(2)式中,可以得到电源电压E的大小。
(2)
电源电压的大小,一要保证非平衡电桥的灵敏度,二要做到t=75.0 ℃时微安表达到满偏300μA,且热敏电阻RX的功率不超过其额定功率1mW。
(2)式中,Ig=300×10-6A,Rg=160Ω,Rt=75=745.84Ω,因室温时微安表电流为零,电路为平衡电桥,所以Rs=Rt=25 ℃=5 000Ω,通过设置不同的R1=R2,可以得到不同的电源电压值(单位:V),如图3所示。因为要兼顾微安表的电流和温度的线性关系,后面需要对电源电压E和R1、R2值再进行选择优化。

(a) R1=R2=746 Ω时的电源电压

(b) R1=R2=2 500 Ω时的电源电压

(c) R1=R2=3 375 Ω时的电源电压
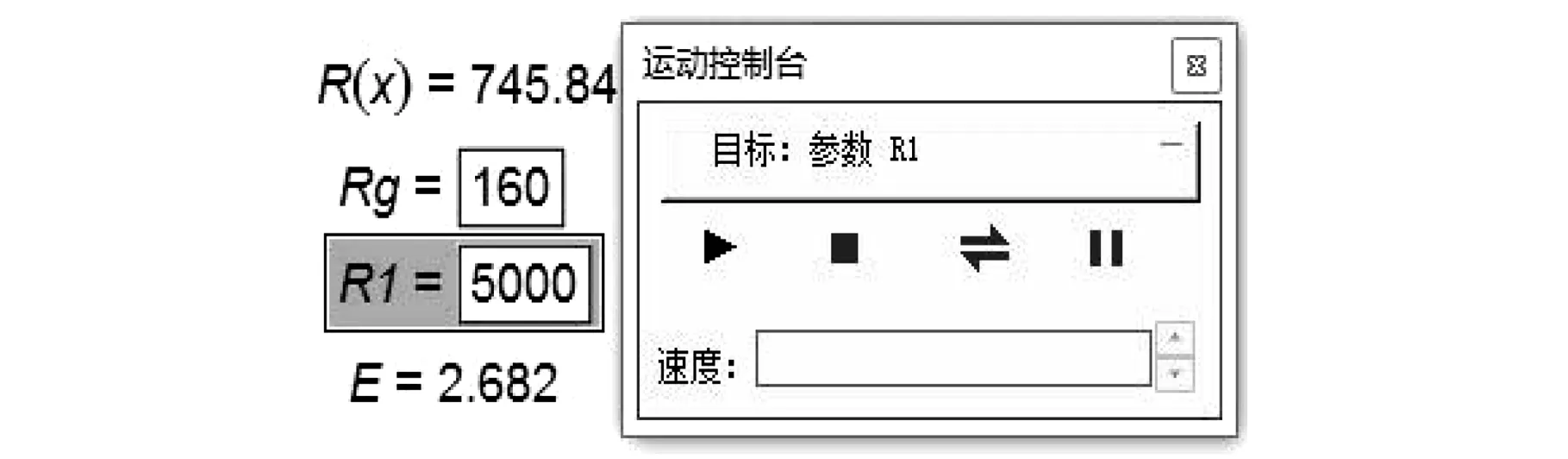
(d) R1=R2=5 000 Ω时的电源电压图3 电源电压分析
2.3 绘制微安表流过电流和热敏电阻温度的关系图
微安表流过的电流I(x)既是R(x)的函数,同时也是温度x的函数,如式(3)所示:
(3)
当温度x变化时,R(x)变化,I(x)的大小相应改变,可做出I-x关系图,如图4所示,AC间的曲线即为I-x关系图。可以看出,当温度在60.0 ℃~75.0 ℃时曲线线性较好,在40.0 ℃附近线性较差。之后会对此现象进行总结优化,得到线性关系最佳的参数。

图4 电流和温度的线性关系图
2.4 优化参数,得到最佳的温度和电流的线性关系
其它条件不变,改变R1=R2的大小,可以得到不同的电流和温度的关系曲线。如图5所示。AC间曲线是温度对应的电流关系图,直线是理想线性关系,AC间的曲线越接近直线,说明线性关系越好。图5a中R1=R2=746Ω时,线性关系最差;图5c中R1=R2=3 375Ω时,微安表流过的电流和温度线性关系最佳。
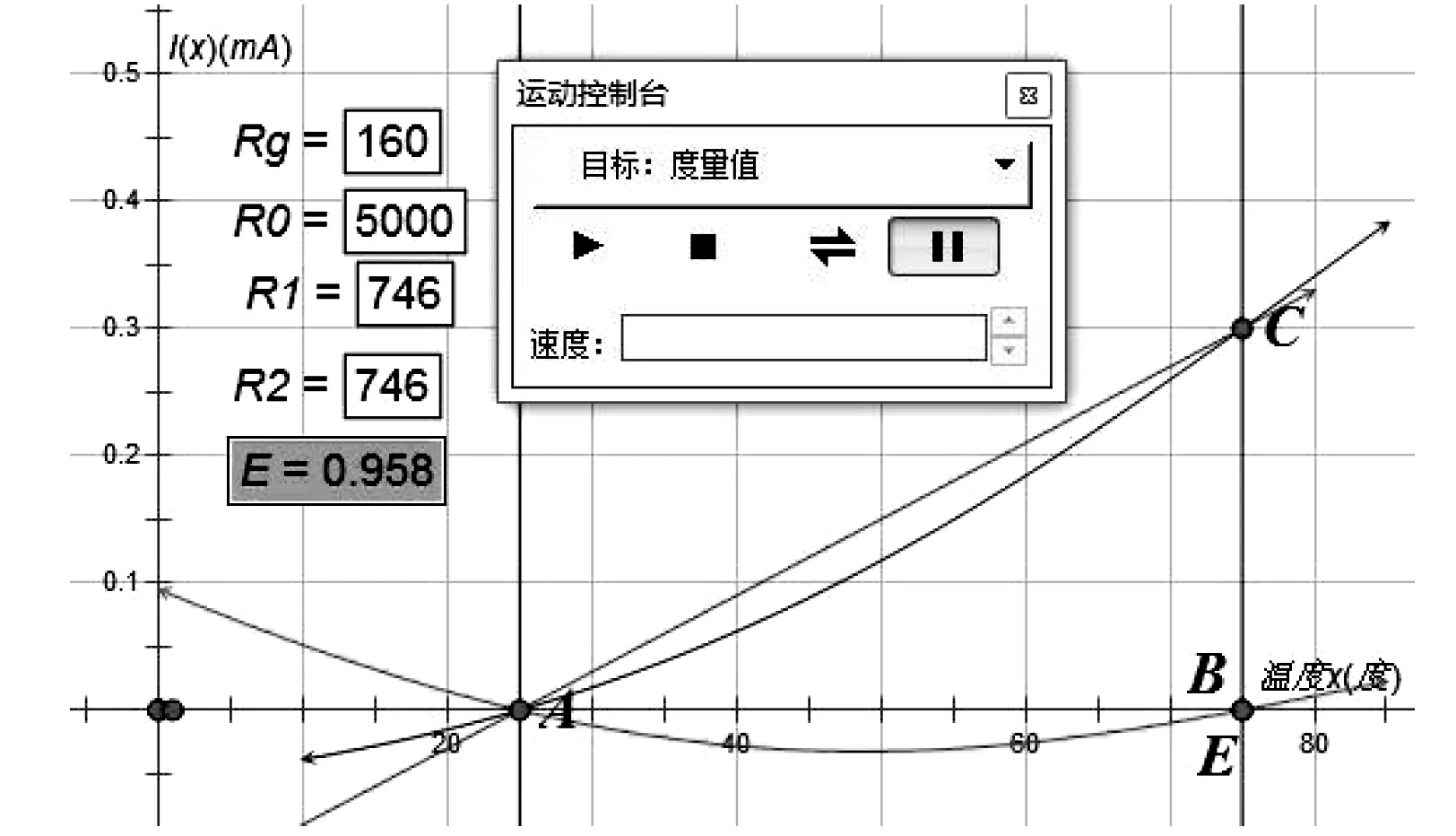
(a) R1=R2=746 Ω时,I-x关系图
与此同时,也可以用AEB曲线上的点和x轴的接近程度来表示线性关系,曲线AEB的纵坐标是AC间曲线和AC间直线纵坐标的差值,AEB越贴近x轴,说明线性越好。当E在AB中点时,此时线性关系最好,此结论和用上段AC线得到的相符:R1=R2=3 375Ω时,线性关系最佳。
综上所述,后续设计将以参数R1=R2=3 375Ω、E=2.009V为基础,进行计算或者验证。
2.5 计算热敏电阻上的实际承载功率
在实验的设计要求中,一项重要的指标就是热敏电阻上的功率不得超过1mW。热敏电阻上的功率计算公式为式(4)[10](单位:mW):
(4)
式中E、R1值固定不变,随着温度x的不同,热敏电阻上阻值和电流在变化,相应的功率P也在不断变化,如图6a所示。通过设置出温度x的取值范围,并点击“生成x参数的动画”,可动态得到热敏电阻在不同温度下的功率大小,如图6b、6c、6d所示。

(a) 热敏电阻功率与温度的关系图
当图1电路中的各元器件值确定后,即:E=2.009V、R1=R2=3 375Ω,Rs=5 000Ω,微安表内阻Rg=160Ω、微安表量程300uA时,可得到如图6的计算结果。在温度区间(25.0 ℃~75.0 ℃)观测热敏电阻功率随温度的变化数据,可知图6c参数下热敏电阻的功率达到峰值P(x)=0.434 8mW,远小于1mW,证明所设计的电路参数是安全的、非平衡电桥热敏电阻温度计的设计是成功的[11]。
3 结 语
文章用动态几何画板软件,逐步显示了电阻和温度的关系,完整模拟了“热敏电阻阻值大小与温度的关系”数据变化过程;当选择不同R1=R2的值,得到不同的温度和电流的关系曲线,择优选择参数为:E=2.009V、R1=R2=3 375Ω,微安表流过的电流和温度呈最佳线性状态;在最佳参数组合下,从25.0 ℃到75.0 ℃逐步地显示了每个温度下对应的热敏电阻的功率大小,最大功率0.434 8mW出现在58.0 ℃时,其值远小于1mW,说明设计参数可行且设计方案是合理的,达到了预期设计目的。
