电磁力互动柱塞泵电磁铁轴向位置优化研究

方磊，张洪信，赵清海，王东

(青岛大学 a. 机电工程学院; b. 动力集成及储能系统工程技术中心，山东 青岛 266071)

0 引言

电磁力互动柱塞泵的动力驱动结构为两个电磁铁，通过交互通断电实现衔铁-柱塞组件的往复移动，两个衔铁-柱塞组件之间通过同步齿轮联动[1-2]。电磁铁的轴向位置对整个电磁泵结构与性能影响巨大，这方面的研究亟待开展。

电磁铁轴向位置优化需要借助对电磁铁的仿真研究。这方面研究较早的有日本岐阜大学的OHOACHI Y等人使用Ansoft Maxwell电磁场仿真平台建立了电磁铁的仿真模型，深入研究了铁芯材料的磁化属性对电磁铁磁场的影响[3]，并通过分析后得出铁芯材料BH曲线、相对磁导率等参数会影响电磁铁的响应迟滞时间。北京理工大学的吴萌等人利用磁路分割法将电磁铁的磁路简化，建立电磁铁有限元仿真模型[4]，并对该电磁铁结构优化，优化后电磁铁的电磁力随激励电流变化特性曲线的线性度降低幅度较大，优化效果明显[5]。沈阳化工学院的张齐通过Ansoft Maxwell有限元仿真平台建立电磁铁的2D平台，研究了电磁铁的铁芯材料、铁芯吸合面形状等参数是如何影响电磁力的[6]。孙虎胆等人同样利用该仿真平台对电磁铁各个结构参数进行仿真，得到了电磁力的规律，提供了一种电磁铁仿真优化的方法[7]。袁洋、左才工等人以双行程螺管式电磁铁为研究对象，提出通过Ansoft Maxwell电磁仿真平台和ADAMS动力学仿真平台联合仿真的建模方法，得到了双行程螺管式电磁铁的静态特性曲线，并与实验结果对比，误差在允许范围内[8-10]。

虽然许多学者和科研机构都在进行电磁铁优化的相关工作，研究了电磁铁各个参数对电磁铁动力特性的影响，但是针对电磁力驱动往复柱塞泵的电磁铁性能分析与结构优化的相关研究还比较少，尤其是电磁铁在轴向位置的优化。

1 电磁铁轴向位置优化分析

研制的电磁力互动柱塞泵三维模型与样机如图1所示。

1—上支撑板；2—电磁铁；3—衔铁；4—柱塞；5—油缸；6—底座；7—齿轮轴；8—齿轮；9—齿条；10—侧支撑板。图1 电磁力互动柱塞泵三维模型与样机

衔铁的结构尺寸和上下运动行程固定，考虑电磁线圈在衔铁轴向位置的变化，利用COMSOL Multiphysics的AD/DC模块建立的电磁铁模型如图2所示。

图2 电磁铁三维模型

电磁铁的电磁线圈与衔铁工作行程的相对位置，决定了电磁力互动柱塞泵在工作时所利用的电磁铁输出特性曲线，即决定了电磁铁的有效输出。因此必定存在一个最优的电磁线圈位置，使电磁力互动柱塞泵在满足柱塞行程30 mm、工作无冲击的同时，输出最高的液压能以及尽可能减少电能消耗[11]。

当电磁铁线圈的轴向位置发生变化时，相当于衔铁的行程空间发生了相应变化，由前面仿真可知，影响电磁铁输出电磁力大小很大程度上取决于衔铁和电磁线圈的相对位置。为了方便仿真与优化，将线圈的轴向位置优化转化为选择最优的衔铁行程。电磁铁有效输出及衔铁行程示意图如图3所示。设计的电磁力互动柱塞泵的柱塞行程为35 mm，衔铁和柱塞连接在一起，因此衔铁的行程S=35 mm，即Sp-St=35 mm，其中St为衔铁行程起点，Sp为衔铁行程终点。设计的Pt-Pp段为14 mm，其中Pt为电磁线圈激励在半个周期内开始施加时的位移点；Pp为电磁线圈激励在半个周期内停止施加时的位移点。由电磁力互动柱塞泵的工作原理可知，St点和Pt点是重合的。

图3 电磁铁有效输出及衔铁行程示意图

由电磁力互动柱塞泵样机的电磁铁输出曲线可以看出，在柱塞行程开始时电磁力很小，仅42 N。随后因为衔铁的运动而使工作气隙减小，电磁力越来越大，电磁铁的有效输出仅为电磁力最小的那一段。因此，需要将电磁铁线圈的轴向位置重新配置，使得Pt-Pp段对应的电磁力为最大的一段，这样电磁力有效输出便能提高。在电磁力互动柱塞泵输出功率不变的前提下，提高了电磁铁的有效输出段，使通电时间大幅度下降，节省电能，提高能量转换效率。

在电磁力特性曲线已知的情况下，通过优化算法，便能得到最佳的Pt和Pp点[12]。

2 电磁铁轴向位置优化

2.1 优化模型

1)目标函数的确立

在衔铁行程St-Sp内，将柱塞的运动行程微分化，即将St-Sp平均分成1/deltx份，deltx为步长，当步长deltx趋向非常小的情况下，可以假设在每一个步长内将柱塞的运动简化为所受合力不变，也就是运动加速度不变，柱塞做匀加速运动，则在第k个步长内：

(1)

Femk=dis2F(S-disk)

(2)

(3)

(4)

(5)

式中：deltxk为时间步长，表示第k个步长内柱塞的运动时间；vk为第k个步长内柱塞速度的大小；Femk为第k个步长内电磁力大小；dis2F()为电磁力曲线的拟合函数；S为柱塞的行程，为35 mm；Ftk为第k个步长内互动齿轮对切向力大小；Ff1、Ff2为左右泵腔内流质对柱塞的作用力；Fμk为第k个步长内右柱塞所受摩擦阻力的大小；μ为柱塞与泵体之间摩擦系数，取0.06；ak为第k个步长内柱塞加速度的大小；m为单个柱塞的质量。

将式(2)-式(4)代入式(5)可求得在第k个步长内加速度ak，则目标函数vk为

vk=vk-1+deltxk×ak-1

(6)

为了方便表达，把目标函数记为min imize|vk|。

2)约束条件

g1: Σdeltx=35

柱塞运动到行程终点约束。

g2：vk=0

行程终点速度为0。

3)建立优化模型

根据对电磁力互动柱塞泵期望的运动状态，即要求柱塞在运动到上止点时速度为 0 为优化目标，以消除在上止点时的冲击。由上述确定的目标函数以及约束条件，该优化问题可描述为

min imize|vk|

s.t. g1: Σdeltx=35

g2:vk=0。

2.2 优化过程与结果分析

整个优化过程以上面的电磁力分析模型为学科分析工具，每一步优化迭代的电磁力都要调用该学科分析工具。

因为优化设计变量只有一个，这里选择序列二次规划法(NLPQL)。NLPQL算法将目标函数以二阶泰勒级数展开，并把约束条件线性化，通过解二次规划得到下一个设计点，然后根据两个可供选择的优化函数执行一次线性搜索。序列二次规划法(NLPQL)具有在涉及点局部进行快速搜索、对工程设计具有普遍的适用性、计算可以以并行的方式进行等优点[13-14]。

优化过程如图4所示。首先定义好初始值和相关参数输入给数值仿真模型，数值仿真模型根据所给参数确定电磁力特性曲线，通过仿真得到该参数下的电磁铁通电时间；数据记录模块将数值仿真的结果记录下来，然后将数据传递给优化模型，优化模型通过其优化算法规划出自变量下一个设计点并返回给数值仿真模块，如此循环直至找到满足约束条件下的最优解。迭代过程如图5所示。

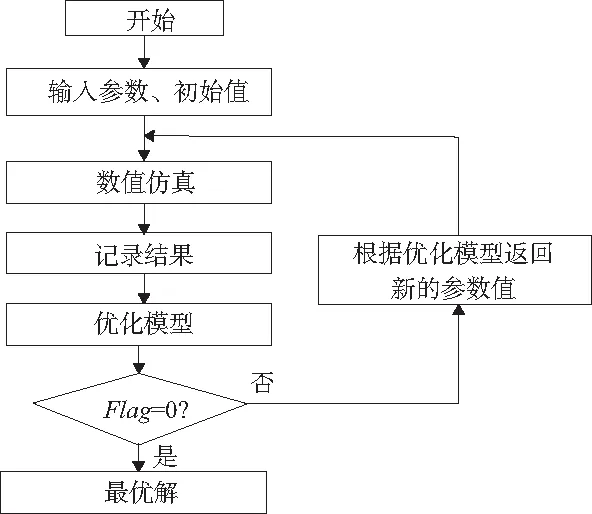
图4 优化模型示意图

图5 优化模型迭代过程图

最优迭代自变量St=33 mm，结合图3可知，St=38 mm时电磁铁电磁力最大，且此时衔铁与电磁线圈端面平齐；则优化后电磁线圈端面距离衔铁下止点的距离为5 mm，衔铁位于下止点时电磁铁的结构如图6(a)所示。图6是优化前与优化后衔铁位于下止点时电磁铁电磁线圈与衔铁位置的示意图。

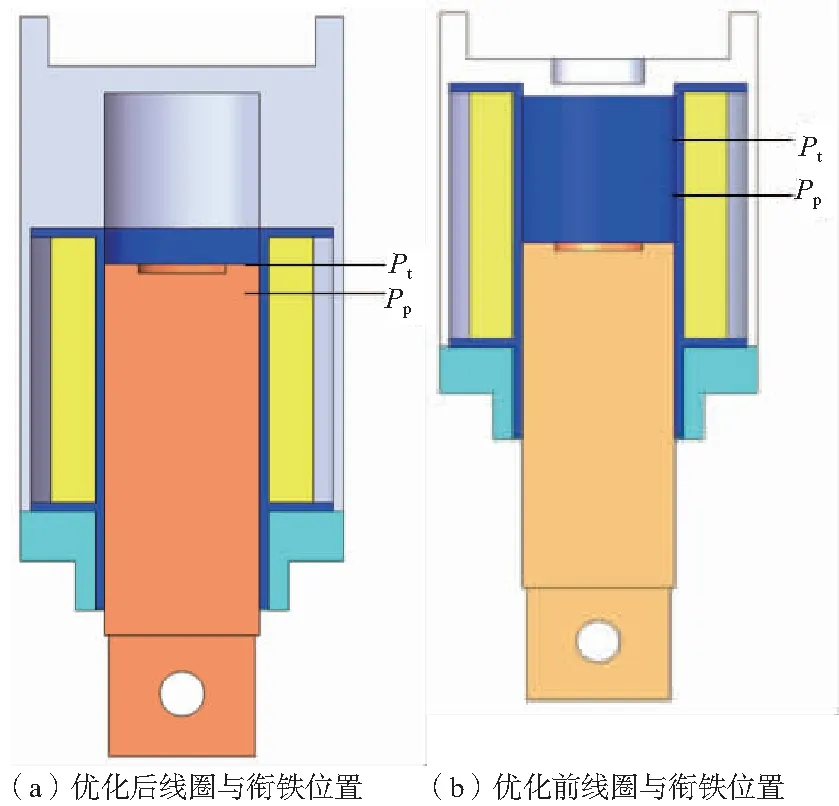
图6 电磁线圈与衔铁位置示意图

由图3可知，优化前Pt与Pp均位于最大电磁力位置的左侧，Pt到Pp这一段行程为14 mm，所对应的电磁力较小。优化后电磁力互动柱塞泵工作过程中的电磁力特性曲线如图7所示。优化后Pt与Pp位于最大电磁力位置的两侧，此时Pt到Pp这一段行程仅为4 mm，所对应的电磁力最大。故电磁铁轴向位置优化后一个周期内的线圈通电时间会缩短，电能消耗会降低，且通电时产生的电磁力会大幅提高。

比较图3和图7可以看出，优化前电磁泵的启动电磁吸力为42 N，优化后电磁泵的启动电磁吸力为160 N，增大了近3倍。这主要是对电磁铁高输出的电磁特性加以利用的结果。

图7 优化后电磁铁电磁力特性曲线

优化后衔铁运动速度随位移变化曲线如图8所示，衔铁运动速度随时间变化曲线如图9所示。由图可知：优化后当衔铁处于下止点时，线圈开始通电，当衔铁行程为9 mm时电磁线圈断电。此时线圈通电时间t=0.04 s，此后衔铁做匀减速运动，在行程终点S=35 mm时正好速度为0，行程终点时无冲击。对比优化前可知，半个周期内电磁线圈通电时间由优化前的0.07 s降低到了0.04 s，电能消耗降低了43%。

图8 优化后衔铁运动速度随位移变化曲线

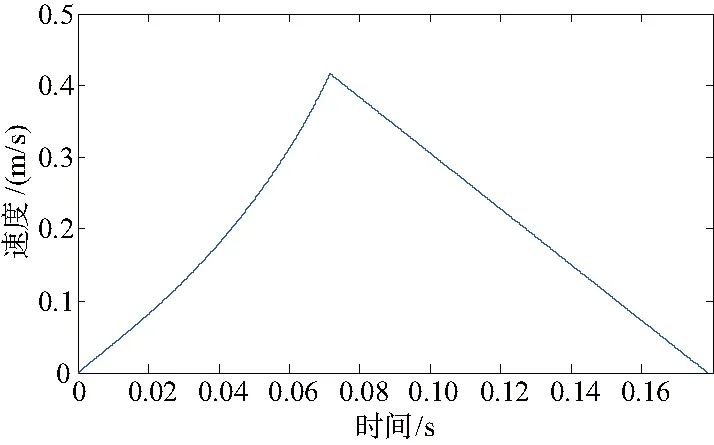
图9 优化后衔铁运动速度随时间变化曲线

3 结语

为充分利用电磁铁输出特性曲线的高输出段，提高电磁泵的工作效率，基于COMSOL低频电磁场平台建立电磁铁的有限元仿真模型，得到衔铁轴向位移的电磁力特性曲线。根据得到的电磁力特性曲线以线圈轴向位置为设计变量建立优化模型，通过优化，得到最优的线圈轴向位置。优化后，电磁力互动柱塞泵的能量转换效率提高了43%，启动电磁吸力增大了近3倍。