内压碟形封头塑性垮塌压力预测方法
2021-05-21唐保威
唐保威,徐 平
(浙江大学 应用力学研究所,杭州 310027)
0 引言
碟形封头是压力容器常见的部件,在石油、机械、化工、航空航天等领域有广泛应用。因其使用环境复杂,为保障安全,碟形封头的壁厚设计一般偏大,但这造成了材料浪费,增加了制造成本[1-3]。塑性垮塌失效是内压碟形封头设计需要考虑的重要失效模式,精准预测塑性垮塌压力有助于设计碟形封头时,在避免塑性垮塌的前提下减少用料,因此具有重要意义。
陆明万等[4-9]介绍了基于材料硬化的真应力-真应变本构模型分析垮塌载荷的塑性分析方法,指出塑性分析方法的计算结果更为精确。ZHENG等[10-11]采用基于弧长法的非线性有限元技术,考虑实测的材料应力-应变曲线,预测一个与筒体焊接的冷冲压标准碟形封头塑性垮塌压力,预测结果与试验结果吻合好;用该方法探究了椭圆封头各项参数对塑性垮塌压力的影响,归纳出了椭圆封头塑性垮塌压力的预测公式,与试验结果吻合良好。然而,基于有限元的数值模型要付出较大的计算工作量,过程更费时[4-7]。理论分析方面,UPDIKE等[12]将碟形封头支撑环以上部分等效为球冠,基于von Mises各向同性硬化模型和大变形理论,采用Hill应变假设[13]推导公式计算了碟形封头的塑性垮塌压力,但其公式需要迭代计算,且支撑环半径仍需采用有限元分析获取,该方法无法独立使用。
目前针对碟形封头塑性垮塌压力预测方法仍缺少深入系统的研究。本文从有限元分析、理论计算、试验验证三方面对该问题进行研究。首先,采用基于弧长法的非线性有限元技术,建立考虑应变硬化的碟形封头塑性垮塌压力预测数值模型;然后,在文献[12]的研究基础上,推导出可以独立使用的碟形封头塑性垮塌压力计算公式,并将公式计算与有限元分析相互对比,以验证预测方法的可靠性;最后,结合不同尺寸、材料和制造工艺的碟形封头爆破试验数据,对预测方法的准确性进行验证分析。
1 有限元法
1.1 模型建立
利用ANSYS对内压碟形封头的塑性垮塌压力进行有限元分析预测。工程上,碟形封头通过法兰与筒体连接,或直接与筒体焊接。以BLACHUT[14]试验中的K3封头(法兰连接,见图1)和MILLER等[15]试验中的CBI1封头(筒体焊接,见图2)为例进行有限元分析,封头的尺寸参数如表1所示。
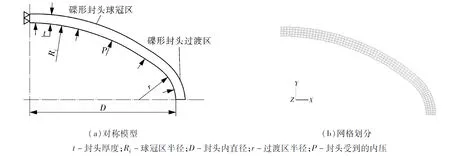
图1 K3封头的对称模型和网格划分示意
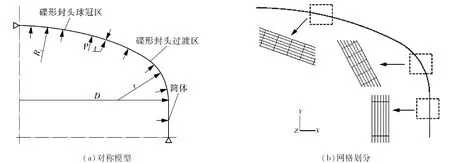
图2 CBI1封头的对称模型和网格划分示意
建模时,由于碟形封头在内压下的几何结构、载荷具有轴对称特征,故建立轴对称模型;采用Plane 182单元划分网格;通过法兰与筒体连接的封头,在封头顶部对称轴线施加X方向的位移约束,封头底部施加位移全约束;直接与筒体焊接的封头,在封头顶部对称轴线施加X方向的位移约束,在筒体底部施加Y方向的位移约束。
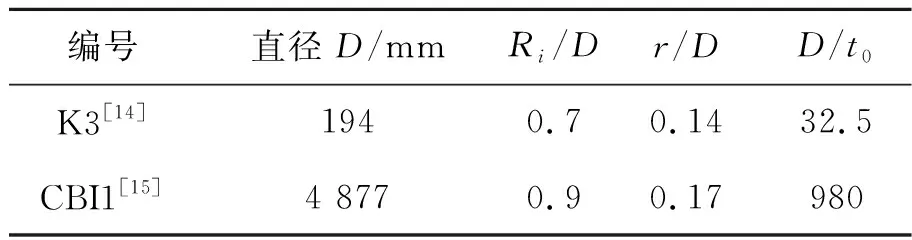
表1 碟形封头尺寸参数
材料模型采用真应力-真应变曲线(见图3[14-15])。其中K3封头模型采用BLACHUT[14]实测的真应力-真应变曲线。CBI1封头则根据MILLER等[15]实测的材料弹性模量、屈服强度、抗拉强度的平均值,利用ASME BPVC Ⅷ.2—2019附录3-D的本构关系确定其真应力-真应变曲线。
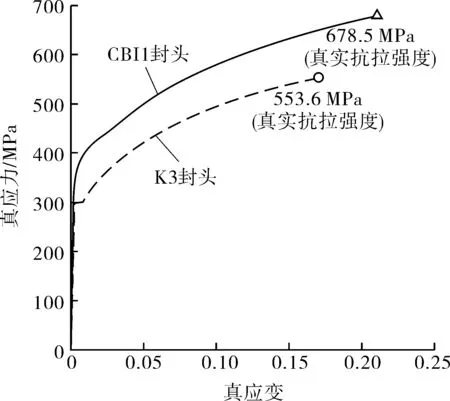
图3 真应力-真应变曲线
1.2 计算结果
(a)压力-应变曲线
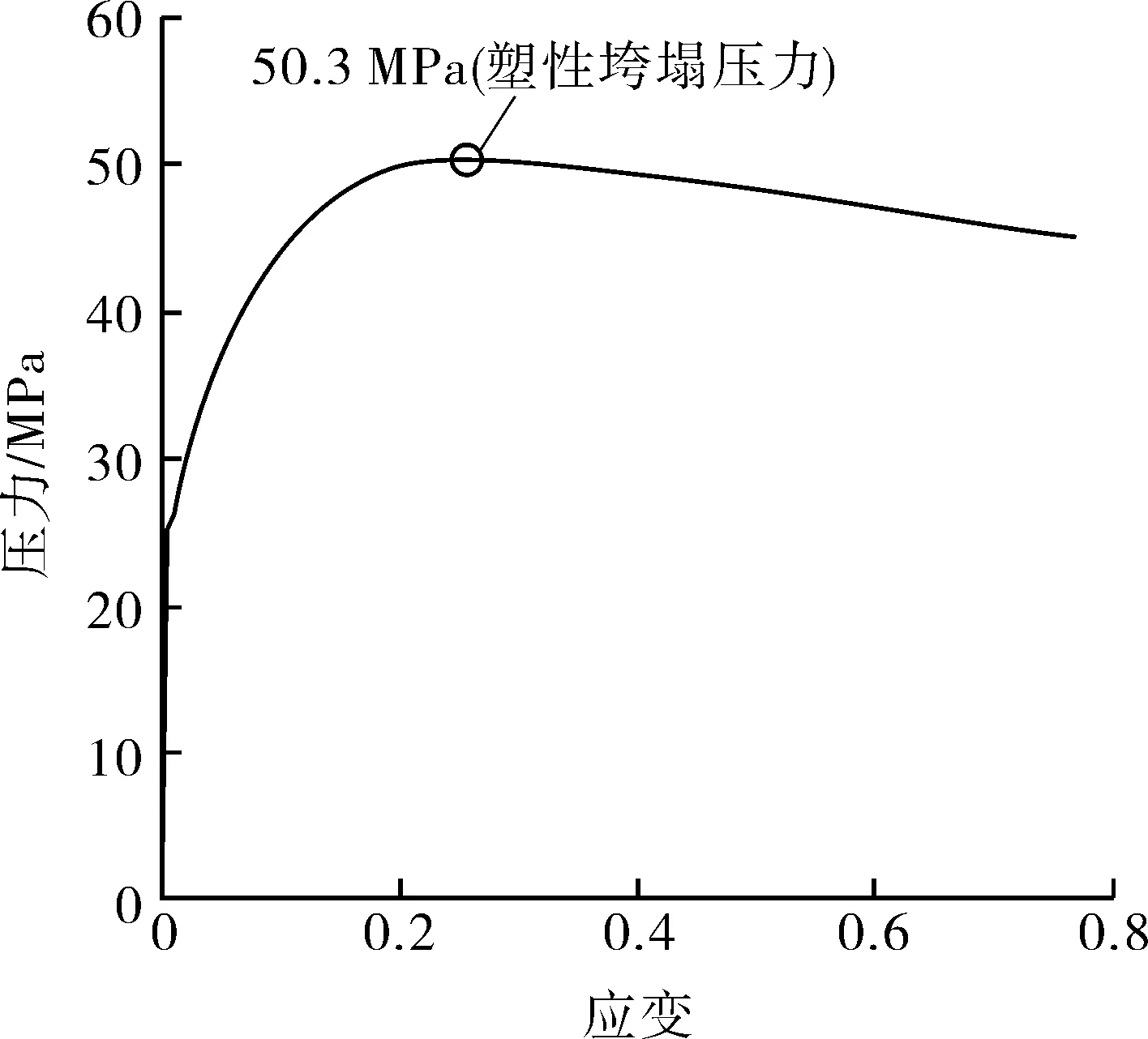
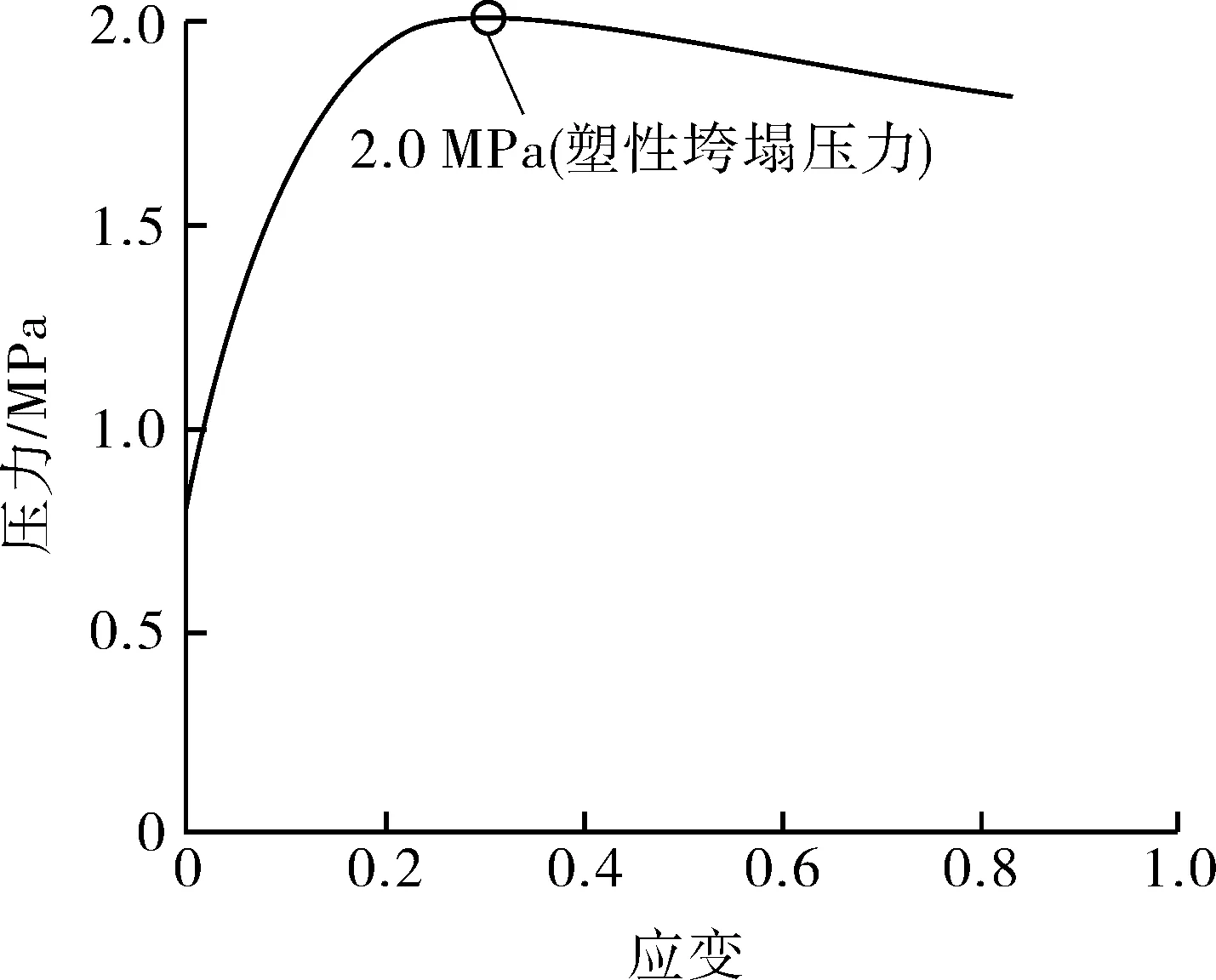
采用基于弧长法的非线性有限元技术进行计算,弧长法可自动调整弧长增量,当曲线结构表现出非线性特征时,弧长会自动减小,迭代增多,故能很好地跟踪压力-应变曲线的突变点[16]。获得K3和CBI1封头模型在封头顶点位置的压力-von Mises应变曲线见图4(a),5(a)。
(a)压力-应变曲线
由塑性垮塌的定义可知塑性垮塌压力是结构能够承载的最大压力[4],表现在“压力-应变”图像上即为曲线的最高点,故K3封头和CBI1封头的塑性垮塌压力分别为50.3 MPa和2.0 MPa,两者在塑性垮塌压力下的等效塑性应变云图如图4(b)和图5(b)所示。
2 理论方法
2.1 理论基础
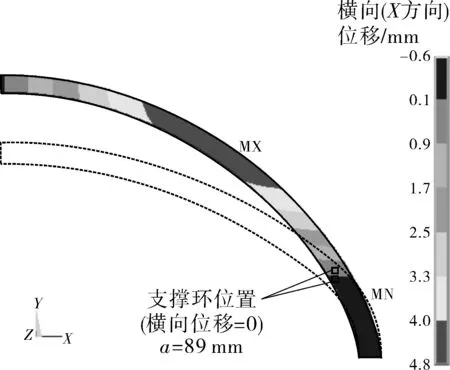
由有限元计算结果可以看出,内压作用下碟形封头球冠区向外变形,过渡段向内变形,因此碟形封头在变形前后存在环向应变为零(横向位移为零)的位置,见图6。UPDIKE等[12]曾将环向应变为零位置及以上部分的封头等效为具有支撑环的球冠(即将图6中箭头所指向的记号以上的封头等效为图7的模型),并基于Hill应变假设[13],计算内压碟形封头塑性垮塌压力。
(a)K3封头
公式推导在下列假设下进行:(1)工程上碟形封头径厚比大于10,认为封头处于膜应力状态;(2)等效球冠在变形中各处曲率始终保持一致,即等效球冠始终为球状;(3)Hill应变假设[13](等效球冠顶点附近的微元的瞬时路径与等效球冠轮廓截面垂直);(4)碟形封头所用材料大多为金属,适用幂指数本构模型,且由于金属材料的弹性段对塑性垮塌压力几乎没影响,采用Swift本构关系;(5)材料不可压缩。
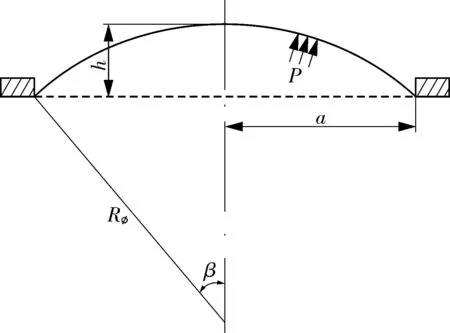
图7 等效球冠模型示意
根据图7可以得到几何关系:
h=Rφ(1-cosβ)
(1)
a=Rφsinβ
(2)
(3)
式中,h为等效球冠的高度,mm;Rφ为等效球冠的曲率半径,mm;β为等效球冠球心和支撑环连线与对称轴的夹角,(°);a为等效球冠半径(支撑环半径),mm。
Mises等效应力和等效应变:
σe=σθ=σφ
(4)
εe/2=εθ=εφ=-εz/2
(5)
式中,σe为Mises等效应力,MPa;σθ为环向应力,MPa;σφ为经向应力,MPa;εe为Mises等效应变;εθ为环向应变;εφ为经向应变;εz为法向应变。
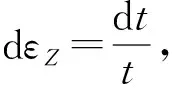
t=t0exp(εZ)=t0exp(-εe)
(6)
根据Hill应变假设[13]:
(7)
式(5)(7)积分得到:
(8)
Swift本构模型[12]:
σe=C(b+εe)n
(9)
式中,C,b,n为Swift本构关系的材料参数。
薄膜理论:
(10)
2.2 本构关系
Swfit本构关系中的材料参数C,b和n可以通过下式[12]计算:
n=b+ln(1+eu)
(11)
su(1+eu)=C[b+ln(1+eu)]n=Cnn
(12)
sy(1+ey)=C[n-ln(1+eu)+ln(1+ey)]n
(13)
联立式(11)~(13)可得到n的非线性方程:
(14)
式中,e为工程应变;ε为真应变;s为工程应力,MPa;σ为真应力,MPa;下标y为屈服点;下标u为抗拉强度点。
由式(14)首先求得n,进而得到b和C。其中,屈服强度对应的工程应变ey=sy/E。对于抗拉强度的工程应变eu,可以先确定屈强比K(K=sy/su),采用ASME BPVC Ⅷ.2—2019附录3-D的本构关系确定真应变εu(见式(15)),再按工程应变与真应变关系ε=ln(1+e)计算eu。
(15)
由此,获得K3封头所用的材料参数C,b和n分别为750,0.002 5,0.172 9;CBI1封头所用的材料参数C,b和n分别为945,0.010 3,0.217 3,对应的Swift真应力-真应变曲线见图8。
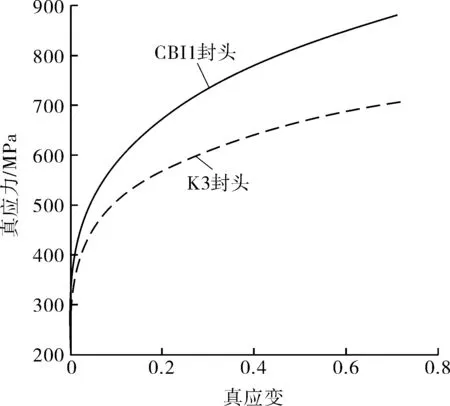
图8 K3封头和CBI1封头的Swift曲线
2.3 塑性垮塌压力
塑性垮塌压力是结构能够承载的最大压力,表现在“压力-应变”图像上即为曲线的最高点,故封头塑性垮塌条件[17]:
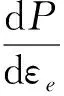
(16)
为求得封头塑性垮塌压力,避免迭代运算,需进一步获得封头所受压力与等效应变的关系式。联立式(3)(5)(7),得等效球冠的高度:
(17)
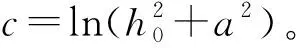
联立式(3)(6)(10)(17),即可得封头所受压力P:
P=4t0σe[exp(-c-2.5εe)
-exp(-2c-3εe)a2]1/2
(18)
结合式(9)和式(18),得封头所受压力P与等效应变εe的关系式:
P=4t0C(b+εe)n[exp(-c-2.5εe)
-exp(-2c-3εe)a2]1/2
(19)
利用式(19)可将封头所受压力P与等效应变εe绘制出关系曲线(见图10),可知曲线上最高点的压力为塑性垮塌压力。
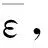
(20)
对式(9)求导并与式(20)比较得:
(21)
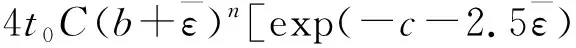
(22)
式(22)可以直接求得碟形封头的塑性垮塌压力。对于一个确定的封头,t0,C,b,n,c,a均为常量,其中a只是理论上的概念,如何获得a是下一步计算的关键。
主要考虑D,Ri,r,sy,su对a的影响,记Ri/D=m,r/D=l,引入强度常数Q=100 MPa对sy和su进行无量纲处理,记sy/Q=syQ,su/Q=suQ。希望得到a=f(D,m,l,syQ,suQ)的表达式,为此利用有限元对不同条件下a的值进行仿真分析。尺寸方面考虑欧盟规范EN 13445-3UnfiredPressureVessel、ASME规范ASME BPVC.Ⅷ.2—2019Rulesforconstructionofpressurevessels,division2,alternativerules和我国GB/T 150—2011《压力容器》中关于m,l的规定,在D=200~5 000 mm,m=0.7~1.0,l=0.05~0.35范围内进行有限元仿真;材料的sy,su则参考GB 713—2014《锅炉和压力容器用钢板》中常见牌号的sy和su,并为了研究规律适当扩大范围,取sy=230~650 MPa,su/sy=1.1~2.6。仿真结果显示a和D,m,l,syQ,suQ存在着极强的规律性。将所有仿真结果用SPSS(Statistical Product and Service Solutions)软件进行非线性回归,选择Levenberg-Marquardt方法对回归参数进行最小二乘估计,得到:
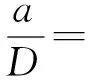
-0.011syQ+0.008suQ
(23)
该式可以在D=200~5000 mm,m=0.7~1.0,l=0.05~0.35,sy=230~650 MPa,su/sy=1.1~2.6的范围内使用。将仿真得到的a与公式计算得到的a对比,如图9所示,两者平均误差仅为-0.14%,标准差为1.94%。式(23)可以独立于有限元获得支撑环半径a的值,使本节得到的理论公式具备了使用价值。
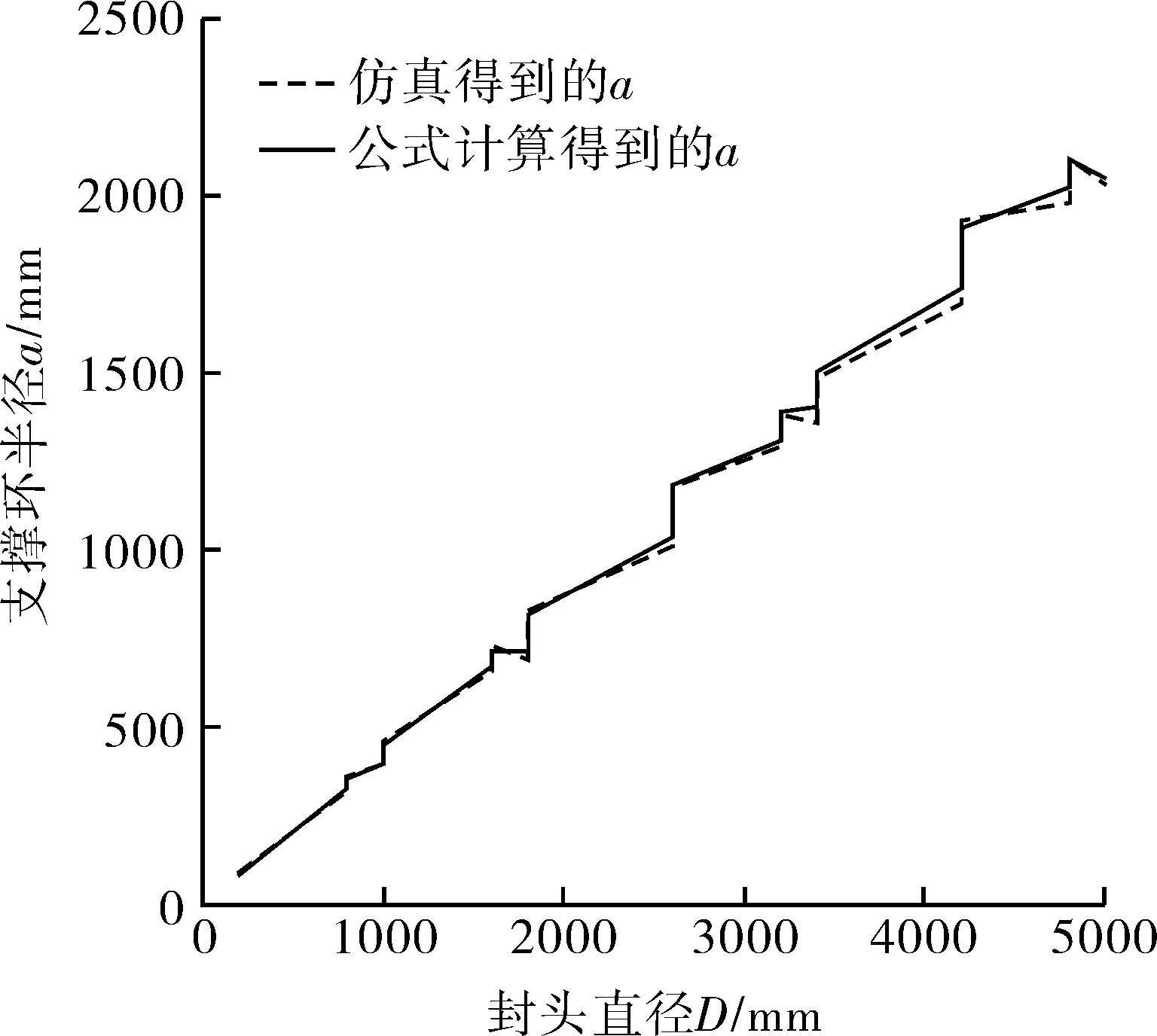
图9 仿真得到的a与公式计算得到的a的比较
K3封头模型和CBI1封头模型等效球冠半径a(以内径为基准)、材料参数C,b和n见表2。图10示出了K3封头模型和CBI1封头模型的压力-等效应变曲线,从而得到K3封头和CBI1封头模型的塑性垮塌压力分别为53.44和2.15 MPa。

表2 等效球冠参数
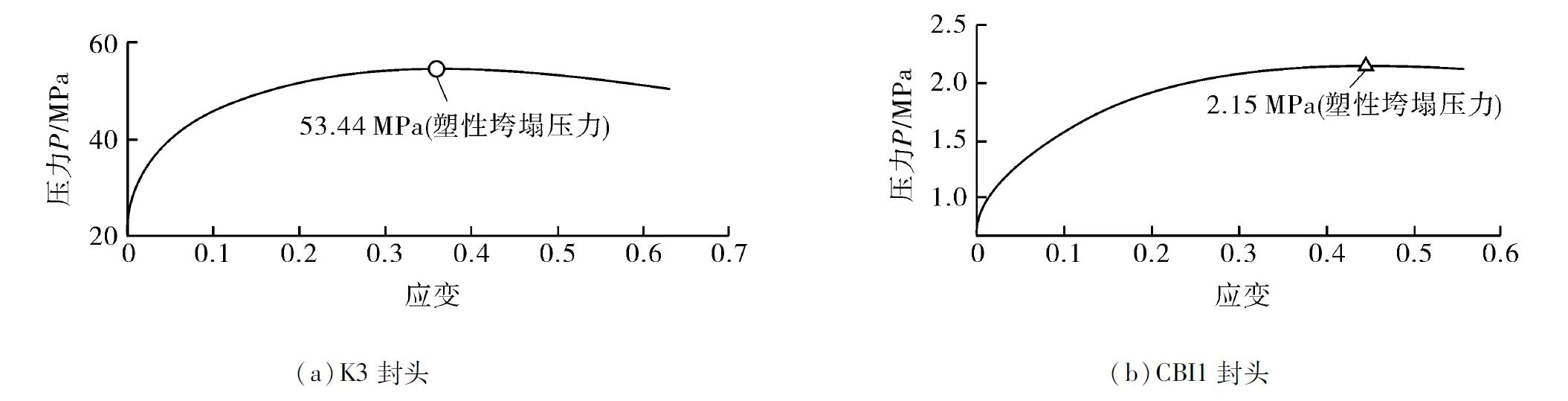
图10 K3和CBI1封头的塑性垮塌压力
3 试验验证
为验证碟形封头塑性垮塌压力预测的有限元法和公式计算法,从文献中查阅总结16个碟形封头的爆破试验数据,见表3。对表中的碟形封头分别按第1章的预测模型和第2章的公式法计算塑性垮塌压力的有限元解和公式解,并与封头爆破压力试验值进行比较。
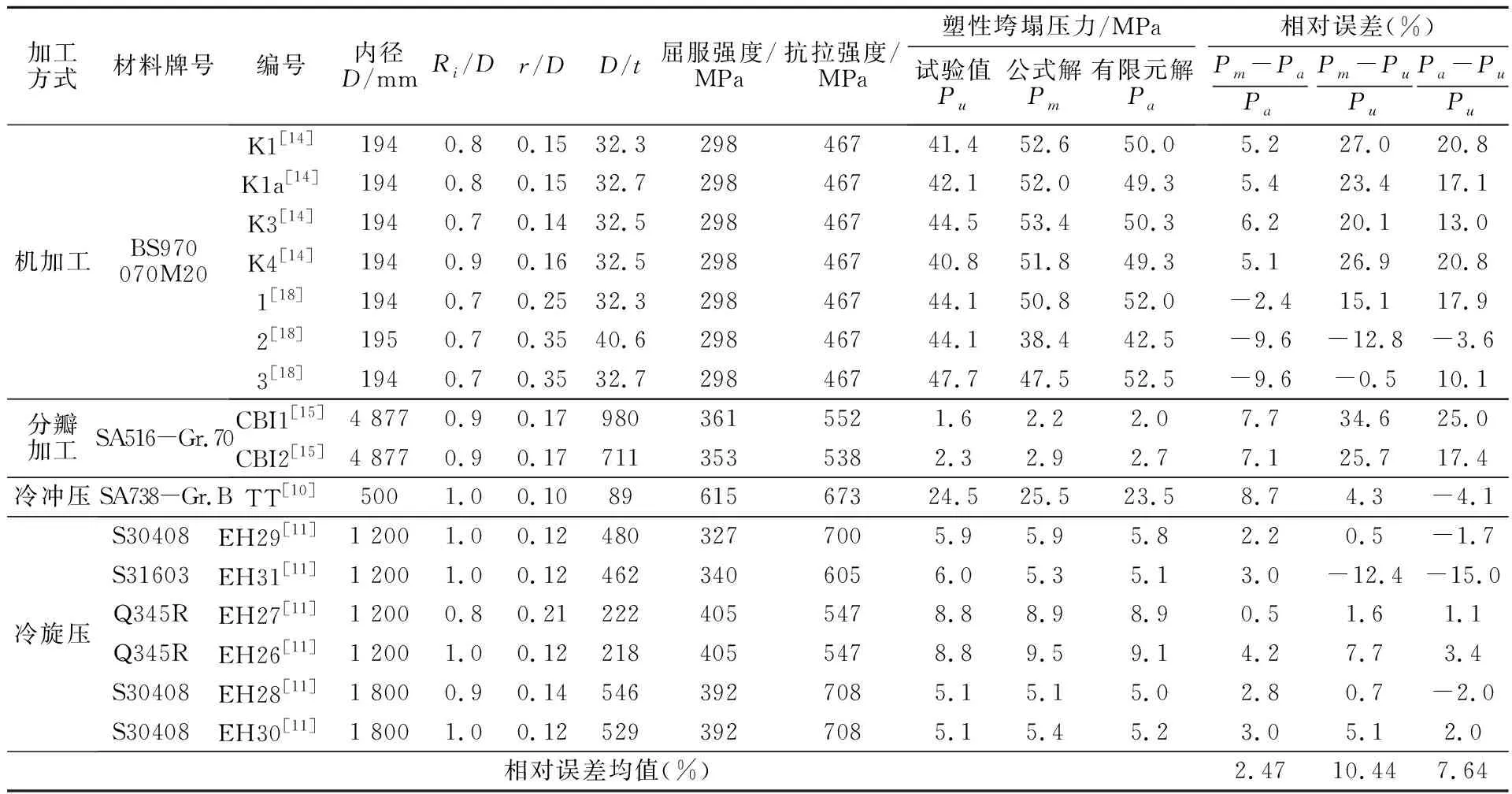
表3 碟形封头试验数据汇总及误差对比
从表3可以看出,碟形封头塑性垮塌压力的有限元解与公式解的相对误差范围为-9.6%~8.7%,平均误差仅为2.47%,表明碟形封头塑性垮塌压力的有限元解与公式解的吻合程度很高,验证了本文预测方法的可靠性。且公式法只需知道碟形封头的D,Ri,r,t0,sy,su,便可完成计算,效率远高于有限元,当面临大量碟形封头需要预测其塑性垮塌压力时,公式法无疑会是一种便捷、高效的方法。
Blachut系列封头(编号为K),有限元解比试验值高20%左右,公式解比试验值高20%以上。该系列封头采用钢锭机加工制造,而钢锭中心存在缩孔残余,即封头顶部存在缩孔缺陷,导致试验封头承载性能大大降低[14,19]。另3个Blachut系列封头(编号为1,2,3)的缩孔缺陷相对较小,有限元解、公式解均与试验值吻合较好。CBI系列封头分瓣加工,封头存在较多焊接接头,且CBI1封头在过渡段焊缝处破裂、CBI2封头破口平行于球冠拼焊缝,在焊接接头热影响区破裂,导致分瓣加工的封头爆破压力试验值低于有限元解和公式解。对于冷冲压和冷旋压的封头,封头质量较高,塑性垮塌压力的有限元解、公式解与试验结果吻合良好。总体来说,碟形封头塑性垮塌压力的有限元解、公式解与试验值吻合良好,验证了碟形封头塑性垮塌压力有限元计算和计算公式在理想条件下的准确性。
4 结论
(1)采用基于弧长法的非线性有限元技术,建立了考虑应变硬化的碟形封头塑性垮塌压力有限元预测数值模型。推导出碟形封头塑性垮塌压力的公式计算方法,并使之能够独立使用。碟形封头塑性垮塌压力的有限元模型和公式计算的预测结果吻合良好,表明预测方法可靠。
(2)汇总了16个不同碟形封头爆破试验数据。公式法、有限元法计算结果与试验结果吻合良好,验证了碟形封头塑性垮塌压力的有限元计算和公式计算在理想条件下的准确性。为建立考虑材料应变硬化的、防止碟形封头塑性垮塌的设计方法提供技术支撑。
