喷油润滑工况下可倾瓦推力轴承推力瓦热变形研究
2021-05-21李永海孙向志武鼎超
李永海,沈 健,孙向志,马 珅,武鼎超
(1.哈尔滨理工大学 机械动力工程学院,哈尔滨 150080; 2.中国船舶重工集团公司第703研究所,哈尔滨 150078 )
0 引 言
可倾瓦推力轴承在船舶推进轴系中具有广泛的应用,其需要完成将船舶推进器产生的轴向力传递给船体的工作,作为机组的“心脏”部件,其工作性能的优劣,直接影响它的效率及可靠性[1]。随着船舶总体性能的提高,推进轴系的推力负载随之增大,推力轴承的结构尺寸也将显著增大[2]。
可倾瓦推力轴承稳定运行过程中,镜板会带动润滑油运动,当润滑油流经由镜板和推力瓦面形成的楔形间隙时会产生动压效应,对轴系起到轴向支承作用[3]。由于镜板的高速运动会使油膜产生大量的摩擦热,这些热量会导致推力瓦产生热变形[4]。实验表明,推力瓦的热变形会达到与油膜厚度同一个数量级,严重时会导致油膜难以维持,产生油膜破裂现象使得推力瓦与镜板直接接触并产生烧瓦事件[5-8]。
可倾瓦推力轴承的润滑方式分为浸油润滑和喷油润滑。浸油润滑工况下,推力轴承的推力瓦始终浸没在油池内,靠镜板将油池内润滑油带入楔形间隙从而形成有效润滑油膜;喷油润滑工况下,喷油嘴将润滑油直接喷射在镜板上,再由镜板带入楔形间隙。目前对推力瓦的研究大多基于浸油润滑工况,对喷油润滑工况下的推力瓦研究较少,本文将分析喷油润滑工况下推力瓦的热变形情况。为此,作者先用Fortran语言编写的润滑计算程序对油膜温度场进行数值求解,再利用ANSYS进行推力瓦三维建模并对推力瓦热变形进行数值仿真求解。
1 数学模型建立
可倾瓦推力轴承实际运行时,有诸多因素会对其工作性能产生影响且情况复杂,若全部考虑会使得计算量增加并导致模型可求解性降低,因此本文做出如下假设:
1)润滑油的流动为层流且其与推力瓦表面不产生滑移现象;
2)推力轴承在稳定运行时,油膜厚度在几十微米范围内,可认为在膜厚方向上压力值、温度值保持不变,这样可以将数值求解得到的油膜压力场和温度场施加在推力瓦模型表面;
3)推力瓦材料为钢基,表层浇铸有巴氏合金,为简化计算,将推力瓦看作理想弹性体,即推力瓦满足连续性、完全弹性、各向同性、均匀性4个条件;
4)忽略推力瓦表面粗糙度以及平面度的影响;
5)不考虑镜板的受热变形以及受力变形;
6)润滑油的比热容、体积膨胀系数、导热系数均为常数;
7)忽略推力轴承安装误差,即各个推力瓦均匀受力。
1.1 油膜温度场计算
油膜温度来源于油膜的剪切和压缩产生的摩擦热,通过联立雷诺方程、能量方程、油膜形状方程、热油携带方程、粘温方程并对其进行数值求解来确定某一工况下推力瓦瓦面的油膜温度场[9-12]。
1.2 导热方程
与推力瓦上表面相对运动的镜板做匀速圆周运动,在推力瓦内无其他热源,可视作稳态导热,根据傅里叶定律可建立导热微分方程:
(1)
式中:a为导温系数,m2/s。
推力瓦上表面与油膜相接触,有稳定的热源;推力瓦另五个面则为对流换热边界。
1.3 固体热弹性变形方程
固体的热弹性变形采用有限元法进行数值分析;通过运用ANSYS软件对推力瓦三维结构进行静力分析;然后基于弹性力学理论,通过求解平衡方程组来求解推力瓦各节点位移量,以下为平衡方程组:
[K]{U}={R}
(2)
式中:[K]为结构刚度矩阵;{U}为节点位移向量;{R}为温度载荷向量。
2 推力瓦建模及其边界条件处理
2.1 推力瓦三维建模
本文的研究对象为中心点支承扇形可倾瓦推力轴承,并在workbench DM模块中进行三维建模,推力瓦表面划分印记面用来对推力瓦施加温度载荷,如图1所示。
2.2 油膜温度场处理
本文需要将Fortran语言程序联立方程求解所得的温度场施加在推力瓦瓦面,用来计算推力瓦体的温度分布以及热变形。而Fortran程序输出49个节点的温度值,会降低求解精度,因此使用三次样条插值的方法人为加密网格节点,使之成为169个节点,如图2所示。

图1 推力瓦三维模型Fig.1 model of thrust tile

图2 网格节点Fig.2 grid nodes
2.3 边界条件
热传递的方式有热传导、热对流和热辐射3种方式。可倾瓦推力轴承在稳定运转过程中属于稳态导热问题。稳态导热问题的边界条件有3种,分别为第一类边界条件、第二类边界条件、第三类边界条件。第一类边界条件规定了边界上的温度值;第二类边界条件对边界上的热流密度做了规定;第三类边界条件则对物体边界上和周围流体间的表面传热系数和温度等进行规定[13-16]。
推力瓦瓦面与油膜相接触,稳态运行时油膜温度场恒定并直接作用于推力瓦瓦面,属于第一类边界条件。推力瓦四侧表面上附有一层从上瓦面溢出向下流动的润滑油,其温度由上瓦面边缘温度决定并与推力瓦侧表面进行对流换热;推力瓦底部表面则看作与空气进行自然对流换热,这些表面都属于第三类边界条件。
对流换热系数可以通过努谢尔数来进行计算,其中的公式可表示为:
(3)
式中:h为表面换热系数;Nμ为努谢尔数;λ为流体导温系数;L为对流换热面积,m2。
经实验研究,自然对流换热的努谢尔准则数方程为:
Nμ=C(GrPr)n
(4)
可倾瓦推力轴承在喷油润滑方式下其四周边界可看作竖壁面对流换热情况,上述公式中的常数根据经验公式取值为C=0.59、n=0.25,根据晓格拉夫数和普朗特数计算公式,上述公式又可写作:
(5)
式中:μ为流体流速,m/s;Cp为流体的比热容,kJ/(kg·℃);av为流体的体积热膨胀系数;ν为流体运动黏度,m2/s。
3 推力瓦热变形仿真及结果分析
仿真所用参数:推力瓦内径320 mm、推力瓦外径620 mm、瓦张角为40°、支承位于推力瓦中心、瓦厚为40 mm、平均周向线速度为22.88 m/s、润滑油型号为46#透平油,且保持喷嘴处入油温度恒定。本文将分析喷油润滑条件下2、3、4、5、6 MPa不同比压工况时推力瓦的受热变形,并与相同结构、相同工况、浸油润滑条件下推力瓦的受热变形进行比较。
推力瓦稳定运转时其温度场稳定,为了将温度场施加在推力瓦表面上,须将计算出来的169个节点换算成144个面温度并设置为推力瓦上表面印记面上,如图3所示,其中推力瓦的左边为入油边,右边为出油边。
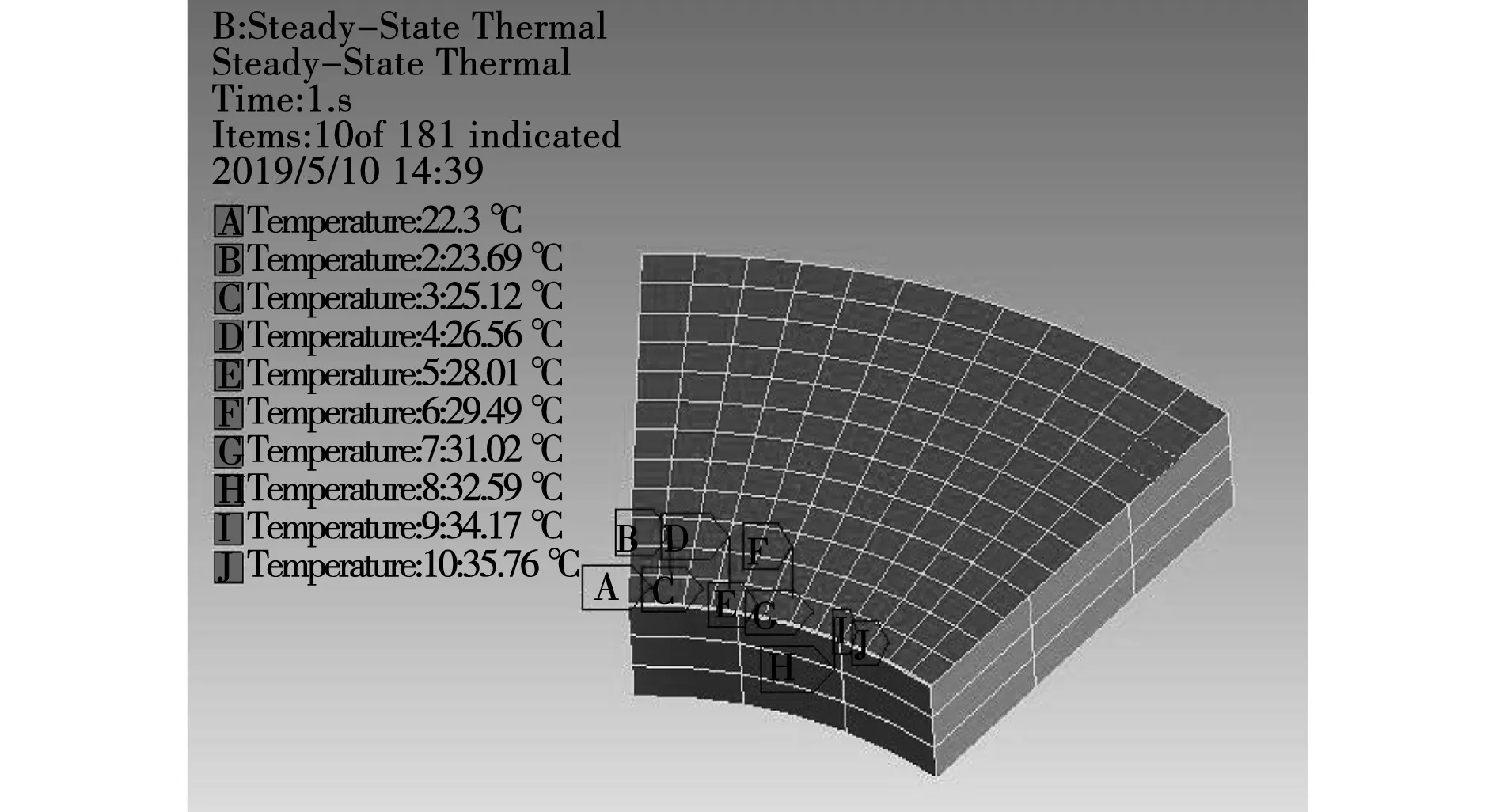
图3 推力瓦表面温度施加Fig.3 surface temperature applied
推力瓦侧表面施加由计算努谢尔数所得的对流换热系数,底面则设置为与空气进行对流换热。
利用ANSYS软件对推力瓦进行有限元分析,得到结果为推力瓦的整体变形情况,而要得到推力瓦的挠度变形,需要对仿真结果进行一定的后处理,忽略周向和径向的变形,仅保留推力瓦瓦面沿瓦厚方向的变形情况,最终得到推力瓦变形云图,如图4所示。

图4 喷油润滑工况下推力瓦热变形量云图Fig.4 thermal deformation cloud diagram
由图4可以看出喷油润滑工况下推力瓦变形为中间凸起的凸变形,沿瓦厚方向变形从左到右逐渐增大,变形最大处靠近出油边。随着比压从2 MPa增大到6 MPa,推力瓦的热变形也随之增大,总体变形趋势保持不变。
在浸油润滑工况下,推力瓦整体浸没在油池中并且保持油池的温度恒定为22°。利用ANSYS软件对推力瓦进行有限元分析,得到浸油润滑工况下推力瓦上表面沿瓦厚方向的变形云图,如图5所示。

图5 浸油润滑工况下推力瓦热变形量云图Fig.5 thermal deformation cloud diagram
由图5可以看出浸油润滑工况下推力瓦由热变形产生的挠变形形状与喷油润滑工况的变形相似,整体为四边向下弯曲变形。随着比压从2 MPa到6 MPa,推力瓦的变形也随之增大。
推力瓦的挠度变形量为推力瓦沿瓦厚方向变形最高点与最低点之间的差值,两种不同润滑方式工况下最大挠度变形量如图6所示。
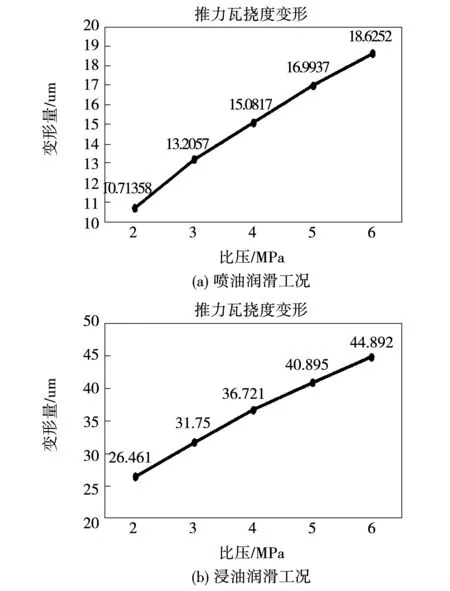
图6 两种不同工况推力瓦挠度变形Fig.6 deflect deformation of thrust tile under two different working conditions
比较喷油润滑和浸油润滑下推力瓦的热变形,喷油润滑工况的推力瓦其沿瓦厚方向的变形量比浸油润滑的推力瓦小。分析可知,在喷油润滑工况下由于瓦周边温度高,与瓦体的温差小、瓦体的温度梯度小,故瓦体凸变形小;而浸油润滑工况下油池油温恒定且较低,油池与推力瓦直接接触,两者之间温差较大,瓦体的温度梯度大,故推力瓦的凸变形也大。
4 结 论
本文以点支承可倾瓦推力轴承推力瓦为研究对象,在ANSYS DM模块中建立推力瓦的三维模型,分析并确定对推力瓦表面温度以及对流换热系数的施加方法,并在Mechanical模块中建立推力瓦有限元分析模型,对瓦的温度场进行求解计算,最终得出推力瓦的热变形分布。
结果表明,在相同结构、相同转速情况下,两种供油润滑方式的推力瓦均随比压的增大,油膜内产生的摩擦热增多,瓦表面的温度升高并使得推力瓦的变形增大;喷油润滑工况下推力瓦的挠度变形相对于浸油润滑工况下推力瓦的挠度变形偏小,但变形量均达到了与油膜厚度同一数量级。上述结论可为此类推力轴承的设计、应用提供参考依据。
