基于限速预测的一点式列车自动驾驶速度规划
2021-05-21邢键,韩冰
邢 键,韩 冰
(1.东北林业大学 信息与计算机学院,哈尔滨 150040;2.东北林业大学 机电工程学院,哈尔滨 150040)
0 引 言
铁路运输为我国运输业的主要方式之一,由于铁路网络的大规模和客货运能力,机车消耗了大量的能源,列车的自动驾驶可以避免司机因个人差异、操纵方式等原因造成的安全隐患,同时在保证列车的运营效率的前提,降低运输过程中的能耗,对于我国发展绿色交通运输方式具有重要意义。
列车节能操纵优化是一个最优化问题,以列车运行能耗为目标函数,选择合适的自变量,求解出满足相关约束条件的节能速度曲线。在对该问题的研究中,国内外的学者相继提出了不同的优化方法。
Chang等[1]采用遗传算法以列车准时性、舒适性和列车能耗为优化目标,建立了列车操纵优化模型,对列车的最优惰行控制问题进行了求解; Liang等[2]提出了一种基于罚函数法的列车运行曲线多目标优化改进的遗传算法,将罚函数法加入到适应度函数中,提高了遗传算法的收敛速度。
Frank等[3]建立了列车运行过程的非线性模型,把离散动态规划应用于列车节能最优运行曲线求解;Sager等[4]把混合整数规划方法应用于地铁列车节能优化问题,采用数值方法求解列车节能运行策略;Lu等[5]将动态规划、遗传算法和蚁群算法三种算法应用于单列车速度曲线优化,并对结果进行了比较。
Li等[6]考虑重载列车运行过程中质量的动态变化,求解使得列车准点、节能、纵向冲动尽可能小的最优操纵序列;Gu等[7]结合离线和车载优化技术,提出了一种列车节能控制框架,通过数据挖掘和机器学习建立了基于决策树的初步解决方案,车载系统将列车参数输入决策树,得到最优控制序列;Ghaviha等[8]建立了电动车组最小能耗模型,同时考虑列车运行辅助能耗,节能优化算法被成功地移植到Bombardier 公司的测试平台,为新手司乘人员提供驾驶建议指令。EffatiS等[9]采用迭代动态规划求解列车最小运行能耗问题,该方法的优点是不需要求解贝尔曼方程,能够保证结果最优性,避免了维度过大的问题。
王鹏玲等[10]根据司机优化操纵经验和典型子区间思想,将线路划分为若干区段,并提前预制停车曲线、线路限速,引入自适应机制,应用遗传算法求解列车节能最优操纵策略;李卓玥等[11]采用了粒子群算法、改进蚁群算法和粒子群-蚁群混合算法三种不同的算法设计列车节能速度曲线,并对算法的仿真结果进行了分析,取得了良好的节能效果。
冯晓云等[12]总结了优秀司机的驾驶习惯和优化操纵指导意见,设计了列车节能控制规则库,实现了基于模糊预测控制的列车自动驾驶;何庆等[13]进一步研究了司机驾驶经验和专家操纵建议,设计了模糊专家规则库,实现列车运行曲线的在线计算。唐海川等[14]将动态规划和二分法相结合,求解高速列车离线最优操纵策略,针对列车运行晚点问题,设计在线调整算法,及时重新规划列车最优运行轨迹;余进等[15]设计了两级模糊神经网络,基于离线学习的结果仿真了列车优化操纵曲线。王龙生等[16]将列车运行的安全性和车钩间的耦合力作为约束,设计了列车自动驾驶预测控制算法,通过多因素的调整,完善了列车自动驾驶控制器。徐传芳等[17]针对列车运行控制中对目标速度和位移的跟踪控制问题,建立了考虑牵引与制动转矩产生动态过程的高速列车运行模型,提出了高速列车的自适应动态面控制算法。
上述方法在列车节能操纵优化问题的求解都得到了广泛的应用,但都存在一定缺点和局限性。采用动态规划、遗传算法、蚁群算法求解最优化问题时,优化的目标较多,但是计算速度相对较慢,实时性能差[18-19]。采用极大值原理求解时,求解速度快,但是求解过程比较复杂,而且参数经简化后和实际线路存在较大的差别。
综上所述,目前存在着铁路坡道变化与限速约束等问题,求解维数大,计算过程复杂,仅能在理论层面进行简单坡道或理想坡道的仿真,很难与实际情况下的复杂情况作对比。本文基于坡道区间化简原则和区间限速规定,提出了一种化简坡道区间内仅需一种状态转换点的列车自动驾驶速度规划方案,建立了限速预测模型来提高算法效率,选择改进后的遗传算法搜索最优解,得出了列车节能操纵运行曲线,将优化的曲线与实际线路的实测数据进行对比,验证算法的可行性。
1 构建列车能耗模型
根据牛顿第二定律,单质点列车运动方程可描述为
(1)
式中:x,v,t分别为列车的位置,速度,时间变量;M,ϒ分别为列车的质量以及质量系数,通常取ϒ=0.06;f为最大牵引力;q为最大制动力;w0为基本阻力;g为坡道阻力;μf、μb分别为列车的牵引力施加系数和制动力施加系数,其中,μf∈[0,1],μb∈[0,1]。根据张小维[20]的研究结果可得列车操作工况和牵引力、制动力施加系数的关系。
运动方程的边界条件为
(2)
式中:x0,xs分别为列车运行的始末位置;v(x0)、v(xs)分别为列车运行的始末速度;v(x)、vmax(x)分别为列车在位置x处的速度及限速;T为列车的计划运行时间。
列车运行过程中的能耗主要由列车运行能耗和列车运行辅助能耗构成,列车运行辅助能耗所占总能耗比重较小,因此,本文重点讨论列车的运行能耗。
列车的运动能耗主要表现在牵引力做的功,因此列车节能优化的性能指标函数为
(3)
其中η为牵引力施加常数系数。
2 构建节能操纵模型
2.1 坡道简化
具体路段划分步骤如下:
1)合并相同类型的坡道
根据坡道大小,将符合一定规则的同类型坡道进行合并。划分标准如下:
线路总长为X,列车计划运行时间为T,定义理想巡航速度为
(4)
在当前坡度值为i的坡道上,若存在合适的μf∈[0,1]满足
μff(VX)=wo(VX)-i
(5)
则称该坡道为平缓坡,其中:μff(v)为单位牵引力;wo(v)为单位基本阻力。
若满足
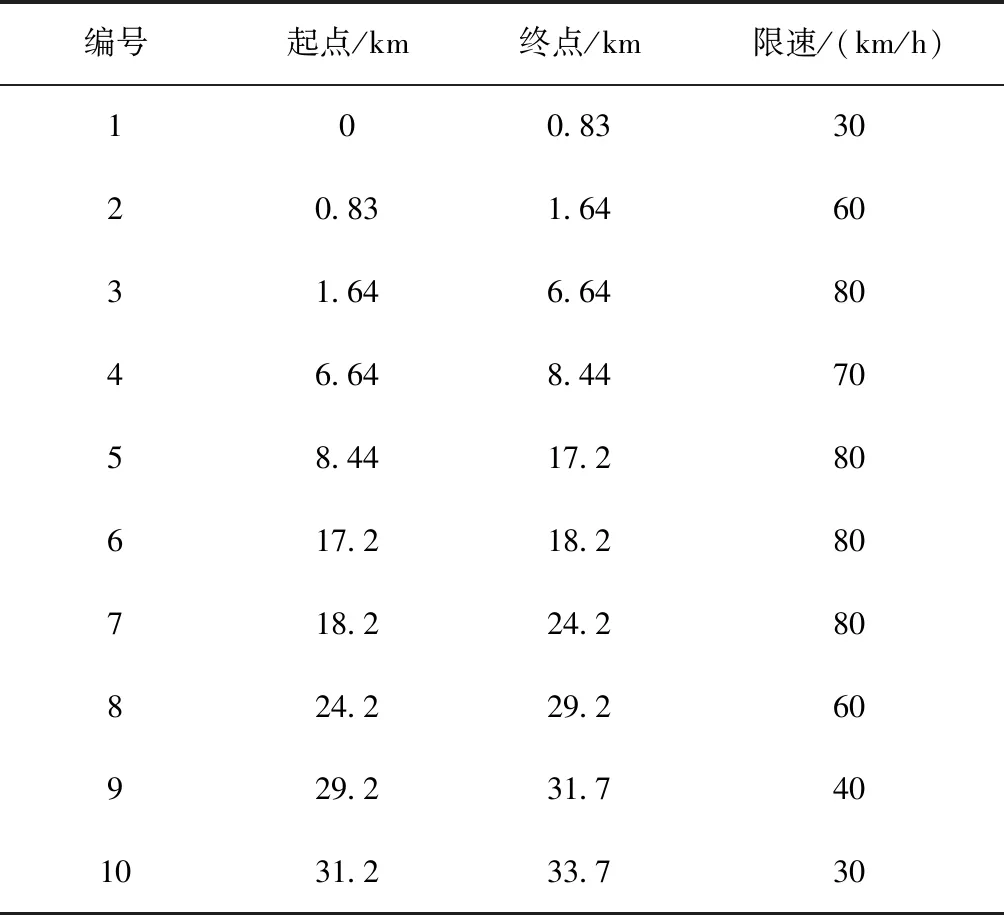
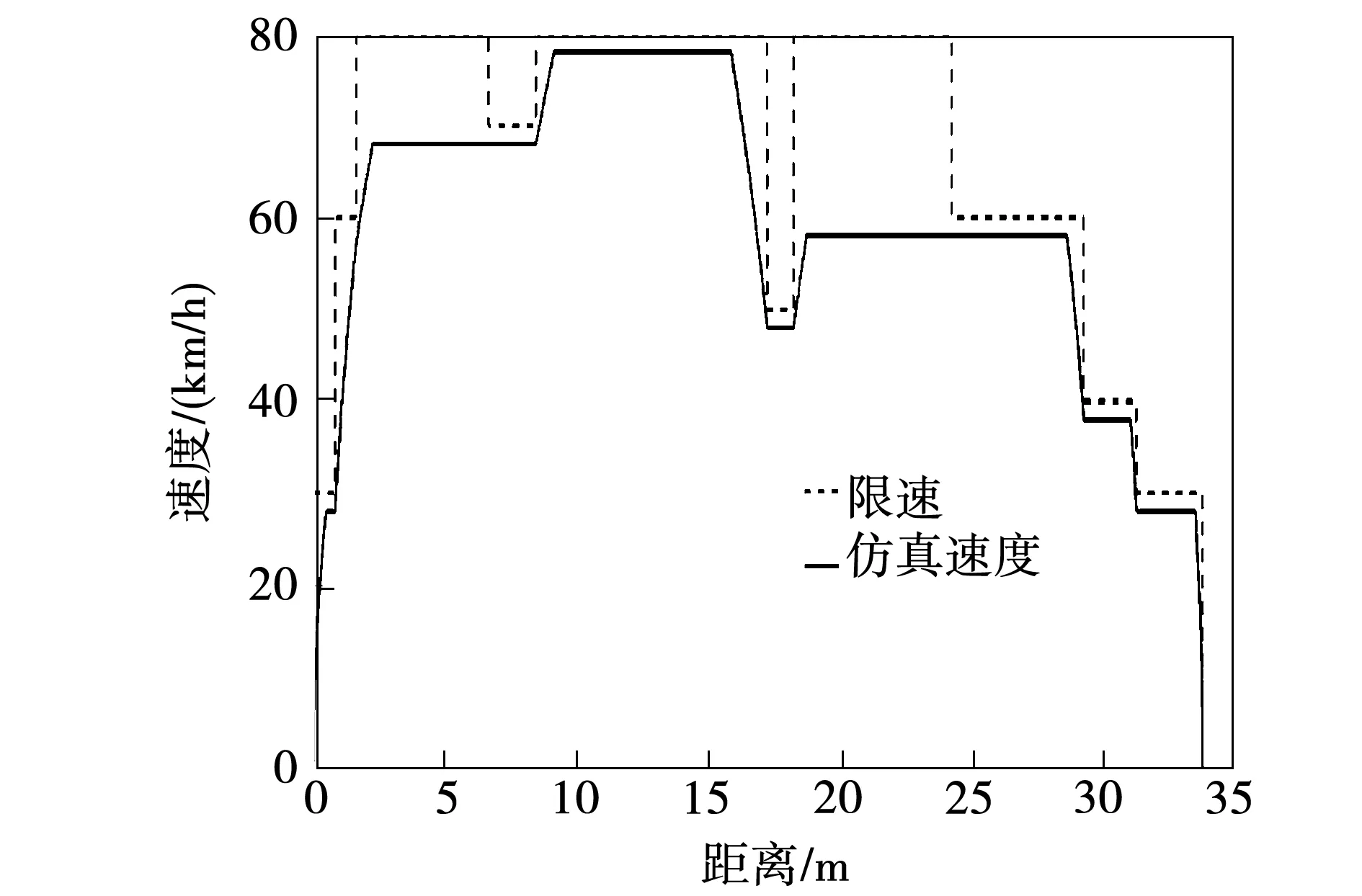
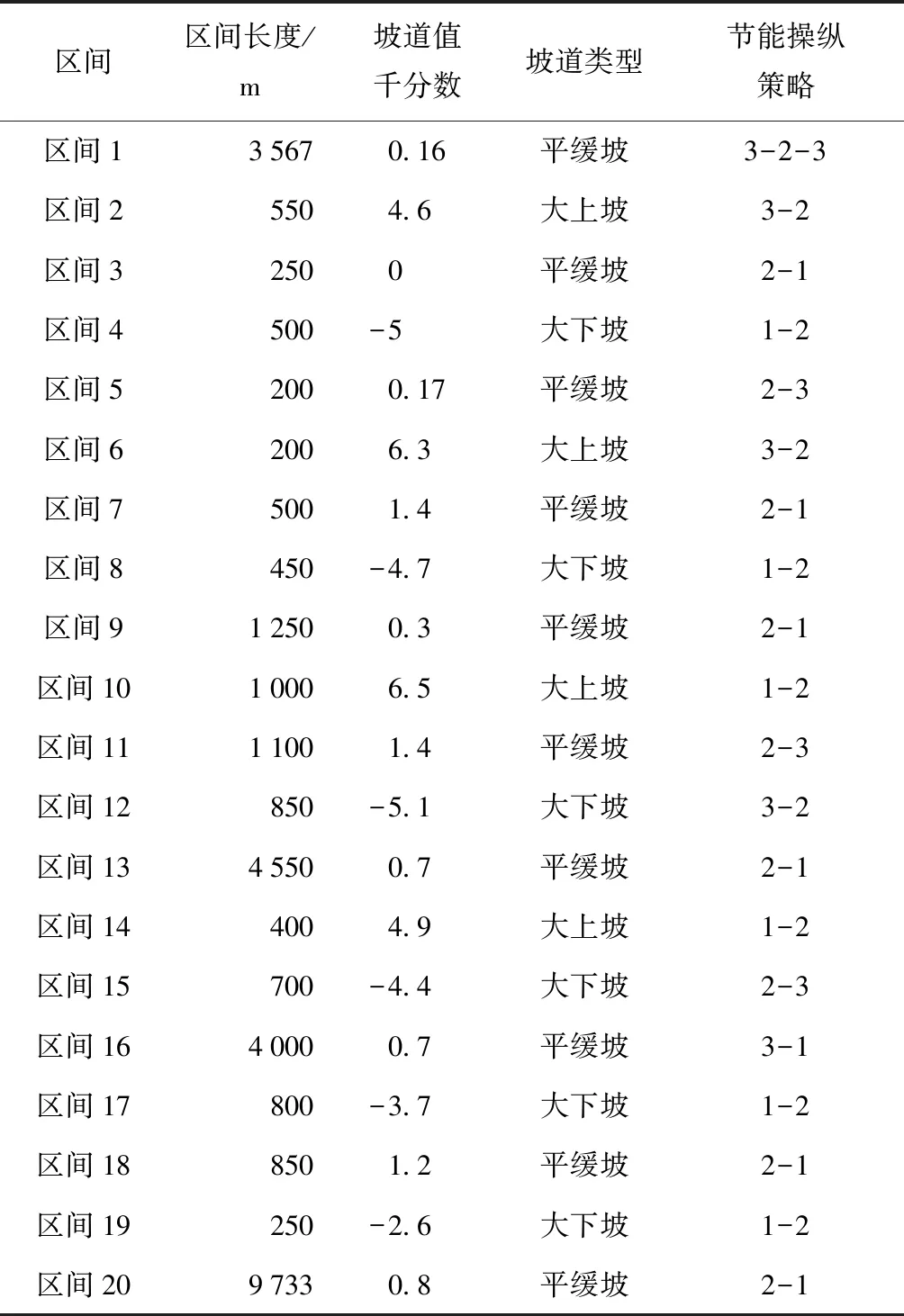
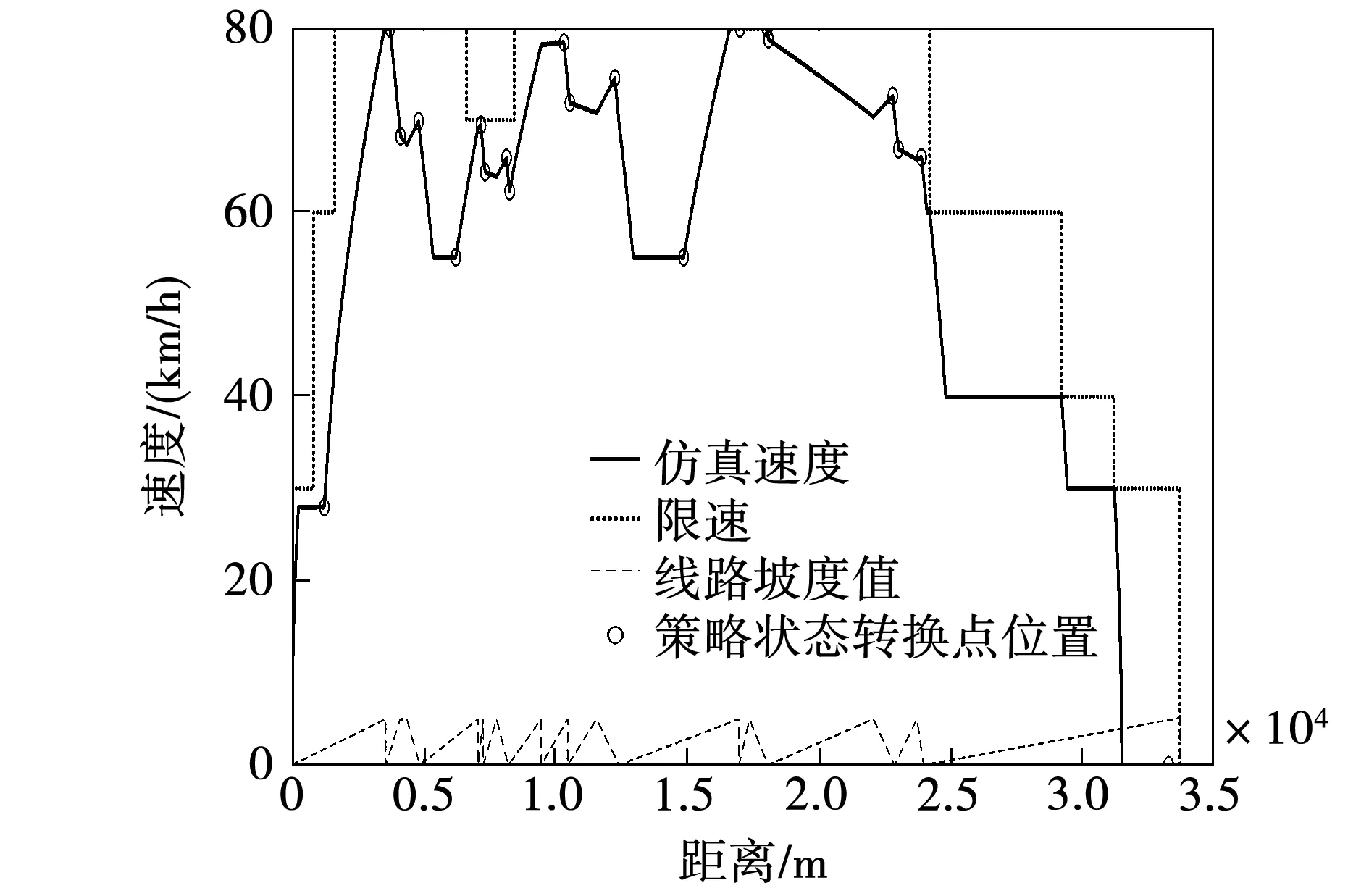
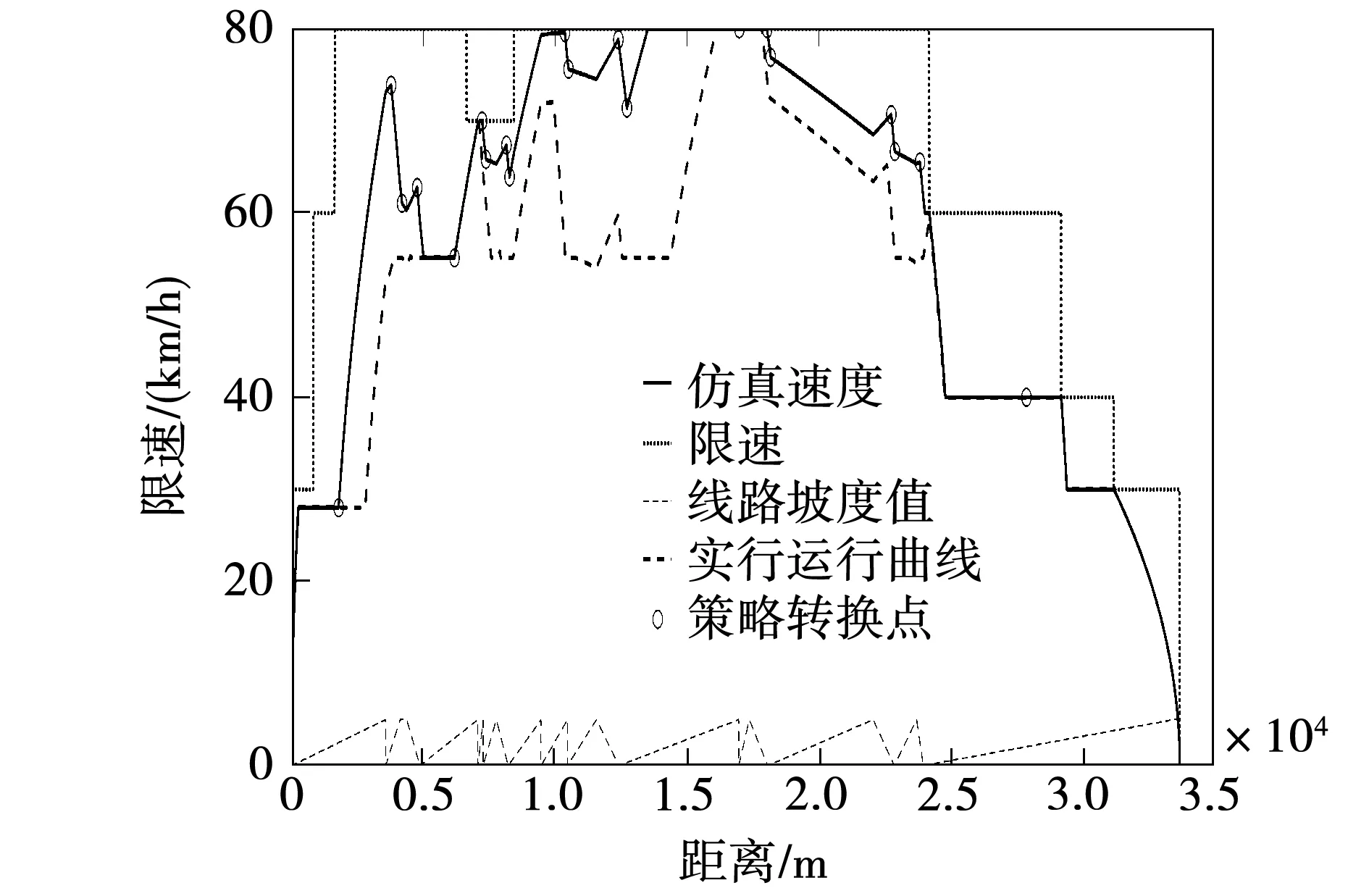
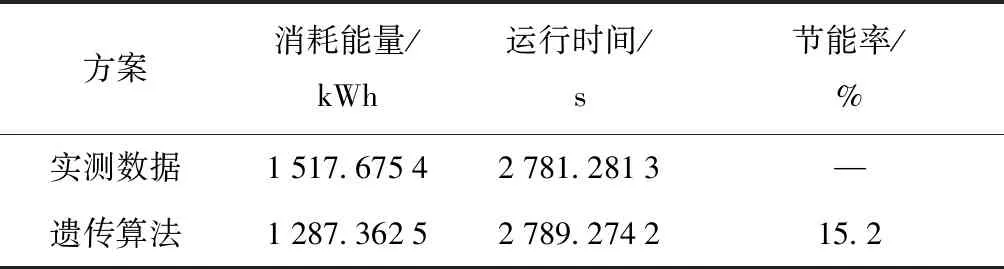
f(VX) (6) 则称该坡道为大上坡。 若满足 wo(VX) (7) 则称该坡道为大下坡。 将合并前的坡道表示为 S0=[S01,S02,…,S0i,…,S0(n-1),S0n] (8) 其中:S0i表示合并前第i个坡道的起点位置,合并前线路上共n个坡道。 按照上述坡道划分规则,可以将合并后的区间表示为 S1=[S11,S12,…,S1k,…,S1(n-1),S1n] (9) 其中:S1k表示合并后第k个区间的起点位置,合并后线路上共m个区间。 2)基于坡道一点式操纵策略区段划分 列车在运行中的操纵策略选择,不仅与当前位置所处的坡道类型有关,也与其相邻的前后两个区间的坡道类型有关。为便于描述,将列车操纵策略分为三类:全力牵引、惰行、保持巡航,分别设置各区间上的操纵策略。 ①起始过程操纵策略(3个点) 起始区间内:因起点为起始牵引点,所以将起点看作一个策略转换点,牵引阶段结束后,在第一段区间的操纵策略选择应以本区间的坡道类型和下一区间的坡道类型决定的,故在第一区段存在三个操纵策略转换点。 对于起始区间,切换点位置应满足式(10)约束: (10) 按照选取的3个策略转换点的位置,可以将起始区间按操纵策略的不同,分成3个区段。各区段对应操纵策略如表1所示。 表1 起始区间内各区段节能操纵策略Tab.1 Energy-saving operation strategy for each section in the starting interval ②运行过程操纵策略(1个点) 运行区间内操纵策略均由该区间的坡道类型和下一区间的坡道类型决定,故在运行过程区间内存在一个策略转化点。 对于第i(i≠1)个运行过程区间,切换点位置应满足式(11)约束: S1i≤Xi1≤S1(i+1) (11) 按照选取的一个策略转换点的位置,可以将运行过程区间按操纵策略的不同分成两个区段。各区段对应的操纵策略如表2、3、4所示。 当坡道为平缓坡类型时,运行过程区间内各区段对应操纵策略如下: 表2 平缓坡节能操纵策略Tab.2 Energy-saving operation strategy for gentle slope 当坡道为大上坡类型时,运行过程区间内各区段对应操纵策略如下: 表3 大上坡节能操纵策略Tab.3 Energy-saving operation strategy for large upslope 当坡道为大下坡类型时,运行过程区间内各区段对应操纵策略如下: 表4 大下坡节能操纵策略Tab.4 Energy-saving operation strategy for large downslope ③终止过程操纵策略(一个点) 终止过程区间结束时应采取制动策略,终止区间内制动前的操纵策略由该区间的坡道类型决定,故在运行过程区间内存在一个策略转化点。 对于终止过程区间,切换点位置应满足式(11)的约束。 按照选取的一个策略转换点的位置,可以将终止过程区间按操纵策略的不同,分成两个区段。由于列车运行终止需停车,为节约能量采取惰行的操纵策略,终止过程区间中各区段对应的操纵策略如表5所示。 表5 终止过程区间内各区段节能操纵策略Tab.5 Energy-saving operation strategy of each section in the termination process interval 故全路段分为m个区间,m个区间上共有m+2个转换点。相比于张小维[20]于2018年提出的线路分成m个区间上有2m+1个转换点,计算的策略转换点减少了近一倍,使算法的效率大大提高,在节能策略的选择上,本文提出的操纵策略改变的次数更少,更利于操纵。 在对列车节能操纵策略求解前,本文提出了列车限速预测辅助模型,由此确定列车在整个区段运行时的速度约束,从而避免由区段坡度决定的策略与区段限速的矛盾。 1)模型建立过程 首先,根据限速值的不同,将路段划分成不同的i段,从起点开始,逐段比较,当前限速段的限速值为Vi,与下一限速段的限速值为Vi+1。 若Vi 判断依据:利用计算机模拟列车运行,记当前第i段限速段距离为Si,计算列车加速到接近限速的加速距离为Sia,列车减速到下一段限速的减速距离为Sil。 若Si>Sia+Sil,则可以以当前限速为目标速度,否则以下一段限速为当前段的限速,依次进行迭代。 模型建立过程的流程图如图1所示。 图1 模型建立过程流程图Fig.1 Flow chart of the model building process 2)仿真算例 列车情况: 机车型号HXD3,机车重量138 t,车辆自重加载重共90 t,车辆节数40。 线路条件:如表6所示。 坡度默认为0,只考虑限速情况。 表6 线路限速情况Tab.6 Line speed limit 3)仿真结果 图2 限速预测模型仿真图Fig.2 Simulation diagram of speed limit prediction model 本文在求解状态切换点位置的方法上选择了改进后的遗传算法,对适应度函数做了改进,采用时间和能量作为联合约束,加快了收敛速度,提高了算法效率。 第i个个体代表的节能操纵方案所用的能量为Ei,第i个个体代表的节能操纵方案所用的时间为Tsi,T为计划运行时间,ΔTi为实际时间与计划运行时间的差值,则有: ΔTi=Tsi-T (12) 以时间和能量共同作为目标设计适应度函数为: (13) (14) (15) 式中:α为运行时间权重;β为列车能耗权重;φ、φ为惩罚因子。 本文仿真过程α和β取值均为0.5,即按照时间和能耗权重相同来规划列车速度曲线,φ、φ的取值均为-1 000,惩罚因子的作用为:当列车行驶速度超出路段限速,以及列车加速度变化超过规定值时,该个体的适应度值不符合实际约束,可筛选掉一部分解,提高运算效率。 在实际应用中α+β=1,α和β的取值根据计算原则而定,如更注重列车运行时间的节时运行或注重能耗的节能运行,可通过调节权重来设置。 遗传算法的算法步骤如下: 步骤1:染色体采用实数编码方式,将列车在所有区间的节能策略转换点的位置作为一个染色体,随机产生初始种群,种群数目为50; 步骤2:计算个体的适应度,并判断是否符合优化准则,若符合,输出最佳个体及其代表的最优解,并结束运算,否则转向步骤3; 步骤3:依据适应度选择再生个体,选择的方法为轮盘赌选择法;个体i被选择的概率pi为: (16) 式中:fi为个体i的适应度。 步骤4:通过交叉生成新的个体,交叉概率0.95; 步骤5:通过变异生成新的个体,变异概率0.04; 步骤6:由交叉和变异产生新一代的种群,返回步骤2; 步骤7:迭代次数为1 000次,输出最优结果。 本文在坡道化简和改进后的遗传算法的基础上,选用滨洲线的部分路段中33.7 km进行仿真运算,该线路既有较大的坡度起伏,又有相对复杂的限速条件,具有很强的代表性,可以更真实地验证遗传算法优化列车自动驾驶曲线的效果 1)列车参数 本文仿真选用的机车型号为25 t轴重的HXD3型机车,机车重量138 t,车辆为C70型号,共40节,自重取20 t,满载货物取70 t。 2)线路条件。 全段线路限速情况如表6所示。按照坡道化简规则以及上述的节能操纵策略,各区间的节能操纵策略如表7所示。其中,3代表全力牵引,2代表保持巡航,1代表惰行。 表7 区间坡道信息与操纵策略Tab.7 Interval ramp information and manipulation strategy 3)遗传算法设计 对于本文采用的路段条件,共有20个状态转换点,故染色体长度为20,种群大小为50,最大进化代数为1 000,交叉概率为0.4,变异概率为0.04,站间规定运行时间2 800 s。 仿真所用计算机处理器为Intel ®Core(TM) i5-5200U CPU @ 2.20 GHz,内存为4 GB,64位WIN10操作系统,MATLAB版本为R2018b,程序运行时间为150 s。 通过遗传算法结合限速预测模型进行不断优化,迭代次数1 000次时的速度规划曲线图分别如图3所示。 图3 遗传算法迭代1000次的列车速度规划曲线Fig.3 Speed strategy curves solved by GA with iteration 100 generation 由图3可知,遗传算法迭代1 000次时,列车运行时间为2 790 s,满足站间运行时间,同时满足站间限速规定,列车可加速至最高速度,并按照站间限速和坡道原则切换操纵策略,速度变化趋势与遗传算法设计原则相符并满足实际需求,可以很好的仿真出列车节能操纵曲线。 为进一步验证本文算法的节能效果,本文以滨洲线内某段为实验线路,实验列车由1节HXD3C型大功率机车牵引40节C70重车,线路全长33.7 km,用时47 min。 WT=W1-W0 (17) (18) 导出实验车次的列车运行过程数据记录,包括列车运行曲线、工况、减压量等。 基于上文描述的坡道化简理论和改进后的遗传算法,通过仿真得到了与实际路段相对应的运行速度曲线,如图4所示。 由图4可知,通过两种情况下列车速度曲线对比可知,在列车运行的出进站阶段,两种方案下的速度曲线变化不大,在行驶途中,遗传算法根据全局的坡道信息和限速情况,计算出满足需求的各区段状态转化点的位置,从而规划运行速度。而司机驾驶的方案中,由于个人操作水平和经验的差异,在行驶途中可能会造成更大能耗。 图4 列车自动驾驶速度规划曲线与实际曲线对比Fig.4 Comparison of train automatic driving speed planning curve and actual curve 表8 基于改进的遗传算法的仿真结果与实测数据对比Tab.8 Comparison of measured data and simulation results based on improved genetic algorithm 由表8可知,在时间方面,采用改进后的遗传算法规划得到的运行时间为2 789 s,满足规定时间;在能耗方面,采用改进后的遗传算法规划得到的能耗为1 287 kWh,相比实际运行节能15.2%。 已有方法与经典遗传算法相比,首先结合坡道化简规则,减低求解维度,提出的融合限速的操纵策略,提高了算法搜索效率。在此基础上,改进后的适应度函数在调节权重时,所需运算时间较短,避免了计算的复杂性,适用性强,同时改进后的适应度函数引入了惩罚因子,筛选掉大量不符合实际条件的解,提高了种群的成活率,也避免陷入局部最优解,更好的搜索到满足要求的解。因此,新方法在运算速率和搜索结果的有效性方面均优于经典方法。 1)本文提出了坡道化简原则,将复杂类型的坡道整合化简,降低了求解维度,建立了只需一种状态转换点的列车限速预测模型,避免由区段坡度决定的策略与区段限速的矛盾。 2)应用了对适应度函数进行改进的遗传算法,提高了种群的生存率,提升了算法运行效率和搜索的准确度。 3)通过现场实验和算法仿真结果的对比,该方法时间满足规定的运行时间,能耗与实际运行的能耗相比节约了15.2%。程序运行时间较短,为货运列车自动驾驶实际运营提供了理论基础。




2.2 融合限速的操纵策略辅助

3 基于改进遗传算法的运行策略转化点求解
4 仿真求解
5 现场实验
5.1 实验线路
5.2 数据采集
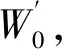
5.3 对比仿真研究
6 结 论
