双三相感应电机容错运行状态电磁力分析

2021-05-21戈宝军周晓炎陶大军

哈尔滨理工大学学报 2021年2期

戈宝军，周晓炎，陶大军，林鹏

(哈尔滨理工大学电气与电子工程学院，哈尔滨 150080)

0 引言

随着大功率电力电子技术的日益成熟，加之异步电机运行可靠，维修方便等优点，双三相异步感应电动机在越来越多的领域中得到了广泛应用[1-4]。所以无论是民用还是军用电力推进的车辆、舰艇和飞机，都要求作为动力推进用的感应电机，能够应对突发故障，即在出现故障时不能停转，允许继续容错运行一定时间[5-6]，这对电机的转矩及振动噪声提出了更高要求[7]。研究双三相感应电机电磁力对电机转矩及抑制电机振动噪声具有重要的理论和实际意义。

文[8]利用Ansoft仿真软件对多相电机不同绕线方式下的电机电磁场进行了有限元仿真，通过分析不同负载条件下的电机电磁场，研究了负载对电机噪声的影响。文[9]研究了电磁力对多相电机定子端部绕组的影响，得到运行时电机端部绕组的应力和应变分布。文[10]提出基于瞬态动力学有限元预测多相感应电机振动的方法，为优化槽配合提供参考。文[11]对大型复杂结构的多相感应电机进行电磁场分析计算，取得了气隙径向磁密结果并进行了谐波分析。文[12]研究了不同绕组结构的多相电机容错电流优化。分析发现，现有文献涉及多相电机电磁力的研究很少，有关双三相感应电动机电磁力的研究，尤其是双三相感应电机容错运行前后的电磁力研究，对电机正常运行和容错运行时的振动噪声抑制有着重要意义，相关研究有待进一步深入。

针对电磁力研究，国内外已经比较成熟，文[13]对异步电机电磁力波产生的原因在理论上进行了定性分析, 并利用解析法定量计算。文[14]基于二维瞬态有限元计算异步电机的电磁力。文[15]对三相感应电机基于计算气隙磁通密度,进而利用Maxwell应力张量法计算径向电磁力，探讨磁通密度和径向电磁力的影响,以及磁通密度波和径向电磁力波之间的关系。文[16-17]采用场路耦合有限元法，计算分析了电动机气隙磁通密度及谐波电磁力。最终给出了电磁振动的改进方向。文[18-19]通过模态分析优化结构。

为了分析容错前后和故障运行时的电磁力对双三相感应电机振动和噪声的影响，并同时考虑磁路的饱和，本文将结合时步有限元磁场分析和麦克斯韦张量法，计算双三相感应电机在额定、缺相、容错时的切向电磁力密度及径向电磁力密度，并进行频谱分析，对比和总结变化规律。同时，通过对比电磁转矩的有限元分析结果，验证电磁力密度计算方法的准确性，并对整台双三相感应电机进行电机固有频率分析，从而验证电机针对振动噪声的合理性。

1 双三相感应电机的物理模型与电磁力密度算法

表1给出了双三相感应电机主要参数，图1为其物理模型。

表1 双三相感应电机主要参数Tab.1 Main parameters of double three-phase induction motor

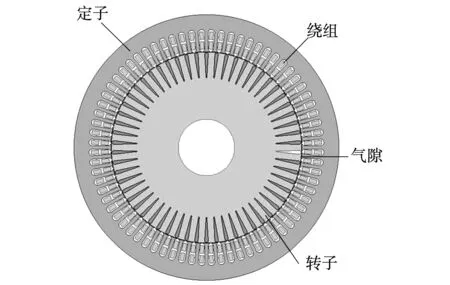
图1 双三相感应电动机物理模型Fig.1 Physical model of double three-phase induction motor

在双三相感应电机二维全域模型内，电机瞬态电磁场微分方程可用矢量磁位表示为

(1)

式中：Az和Jz为矢量磁位和电密的轴向分量；μ为磁导率；σ为电导率；L1为定子铁心外圆边界。

双三相感应电动机转子表面与定子内表面之间存在气隙，气隙中空气相对磁导率为1。其由麦克斯韦张量法得到的径向与切向电磁力密度可按气隙磁场的电磁力密度进行计算[20]：(本文中电磁力密度计算选取代表位置为：定子齿顶。)

(2)

式中：pn与pt分别为径向与切向电磁力密度；Bn为径向气隙磁密；Bt为切向气隙磁密。

2 电机容错前后的电磁力密度分析

2.1 电机磁场分布的有限元分析

双三相感应电动机额定稳态、缺相时、容错稳态时磁场分布图如图2所示，电机正常运行时，磁场分布均匀；发生缺相后，局部磁力线分布不均匀，定子齿部、轭部磁密下降；容错后电机磁场分布均匀，与电机正常运行时相比变化不大。

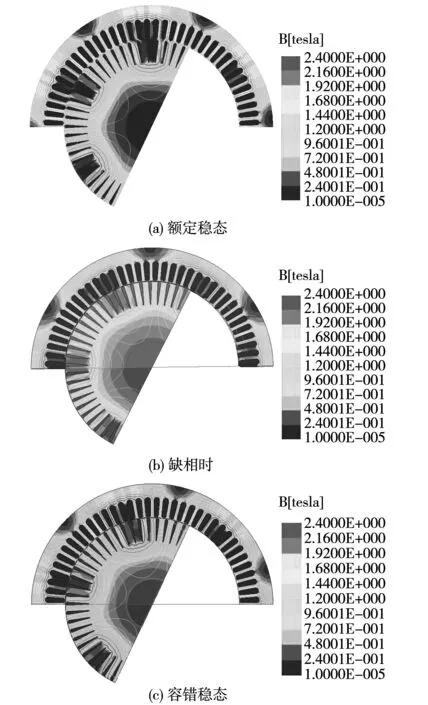
图2 磁场分布图Fig.2 Magnetic field distribution curve

2.2 电机径向电磁力密度分析

根据电机气隙磁场分布的计算结果，根据式(2)，求得双三相感应电动机在额定稳态、缺相时、容错稳态的径向电磁力密度空间波形如图3所示。

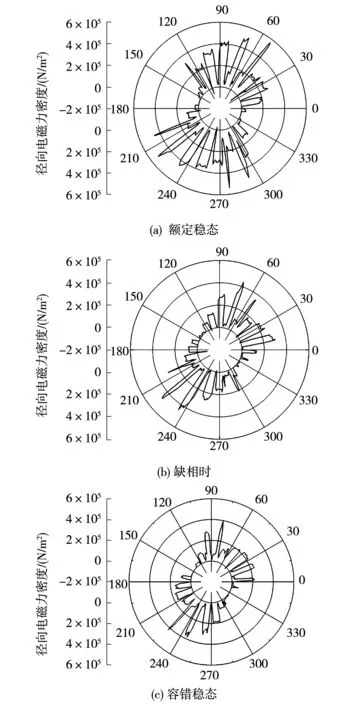
图3 径向电磁力密度图Fig.3 Radial electromagnetic force density

由图3可见，双三相异步感应电动机径向电磁力密度在一个机械周期内呈对称分布，其周期变化次数与电机极数相同。同时，由于齿槽效应，与定子齿部相对径向电磁力密度，大于与槽口相对的径向电磁力密度。此外，额定稳态时径向电磁力密度峰值为5.67×105N/m2，而缺相时为4.72×105N/m2，相比降低16.7%，容错后稳态时径向电磁力密度峰值为4.23×105N/m2，比缺相时降低10.4%，比额定稳态时降低25.4%。额定稳态到缺相状态时，电机的径向电磁力密度呈下降趋势；缺相状态到容错后稳态时，电机的径向电磁力密度也呈下降趋势。

2.3 电机径向电磁力密度频谱分析

对关于时间分布的径向电磁力密度进行频谱分析，得到径向电磁力密度的频谱图如图 4所示。

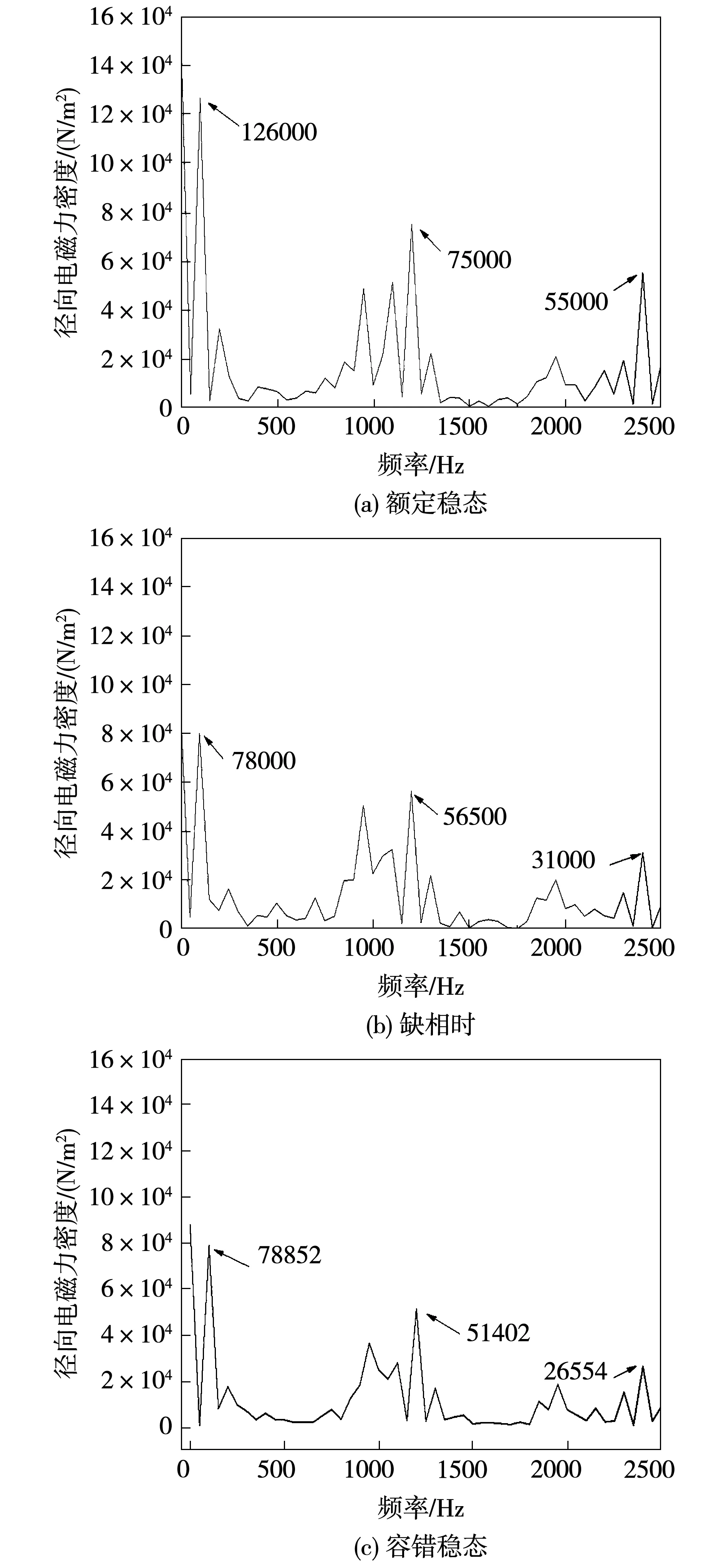
图4 径向电磁力密度频谱图Fig.4 Radial electromagnetic force density spectrogram

从图 4可见，额定稳态时2倍频产生的径向电磁力密度峰值为1.26×105N/m2，缺相时为7.8×104N/m2，相比降低38.1%，容错后稳态时切向电磁力密度峰值为7.885 2×104N/m2，比缺相时下降1.1%，比额定稳态时下降37.4%。额定稳态时12倍频产生的径向电磁力密度峰值为7.5×104N/m2，缺相时为5.65×104N/m2，相比降低24.6%，容错后稳态时切向电磁力密度峰值为5.140 2×104N/m2，和缺相时下降9%，比额定稳态时下降31.5%。额定稳态时24倍频产生的径向电磁力密度峰值为5.5×104N/m2，缺相时为3.1×104N/m2，相比降低43.6%，容错后稳态时切向电磁力密度峰值为2.655 4×104N/m2，比缺相时下降14.3%，比额定稳态时下降52%。额定稳态到缺相状态时，电机的切向电磁力密度大幅下降；缺相状态到容错后稳态时，电机的切向电磁力密度呈下降趋势。

2.4 电机切向电磁力密度分析

根据电机气隙磁场分布的计算结果，根据式(2)，求得双三相异步感应电动机在额定稳态、缺相时、容错稳态的切向电磁力密度波形时间波形，如图5所示。

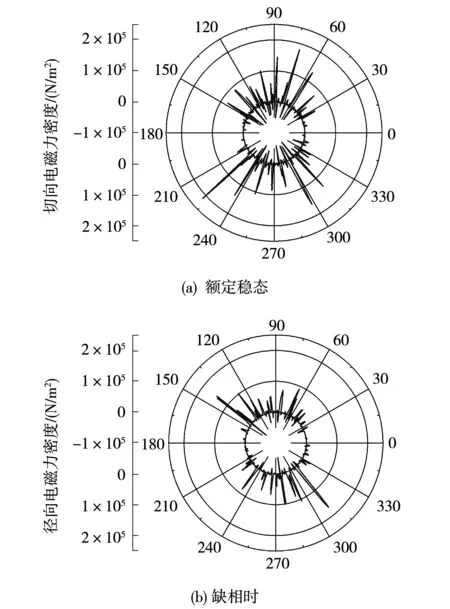
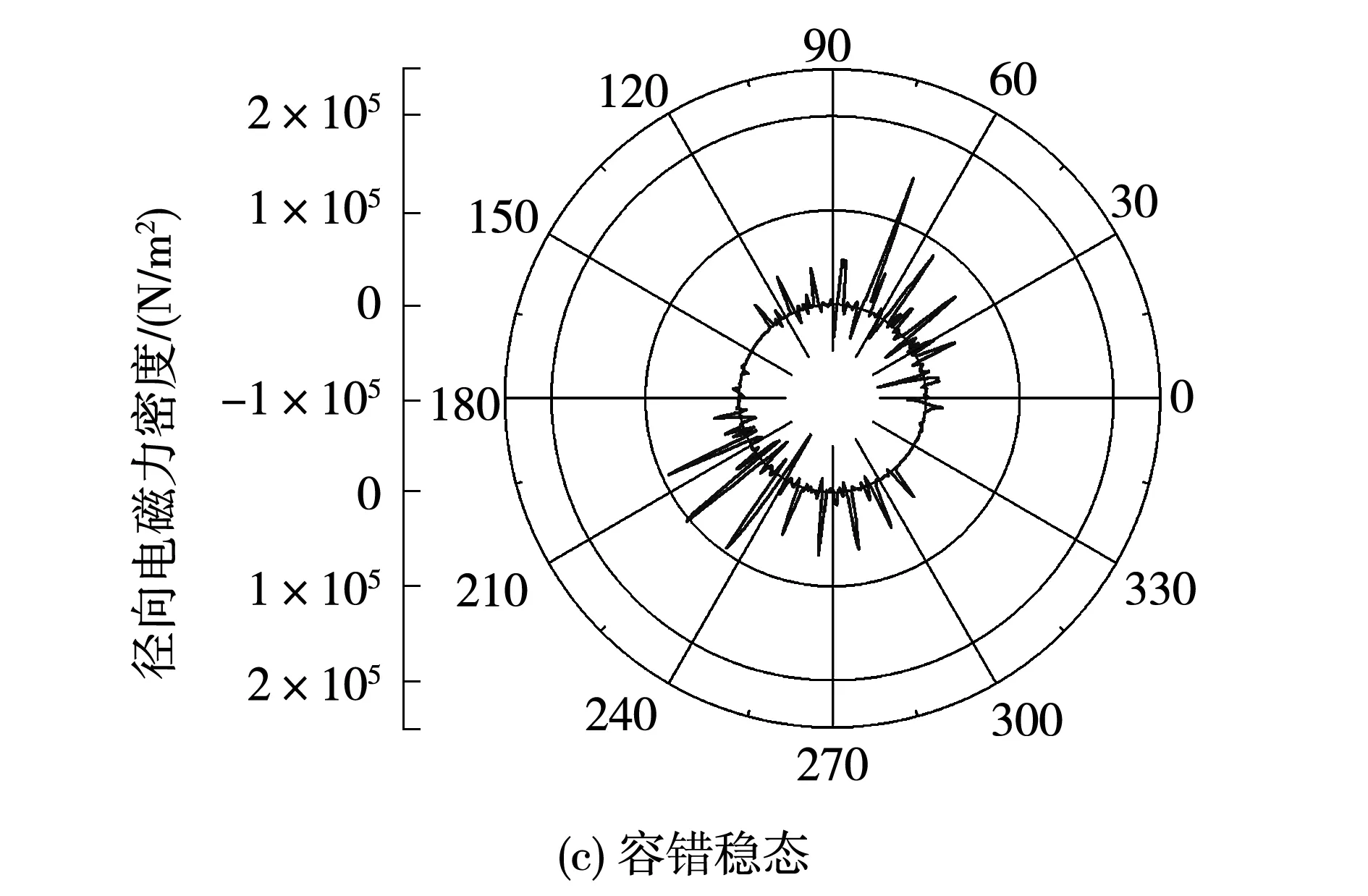
图5 切向电磁力密度图Fig.5 Tangential electromagnetic force density

由图5可见，双三相异步感应电动机切向电磁力密度在一个机械周期内呈对称分布，其周期变化次数与电机极数相同，此外，额定稳态时切向电磁力密度峰值为2.14×105N/m2，缺相时为1.53×105N/m2，相比降低28.5%，容错后稳态时切向电磁力密度峰值为1.49×105N/m2，比缺相时降低2.6%，比额定稳态时降低30.2%。额定稳态到缺相状态时，电机的切向电磁力密度大幅下降；缺相状态到容错后稳态时，电机的切向电磁力密度呈下降趋势。

2.5 电机电磁转矩分析

电机切向电磁力主要产生切向电磁转矩[18-20]，双三相电机额定稳态时、缺相时、容错稳态时的电磁转矩，如图6所示。

图6分别显示了最后0.02 s时间(一个周期)的转矩波形，额定运行时电机经过约1.22 s的时间后，转矩响应趋于稳定，可以看到额定稳态时电机额定转矩为1 125 N·m；缺A相时的双三相感应电动机的额定转矩为1 018 N·m，相比降低9.5%，且电机转矩波动明显增大，处于914～1 116 N·m之间；容错电机经过2.82 s的时间后，转矩响应趋于稳定，容错后的双三相感应电动机的额定转矩为621 N·m，相比额定稳态时转矩降低44.8%；和缺相时相比转矩增加39%，且转矩波动明显要小。额定状态到缺相时电机平均转矩呈下降趋势，缺相时到容错稳态后电机平均转矩呈大幅下降趋势，容错稳态后平均转矩相比于额定稳态时电机平均转矩呈大幅下降趋势。

双三相感应电动机额定稳态时、缺相时、容错稳态时对转矩波形进行傅里叶分解得到的电磁转矩谐波分析，如图7所示。

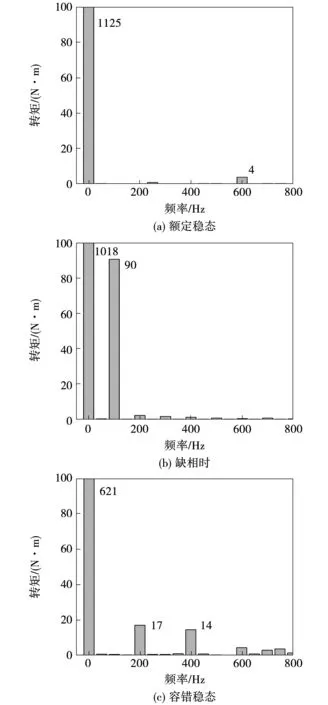
图7 电磁转矩谐波分析Fig.7 Harmonic analysis of electromagnetic torque

由图7可见，三相感应电机额定稳态运行时消除了5、7次谐波磁势，总的6次谐波转矩为零，转矩脉动的最低次数提高到12次，幅值为4 N·m；缺相时系统中存在较大的2次谐波转矩，幅值为90 N·m；容错稳态后双三相感应电机存在幅值为17 N·m的4次谐波及14 N·m 的8次谐波。

3 电磁转矩计算的合理性验证

切向电磁力主要产生切向电磁转矩，具体为：

(3)

式中Lef为电机有效长度。

采用电磁力计算结果比对验证双三相电机容错运行稳定后的电磁转矩，如图8所示。样机试验后的电机电磁转矩结果见表2。

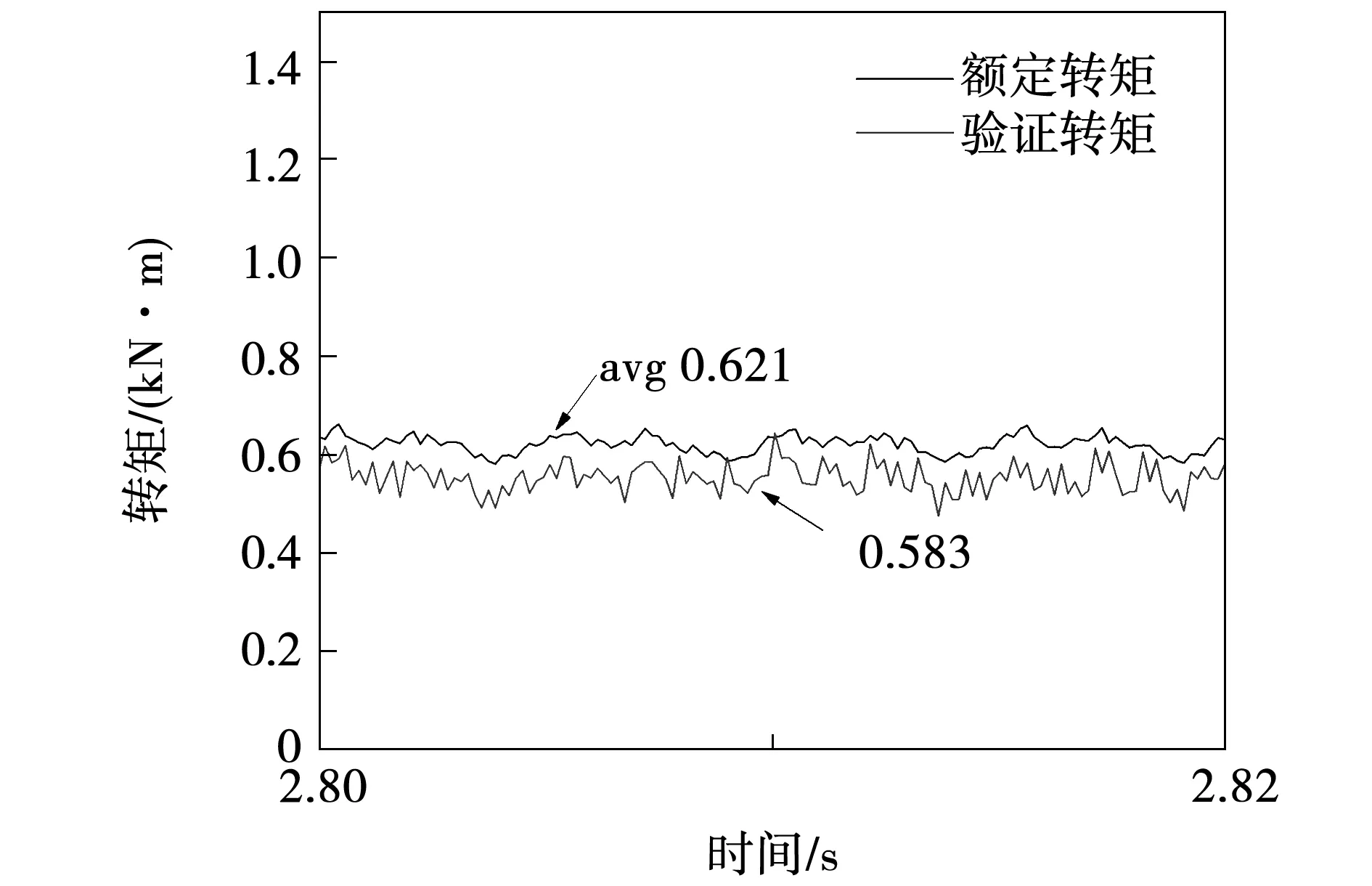
图8 电磁转矩Fig.8 Electromagnetic torque

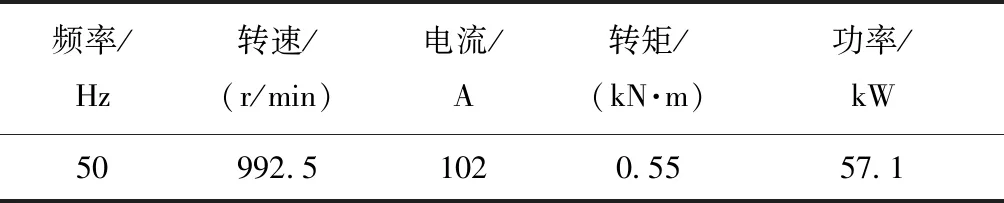
表2 双三相感应电机试验电磁转矩结果Tab.2 The load characteristics of the cast copper rotor motor

从图8及表2可知，双三相电机容错运行稳定后的平均电磁转矩为0.621 kN·m，电磁力计算的平均电磁转矩为0.583 kN·m，样机试验后的电磁转矩为0.55 kN·m。电磁力计算的转矩要小于双三相电机容错运行稳定后的电磁转矩，电磁转矩稳定后平均值相差6.1%。试验后的电磁转矩要小于双三相电机容错运行稳定后的电磁转矩，电磁转矩稳定后数值相差11.4%，与验证电磁力计算转矩相差5.6%，结果基本一致，从而验证了本文电磁转矩计算结果的准确性。

4 电机验证合理性分析

采用简化后的双三相感应电机的整机模型进行振动模态和固有频率计算，同时设定端盖与机座通过紧密接触的设定来模拟过渡配合，计算双三相感应电机的各阶振动模态，其二至三阶模态振型的分析结果如图9所示。

图9 双三相感应电机模态振型Fig.9 Modal shape of double three-phase induction motor

由图9可见，当电机的固有频率随着电机振动模态的阶数增加时，电机整体变形量增大。对电机振动噪声起主要作用的铁心变形量降低，即二阶模态时电机铁心变形最为严重，也对电机的振动噪声影响最大。为验证双三相感应电机针对振动噪声设计的合理性，双三相电机三维模型的前三阶固有频率与径向电磁力密度频谱对比如图10所示。

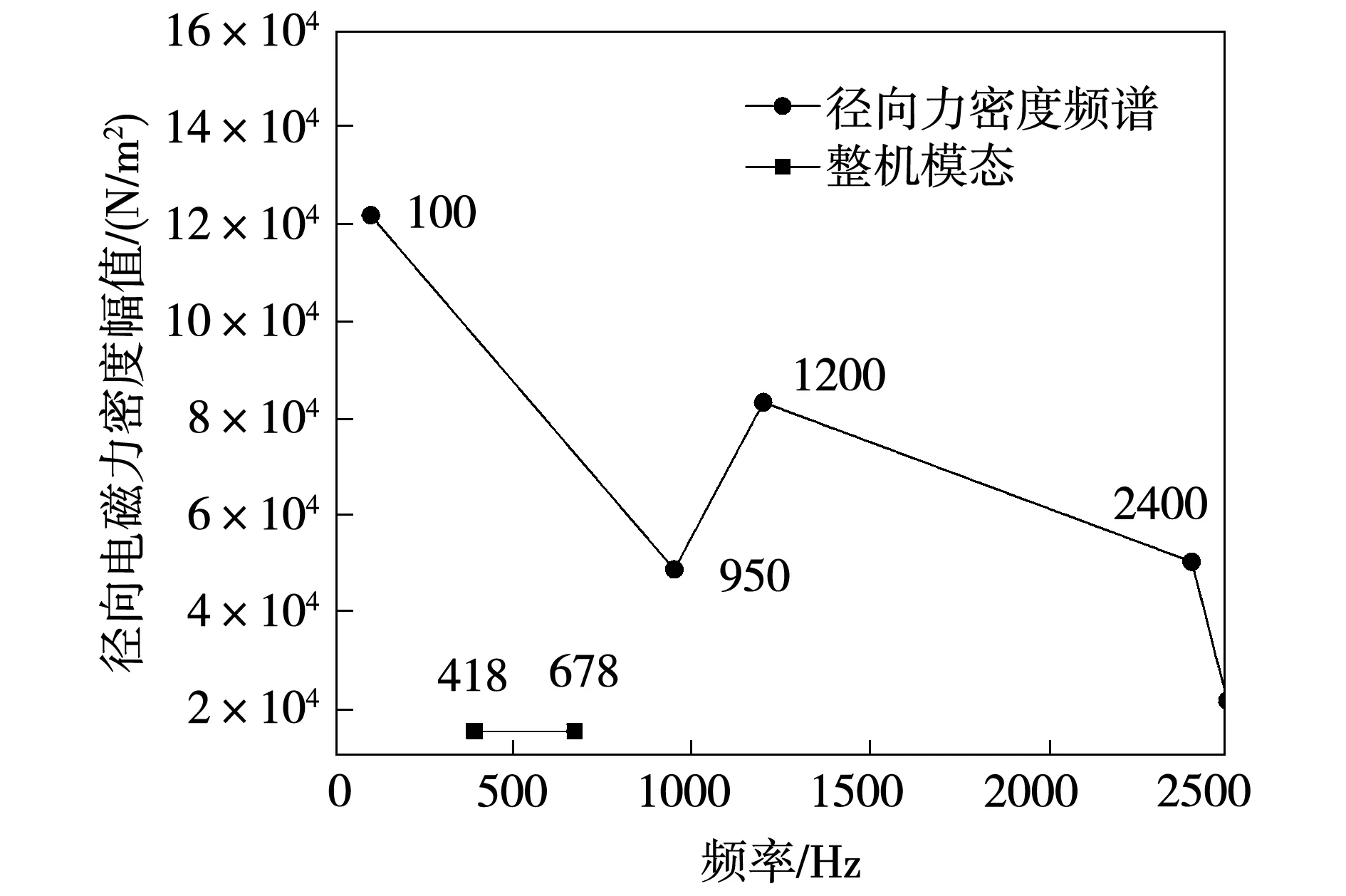
图10 固有频率与径向电磁力密度频谱对比Fig.10 Natural frequency versus radial electromagnetic force density spectrogram

由图10可见，对电机振动噪声起主要作用的二阶模态振型的电机固有频率为418 Hz，三阶模态振型的电机固有频率为678 Hz。与径向电磁力密度的频谱相比较可得出，本文研究的双三相异步感应电动机固有频率与径向力密度频谱中产生峰值时的频率点不重合，双三相感应电机将产生较小的振动与噪声。

为证明双三相感应电机将产生较小的振动与噪声，对样机进行试验如图11所示。得到双三相感应电机的振动值为0.6 mm/s，小于国家标准GB10068《轴中心高为56 mm及以上电机的机械振动振动的测量、评定及限值》中：表1等级A中的刚性安装时振动标准值2.3/mm/s。噪声值为72.48 dB，小于国家标准GB10069.3《旋转电机噪声测定方法及限值第3部分：噪声限值》中表1标准值98 dB。