游客量预测对客运量的影响量化研究

宋 洁，张文华

（苏交科集团(甘肃)交通规划设计有限公司，兰州730030）

一、引言

随着国民经济的发展和人民生活水平的提高，人们对精神文化的需求进一步提升，文化旅游逐渐成为一种幸福、快乐、健康、美好的生活方式。文化旅游满足了新时期人们对美好生活和精神文化的需求。甘肃是丝绸之路的黄金路段，长达一千六百余公里的景观长廊串起了河西四郡、嘉峪雄关、金城古渡、麦积烟云等。沿着今日的丝绸之路，甘肃走廊已经成为一条名胜荟萃、古迹璀璨、风光壮美、风情浓郁的旅游景观长廊。预测景区游客人数，合理规划旅游交通及景区设施，顺应时代发展，实现交通与旅游融合发展。

1967 年，Cover 和Hart 提出KNN 算法（k-Nearest Neighbor），该算法是一种经典的模式识别方法，常用于分类。KNN 回归算法则可用于预测，具有简单易实现、计算效率高、实时性好等特点。陆利军等提出利用EMD-BP 算法预测游客量，EMD 提升了BP神经网络算法的预测精确度。陈涛等分别利用VAR模型和BP 神经网络模型预测游客量，研究表明，BP神经网络模型的预测精确度和稳定性优于VAR 模型。张泽汉等指出，由于近年来游客量的变化呈线性变化趋势，故使用二次指数平滑预测游客量。郭鹏提出GM（1，1）模型群分段选优预测游客量，预测精确度均高于99%。曾东玲等提出，利用灰色模型预测云南旅游市场，并利用马尔科夫进行修正，达到了预期效果。王琳提出利用Elman 神经网络的入境游客量预测模型。研究表明，Elman 神经网络的预测误差较小，预测结果与实际接近。张英坤等提出将灰色系统GM与RBF 神经网络相融合，预测混凝土碳化深度。研究表明，融合模型的预测精确度高于GM和RBF 神经网络的预测精确度。文献利用粒子群优化神经网络，研究表明，优化后提高了模型的预测精确度，该融合模型具有较强的实用性和抗噪性。YU H H 等提出利用粒子群优化LSSVM，研究表明，粒子群算法提高了LSSVM 算法的预测精确度。张莹莹提出利用ARIMA 模型预测中国猪肉价格，预测效果较好。机器学习应用中，比较常用的时间序列预测方法有自回归平均移动模型（ARIMA）、灰色系统预测模型（GM）和神经网络模型等，其中ARIMA 模型多用于线性时序数据预测，GM模型多用于时间序列数量较少的时间序列，BP 神经网络适用于非线性时序数据预测，Elman 神经网络与BP神经网络类似，算法都是采用基于梯度下降法，会出现训练速度慢和容易陷入局部极小点的缺点，对神经网络的训练较难达到全局最优。

总结国内外相关研究可以得出，关于时间序列的预测方法是比较多的，但是没有充分考虑时间序列数据的特点，故预测效果没有达到最佳。现结合样本数据的特点，提出基于ARIMA 模型和RBF 神经网络模型的预测方法。

二、理论基础

每种预测模型都有其各自的优势，ARIMA 模型适用于预测线性部分，而RBF 神经网络模型适用于预测分析线性部分，RBF 神经网络具有全局逼近能力，解决了BP 网络的局部最优问题。ARIMA 模型与RBF 神经网络模型可以相互补偿，从而使得预测结果更佳精确。

（一）自回归差分移动平均模型（ARIMA）

1.ARIMA 原理。ARIMA 模型是由博克思（Box）和詹金斯（Jenkins）于70 年代初提出的一种时间序列预测方法。该模型的基本思想是将预测对象随时间推移而形成的数据序列作为一个随机序列，利用数学模型来近似描述该随机序列，数学模型被识别后就可以从时间序列的过去值和现在值来预测未来值，ARIMA 模型的数学表达式如式（1）所示。

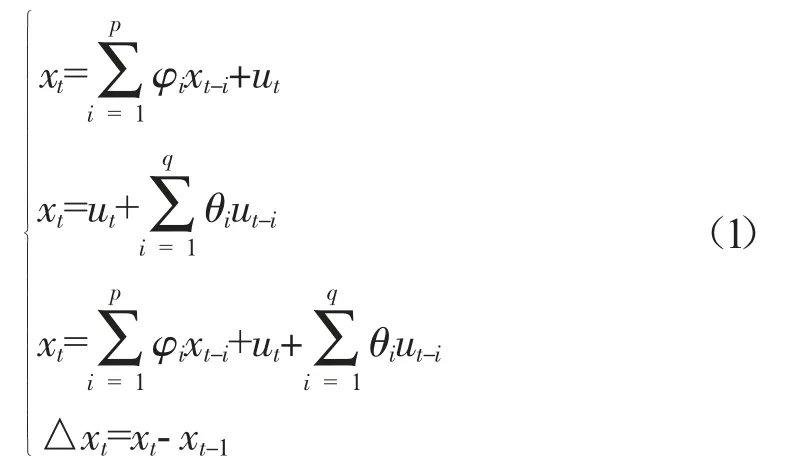
2.ARIMA 建模流程。一是平稳序列（差分法确定d）；二是确定p 和q 阶数，ACF 与PACF；三是建立ARIMA（p、d、q）。

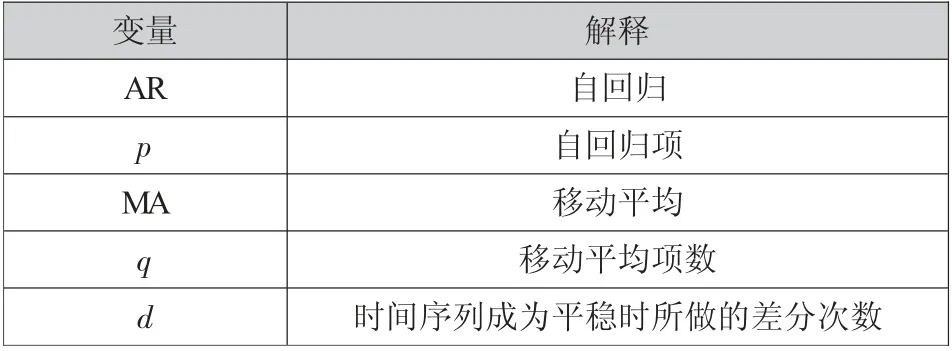
表1 变量及解释Tab.1 variables and interpretation

（二）RBF 神经网络

1.RBF 神经网络原理。RBF 神经网络是一种性能优良的前馈型神经网络，其三层结构，包括输入层、隐含层和输出层。该算法的特点是从输入层到隐含层的变换是非线性的，而从隐含层到输出层的变换是线性的。RBF 能够实现无限逼近，RBF 神经网络的逼近精度要明显高于BP 神经网络，RBF 神经网络原理示意图如图1 所示。图1 中，‖dist‖表示求取输入向量和权值向量的距离，神经元（radbas）的输入为输入向量p 和权值向量w 的距离乘以阈值b，高斯函数（radbas）是常用的径向基函数，其表达式为f(x)=e-x2。

图1 RBF 神经网络原理示意图

2.交叉验证。交叉验证法通常用于机器学习建立模型和验证模型的参数，其基本思想是将样本数据集分为两部分，一部分为训练集，另一部分为验证集，经过反复训练模型的超参数，最终得到预测模型的最优参数。常用的交叉验证法有简单交叉验证法、S 折交叉验证法和留一交叉验证法，现采用S折交叉验证法，该算法原理如图2 所示。

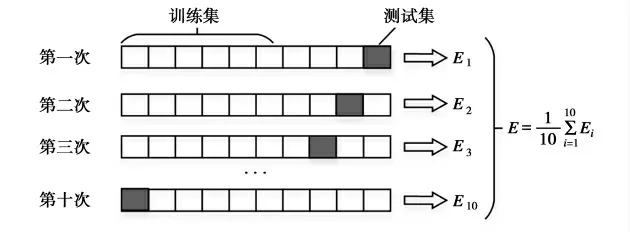
图2 S 折交叉验证法原理示意图

（三）误差分析理论

误差用于度量实际值与预测值之间的差距，通过误差分析衡量预测模型的预测性能。常用的误差分析方法有平均绝对误差（MAE）和均方根误差（RMSE），其数学表达式如式（2）和式（3）所示。

其中，ot表示观测值，pt表示预测值。

（四）回归分析原理

回归分析方法的基本思想是基于自变量和因变量的一组观测数据，找一个函数式，通过这个函数式将自变量和因变量之间的统计相关关系近似地表达出来。函数式的一般表达式如式（4）所示。

其中，y、xm为观测值，βm为回归系数，ε 为误差。

三、实证分析

（一）描述性分析

随着我国社会经济的发展，人们生活水平不断提高，人们对于精神需求更加注重，旅游成为满足人们精神需求的最佳选择，2000-2019 年甘肃省国内旅游接待人数的变动特征如图3 所示。

图3 2000-2019 年甘肃省国内旅游人数变动特征

由图3 可知，2000-2019 年甘肃省国内旅游接待人数呈指数型增长，2000-2008 年甘肃省国内旅游接待人数平稳增长，随着国民经济的增长，2009-2019 年甘肃省国内旅游接待人数迅速增长。

（二）预测分析

1.ARIMA 预测。利用SPSS 软件反复测试，确定ARIMA 模型的参数p、d 和q，最终建立ARIMA（1，2，1）模型，预测甘肃省国内旅游接待人数，预测结果如图4 所示。由图4 可知，整体而言，ARIMA 模型的预测效果是比较好的。2008 年预测值的偏差较大，其他时间节点的预测值与实际值比较接近。

图4 ARIMA 预测效果图

2.RBF 神经网络预测。由于样本数据量有限，故采用交叉验证的方法，训练模型的超参数，最终得到最优参数。利用MATLAB软件建立反复训练模型，得到最佳网络参数，然后预测甘肃省国内旅游接待人数，最终得到的预测效果图如图5 所示。由图5可知，2002-2008 年的预测误差比较大，2009-2019年的预测误差较小。结果表明，RBF 神经网络模型并不适用于线性部分的预测，对于线性部分的预测误差较大。

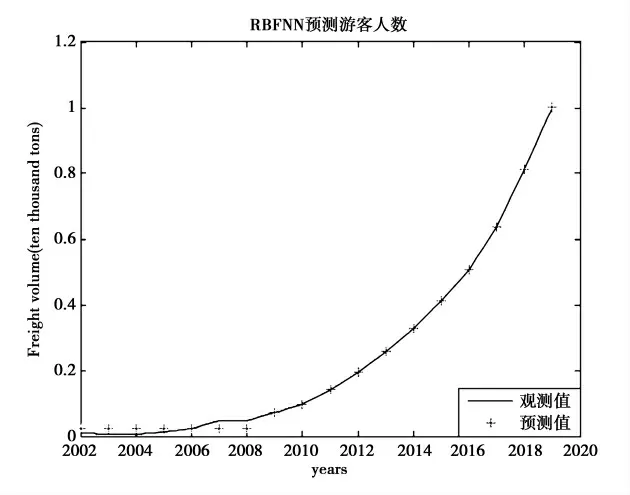
图5 RBF 神经网络预测效果图

3.ARIMA-RBFNN 预测。利用残差优化法将ARIMA 模型和RBF 神经网络模型融合，预测甘肃省国内游客接待人数，ARIMA-RBFNN 的预测效果图如图6 所示。由图6 可知，ARIMA-RBFNN 融合模型的预测效果是比较好的，预测值与实际值比较接近，该融合模型的预测误差较小。

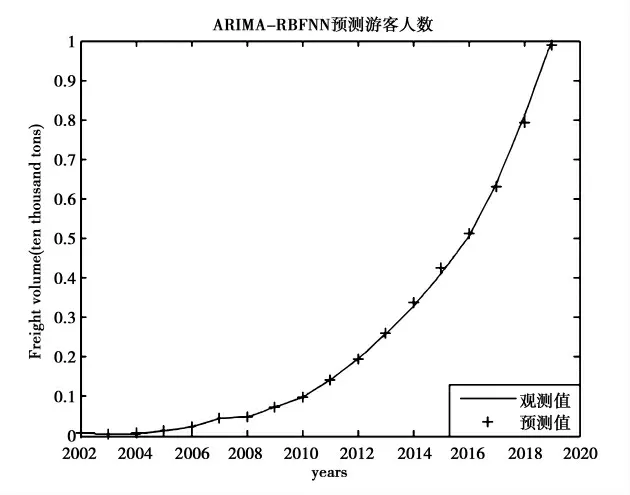
图6 ARIMA-RBFNN 预测效果图

（三）误差分析

利用误差指标（MAE 和RMSE）评价预测模型的预测性能，ARIMA 模型、RBF 神经网络模型和ARIMA-RBFNN 模型的预测误差分析结果如表2所示。

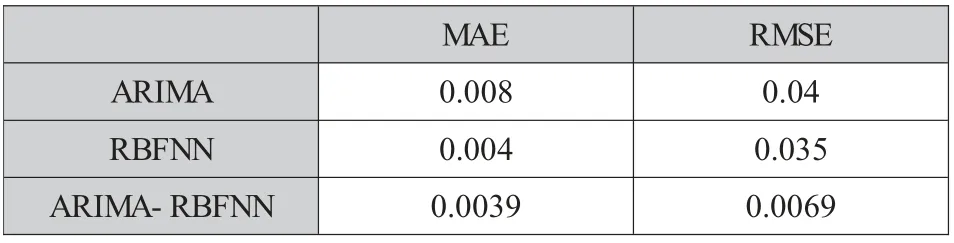
表2 误差分析表Tab.2 error analysis table

由表2 可知，相比较而言，ARIMA-RBFNN 模型的预测性能最好，预测误差最小。ARIMA-RBFNN模型的预测误差指标MAE 和RMSE 分别为0.0039和0.0069。可以得出，ARIMA-RBFNN 融合模型改善了ARIMA 模型和RBFNN 模型的预测性能，使得预测结果更接近实际值。

四、游客量与交通客运量的关系

旅游业与交通存在着密切关系，交通便利会带动旅游业的发展，与此同时，旅游业增加了交通运输量。利用多元回归分析游客量与各种运输方式之间的数量关系，结果如式（5）所示。

其中，y 表示国内游客接待人数；x1表示铁路客运量；x2表示公路客运量；x3表示民航客运量。

由公式（5）可以得出，甘肃省国内游客接待人数与铁路客运量、公路客运量以及民航客运量之间的数量关系分别为7.44、-0.09 和0.76。

五、结论

一是利用残差优化法，将ARIMA 和RBF 神经网络融合，预测甘肃省国内游客接待人数。研究表明，融合算法改善了ARIMA 和RBF 神经网络的预测性能，从而提高了预测精确度。二是RBF 神经网络的预测精确度高于ARIMA 的预测精确度，且RBF 适用于非线性部分的预测。三是利用多元回归分析可得，游客量与铁路客运量、公路客运量以及民航客运量存在一定的数量关系。