预制T梁单梁静载试验结果的不确定度分析研究

陈耀辉

(1.河北瑞志交通技术咨询有限公司 石家庄市 050091； 2.河北省道路结构与材料工程技术研究中心 石家庄市 050091)

0 引言

“根据所用到的信息，表征赋予被测量值分散性的非负参数。”是JJF 1059.1—2012《测量不确定度评定与表示》中，给出的测量不确定度(或简称不确定度)的定义[1]。测量不确定度包括由系统影响引起的分量，如遇修正量和测量标准所附量值有关的分量及定义的不确定度。测量不确定度一般有若干分量组成，其中一些分量可根据一系列测量值的统计分布，按测量不确定度的A类评定进行评定。而另一些分量则可根据基于经验或其他信息获得的概率密度函数，按测量不确定度的B类评定进行评定，A、B类不确定度均可用标准偏差表征[2]。测量不确定度越小，测量结果的水平越高，测得量值的使用价值越高；测量不确定度越大，测量结果的水平越低，测得量值的使用价值越低。

利用静载试验检测单梁承载能力是公路工程中评定上部主要承重结构质量的主要手段，是检测试验室对上部结构承载能力进行检测的重要手段之一。在大部分检测项目中，现场检测结果的测量不确定度评定主要依赖于所采用的试验方法，试验方法不同，检测结果的测量不确定度也不相同。通过对静载试验应变检测过程中产生测量不确定度的来源进行分析，对测量结果进行了科学可靠的不确定度评定。

1 项目概述

(1)评定依据

依据《公路桥梁荷载试验规程》(JTG/T J21-01—2015)/第5章进行静态应变测试。

(2)主要测试仪器

DH3821电阻式静态应变仪、120Ω应变片、HC-10型锚杆拉拔仪

(3)测试对象

本次静态应变测试对象为本单位试验场8m普通钢筋混凝土T梁。梁高0.8m，顶板宽0.8m，C40混凝土浇筑，计算跨径7.7m。试验梁示意图见图1、图2。

图1 试验梁立面示意图(单位：mm)

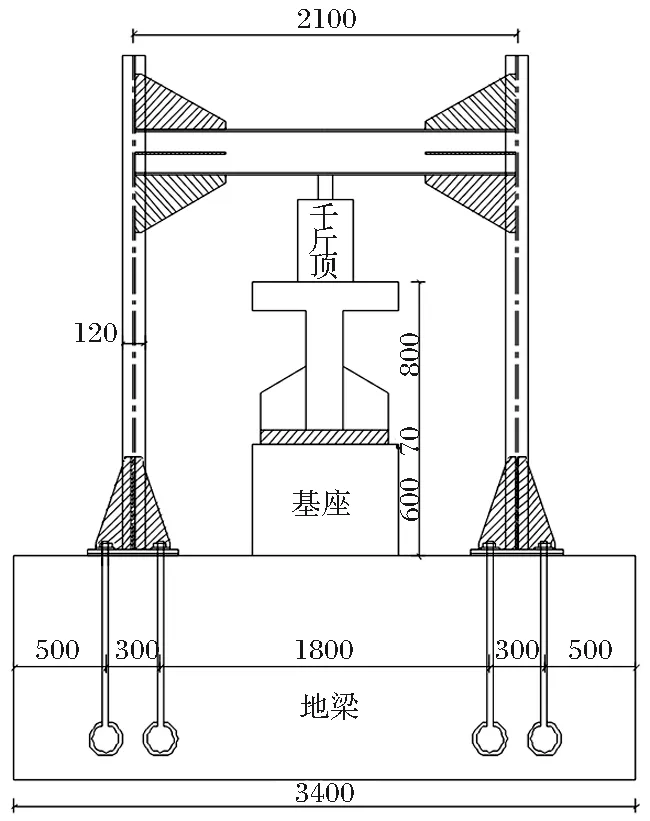
图2 试验梁横断面加载示意图(单位：mm)

(4)测试过程

本次静态应变测试采用千斤顶反力支架加载，共进行3次加载，加载截面为跨中A截面，试验荷载布置见图3。

图3 载位A荷载布置图

测试工况：跨中截面(A截面)应变和挠度试验。

测试截面布置示意图如图4所示。

图4 测试截面布置示意图(单位：m)

本次试验梁体设计内力设计荷载按公路—Ⅰ级，横向分布系数0.25考虑，即设计内力为118kN·m。试验荷载内力为115.5kN·m，试验荷载效率为0.98，满足《公路桥梁荷载试验规程》(JTG/T J21-01—2015)的要求(0.95<η≤1.05)[3]。

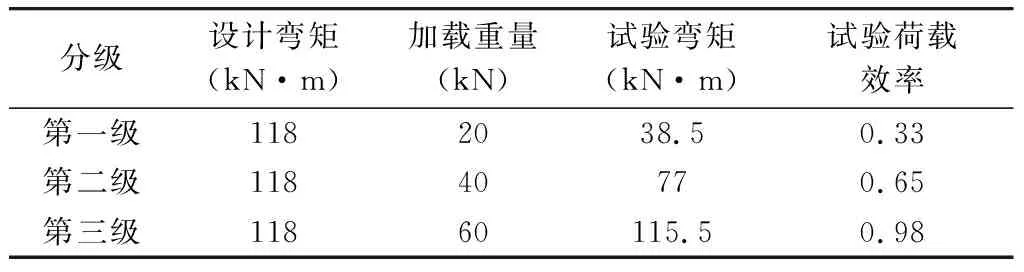
表1 载位A分级加载表

本次试验加载采用分级加载的方式，共分3级加载，1级卸载。静载试验各截面各加载工况实施程序如下[4]：

①初始状态(静载试验加载开始)→预加载→预加载卸载→读取测点初读数。

②千斤顶加压至20kN,维持数值不变，保持稳定后→读取试验数据。

③千斤顶加压至40kN,维持数值不变，保持稳定后→读取试验数据。

④千斤顶加压至60kN,维持数值不变，保持稳定后→读取试验数据。

⑤千斤顶卸载至0kN→读取测点卸载后读数(每个截面静载试验测试结束后，根据各测点的残余读数决定是否进行第二循环加载)[5]。

(5)测量原理

根据材料力学，梁体应变按(1)式计算：

其静态应变，根据胡克定律计算方法如下：

(1)

(2)

(3)

式中：M—千斤顶(HC-10型锚杆拉拔仪)加压力F产生的跨中弯矩；

F—千斤顶(HC-10型锚杆拉拔仪)加压力，即加载重量；

σ—梁底测试处加载重量产生的应力；

ε—梁底测试处加载重量产生的应变，即测试的静态应变；

W—截面抗弯抵抗矩，截面尺寸固定为常数；

E—梁体材料杨氏弹性模量，为常数。

静态应变测试主要测试的为弹性应变。

2 测量模型

检测结果可直接从设备检测数据中得出，因此测量模型采用综合评定法的模型，写为：

Y=X

(4)

式中：X—被测梁体跨中截面梁底应变测试值，με；

Y—被测梁体跨中截面梁底应变检测结果，με。

3 各项不确定度分析

由前述分析可以得出，静态应变测量不确定度计算模型主要由以下几个方面组成：

u=ua+ub1+ub2+ub3

(5)

式中：ua—应变测试重复性带来的不确定度；

ub1—应变片(120Ω应变片)灵敏度系数引起的不确定度；

ub2—应变测试仪器(DH3821电阻式静态应变仪)引起的不确定度；

ub3—应变测试加载荷载设备(HC-10型锚杆拉拔仪)带来的不确定度。

3.1 应变测试重复性带来的不确定度

同一人员操作同一台DH3821应变测试系统，对梁体跨中截面按最大加载60kN测试梁底静态应变10次，测量值如表1 所示。测量重复性引起的不确定度，属于A 类评定。根据A 类不确定度评定，取10个测量值的最大值作为测量结果，则:

表2 重复10次测量值分布表

3.2 应变片灵敏度系数引起的不确定度

采用电阻应变片测量静态应变，测试原理一般为惠斯通电桥。试验采用的1/4桥的连接方式，该测量仪器内部三线制1/4桥，为温度自补偿，暂不考虑温度影响。根据惠斯通电桥，假设测试应变片收到的应变为ε，则应变电桥的输出电压

(6)

式中：E0—惠斯通电桥初始电压；

Ky—应变片灵敏度系数。

惠斯通电桥输出电压经调理，接收到的电压

μ接收电压=Ksu电压输出=E0KsKyε

(7)

式中：Ks—DH3821应变测试系统调理发射接收的增益1000。

由式(6)可得：

(8)

因此,应变计算公式为：

(9)

其中E0、Ks均为常数项，应变片由于制造原因，其灵敏度系数存在不确定性，本试验所用的应变片的灵敏度系数为：Ky=2.2±1%，应变片灵敏度系数引起的绝对不确定度ub1计算如下：

(10)

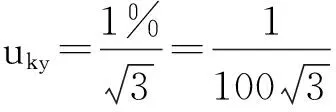
应变片灵敏度系数引起的相对不确定度：

3.3 应变测试仪器引起的不确定度

本次应变测量DH3821静态应力应变分析测试系统，经校准其准确度为0.5级，估计其分布为均匀分布，其准确性带来的相对不确定度uδ按B类评价

DH3821静态应力应变分析测试系统，其分辨力为1，区间半宽度为0.5，可将其估计为均匀分布，其带来的相对不确定度按B类评价

DH3821静态应力应变分析测试系统由其准确度和分辨力带来相对不确定度为：

3.4 应变测试加载荷载设备(HC-10型锚杆拉拔仪)带来的不确定度

HC-10型锚杆拉拔仪经校准，其相对扩展不确定度ur=0.39%，该设备相对不确定度按B类考虑：

3.5 合成标准不确定度

合成标准相对不确定度按下式计算：

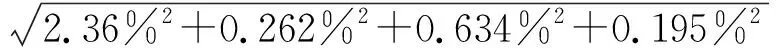
=2.465%

合成标准不确定度：u=ur×ε=2.465%×77.8=1.918με

3.6 扩展不确定度[2]

取包含因子k=2，置信区间95%，则扩展不确定度为

U=k×u=2×1.918=3.836με=3.9με

ε=77.8±3.9με，k=2

4 试验结论与建议

单梁静载试验是工程验收中一项重要的工作，按照规范建立了科学的数学模型，对测量不确定度的来源进行了逐步分析、逐项合成，评定了桥梁单梁静载试验检测结果的不确定度，最大限度地保证了检测结论的可靠性和准确性。通过对检测数据的分析，A类不确定度对测量结果的不确定度影响很大，占合成标准不确定度的95.7%，检测设备及其他影响因素对不确定度影响很小。但不确定度的评定方法不是唯一的，要根据行业要求、项目特点、被测对象特征、仪器设备的检校等各种因素综合考虑，建议遵循：考虑无遗漏，计算勿重复，主因应控制，次因可忽略的总体原则，才能切实做好不确定度的评定工作。