移动荷载作用下钢管拱桥动力特性分析

张志却，谢 凯，解文宗，李登国，卢彭真

(1.嘉兴市秀洲区交通建设投资有限责任公司 嘉兴市 314000； 2.浙江工业大学 杭州市 310013)

0 引言

钢管混凝土桥梁相比其他桥梁，具有独特的美学造型，在市政桥梁工程中被广泛应用。钢管混凝土因其钢管和混凝土相互作用，使其内部核心混凝土处于三项受压状态，提高了强度，并且使钢管结构的稳定性得以提升，两者相辅相成，使其材料性能和力学性能得以充分发挥，而且架设便利，施工快捷，经济效益高，因此这类结构在拱式体系桥梁中得到了快速而长远的发展[1]。随着我国钢材产量的不断增加，在桥梁的建造中加入钢材，不仅能够减少混凝土用量，减轻桥梁的自重，而且能够节约地方资源，保护环境，更加经济节约，对钢桥的发展起到促进作用。近年来，随着经济水平的提高和科学技术的不断发展，钢管混凝土拱桥的跨径不断攀升，并朝着轻型化方向发展，自重不断减小，致使钢管混凝土拱桥的动力响应问题日益突出[2-3]，因此这种桥梁的动力性能成为了时下研究的热点。桥梁结构的动力特性包括自振频率、振型、阻尼比等，这些参数是桥梁结构动力性能研究的重要依托，反映了桥梁结构的刚度指标[4]。然而目前研究有关此类桥梁动力性能较多，但针对动力特性的研究较少，因此亟待对这些拱桥的动力特性及其参数展开深入研究。

由于结构具有复杂的形式，钢管混凝土拱桥的自振特性各有其自身特点，通过改变桥梁的结构参数，调节其相应的数据，剖析相同结构参数或不同结构参数的改变对此类桥梁自振特性的影响[5-6]。评判桥梁承载能力的大小，桥梁结构工作性能的优劣，桥梁的动力特性分析非常重要。而移动荷载对桥梁结构的动力作用分析，是测试动力特性的关键因素之一，当车辆在桥上移动时，由于桥面凹凸不变、汽车发动机行驶过程中的震动等因素，会引起桥梁结构的振动，而且存在一个临界车速，当车辆在桥上的运动速度到达临界车速，会使桥梁结构的振动幅度达到最大，所以，为了有效控制桥梁结构的振动幅度，有必要对车辆的行驶速度进行限制，并分析移动荷载作用下桥梁结构的振动响应。

基于以上原理，以某钢管混凝土拱桥举例说明，采用ANSYS对其进行数值模拟计算，拟用550kN的移动常量力和五个不同的移动速度，来测试桥梁结构的振动，以此计算不同速度下拱顶和跨中位移时程曲线，钢管和混凝土内力及内力放大系数等，由此分析计算移动荷载对钢管拱桥动力特性的影响，这项工作将为钢管混凝土拱桥的抗震分析、风振和车振分析提供一定的依据。

1 工程概况与数值模型

主桥采用主跨为(30+80+30)m的飞鸟式钢管混凝土拱桥，桥梁全宽64.6m，左右分幅，单幅桥桥面宽32.2m。80m中跨结构形式为中承式钢管混凝土拱肋，拱肋截面形式为哑铃形钢管混凝土结构，矢跨比1/4，矢高20m；30m边跨结构形式为上承式钢筋混凝土拱肋，矢跨比1/7.5，矢高8m。桥梁立面图如图1所示。

图1 主桥立面示意图

采用ANSYS建立了钢管混凝土拱桥的有限元模型，在参考了过往有关钢管混凝土拱桥的有限元模型后[7]，主拱肋弦管采用哑铃型截面，主拱肋钢管及混凝土、横梁、纵梁、风撑、立柱等均采用Beam188空间梁单元来模拟，系杆、吊杆均采用link8单元来模拟，立柱、横梁之间采用combine14模拟，二期恒载、人行道栏杆和防撞护栏等桥面附属设施质量采用mass21单元模拟，钢管和混凝土单元之间采用共节点的形式建立，移动荷载采用550kN的移动常量力进行强迫振动分析。桥梁的模型示意图见图2。

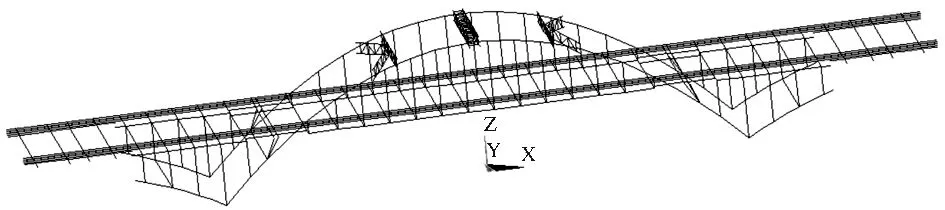
图2 全桥有限元模型

2 移动荷载作用下钢管拱桥动力响应及参数分析

ANSYS 程序提供了7种计算方法对结构的动力特性进行分析，分别为子空间法、分块Lanczos法、PowerDynamics法、缩减法、非对称法、阻尼法和QR阻尼法，其中以子空间法为优。根据有限元法原理，结合文献[8]中所介绍的方法，结构的三维自由振动方程可表示为：

Kx-ω2Mx=0

(1)

由式(1)可得：

(2)

x=XA

(3)

式中：x为结构振型向量；ω为结构自振频率；X为初始振型矩阵；A为待定列向量；M、K分别为结构的整体质量矩阵和整体刚度矩阵。

将式(3)代入式(2)得：

(4)

令：

K*=XTKX

(5)

M*=XTMX

(6)

于是：

(7)

K*A=ωM*A

(8)

本文的分析形式拟用550kN的移动常量力来进行桥梁强迫振动，移动常量力的行进速度分别为3.6km/h、18km/h、36km/h、54km/h。不同速度下拱顶和跨中位移时程曲线、钢管和混凝土内力及内力放大系数如图3及表1～表5所示。

从图3和这几个表中可以看出：

(1)随着速度的增大，跨中位移先增大后减小再增大，拱顶位移先增大后减小，跨中位移放大系数在1.022～1.028之间，拱顶位移放大系数在1.007～1.029之间，基本上在跨中位置位移达到最大。

图3 不同速度下拱顶和跨中位移时程曲线

表1 不同速度下跨中和拱顶位移峰值及放大系数

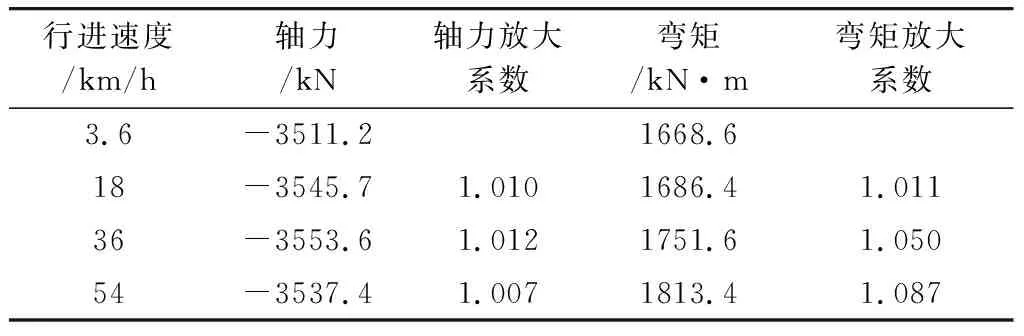
表2 不同速度下内侧拱肋钢管拱脚内力峰值及放大系数

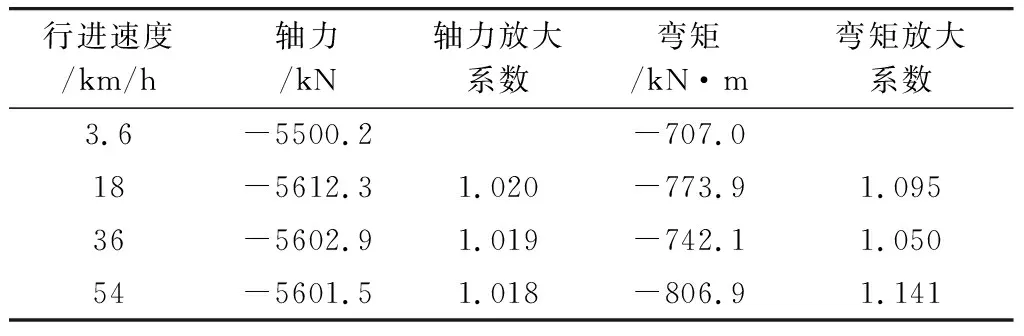
表3 不同速度下内侧拱肋混凝土拱顶内力峰值及放大系数

表4 不同速度下内侧拱肋钢管拱顶内力峰值及放大系数

表5 不同速度下内侧拱肋混凝土拱脚内力峰值及放大系数

(2)钢管拱脚轴力放大系数在1.007～1.012之间，钢管拱脚弯矩放大系数在1.011～1.087之间，说明速度动力效应对钢管拱脚弯矩的影响更大。

(3)混凝土拱顶轴力放大系数在1.018～1.020之间，混凝土拱顶弯矩放大系数在1.050～1.141之间，说明对速度动力效应对混凝土拱顶弯矩的影响更大。

(4)钢管拱顶轴力放大系数在1.018～1.020之间，钢管拱顶弯矩放大系数在1.037～1.158之间，说明速度动力效应对钢管拱顶弯矩的影响更大。

(5)混凝土拱顶轴力放大系数在1.008～1.014之间，钢管拱顶弯矩放大系数在1.017～1.097之间，说明对速度动力效应对混凝土拱脚弯矩的影响更大。

3 结论

由上述可知，移动荷载对桥梁结构的动力作用时，存在一个临界车速，当车辆在桥上的移动速度达到临界车速，会使桥梁结构的振动幅度达到最大，所以，为了控制桥梁结构在移动荷载作用下的振动幅度，必须对车辆的行驶速度进行限制。跨中位移放大系数在1.022～1.028之间，拱顶位移放大系数在1.007～1.029之间。钢管内力放大系数在1.008～1.011之间，混凝土内力放大系数在1.018～1.020之间。混凝土内力放大系数普遍大于钢管内力放大系数。