螺纹钢锚杆锚固岩石拉拔试验过程精细化数值模拟研究
2022-03-24刘亚鑫邢明录刘鹏程付彦坤
刘亚鑫,邢明录,刘鹏程,付彦坤
(1.山东科技大学 矿山灾害预防控制省部共建国家重点实验室培育基地,山东 青岛 266590;2.山东科技大学 能源与矿业工程学院,山东 青岛 266590;3.宁夏红墩子煤业有限公司 红二煤矿,宁夏 银 川 750000)
锚杆大量用于工程支护,为工程安全提供了保障[1]。锚固性能主要取决于锚固界面复杂的力学特性,其中界面失效是锚杆拉拔结构破坏的关键环节[2-3]。随着工程建设向深部转移,需要面对更为复杂的支护环境,对锚杆的要求也越来越高,而合理的锚杆外形参数能够有效地提高支护性能。
锚固段内的黏结是1种常见的接触问题,且呈现出1种与多因素相关的非线性行为。多年来,国内外众多学者利用理论分析、室内试验以及数值模拟,对锚固界面力学行为进行了研究。Farmer[4]发现在较小的拉拔载荷下,锚杆轴力和剪应力沿锚固长度方向指数衰减;尤春安等[5-6]认为锚杆拉拔结构的主要失效形式是锚固段内界面产生滑动破坏;Li等[7]引入1种特殊的界面模型模拟胶结材料,研究了锚杆界面脱黏破坏过程;Ren等[8]基于1种真实的灌浆-锚杆界面残余黏结强度的三线型黏结滑移模型,给出了预测灌浆岩石锚杆锚固力的解析解;江文武等[9]通过FLAC3D建立锚杆拉拔数值仿真模型,验证了数值模拟锚杆拉拔过程的可行性;赵同彬等[10]采用PFC2D软件模拟了岩石锚固段界面受力变形及破坏的特征;尹延春等[11]通过室内试验与细观颗粒流软件模拟研究了锚固段应力分布演化规律及其影响因素;Nemcik等[12]利用FLAC2D建立了张拉载荷的全灌浆岩石锚杆的数值模型,采用非线性黏滑关系研究了锚杆拉拔结构的相互作用;王晓卿等[13]通过FLAC3D的interface单元结合结构单元构建了仿真锚杆模型,提出了通过优化杆体外表形状提高锚杆黏结刚度的技术途径;任非凡等[14]采用ABAQUS对锚杆拉拔试验进行模拟,应用改进的Cohesive单元模拟复合锚杆的界面行为,对其锚固机理及传力机制进行全过程分析;Chang等[15]利用ABAQUS对锚杆拉拔过程采用二维平面建模研究,采用黏聚力模型模拟了锚杆-灌浆界面的界面行为。
随着锚杆精细化研究及计算机技术的发展,逐渐意识到锚杆表面的结构形状对界面锚固效果具有重要影响。Johnston和LAM等[16-17]试验发现规则的齿形界面和不规则的齿形界面的界面破坏有不同的影响,规则的界面凸起处几乎发生同时破坏,而不规则的界面凸起破坏具有明显的先后顺序;Bliimel等[18]、Overwin等[19]、Harris等[20]和Blumel等[21]发现横肋间距的存在影响锚固效果,进而影响锚固工程稳定性;荣冠等[22]发现锚杆与锚固剂的破坏发生位置主要在钻孔口和横肋位置,横肋参数对锚杆锚固性能具有极大的影响;Aziz等[23-24]通过拉拔试验验证了锚杆外形形状影响灌浆岩石锚杆的黏合能力,证明锚杆外形参数对锚固性能的影响。李东印等[25]和王伸等[26]基于ABAQUS软件研究螺纹钢横肋作用下的锚固体应力分布特征,验证螺纹钢横肋对锚杆锚固能力的影响;Cao Chen等[27-28]发现锚固体内部破坏面的产生和发展与锚杆横肋几何参数有关,提出锚杆与锚固剂接触的薄弱面。
这些研究证明横肋在锚杆拉拔结构载荷传递中起到了重要的作用,锚杆-岩体界面的相互作用是锚固性能的关键。为此,在上述研究的基础上,利用有限元软件ABAQUS,基于金属材料损伤模型、混凝土损伤模型及界面黏结损伤模型,进行螺纹钢锚杆拉拔数值模拟研究。
1 螺纹钢锚杆拉伸试验及模拟
1.1 锚杆真实弹塑性变形
试验锚杆为取自山东某矿使用的右旋螺纹钢锚杆,肋间距为12 mm。为获取螺纹钢锚杆真实力学参数,试验设备为材料试验机和轴向、纵向引伸计。采用瞬时面积法获得的锚杆的真应力-应变曲线,如图1。
1.2 螺纹钢锚杆拉伸试验模拟
采用有限元软件ABAQUS模拟单根锚杆拉伸断裂过程,锚杆采用延性金属损伤模型。锚杆材料弹性模量为210 GPa,泊松比为0.29。为准确模拟锚杆拉伸的塑性阶段,模拟参数以真实试验为基础,在图1的真应力-应变曲线上取点获得锚杆塑性参数,锚杆塑性参数取值见表1。锚杆断裂力学参数设置为:①断裂应变:0.3;②三轴应力比:0.33;③应变比:1。螺纹钢锚杆拉伸断裂过程应力云图如图2,锚杆拉伸的载荷-位移曲线如图3,不同横肋间距螺纹钢锚杆拉伸载荷-位移曲线图如图4。
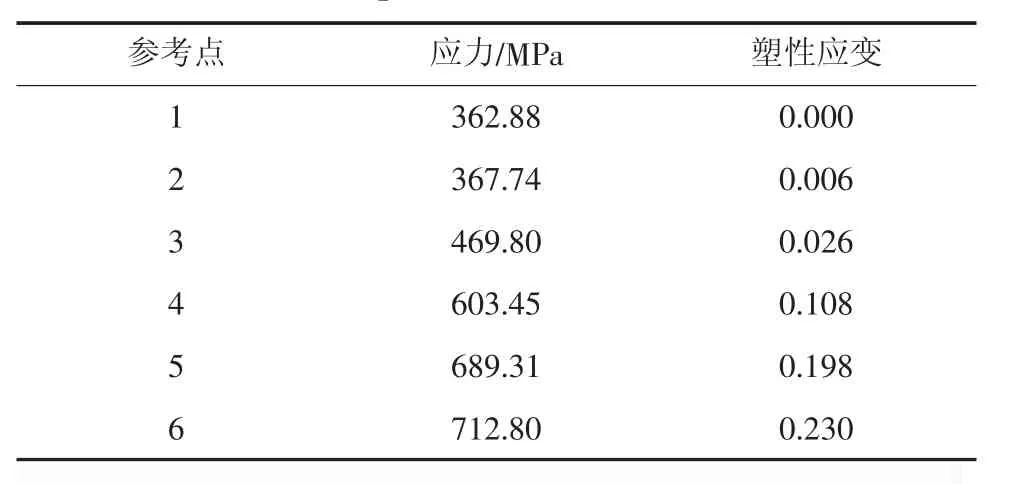
表1 锚杆塑性参数取值Table 1 Plastic parameter values of anchor rod
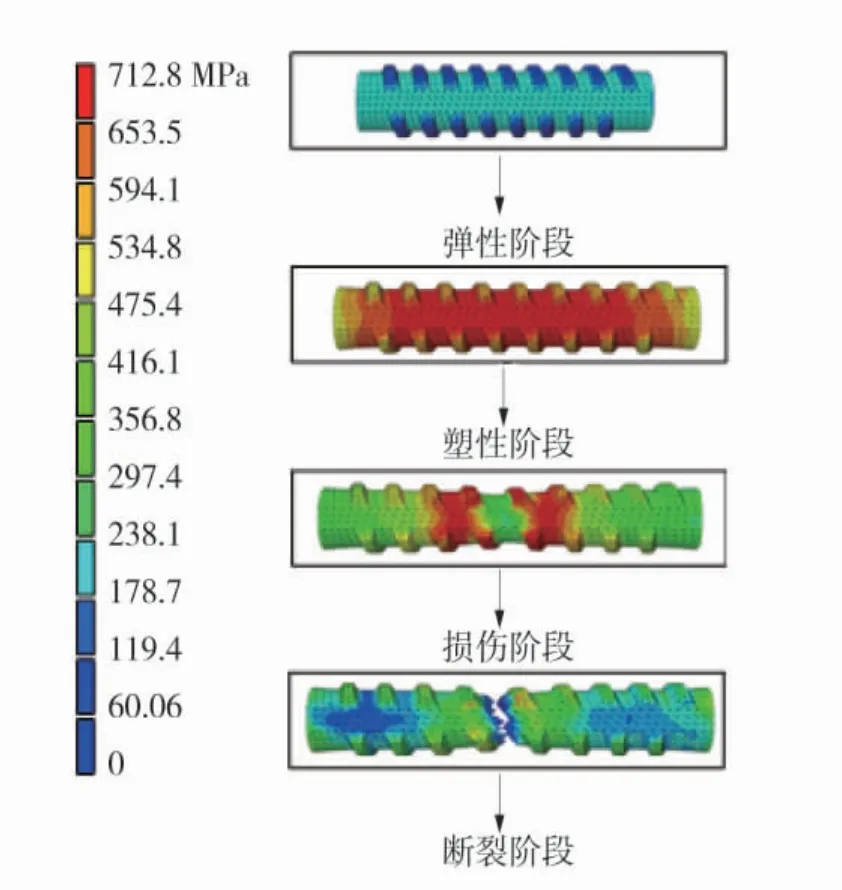
图2 螺纹钢锚杆拉伸断裂过程应力云图Fig.2 Stress diagrams of deformed steel bolt during tensile fracture
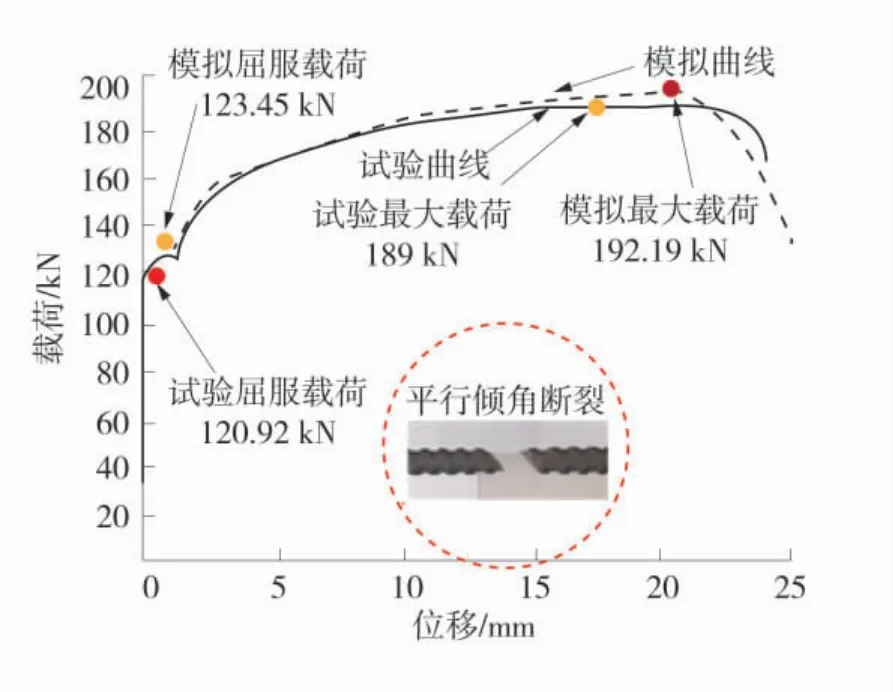
图3 螺纹钢拉伸试验及数值模拟载荷-位移曲线Fig.3 Load-displacement curves of tensile test and numerical simulation of deformed steel bolt
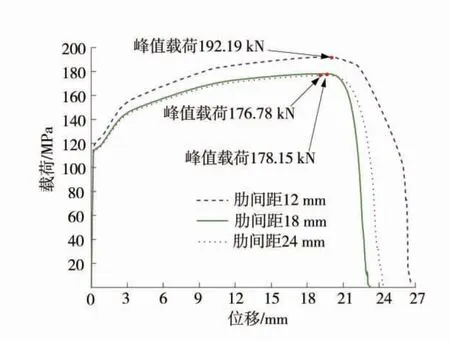
图4 不同横肋间距螺纹钢锚杆拉伸载荷-位移曲线Fig.4 Tensile load displacement curves of rebar anchor with different transverse rib spacings
从图2应力云图来看,可将锚杆拉伸分为弹性、塑性、损伤及断裂4个阶段。锚杆在弹塑性阶段沿杆体方向应力分布均匀,锚杆的某一局部范围内达到锚杆所能承受的最大载荷后,横向尺寸突然急剧缩小,载荷急剧降低,随着锚杆损伤逐渐累积,最终断裂。
图3载荷-位移曲线具有常规金属材料拉伸试验曲线的弹性、屈服、强化、局部变形4个阶段,最终锚杆平行于肋倾角断裂。对比图3中锚杆拉伸试验及模拟曲线可以看出,锚杆数值模拟断裂效果与拉伸试验一致。数值模拟所得锚杆屈服载荷、最大载荷等特征值与真实试验结果非常接近,曲线规律基本吻合,说明采用延性金属损伤模型可以模拟出螺纹钢锚杆拉伸试验断裂过程。
由图4可知,随着锚杆横肋间距的减小,螺纹钢锚杆最大拉拔载荷逐渐增大,这是因为螺纹钢锚杆表面横肋的存在,增加了等效横截面积,从而提升了锚杆拉拔载荷。
2 螺纹钢锚杆拉拔数值模拟模型
采用有限元ABAQUS软件建立锚杆拉拔的平面轴对称模型,螺纹钢锚杆模拟其真实横肋外形。锚杆横肋参数包括横肋间距、横肋高度、横肋宽度、横肋倾角等多个参数,研究以肋间距为变量进行数值模拟研究,锚杆横肋参数取值见表2。

表2 锚杆横肋参数取值Table 2 Parameter values of bolt transverse rib
数值模型如图5。所模拟螺纹钢锚杆直径为20 mm,长度为300 mm,锚固段长度为200 mm,岩体模型尺寸为φ100 mm×200 mm。锚杆和岩体均采用CAX4R四结点双线性轴对称四边形单元,整体模型网格单元个数为10 484。模型岩体右侧面(+x方向)采用固定边界条件,锚杆左侧(-x方向)设水平轴对称边界条件,在锚杆顶端施加拉拔位移(-y方向)。锚杆与岩体装配过程中采用布尔运算,使带肋锚杆与岩体接触面达到完全贴合装配。
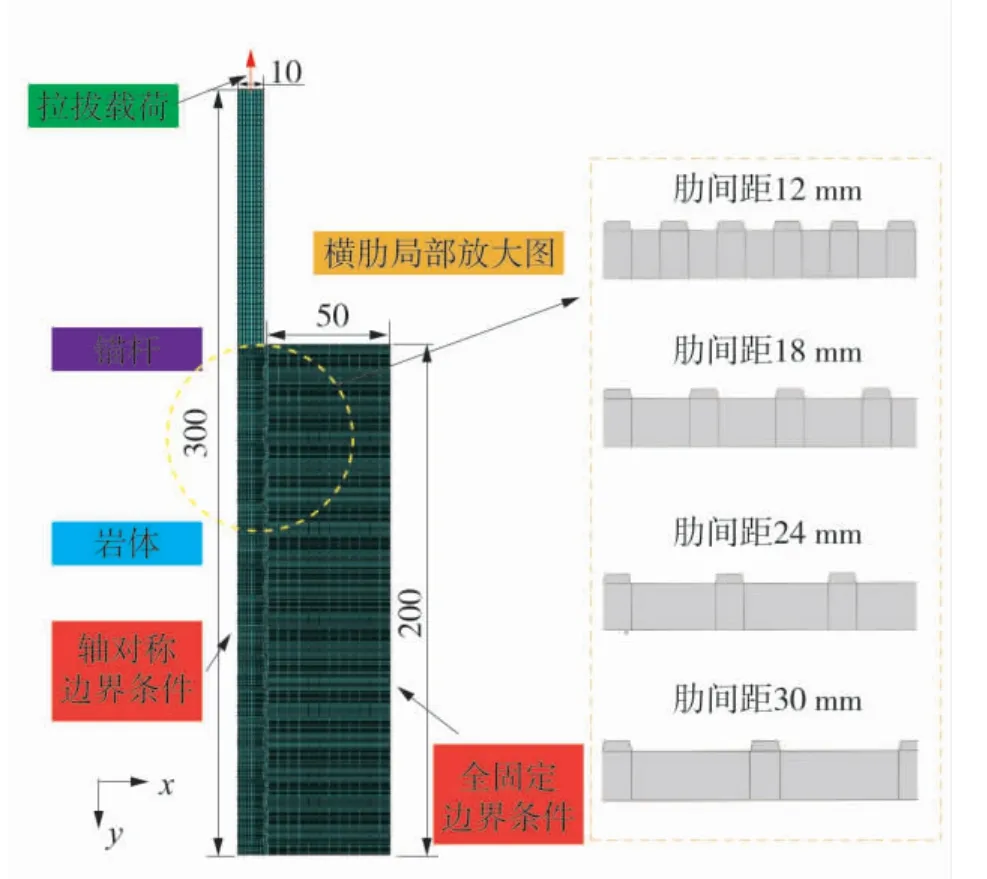
图5 锚杆拉拔数值模型Fig.5 Numerical model of bolt drawing
岩体本构选用混凝土塑性损伤模型,主要力学参数取值见表3。为了模拟岩体和锚杆之间的相互作用荷载传递,合理的界面接触模型的选择对于界面力学行为分析尤为重要。锚固界面设置为符合线性损伤演化规律的黏结损伤模型,界面应力达到损伤初始峰值应力后,黏结层开始损伤演化并最终分离、失效。黏结损伤模型参数取值见表4。
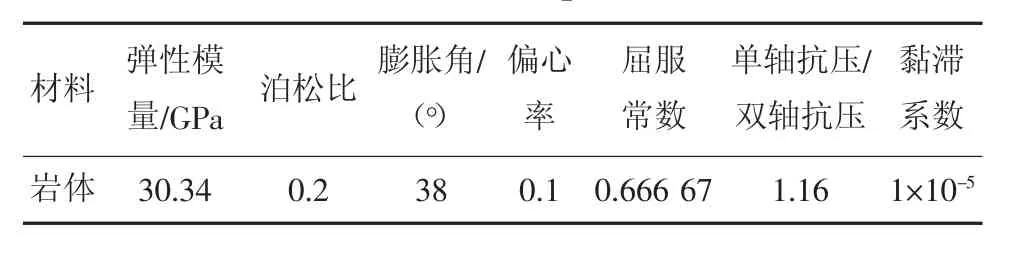
表3 岩体力学参数取值Table 3 Values of mechanical parameters of rock mass

表4 黏结界面损伤模型参数取值Table 4 Parameter values of bond interface damage model
3 模拟结果分析
3.1 锚杆拉拔载荷及失效分析
根据模拟得到不同肋间距锚杆的拉拔载荷-位移曲线图如图6。
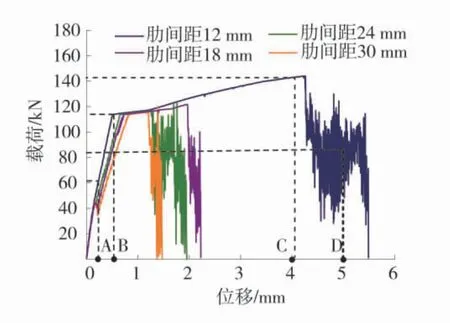
图6 不同横肋间距锚杆拉拔载荷-位移曲线图Fig.6 Drawing load displacement curves of anchor rod with different transverse rib spacings
由图6可以看出,肋间距分别为12、18、24、30 mm时,锚固极限承载力分别为149.80、121.69、116.63、115.48 kN。随着肋间距的增大,峰值载荷逐渐减小。锚杆拔出时,载荷-位移曲线会剧烈波动,肋间距为24、30 mm时,拉拔载荷-位移曲线在锚杆受力的弹性阶段已发生微弱波动,这是因为此时锚杆周围的岩体已产生破坏。对比分析表明,锚杆横肋的存在提高了界面黏结接触,增大了锚杆机械咬合力,肋间距越小,锚杆机械咬合力越大,合理改善横肋间距对提高锚固力具有增强作用。
图6中A点拉拔位移为0.25 mmm,B点拉拔位移为0.55 mm,C点拉拔位移为4.00 mm,D点拉拔位移为5.00 mm。为方便分析,选择肋间距12 mm的锚杆进一步研究。锚杆拉拔应力云图(肋间距12 mm)如图7~图10。
由图7~图10可知,当位移加载到0.25 mm时,锚杆载荷为60.5 kN,锚杆横肋及岩体接触肋角位置产生应力集中区,锚杆应力峰值为220.6 MPa,岩体端部肋角发生破坏,岩体应力峰值为15.8 MPa;当位移加载到0.55 mm时,锚杆载荷为114.0 kN,锚杆应力峰值为364.0 MPa。岩体与锚杆肋接触面的应力集中区逐渐向深部传递,岩体应力峰值为28.4 MPa,锚杆-岩体界面在端头部位开裂;当位移加载到4.00 mm时,锚杆载荷为142.9 kN,锚杆锚固承载力达到峰值,锚杆应力峰值为483.6 MPa,岩体应力峰值为36.1 MPa。界面开裂逐渐向岩体深部扩展延伸,锚杆拉拔结构整体破坏范围增大。岩体呈漏斗状由浅部向深部逐渐变形、破坏。锚杆载荷-位移曲线的微小波动也是周围岩体损伤的证明;当位移加载到5.00 mm时,锚杆载荷-位移剧烈波动,表征锚杆-岩体界面及岩体本身正在剧烈破坏,岩体界面应力峰值移动到锚固段中后部,且可观察到锚杆横肋上也有损伤,单元失效,但锚杆仍具有残余锚固强度,约为极限承载力的1/2。继续拉拔则锚杆被拔出,完全失效,承载力逐渐降低至0。
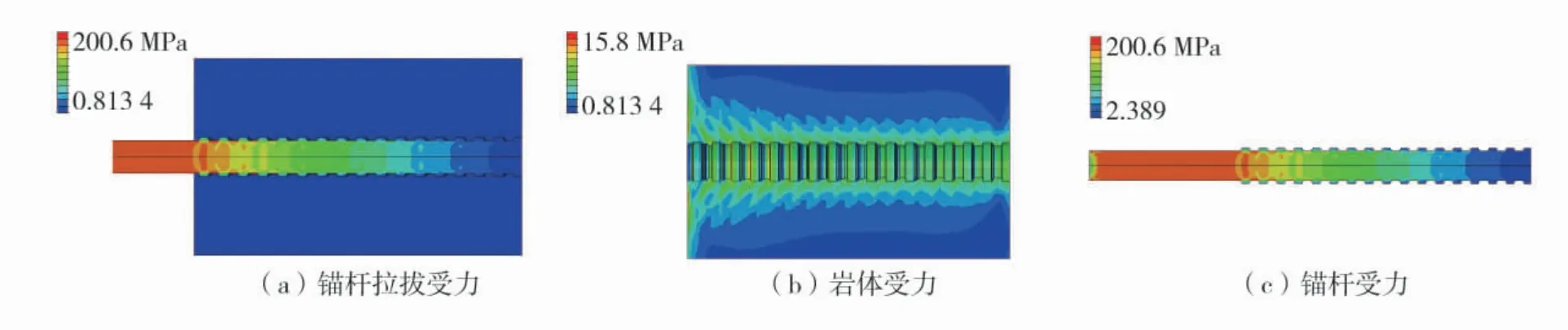
图7 拉拔位移0.25 mm时锚杆拉拔应力云图Fig.7 Cloud diagrams of anchor rod drawing when drawing displacement is 0.25 mm
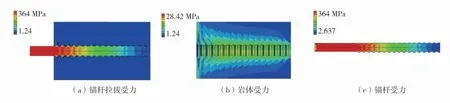
图8 拉拔位移0.55 mm时锚杆拉拔应力云图Fig.8 Cloud diagrams of anchor rod drawing when drawing displacement is 0.55 mm

图9 拉拔位移4.00 mm时锚杆拉拔应力云图Fig.9 Cloud diagrams of anchor rod drawing when drawing displacement is 4.00 mm
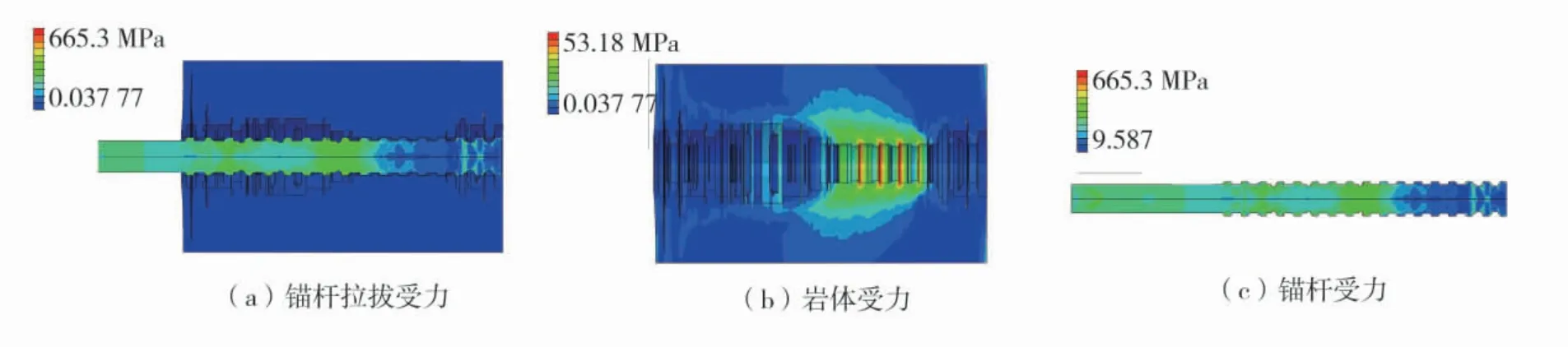
图10 拉拔位移5.00 mm时锚杆拉拔应力云图Fig.10 Cloud diagrams of anchor rod drawing when drawing displacement is 5.00 mm
3.2 锚杆拉拔黏结界面力学特性
肋间距12、18、24、30 mm锚杆的轴向应力沿锚固轴向分布曲线如图11和图12。
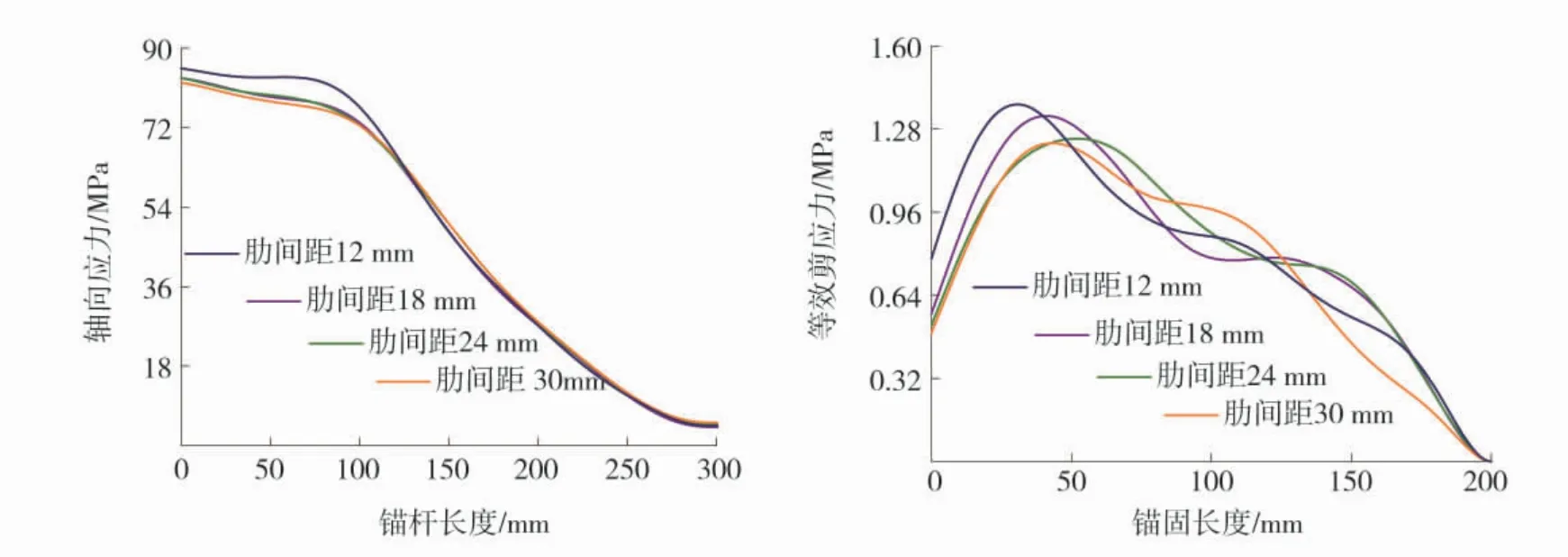
图11 拉拔位移0.075 mm时锚固界面应力分布Fig.11 Stress distribution of anchorage interface when drawing displacement is 0.075 mm
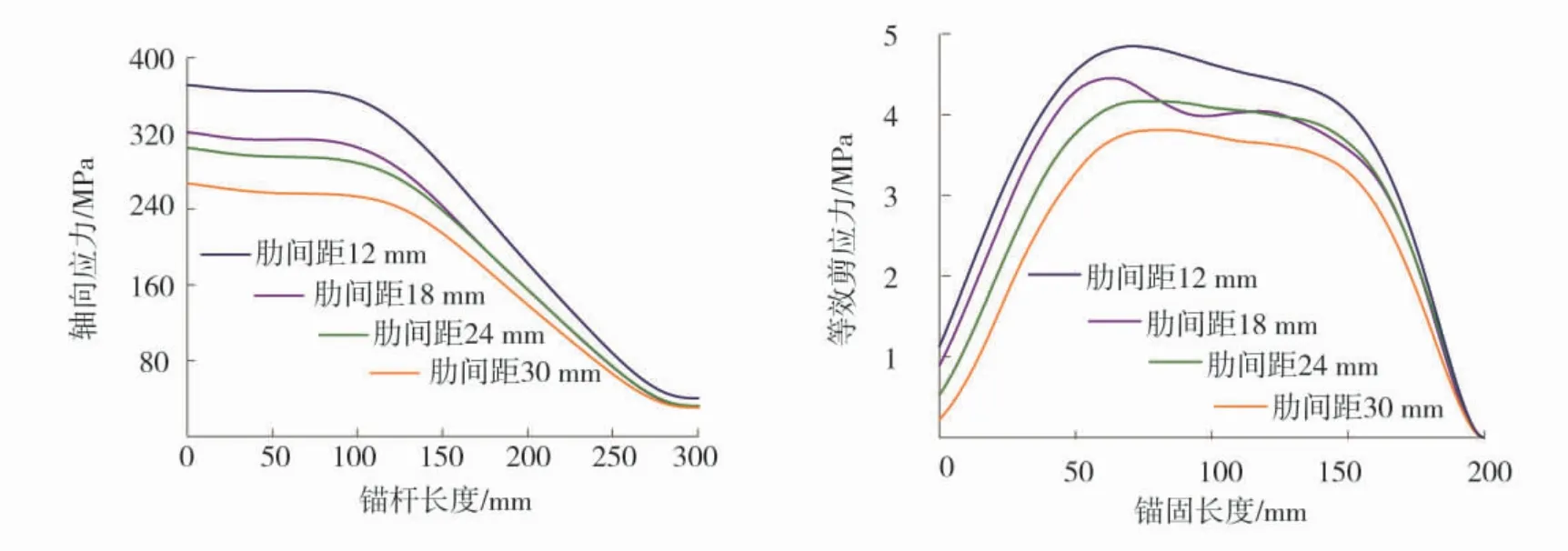
图12 拉拔位移0.55 mm时锚固界面应力分布Fig.12 Stress distribution of anchorage interface when drawing displacement is 0.55 mm
由图11和图12可知,不同肋间距锚杆的轴向应力分布规律基本相似,锚杆自由段的轴力最大,锚杆轴向应力沿锚杆长度方向逐渐指数衰减;锚杆轴向应力与锚杆表面剪切应力之间的关系,通过考虑锚杆1个小单元上的应力平衡方程,得到界面等效剪切应力表达式为:
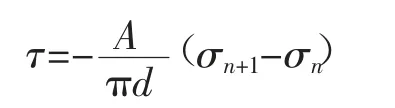
式中:τ为等效剪应力;A为锚杆横截面积;d为锚杆的直径;(σn+1-σn)为锚杆单元轴向应力差值。
根据等效剪应力公式可获得锚杆等效剪应力沿锚固长度方向的分布规律,结合图11和图12可知:当拉拔位移为0.075 mm时,锚杆处于弹性阶段,岩体也未发生损伤,锚杆剪应力沿锚固长度呈先上升后迅速衰减的趋势,由于横肋应力集中的影响下降段有些许波动;当拉拔位移为0.55 mm时,剪应力峰值随载荷的增加逐渐向深处转移,沿锚固长度呈先上升、后平稳衰减、再急速下降分布,周围岩体发生损伤导致曲线产生波动。通过对比不同肋间距锚杆界面应力分布曲线可以看出,锚杆肋间距越小,岩体提供给锚杆的轴力和剪应力越大。锚杆肋的存在有助于提高锚固承载力。
3.3 锚杆拉拔横肋表面应力分析
针对锚杆单个横肋进行分析,取锚杆微元段分析其单元受力情况,梯形横肋共有3个表面,且从第1个横肋开始,表面编号为1-1(第1个肋前表面)、1-2(第1个肋上表面)和1-3(第1个肋后表面),后面每个肋上的命名以此类推,锚杆横肋表面示意图如图13。
选取图13中的锚杆表面(沿着肋角的锚杆杆体表面),得到的锚杆表面轴向应力和剪应力沿锚固长度分布曲线图如图14和图15。
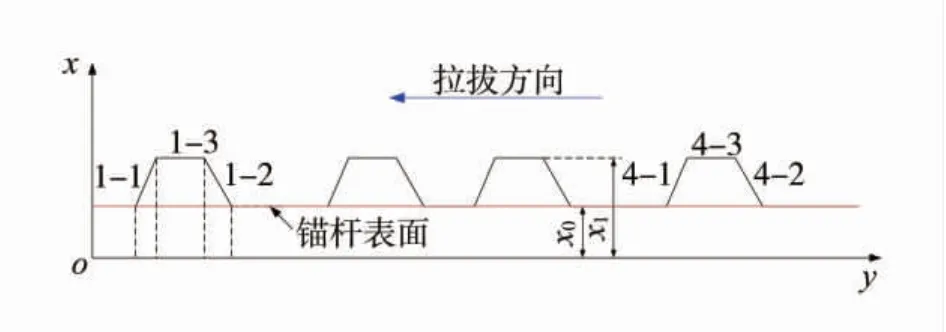
图13 锚杆横肋表面示意图Fig.13 Schematic diagram of bolt transverse rib surface
从图14、图15中可以看出,锚杆表面由于受到横肋的影响而引起局部应力急剧增大,所以在锚杆表面每隔1个肋均会在肋角产生1个应力集中区,而两肋中间区域应力就迅速降低。锚杆横肋处轴向应力及剪应力沿锚固长度呈锯齿状周期性衰减分布。通过对比不同肋间距锚杆表面应力分布曲线可以看出,随着肋间距的增大,轴向应力及剪应力逐渐减小,肋间距为12 mm时应力值最大。分析其原因为,肋间距越小的锚杆,等长度范围内的表面横肋数量较多,单位长度范围内的等效黏结面积及机械咬合力较大。锚杆肋与岩体机械咬合作用明显,锚杆剪应力反作用于岩体上,因岩体抗剪强度较低,故岩体与锚杆肋耦合的部分逐渐发生剪断破坏。峰值剪应力总是最先出现在锚固段首个横肋附近,说明锚固表面脱黏或岩体剪切破坏发展模式为由锚固浅部向深部逐渐推进,表现出渐进失效的特征。
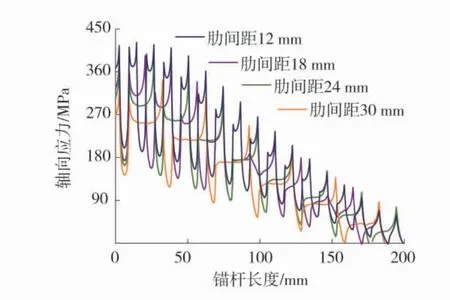
图14 锚杆表面轴向应力沿锚固长度分布曲线图(拉拔位移0.55 mm)Fig.14 Distribution curves of axial stress on bolt surface along anchorage length(drawing displacement of 0.55 mm)
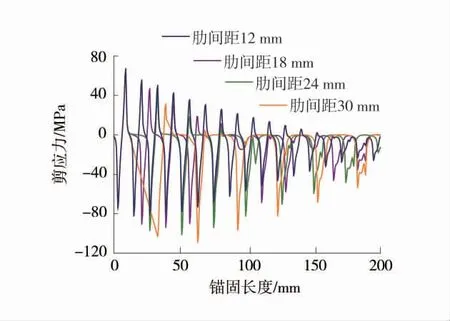
图15 锚杆表面剪应力沿锚固长度分布曲线图(拉拔位移0.55 mm)Fig.15 Distribution curves of bolt surface shear stress along anchorage length(drawing displacement of 0.55 mm)
选取锚固段每个横肋表面1(面1-1、2-1、…、n-1)、表面3(面1-3、2-3、…、n-3)上的剪应力,得到的 锚杆肋表面1沿锚固长度方向的剪应力分布曲线如图16,锚杆肋表面3沿锚固长度方向的剪应力分布曲线如图17。
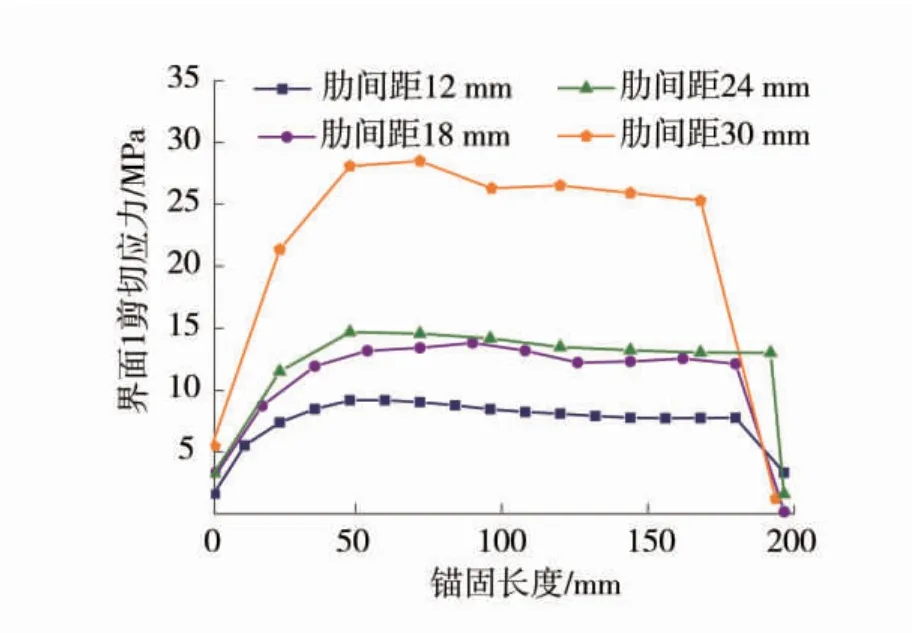
图16 锚杆肋表面1沿锚固长度方向剪应力分布曲线图(拉拔位移0.55 mm)Fig.16 Shear stress distribution curves of anchor rib surface 1 along the anchorage length direction(drawing displacement of 0.55 mm)
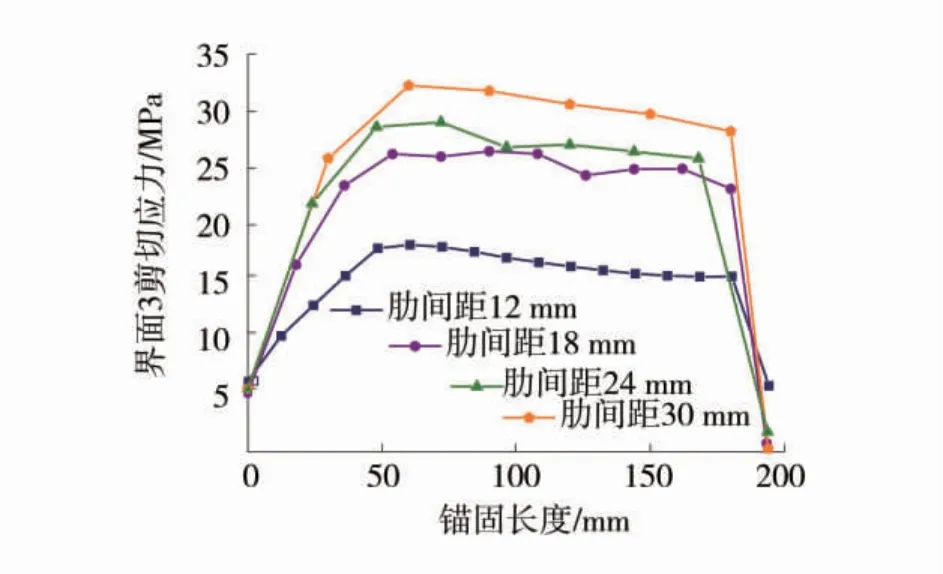
图17 锚杆肋表面3沿锚固长度方向剪应力分布曲线图(拉拔位移0.55 mm)Fig.17 Shear stress distribution curves of anchor rib surface 3 along the anchorage length direction(drawing displacement of 0.55 mm)
由图16和图17可以看出,肋表面剪应力沿锚固长度方向的分布规律与图12给出的等效剪应力的分布规律基本一致。表面3的剪应力值大于表面1,说明表面3相对于表面1更容易发生剪切损伤。由于锚杆横肋各表面剪应力值的差异性,可考虑在设计锚杆时对横肋的形状进行优化设计,使得各肋接触表面的破坏条件具有相对的等强度性。
4 结 论
1)基于延性金属损伤模型,模拟螺纹钢锚杆杆体拉伸断裂过程,所得锚杆屈服载荷、最大载荷等特征值与真实试验结果非常接近,载荷-位移曲线规律基本吻合,有效还原真实锚杆拉伸试验的弹性、塑性、损伤及断裂过程。与圆钢材料拉伸断裂特征不同,试验与数值模拟发现锚杆横肋会对锚杆拉断特征产生影响,锚杆拉伸断裂方位与肋倾角平行。
2)模拟所得不同肋间距锚杆拉拔载荷-位移曲线变化规律证明,锚杆肋间距越小,锚固承载性能越好。锚杆横肋的存在可有效增加界面黏结接触面积,增强锚杆机械咬合作用,合理改善锚杆横肋参数对提高锚固力具有增强作用。
3)锚杆轴向应力沿锚杆长度方向呈指数衰减分布。锚杆处于弹性阶段,且岩体未破坏前,锚固界面等效剪应力沿锚固长度呈先上升后迅速衰减的趋势;岩体破坏后,等效剪应力沿锚固长度呈先上升、后平稳衰减、再急速下降分布,界面损伤及剪应力峰值逐渐向锚固段深部移动。
4)由于横肋的存在,锚杆杆体表面轴向应力及剪应力沿锚固长度方向呈锯齿状周期性衰减分布,肋表面3相对于表面1更容易发生剪切破坏。由于锚杆横肋各表面剪应力值的差异性,在设计锚杆时可考虑对横肋的形状进行优化设计,使得锚固剂与肋不同表面的黏结破坏条件具有相对的等强度性。
