行业网络关联度及其对股市下跌风险的影响

■周 亮

一、引言

网络关联度常被用来识别不同经济个体间的相互关系。当网络关联度越高时，经济个体间的关系更为复杂，联系更为紧密。当某个经济个体（尤其是在网络中重要性较高的个体）出现问题的时候，风险很容易通过网络传导至其他经济个体上，从而导致其他较为脆弱的经济个体出现问题。衡量网络关联度的方法较多，代表性的包括Billio et al.（2012）利用格兰杰因果网络提出的动态因果指数（DCI）、Diebold和Yilmaz（2012）基于广义误差方差分解提出的信息溢出指数法。通过借鉴系统性金融风险的衡量指标和方法来对股市整体的数据进行分析，可以对股市整体的系统性风险进行识别，并为投资者的风险识别与管理提供有益的帮助和借鉴。

考虑到网络关联度不仅可以将其作为单一指标研究其动态特征及对市场整体的影响，还可以通过研究网络的内部结构识别各行业的风险溢出状况。基于此，笔者拟利用申万行业指数收益率及波动率构造我国股市行业层面的网络关联度，并试图从以下三个方面详细研究行业网络关联度的动态特征及其对股市下跌风险的影响：第一，网络关联度的动态特征如何？风险较高的时间节点的网络关联度是否明显高于风险较低的时间节点？第二，不同行业在网络中的特征是否有显著差异？哪些行业在系统中的重要程度更高？第三，网络关联度是否能够对未来的股市下跌风险进行预测，从而为投资者的风险管理提供有益借鉴？

二、文献综述

自资本资产定价模型（Sharpe，1964）提出以来，学者们对不同风险因子的定价能力进行了深入研究，最具代表性的是三因子模型（Fama&French，1992），通过市场、规模及估值三个因子可以很好地解释股票的横截面收益差异。除此以外，动量因子、流动性因子、质量因子、波动率因子、盈利因子和投资因子等都被证明具有显著的定价能力。还有学者从股市下跌风险角度识别可预测的因子或因素，如Huang & Wang（2009）发现内生的流动性需求可以引起股票收益的负偏和厚尾，从而引发缺乏任何冲击的股市暴跌。刘桂荣（2017）发现投资者情绪与股市下跌风险正相关，并且投资者情绪的悲观变动比乐观变动对股市下跌风险的影响更大。吕大永和吴文锋（2019）从流动性角度进行了相关研究，发现杠杆融资交易量及其波动均显著加剧了标的股价的下跌风险。可以看到，在对市场下跌风险的研究中，流动性问题是学者们关注的焦点，实际上，网络关联度所代表的系统性风险也包含了股市下跌风险的预测信息，股市中各行业或各企业的联动性很强，表现为具有较强的网络关联度，当网络关联度发生异动时，往往也能对股市的下跌风险进行预测。

网络关联度在金融领域常被用来对系统性金融风险衡量和对系统重要性金融机构进行识别，如Li&Giles（2015）采用多元GARCH模型测算各市场或机构间收益率或波动率的相关性，但是多元GARCH 模型并不能很好地捕捉风险的动态变化特征（Barunik et al.，2016），因此Kritzman et al.（2011）基于主成分分析法提出了信息吸收比率，Diebold & Yilmaz（2012）基于广义误差方差分解提出了信息溢出指数法，以及Billio et al.（2012）利用格兰杰因果网络提出了动态因果指数（DCI），可以对风险的动态性进行更有效的分析。周亮和李红权（2019）验证了信息溢出指数及格兰杰因果网络在识别中国大陆系统性金融风险的有效性。也有部分学者将金融风险指标作为市场系统性风险对待，如陈湘鹏和何碧清（2019）采用金融巨灾风险指标对中国股市的横截面收益进行了定价。但是到目前为止，还较少有文献研究网络关联度对股市未来收益率或者下跌风险的影响。考虑到系统性风险的累积往往预示着市场收益率下行的可能性增加，因此网络关联度的上升很可能会导致股市下跌风险的增加。

基于此，本文拟采用格兰杰因果网络及信息溢出指数构造我国股市的行业网络关联度指标，在分析其动态特征及各行业在网络中不同表现的基础上，利用Logit 等模型考察行业网络关联度对股市下跌风险的影响，以为投资者的风险管理提供经验借鉴。相对于其他学者的研究，本文的主要创新之处在于：一方面，利用网络模型研究了我国A股行业间的动态网络关联特征，并分析了关联度较高时各行业对外风险的溢出特征，识别出系统重要性行业。另一方面，通过建立Logit模型，研究了系统网络关联度及行业对外风险溢出度对股市下跌风险的预测能力，可以为金融投资实践及风险管理提供有益的借鉴。

三、研究设计

（一）网络关联度衡量指标

1.格兰杰因果网络指数（DCI）

借鉴Billio et al.（2012）的方法利用股市的行业指数来构造市场的整体网络关联度。假设系统中有N 个行业，则定义行业j 到行业i 的信息溢出Iij为：

则可以用整体的信息溢出度来衡量系统的网络关联度，计算公式为：

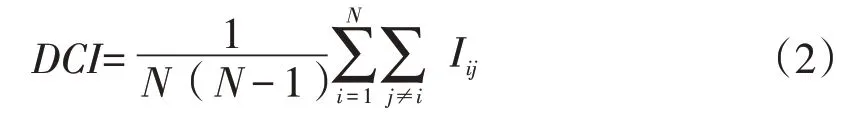
同样可以定义单个行业对整个系统的影响程度，包括对外溢出（out）和接受溢出（in）两个方面，如公式（3）所示：

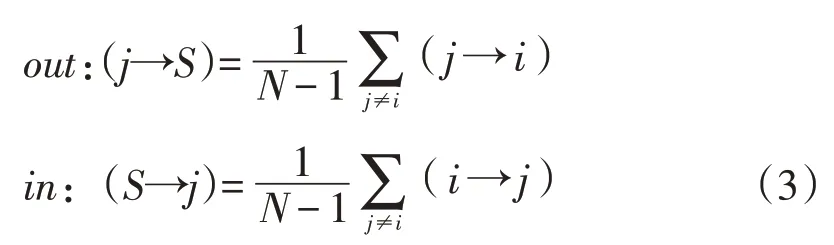
通过对单个行业对外溢出和接受溢出的分析，则可以对行业的相对影响力进行评估。

2.信息溢出指数（Spillover）

参考Diebold&Yilmaz（2012）方法来研究金融机构间的信息溢出关系，第j 个变量的结构冲击对第i个变量滞后H阶方差变化的贡献度：

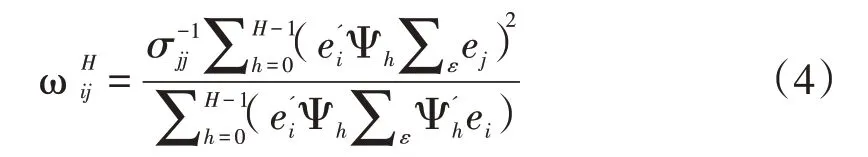
在公式（5）的基础上就可以定义总信息溢出值为变量间的方差分解贡献度对总方差的贡献，可以用其来对系统的网络关联度进行衡量，计算公式为：

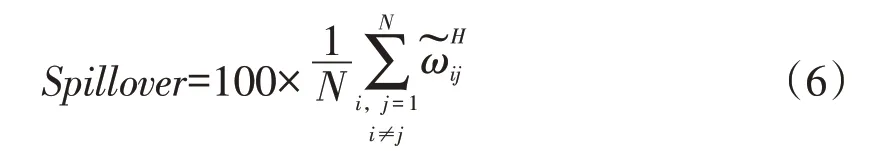
（二）回归模型

通过建立回归模型探讨网络关联度对股市下跌风险的预测能力。分别建立OLS和Logit回归模型如式（7）和式（8）所示：

其中，Rt+1为下一期Wind 全A 指数收益率；Net为网络关联度，包括DCI和Spillover 两种，由于基于收益率计算的指标包含的信息含量更多，因此这里仅考虑基于收益率计算的DCI 和Spillover，DCI 进行差分表示变化率，Spillover 进行对数差分表示变化率；Xt为一系列控制变量，笔者选择了工业增加值环比、CPI 环比、M2、10年期国债到期收益率、市场总换手率以及市场波动率作为控制变量；Rt为当期的指数收益率，用来控制市场收益率的自相关性。Logitt+1为逻辑回归变量，代表股市的下跌风险，样本区间内Wind 全A 指数收益率的均值为0.29%，最小值为-37.16%，发生在2009 年8 月，Q（0.1）、Q（0.2）和Q（0.3）分别为-8.6%、-5.3%和-2.7%，因此本文首先将Logitt+1设定为“当Rt+1＜-2.7%时取1，否则为0”，后续稳健性检验中将-2.7%分别替换成-5.3%和-8.6%进行分析。

同时本文还考虑了市场状态可能对网络关联度预测能力的影响，因此设置了Market和Sent两个虚拟变量。其中Market 是牛熊市指标，借鉴Cooper et al.（2004）等学者的研究，如果指数当月收益率大于过去3年的月度收益率均值时，定义为牛市，此时Market 取1；反之则定义为熊市，此时Market 取0。由于需要用到3 年的滚动样本，因此Market 指标是从2003 年1 月开始。借鉴高大良等（2015）方法，提取新增投资者开户数、市场换手率、封闭式基金折溢价、波动率等4个指标的第一主成分作为Sent代理变量，所有指标均采用经工业增加值和CPI 回归后的残差进行分析。当Sent 大于其序列中位值时设定为1，否则为0。由于部分情绪源指标均在2011年后才有数据，因此Sent 指标是从2011 年1 月开始。同样建立回归模型验证网络关联度与市场状态的交互作用，如式（9）和式（10）所示：

其中，Yt+1为Rt+1或Logitt+1，β1反映熊市或者低情绪期网络关联度对股市下跌风险的预测能力，β1+β2反映牛市或者高情绪期网络关联度对股市下跌风险的预测能力。

（三）样本选取

为避免因个股上市时间并不一致，且不同行业上市公司数量差异较大而导致的行业偏差问题，本文选择了申万一级行业指数作为研究对象。申万一级行业指数将全部A 股上市公司分为了食品饮料、医药生物、家用电器等28个行业，绝大部分指数均是2000年开始对外发布，样本的横截面数量和时间跨度均较为理想。因此最终选择2000 年1 月—2020 年2 月所有行业指数的日数据进行分析，共包括4883个交易日。

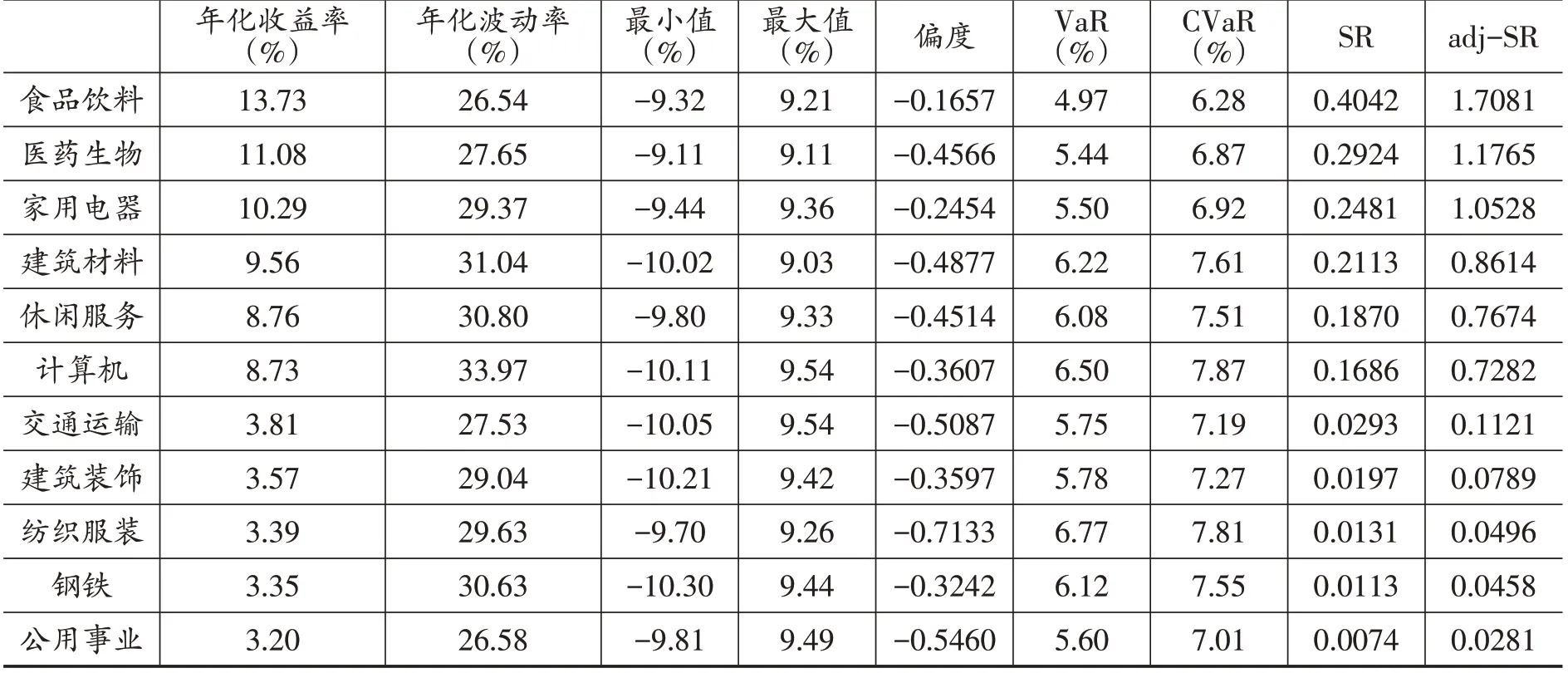
表1 行业收益率描述性统计

四、实证检验结果

（一）描述性统计分析

表1 报告了行业日收益率的描述性统计结果（限于篇幅，仅报告了年化收益率排名前10的行业），可以看到，食品饮料行业在样本区间获得了最高的年化收益率，同时其年化波动率在所报告的10个行业中也是最低的。除了用年化波动率来衡量风险，表1还报告了衡量尾部风险的VaR（在险价值）和CVaR（条件在险价值）。从表1可以看出，食品饮料行业的尾部风险同样是最低的，由于收益最高，风险最低，因此食品饮料行业的夏普比率（SR）达到了0.4，远超其他行业。同时本文借鉴黄金波等（2018）等学者的研究，用CVaR 替换了夏普比率的标准差，构造了调整夏普比率（adj-SR），从而可以更好地对尾部风险调整后收益进行衡量。结果显示，食品饮料行业的adj-SR 达到了1.71，远高于其他行业。除了食品饮料行业外，医药生物和家用电器的adj-SR也超过了1，说明这两个行业也具有较高的风险调整后收益，而其他行业的表现就相对要差很多了。

（二）网络关联度特征分析

1.网络关联度的动态特征

分别采用行业指数收益率和波动率来构造DCI 和Spillover 指标来衡量市场的网络关联度。其中，波动率采用的是GARCH 波动率，对日收益率序列建立ARMA（1，0）-GARCH（1，1）模型得到每天的GARCH 波动率序列，再利用公式（1）-（6）建模。滚动窗口设定为250 日（即一年的交易时间），即利用t-249日至t日的数据来计算第t日的DCI和Spillover 指标值。计算出每天的网络关联度指标值后，再将每个月内的所有日数据进行平均，则可以得到最终用来分析的月度网络关联度指标值。由于用到了一年的滚动窗口，因此实际得到的网络关联度指标值是从2001年1月至2020年2月。

表2 网络关联度指标描述性统计

表2 报告了网络关联度指标值的描述性统计结果，其中Q（0.25）表示25%分位数，AR（1）表示一阶自相关系数，其他以此类推。可以看到，因为计算方法上的差异，DCI（基于收益率计算）和DCI_Vol（基于波动率计算）均在0.5 以下，而Spillover（基于收益率计算）和Spillover_Vol（基于波动率计算）均在80以上，说明不同行业间的信息溢出较为紧密，但真正能够构成格兰杰原因的较少，两个指标虽然都可以用来分析网络关联度，但所表达出的内容是存在着差异的。从自相关系数看，无论是DCI还是Spillover 均表现出了较强的自相关性，一阶自相关系数均在0.9 以上（DCI 略低于0.9），且5 阶自相关系数也均在0.47 以上，而即使到了10 阶，Spillover 的自相关系数仍然达到0.24，说明网络关联度具有内在稳定性。

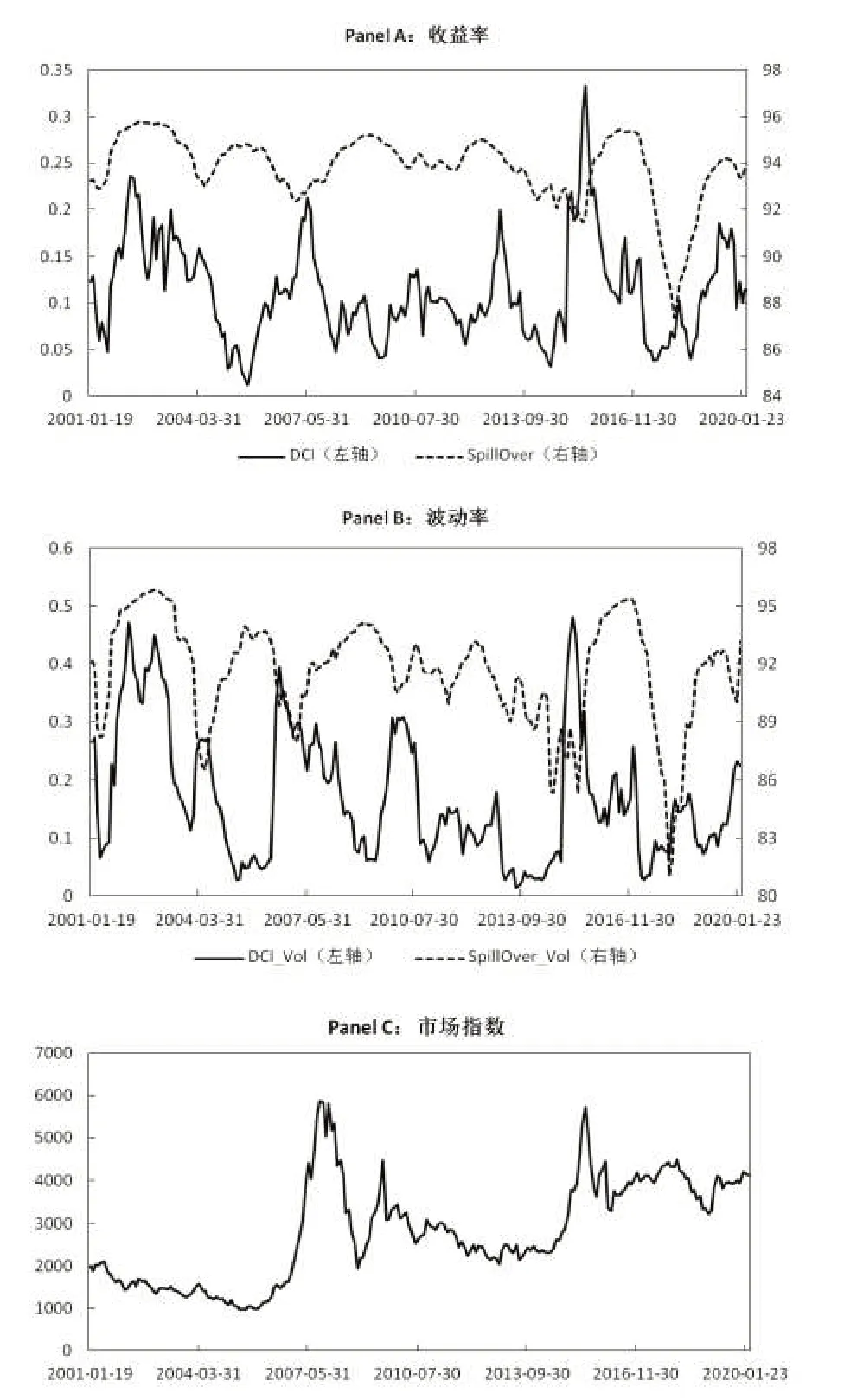
图1 网络关联度动态走势图

为更清晰地观察网络关联度的动态走势，图1 展示了网络关联度的动态走势图。其中Panel A 是基于收益率计算的DCI 和Spillover 指标的走势图，Panel B是基于GARCH波动率计算的DCI_Vol 和Spillover_Vol 指标的走势图，为进行比较分析，Panel C 展示了Wind 全A 指数在样本区间的走势图。可以看到，无论是基于收益率还是基于波动率，DCI 都比Spillover 波动略为剧烈，同时通过与Wind 全A 指数的比较发现，DCI对股市顶底的预测作用似乎更明显，无论是基于收益率的DCI 还是基于波动率的DCI_Vol，均在2007 年和2015 年两次股灾前达到了阶段性的峰值，而Spillover 的预警作用要差很多，甚至表现出了与市场指数相反的趋势。再次说明了两种方法在衡量网络关联度时存在着较大的差异。

2.关联度指标的相互比较

前文的分析已初步说明几个网络关联度指标间存在着差异，本部分通过相关性分析及格兰杰因果检验详细比较指标间的领先滞后关系。表3 报告了相关研究结果，其中Panel A 是相关性分析结果，下三角为Pearson相关系数，上三角为Spearman 秩相关系数，Panel B 是滞后4阶的格兰杰因果检验。从Panel A 可以看到，DCI 与DCI_Vol 之间的Pearson 和Spearman 相关系数分别达到0.6 和0.62，Spillover 和Spillover_Vol 间的Pearson 和Spearman 相关系数分别达到0.89和0.90，说明基于收益率和基于波动率计算的网络关联度差异较小。但是DCI和Spillover间的相关系数较小，其相关系数均在0.18以下。从Panel B可以看到，DCI是其他三个指标的格兰杰原因，Spillover 仅是Spillover_Vol 的格兰杰原因，DCI_Vol 是DCI 和Spillover 的格兰杰原因，Spillover_Vol 不是任何指标的格兰杰原因。因此综合来看，DCI 和Spillover 虽然度量的都是网络关联度，但是传递出的信息存在着较大的差异，基于收益率的DCI和Spillover 相对于基于波动率的DCI_Vol 和Spill_Vol 具有更多的信息含量，DCI在度量网络关联度时的信息含量最高。

表3 相关性分析及格兰杰因果检验

3.基于格兰杰因果网络的行业特性分析

基于前文的分析，DCI在度量行业网络关联性时具有较高的信息含量，且式（3）为分析各行业在信息溢出中的地位提供了可行性，因此本部分采用格兰杰因果网络来详细探讨各行业在DCI 指数较高时的信息溢出特性。图2 绘制了几个特殊时点的格兰杰因果网络，其中右边三个小图为DCI较高的三个极端点时的网络图，包括2007年5月、2012年12月21日和2015年6月26 日。其中2007 年5 月30 日 和2015 年6 月26日代表着两次股灾，此时市场具有极高的下跌风险，2012 年12 月21 日也是一个反弹的小高点，在随后一段时间股市也发生了小幅下挫。作为对比，左边三个小图展示了对应的3 个DCI值较低时间点的因果网络，包括2005 年8 月12日、2011年11月25日和2014年5月30日。图中节点代表各个行业，节点间的连线代表行业间存在着因果关系，箭头代表因果关系的方向，每张图中都标出了3个较大的节点，代表着3个具有最多对外因果关系的行业，即信息溢出最多的行业。

可以看到，相对于右图DCI较高时点的网络图，左图DCI 较低时点的网络图中的连线很少，如2005 年8 月12 日仅存在着4 个因果关系，而在市场下跌风险较大时，格兰杰因果网络变得更为复杂，图形中布满了连线，表明行业间的信息溢出变得更多更充分。这也在一定程度上反映了当行业间的联动变得越来越紧密时，市场系统性的下跌风险也会越大。从信息溢出的行业看，在市场下跌风险较大时，食品饮料（2007年）、采掘（2007 年）、通信（2007 年）、医药生物（2012 和2015 年）、有色金属（2012 年）、公用事业（2015年）和传媒行业（2015年）更容易成为风险溢出源。

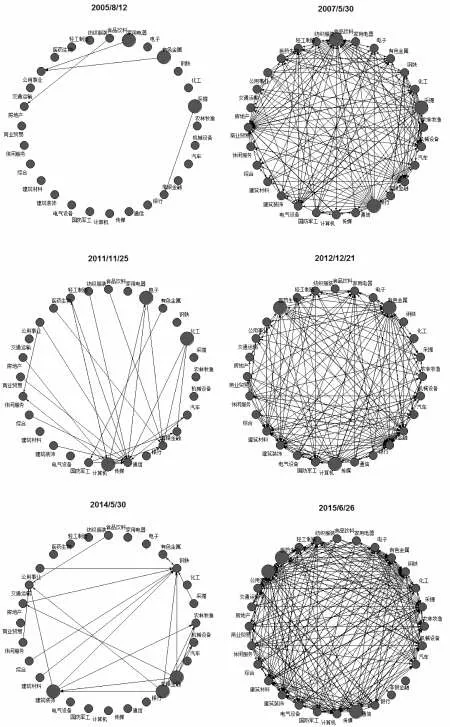
图2 行业间格兰杰因果网络图

图2报告了3个DCI较高时间点的风险溢出情况，属于点估计，并不能很好的将DCI 较高时间的全貌反映出来，因此表4列示了DCI最高的40个时间点下各行业的风险溢出情况。具体方法为：计算DCI 最高的40 个时间点下每个行业的对外信息溢出数（即对外格兰杰因果检验的显著数量）以及接受信息溢出数，再筛选出对外溢出数最高的5 个行业以及接受信息溢出数最高的5 个行业，最后统计每个行业在“最高5 个行业”中出现的频数。表4 中Panel A 报告了各行业出现在对外溢出“最高5个行业”中的频数，Panel B报告了各行业出现在接受溢出“最高5个行业”中的频数。可以看到与图2略有差异的结果，钢铁行业的对外溢出频次最高，达到了25次，说明有62.5%DCI较高的时间点，钢铁行业更容易将自身风险向外溢出。从Panel B接受溢出数可以看到，钢铁行业受外部风险传染的影响也很大，其接受溢出频数同样达到了25，计算机和有色金属行业紧随其后。钢铁行业属于典型的周期性行业，尤其是我国目前的经济发展模式较大程度上仍然对固定资产投资有较强依赖，当经济状况出现一定变动时，钢铁行业的利润就会出现较大波动，进而带来股价波动加剧，因此其对外溢出及接受溢出数最多。

表4 DCI高点时各行业的风险溢出频数

由于对外溢出较高的行业很可能也是接受溢出较高的行业，因此单独看对外溢出值可能并不能对行业在风险传染中的地位进行判断，采用净溢出频数（对外溢出频数减去接受溢出频数）效果会更好。图3报告了各行业的净风险溢出频数，可以看到，医药行业的净溢出频数最高，达到了18，紧随其后的是休闲服务、采掘及食品饮料，而有色金属行业的净溢出频数最低，为-14。因此综合来看，医药生物行业在股市下跌风险较大时对外影响更大，而有色金属行业在股市下跌风险较大时更容易受系统风险的影响，也就是说，相对于其他行业，这两个行业在股市下跌风险较大时的系统重要性较高。医药生物属于大消费行业，在我国人口老龄化的大背景下，行业指数一直保持较为稳定的上涨趋势，从表1 可以看出，其夏普比率仅次于食品饮料行业，该行业具有一定的独立性，其他行业对其影响较小，接受溢出数较少。而之所以对外溢出数较多，可能原因在于DCI高点往往是股价上涨到阶段性顶点的时候，医药行业由于具有较强的创新及科技属性（如在创业板指中医药行业的权重接近30%），股价涨幅及波动往往更大（如2015年上半年医药行业涨幅达到80%，仅次于电子、计算机等科技属性更强的行业），从数据上看，在高点时风险容易向其他行业扩散。有色金属行业属于顺周期的上游原材料行业，其股价波动较大（仅略低于非银金融和军工行业），且更容易受到下游需求行业的影响，从而导致其被溢出程度较高，但是对其他行业的影响却并不是很高，从而导致其净溢出度最低。表4 和图3 中虽然包含了40 个DCI 最高时的行业溢出情况，但仍属于小样本估计，这两个行业是否能够对股市下跌风险进行预警和判断，还需要采用全样本数据进行估计和分析。

图3 各行业净风险溢出频数

（三）网络关联度对股市下跌风险的影响

1.系统网络关联度的影响分析

表5 系统网络关联度对下跌风险的影响

采用系统网络关联度DCI 和Spillover 研究其对股市下跌风险的影响，结果如表5所示。其中Panel A是直接对下期指数收益率的OLS回归结果，Panel B 是对下跌风险的Logit 回归结果。模型（1）（2）（3）是采用DCI回归的结果，模型（4）（5）（6）是采用Spillover回归的结果。模型（2）和（5）是考虑了牛熊市的影响，模型（3）（6）是考虑了投资者情绪的影响。从Panel A的结果可以看到，无论是采用DCI还是Spillover 均对指数的下期收益率无显著影响，且无论是采用牛熊市还是投资者情绪划分样本，研究结论均是一致的，说明用网络关联度来直接对股市收益率进行预测是无效的。Panel B 的结果则说明，系统网络关联度能够对股市的下跌风险进行较好的预测，DCI 和Spillover 的系数均显著为正，说明网络关联度越高，股市的下跌风险越大。且Spillover的预测效果更好，这无论是从系数绝对值大小、T 检验值大小，还是R2值均可以看出。考虑了牛熊市划分后发现，由于Net×Market 的系数均显著为正，说明DCI和Spillover均在牛市时的预测效果更好，而DCI在熊市时几乎没有预测能力。考虑了投资者情绪后发现，DCI的预测能力主要表现在低情绪期，在高情绪期的预测作用小很多，Spillover 对情绪并不敏感，高情绪期的预测能力比低情绪期略强。综合来看，系统网络关联度对股市下跌风险具有一定的预测能力，且预测能力会受到牛熊市和投资者情绪的影响。

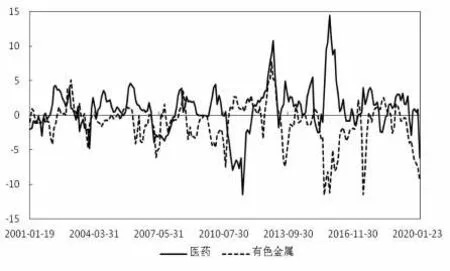
图4 医药和有色金属行业净溢出度曲线

2.基于行业净溢出度的分析

医药行业和有色金属行业分别是净溢出度最大和最小的两个行业，因此本部分采用这两个行业的净溢出度作为网络关联度的替代变量，研究特定行业净溢出度对股市下跌风险的影响。图4 报告了两个行业净溢出度在样本区间的走势图，可以看到两个行业净溢出度存在着一定的负相关性，经计算两者相关系数为-0.2，说明两者不光在DCI较高时存在着负向关系，在整个样本区间这种负向相关性也是存在的。

表6报告了行业净溢出度的回归结果，净溢出度指标与网络关联度一样，对数差分取变化率。其中Panel A是医药行业净溢出度的研究结果，Panel B 是有色金属行业净溢出度的研究结果。模型（1）（2）（3）是OLS 回归结果，模型（4）（5）（6）是Logit 模型的回归结果。可以看到，医药行业净溢出度只有在高情绪期才对股市下跌风险有预测作用，而有色金属行业净溢出度在全样本、牛市期以及高低情绪期都能够对股市下跌风险有预测作用，由于在网络关联度最高时，有色金属行业净溢出度最小，因此有色金属行业净溢出度的回归系数为负。综合来看，医药行业净溢出度对股市下跌风险的预测作用不明显，但有色金属行业净溢出度却对股市下跌风险有显著的预测作用，且在进行了牛熊市或投资者情绪划分后，预测作用仍然是显著的。这很可能是因为，医药行业虽然净溢出度很高，但是实际从行业属性看，该行业具有较强的特殊性及独立性，与其他行业的关联性较弱，因此用其来进行股市整体分析时，效果并不好。但是有色金属行业属于典型的顺周期行业，其与经济周期的关联程度非常高，如铜价往往被视为宏观经济周期的先行指标，与其他行业的关联性更强，因此用其来对股市整体进行分析时，能够具有较好的效果。综合来看，表4和图3利用DCI高点时的小样本估计，观察到医药行业和有色金属行业在系统风险较大时的系统重要性更高。但是从全样本看，无论是基本面逻辑还是数据分析结果，有色金属行业对于判断股市的整体下跌风险更为有效。

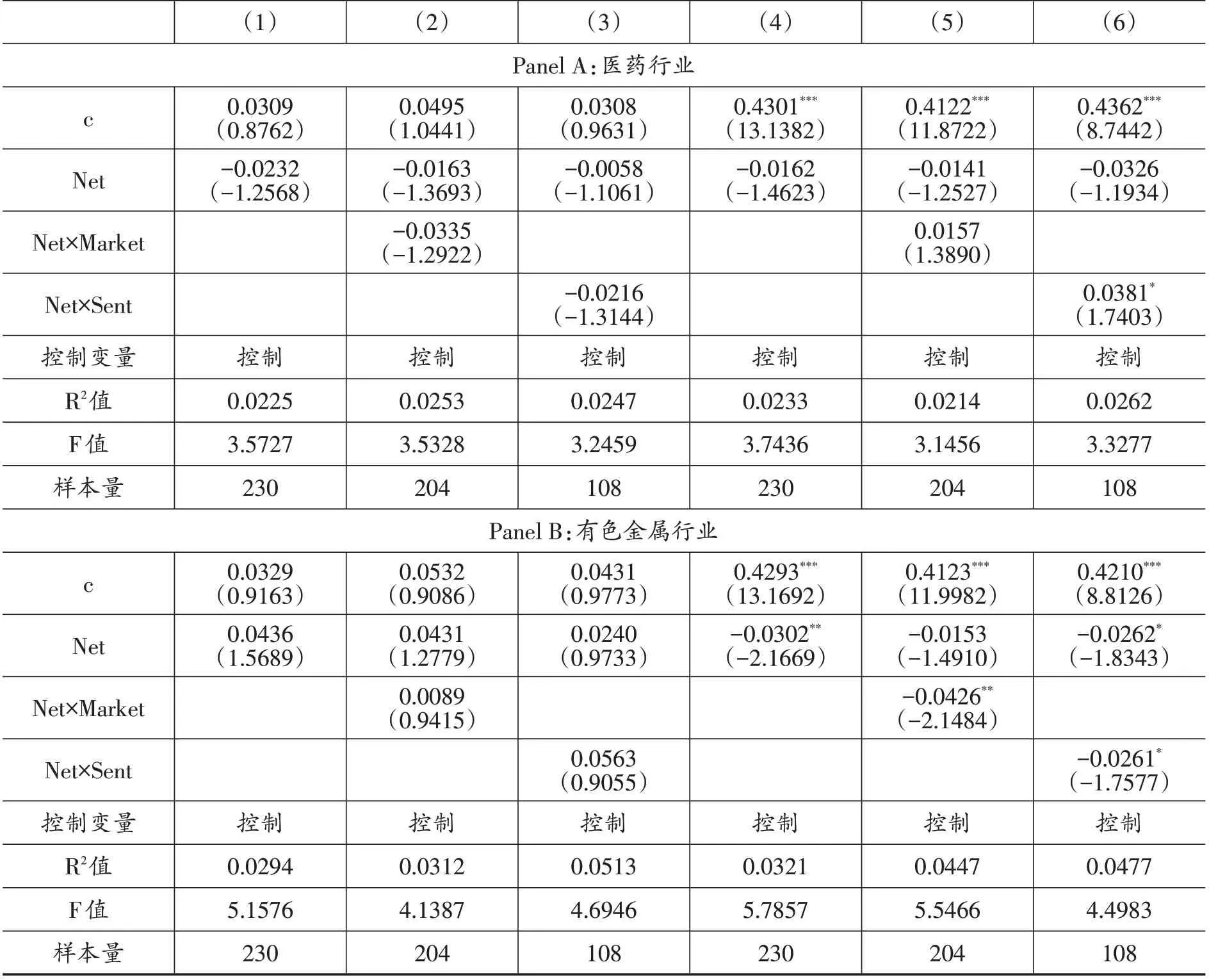
表6 基于医药和有色金属行业净溢出度的研究

3.稳健性检验①限于篇幅，检验结果留存备索。

本部分对前文研究结论的稳健性进行检验，首先将样本拆分为2001—2010年和2011—2020年两个阶段，由于投资者情绪仅在2011 年后有数据，因此分阶段检验仅对网络关联度整体以及按照牛熊市划分的研究结果进行了检验，投资者情绪的分样本检验不考虑在内。结果与前文的研究结论基本类似。针对Logit指标的设定标准，首先将Logit 阈值设定为-5.3%，即当下月股市收益率小于-5.3%时，Logit为1，反之则Logit 为0。接着将Logit 阈值设定为-8.6%，回归结果显示前文的研究结论是稳健的。

五、研究结论

本文利用格兰杰因果网络模型（DCI）和信息溢出模型（Spillover）测度了我国股市的行业网络关联度，通过分析网络关联度动态变化特征及各个行业对外风险净溢出，并考察网络关联度对股市下跌风险的影响。主要得出以下结论：第一，行业网络关联度可以较好地对股市的系统风险进行度量，在股市泡沫较高时期（如2007年和2015年）网络关联度大幅提升，往往预示着泡沫的不断累积。第二，行业网络的深层分析可以有效识别出各行业在风险传导过程中的地位和作用，如医药和有色金属行业在股市下跌风险较大时的系统重要性会高于其他行业。第三，网络关联度对于股市下跌风险具有一定的预测能力，市场状态或投资者情绪会对预测能力产生一定影响，部分特殊行业如有色金属业由于在网络中的地位较高，因此其净溢出度同样可以作为股市下跌风险的预警指标。

本文的研究结论对于金融投资实践的风险控制有着较强的经验价值：第一，由于所有的行业或股票都面临着市场风险，因此经常表现出同涨同跌的特性，但是这种网络关联度却不是稳定不变的，而是随着市场环境的变化而时刻变化着的，尤其是在网络关联度较高时，往往预示着较高的股市下跌风险，因此对网络关联度的有效识别可以为风险控制提供理论依据。第二，不同行业在系统风险传导中的地位并不相同，如医药行业在网络关联度较高时往往属于风险溢出的角色，但是有色金属行业则属于接受风险溢出的角色，因此在进行金融投资实践时，应考虑不同行业间的异同，包括可以采用类似于美林投资时钟等工具在行业间进行轮动，从而进一步规避市场的下跌风险。第三，不同股票和不同行业间的收益率往往关联度较高，如Spillover 在样本区间均在80 以上，因此要想进一步实现对风险的控制，除了要关注行业间的联动和轮动，可以同时考虑如商品、债券等其他类别的资产，通过组合投资的方式实现风险的分散。