金属增材制造负载均衡异构并行切片算法
2021-05-19李慧贤马创新
李慧贤 马创新 王 硕 马 良
1.西北工业大学计算机学院,西安,7100722.西北工业大学软件学院,西安,7100723.西北工业大学凝固技术国家重点实验室,西安,710072
0 引言
金属增材制造(metal additive manufacturing)技术作为一种新兴制造技术,相比传统制造工艺,其成本低、材料利用率高,被广泛应用于航空航天、仪器仪表等领域[1-2]。切片算法是增材制造数据处理过程中非常重要的一步,对于一个3D模型,首先要做的便是将三维模型分成一系列二维平面,得到切片轮廓后便可将三维加工转为二维加工。
现在金属增材制造的发展日新月异,随着打印规模的增大和精度要求的提高,切片算法的数据量也越来越大。目前大多数切片软件都采用串行切片算法,研究如何提高切片算法的效率是很有必要的。增材制造领域的分层切片算法主要分为以下三类:基于面片拓扑关系的分层切片算法[3-5]、基于模型几何特征的分层切片算法[6]、基于几何连续性的分层切片算法[7]。在并行化切片算法研究方向有很多报道。马旭龙等[8]提出了基于共享存储并行编程(open multi-processing,OpenMP)的快速并行分层算法,利用CPU多核心建立数据并行模式。马旭龙等[9]提出了基于流水线的并行分层算法,进一步提高并行效率,可获得接近CPU核数的加速比。然而CPU更擅长逻辑运算而非数值计算,且CPU核数有限,限制了并行效率的提高。现在基于 GPU并行计算的研究范围越来越大,各个通用计算领域都开始尝试使用统一计算设备架构(compute unified device architecture,CUDA)进行GPU加速[10-13]。在增材制造技术方面,ZHANG 等[14]、王硕[15]利用CUDA将传统切片算法并行化实现,切片效率提高明显,而且数据量越大该算法越具优势。但是该算法逻辑判断较多,且未考虑负载均衡,限制了GPU性能。本文提出了在金属增材制造中基于模拟退火的负载均衡异构并行化算法,并行处理STL模型切片时的求交问题,以提高后续求取轮廓线的效率。
1 并行化异构切片算法
1.1 数据结构的构建
为了更好地将切片算法并行化,本文在基于面片间拓扑关系的半边数据结构的基础上提出了一种改进的数据结构模型。半边数据结构如图1所示。
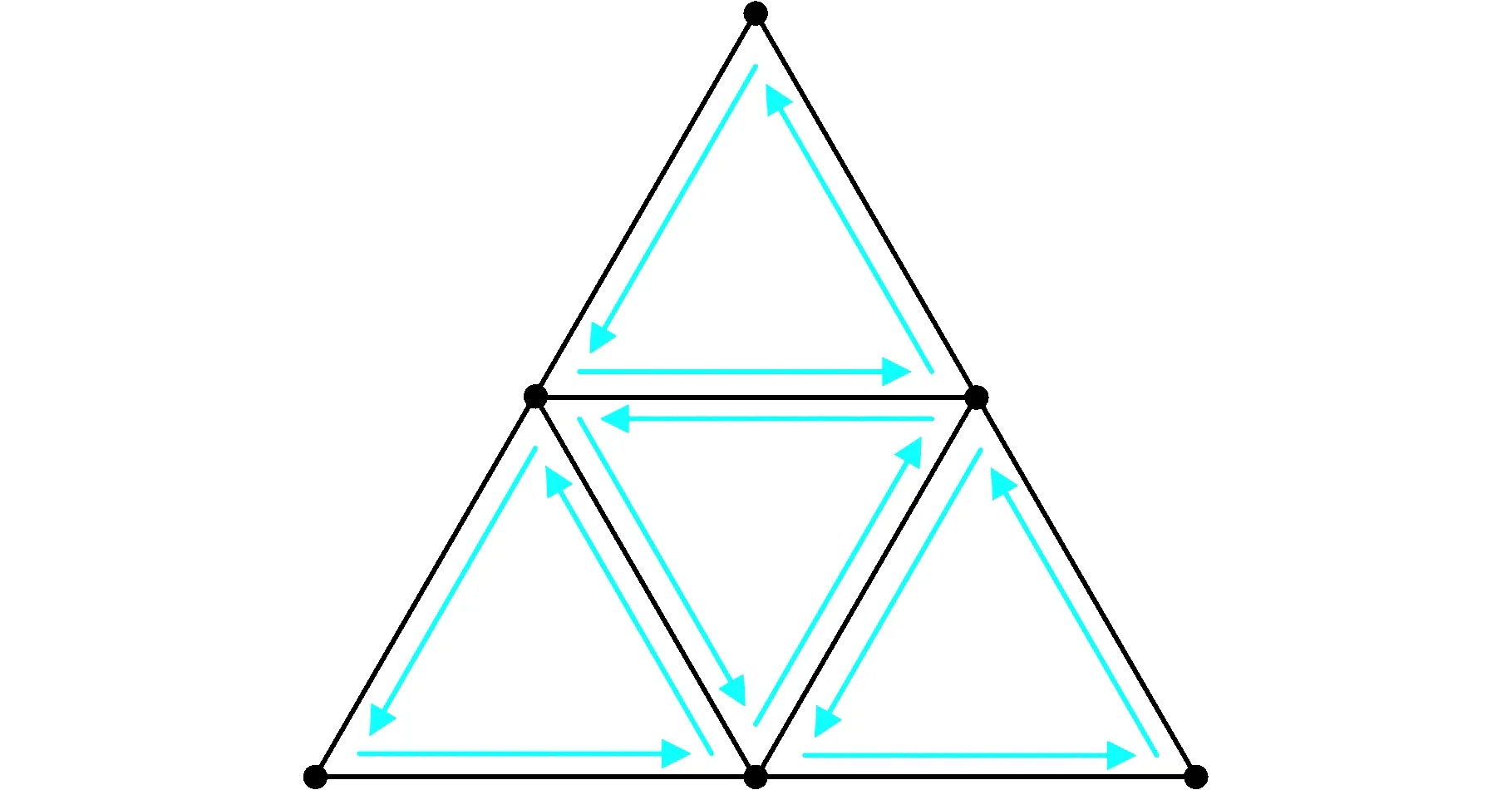
图1 半边数据结构Fig.1 Half-edge data structure
根据格式(ASCII码/二进制)读取STL文件,在得到该零件模型所有三角面片的同时,也得到该模型的最低点。然后遍历所有三角面片,利用面片间的拓扑关系建立数据结构。首先遍历所有三角面片的每个顶点,对每个点的坐标值用哈希函数计算哈希值,然后比对哈希表中是否有该点,若有则使用哈希表中的索引,否则存入哈希表并使用哈希表中的索引代替该点。这样既可以去除相邻三角面片之间重复记录的共用顶点,也可以利用这些三角面片间的共用顶点将相邻的三角面片联系起来形成拓扑关系,从而构建基于拓扑关系的数据结构。该零件模型可用点集和面片集合来表示,点集存储模型中出现的所有点,面片集合中每个面片的顶点则由点集中的索引代替。
在建立该数据结构的同时,为了利于后续并行化切片的流程,记录每个三角面片在Z轴的最低点Zmin及最高点Zmax,并根据开始记录的零件模型最低点以及切片层高δthickness,计算得知该三角面片会被哪些层高的切平面切到,以便在并行化切片前统计任务量并分配任务。
1.2 数据预处理
三角面片通常会与多个切平面相交(图2),数据结构构建完成后,遍历其面片集合,根据上一步计算结果将三角面片加入所有相交切平面的求交三角面片集合中。
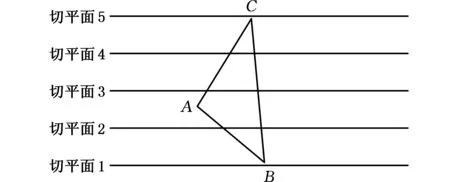
图2 三角面片的多个相交切平面Fig.2 Multiple intersecting tangent planes oftriangular patches
为了减少数据在内存和GPU间的频繁交换,CUDA平台采取了一次复制进、一次复制出的策略,当某些线程任务量差距巨大时,先完成计算的线程需要等待未完成的线程,整个任务的运算时间取决于运算时间最长的线程。所以在并行计算问题中,对任务量的负载均衡是提高算法效率的关键,也是研究的重点。本算法根据线程数分配给每个线程尽量相等的任务量,以减少线程等待时间。该问题可以类似为一个装箱问题,尽可能提高装箱填充率,便能使各线程工作量更加均衡。
本文提出的并行化切片算法首先根据任务量和硬件设备确定所需要开辟的线程数N,并根据所有切平面求交集合的累加和得到总任务量P及每个线程的理想任务量Pthread:
Pthread=P/N
(1)
即每个箱子的容量。每个切片层求交集合的长度即为需要装入箱子的物体的长度,这是一个单维装箱问题。装箱问题通常带有大量的局部极值点,很难得到最优解,反而会在循环过程中陷入局部最优解,模拟退火算法是求解这类问题的通用方法。
该问题与传统装箱问题的区别在于可以对每个切片层求交集合进行分割,若某个切片层求交集合过大,则可以切分给多个线程进行运算,但是这种操作会增加运算负担,应尽量避免。如果第i个切片层求交集合的长度Player[i]大于(1+5%)Pthread时,则对该层任务量进行分割,Player[i]的任务量分割成Pthread的整数倍后剩余的部分则是需要装箱的部分。算法1具体流程如下。

Algorithm 1任务分割算法Definition1 Pthread=理想的每个线程所需分配任务量;2 PlayerSize=每层任务量3 Pdone=无需重新组合的分割结果集合4 Predo=需要重新组合的分割结果集合5 Mdone=对Pdone的每一项标记,表明其来自哪个切平面的集合6 Mredo=对Predo的每一项标记,表明其来自哪个切平面的集合7 Layers[i] = =每层面片集合8 i=09 Repeat i++10 If PlayerSize[i]>(1.05Pthread); 11 j=0;12 Repeat13 (Layers[i][j],Layers[i][j+Pthread-1])部分集合赋值Ltemp;14 Pdone.push_back(Ltemp);15 Mdone.push_back(Mark(i,Ltemp.size())); 16 j+=Pthread17 until j>PlayerSize[i]18 (Layers[i][j-Pthread],Layers[i][PlayerSize[i]-1])部分集合赋值Ltemp;19 Predo.push_back(Ltemp):20 Mredo.push_back(Mark(i,Ltemp.size()));21 Else if PlayerSize[i]<(0.95Pthread);22 Predo.push_back(Layers[i])23 Mredo.push_back(Mark(i,Ltemp.size()))24 Else25 Pdone.push_back(Layers[i])26 Mdone.push_back(Mark(i,Ltemp.size()))27 until i=PlayerSize.size()28 EndAlgorithm 1
1.3 基于模拟退火的负载均衡算法
模拟退火算法的实质是根据Metropolis准则[16]用概率P来接受更差的结果, 即
(2)
其中,E(·)为评估函数,xnew为新解,xold为原解。P随着温度的下降而下降,最后趋于稳定,得到一个近似最优解。本文的问题和原有装箱问题有所区别,箱子的长度可以在(1±5%)Pthread之间浮动,以尽量减少运算负担。在得到需要分配给各个线程的切片层求交三角面片集合长度的集合Predo之后,便可以利用下述算法将Predo重新分配,使每个线程的任务量接近(1±5%)Pthread。
首先利用贪心算法[17]中的首次适应法进行第一次装箱,得到初始解。然后随机交换物体的排列顺序,再次使用贪心算法放入得到新解,得到新解后,计算利用率和原解比较,若更好则接受新解,若更差则以一定概率P来接受较差解。循环重复此过程,每次循环温度降低,直到温度为0,状态趋于稳定。算法2具体流程如下。

Algorithm 2负载均衡算法Definition1 Predo=需要重新组合的分割结果集合;2 Ptemp=临时保存集合;3 Mredo=保存的Predo中每一项所处切平面的标记集合;4 Mtemp=临时保存标记集合;5 S=当前解6 S'=新解7 T=初始温度;8 r=退火速度;9 Tmin=最低温度;10 times=迭代次数;11 FF(vector
1.4 CUDA并行化切片
使用自适应负载均衡算法得到每个线程所需计算的任务集合后,将任务集合利用CUDA传入GPU中进行并行化求交运算。前一过程求得的任务集合包含了每个线程所要计算的一个或多个求交三角面片集合以及每个求交三角面片集合的标记。求交三角面片集合的标记包括其切平面高度以及该切平面高度需要进行求交计算的次数。根据任务集合,将每一项中的面片集合及标记集合转换为一维数组,并按照此计算结果提前申请结果数组,用来保存计算结果,同时将保存的标记中记录的切平面高度赋值给每一项切片结果的Z值。传入GPU后,各个线程得到自己的存储位置下标,计算完成得到结果后依次存储,待所有线程都计算完成后将结果传回CPU。该部分算法在CUDA中运行的各线程内核函数如算法3所示。

Algorithm 3CUDA内核函数Deition1 i=线程索引;2 k=当前存储位置3 layersSize=切平面集合的个数4 Result=结果数组5 Index=索引数组6 i=threadIdx.x+blockIdx.x×blockDim.x7 If i≥layerSize; 8 EndAlgorithm 3;9 k=Index[i]10Repeat11 Result[k]=S[k]与Result[k].z的求交结果;12 k++ ;13until k=Index[i+1]14EndAlgorithm 3
由算法3可见,各线程的运算量和逻辑判断大大减少,所有线程计算完成后将计算结果传回主机端,再按照集合中保存的标记信息将计算结果恢复为按切平面高度存储的计算结果集合。得到每一层切平面与该层相交的所有三角面片的相交线段的计算结果后,即可按照每层与切平面相交的三角面片间的拓扑关系,快速寻找各个相交线段的相邻线段,从而连接成切片轮廓。至此本文研究的自适应负载均衡异构并行切片算法全部完成。
2 实验结果
2.1 实验数据与环境
实验环境:操作系统Win10 64位,处理器Intel Core i7-8750H,内存16G,显卡NVIDIA GTX 1050 Ti with Max-Q Design,CUDA版本8.0,编程平台Visual Studio 2015。本次实验所用的STL文件来源于网络,文件大小100~750MB。
2.2 实验内容
2.2.1模拟退火算法参数实验
模拟退火算法的运算效率和准确性由初始温度、退火速度等参数决定,为得到最适合的参数,首先对该自适应负载均衡算法中的这两组参数进行对比实验。修改参数值,将各个模型使用1.2节所述的数据预处理算法处理后得到其Predo集合,记录填充率、耗时及迭代次数等,其中参数初始温度T的对比实验结果见表1,该实验中退火速度r设为固定值0.9。退火速度r的对比实验结果见表2,该实验初始温度T设为固定值200。
由上述对比实验可以得出,退火速度和初始温度的改变会对算法用时产生比较大的影响。当模型数据非常巨大时,所要处理的计算量很大,对任务分配的优化很有意义,可以牺牲自适应负载均衡算法的运算时间来提高切片过程的运行效率,所以应该升高初始温度,降低退火速度,使得算法更大概率地计算出近似最优解;当模型数据量较小时,可适当降低初始温度,提高退火速度。
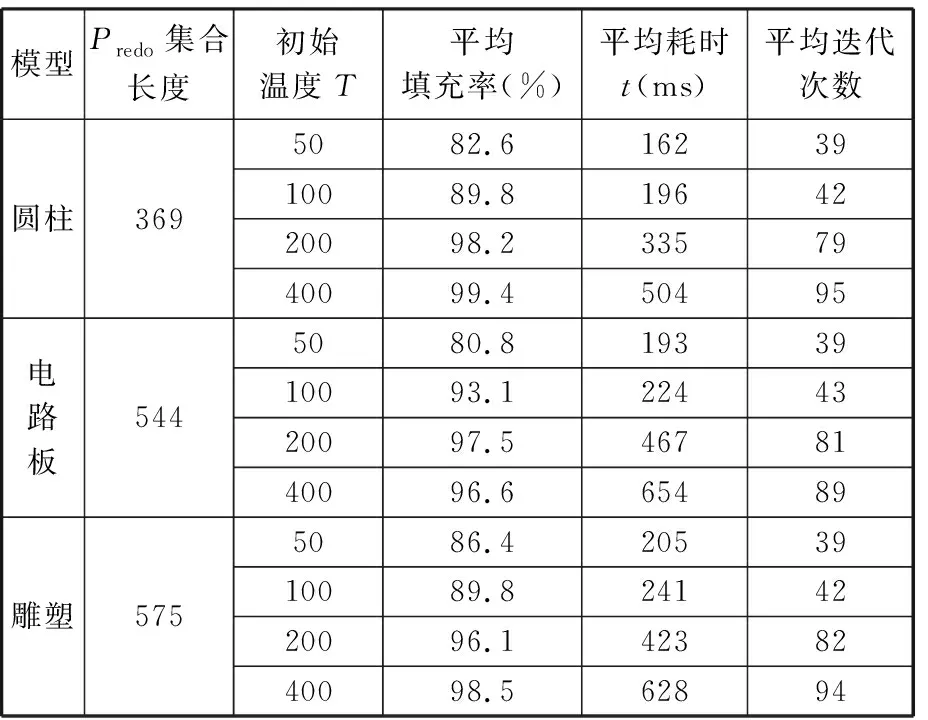
表1 模拟退火算法处理不同模型时初始温度的对比

表2 模拟退火算法处理不同模型时退火速度的对比
2.2.2算法对比实验
本节对比实验中所要对比的算法有以下4种:①基于面片间拓扑关系的串行算法;②基于CUDA的普通切片算法;③基于拓扑关系的GPU并行切片算法;④自适应负载均衡异构切片算法。首先对其求交过程进行对比测试,实验结果见表3。由表3可以看出,本文算法在单纯的求交运算方面由于传入数据含有多个变量且数据结构较为复杂,计算速度慢于算法②,因为算法②单纯计算求交结果,不含拓扑结构;在处理模型1、2、4时,算法④所耗时间短于算法③,是因为模型1、2、4结构较为复杂,算法③中没有对这些模型进行优化,而算法④缩短了线程等待时间,加快了切片速度。
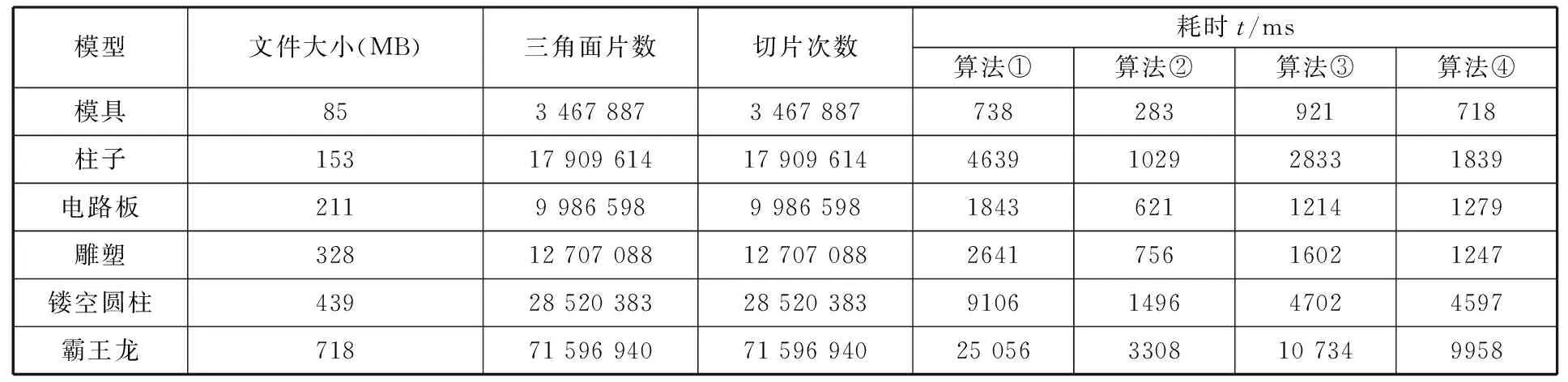
表3 不同切片算法对不同模型的求交过程耗时对比
对4种算法的整体分层切片过程进行测试,耗时对比如图3所示。可以看出,各算法耗时随模型体积增加都呈线性递增趋势。普通并行切片算法耗时最多,这是由于轮廓形成过程需要进行大量的数组遍历操作。三角面片间的拓扑关系有利于快速寻找各个相交线段的相邻线段,从而连接成切片轮廓,因此,基于面片间拓扑关系的串行算法效率提升较大。
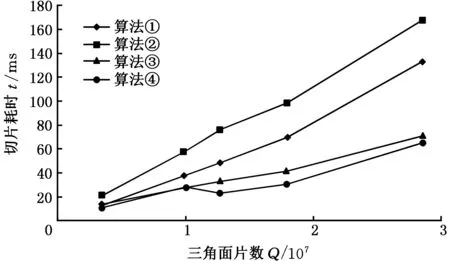
图3 不同切片算法处理不同模型耗时对比Fig.3 Time consuming comparison of different slicingalgorithms for different models
算法③和算法④将求交部分并行化,相比算法①,加速比达到3左右。对比算法③,在处理不规则模型(图4a)时,由于模型曲率变化明显,不同切片层间的运算量差异很大,算法④效果较好,它会消耗少量的时间来换取后面切片时不同进程间的负载均衡,在CUDA中并行求交的过程效率可再提高20%~30%。图4b所示是采用本文算法获得的切片结果,本文算法能正确地利用STL模型进行分层切片。
3 结 论

(a)霸王龙STL模型

(b)霸王龙切片数据图4 模型切片实例Fig.4 Model slice example
本文提出了自适应负载均衡异构切片算法,采用模拟退火算法来解决任务重组问题,将并行计算时所有线程的任务总量尽量平均分配给每个线程,使得每个线程所需计算的任务量差距在可接受范围内,避免线程等待等问题。在对不规则模型数据分层切片时可以得到较好的加速比,且实验模型体积越大,算法的加速比越明显。
