基于GABP和改进NSGA-Ⅱ的高速干切滚齿工艺参数多目标优化决策
2021-05-19刘艺繁阎春平倪恒欣
刘艺繁 阎春平 倪恒欣 牟 云
重庆大学机械传动国家重点实验室,重庆,400030
0 引言
高速干切滚齿加工是一种符合齿轮加工发展方向的加工技术,相比传统湿式滚齿加工,高速干切滚齿的加工效率明显提高,同时避免了切削液的使用,加工过程更加环保[1]。高速干切滚齿加工过程中,切削热量高且释放不均匀,工艺参数的调整会影响加工刀具与工件的受热分布情况,进而影响加工能耗、刀具寿命和加工质量[2],故需要研究高速干切滚齿加工过程中刀具寿命、加工效率、加工能耗、工件质量等与工艺参数之间的关系,在延长刀具寿命的同时,降低加工能耗、加工时间与加工成本,实现高速干切滚齿加工特性的最优化[3]。
目前国内外学者针对滚齿加工参数优化研究的主要目标包括加工时间、切削精度、切削振动、刀具寿命及加工成本等。KANE等[4]建立滚齿加工参数与加工成本的函数模型,对滚刀转速和进给量进行了优化。KARPUSCHEWSKI等[5]通过试验研究了加工参数对滚刀刀具磨损、刀具寿命的影响规律,并将其用于提高齿轮的加工精度,得到最优的滚刀转速和进给量范围。YANG等[6]分析切削热传递三阶段,以滚刀转速、进给量和空气流速等加工参数为变量,建立面向切削时间和切削热量的优化模型。SANT’ANNA等[7]构建了滚刀冲击频率与加工参数的优化函数模型,通过试验分析加工参数对滚齿切削振动的影响规律。SUN等[8]应用改进粒子群算法建立了滚齿加工工艺参数与齿轮几何偏差的关系模型,通过减小最小齿形几何误差来提高齿轮加工精度。
随着能源消耗问题日趋严峻,已有学者针对滚齿加工参数能耗优化问题进行了深入研究。CAI等[9]通过滚齿加工试验对滚齿切削时间和比能进行优化研究,发现在一定范围内提高切削转速能缩短切削时间和降低切削消耗。CAO等[10]通过试验研究建立滚齿加工成本和能耗的优化模型,提出一种蚁狮搜索算法对加工参数进行优化以降低切削能耗。LIU等[11]提出一种模糊自适应控制方法,通过加工试验实时优化改变滚刀轴向进给速率,使切削扭矩恒定来缩短加工时间和降低切削过程能耗。钟健等[12]提出一种基于实例推理的优化决策方法以降低滚齿切削能耗。
上述研究主要揭示加工参数对滚齿切削能耗的影响规律,针对特定的滚齿机床及加工环境下单个目标的工艺参数优化问题,通过实验研究获取最优参数或最优参数范围,从而构建加工参数与能耗的数值优化模型。随着机床产品性能迅速提升,包括高速干切滚齿机床在内的加工机床已成为主流加工机床。高速切削不仅需要更多能源消耗,同时对刀具的高速切削性能提出更为严苛的要求。一方面,高速切削时刀具的切削温度随之升高,若数控程序或切削参数设置不当,会造成刀尖温度快速上升,加工滚刀磨损严重,从而直接导致刀具寿命急剧下降;另一方面,滚刀切削寿命与工艺参数之间并不存在线性映射关系,研究滚刀切削寿命、加工能耗与加工参数的关系,构建较精确的综合优化模型是高速干切滚齿加工的必然发展方向,也是企业实际加工的迫切需求。
本文针对具体的高速干切滚齿工艺参数决策优化问题,基于第二代非支配排序遗传算法(nondominated sorting genetic algorithm Ⅱ,NSGA-Ⅱ)构建主体优化模型,以加工能耗最小、刀具寿命最大为优化目标,基于DBSCAN(density based spatial clustering of applications with noise)算法得到与滚齿工艺问题的加工条件相近的实际加工样本集,获取多目标优化模型输入区间,利用遗传-反向传播算法(genetic algorithm-back propagation, GABP)神经网络构建加工优化目标值的预测模型并作为适应度函数,迭代优化出与待优化滚齿工艺问题匹配的Pareto最优解。
1 高速干切滚齿工艺参数优化问题的总体分析
1.1 问题描述
将待优化工艺问题记为U=(R0,P0,R,P,OP,S),其中,R={r1,r2,…}记为加工条件集,P={p1,p2,…}记为加工工艺参数集,OP={W1,T1;W2,T2;…}记为优化目标集,S={s1,s2,…}记为约束参数集,R0、P0分别为滚齿工艺问题的加工条件与加工工艺参数,Ti为刀具寿命,Wi为加工能耗,si为每一个工艺样本中的约束参数集。
1.2 优化变量
在工艺参数决策中,不仅需要确定切削深度、进给量和切削速度,为了精确优化加工能耗与滚刀寿命,还需要确定滚刀头数、轴向进给速度、主轴转速等参数。由于切削深度对机床床身、滚刀、工件变形影响小,不足以影响滚刀切削寿命,故不考虑将切削深度作为优化变量;而在车间实际加工过程中,由于机床性能的提高,为了提高生产效率,通常采用最大切削深度和进给量进行滚齿粗加工,故不考虑将进给量作为优化变量。切削速度、滚刀头数、轴向进给速度、主轴转速对加工优化目标影响较为明显,因此,将滚刀头数、切削速度、滚刀转速、轴向进给速度确定为优化变量。
1.3 优化适应度函数
本文主要从加工能耗和刀具寿命两个方向进行优化,将适应度函数记为
F(ri,pi)=QWT
(1)
其中,QWT为由能耗值与刀具寿命值组成的二维矩阵。通过输入具体的加工条件与工艺参数,得到预测的加工能耗与刀具寿命,从而支持优化模型进一步筛选迭代。ri由加工条件下参数具体值组成,见表1;pi由具体优化变量值组成,见表2。
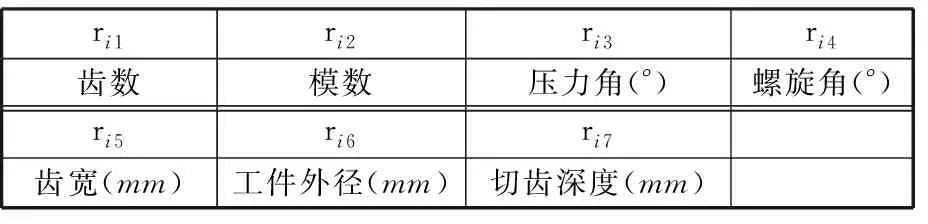
表1 加工条件

表2 优化变量
1.4 约束条件
高速干切滚齿机床工艺参数的选择,是在机床自身性能和保证滚齿机床加工零部件质量等前提条件下进行的[13],需要满足包括滚刀主轴转速、轴向进给速度、切削速度、加工质量、加工时间、机床性能等多种约束条件。由于相似加工样本集内样本与滚齿工艺问题的加工条件具有较理想的匹配度,在同一滚齿机床与场地条件下,机床性能相同,故本文排除机床性能不同产生的影响;工艺样本集是基于同一类型滚刀加工的数据,因此不考虑刀具类型不同所产生的影响;本文中滚刀主轴转速、轴向进给速度、切削速度等作为输入变量并通过DBSCAN算法获取取值区间,因此不作为约束条件。本文将加工质量和加工时间作为优化模型的约束条件。
2 基于GABP神经网络和改进NSGA-Ⅱ算法的多目标优化模型构建
2.1 多目标优化模型概述
本文基于改进NSGA-Ⅱ算法构建优化模型,通过聚类算法从工艺样本集中获取输入输出约束,以基于GABP神经网络构建的预测模型作为适应度函数,不断生成并迭代更新工艺参数集,最终输出Pareto最优解。
2.2 GABP神经网络预测模型的生成
反向传播(BP)神经网络作为一种具有连续传递函数的多层前馈人工神经网络,广泛应用于预测与分类领域,其缺点在于:隐含层神经元个数仍然没有标准的选取规则;在训练神经网络的过程中,若使用随机生成的原始网络结构,易于产生局部最优解,进而影响精度。GABP神经网络作为一种基于遗传算法(GA)改进的神经网络,利用遗传算法的全局寻优能力强、收敛效率高的特性,对神经网络的原始结构参数进行编码与迭代优化,能够有效改进传统BP神经网络的不足之处,进而提高预测的准确性。

(2)
式中,K为样本数目。
为了消除不同输入项的量纲影响,对样本值进行归一化处理:
(3)
式中,d、d′分别为转换前后的值;dmin、dmax分别为样本值转换前的最小值、最大值,处理后数值区间为[0,1]。
GABP算法优化神经网络结构参数的个体由以下4部分组成:OF与LF连接权值、LF阈值、LF与IF连接权值、IF阈值,将这些数值进行10位二进制编码,连接起来作为一个个体编码。为降低BP神经网络预测误差,选择预测样本的输出值与期望值的误差范数式作为适应度函数的输出,即
(4)
式中,xi为预测能耗和刀具寿命与其实际值之差;X为由xi组成的一维矩阵。
面向高速干切滚齿加工效果预测的GABP算法主要流程如下:基于神经网络结构生成初始种群,考虑到控制个体长度和个体数据项的精度,需要为个体进行二进制编码,将每次BP神经网络训练的输出误差的范数输出作为遗传算法的适应度函数值,经遗传算法产生新一代种群后,再次进行神经网络解码训练,最终得到最优的神经网络原始结构参数,见图1。面向高速干切滚齿加工效果预测的GABP算法主要步骤如下:①基于神经网络结构生成初始种群;②针对当前种群,考虑到控制个体长度和个体数据项的精度,需要为每个个体进行二进制编码,将当前种群个体作为神经网络结构参数进行训练,每次BP神经网络训练的输出误差的范数输出作为遗传算法的适应度函数值;③根据适应度函数值进行交叉、变异,产生新一代种群后,若不满足终止条件则返回步骤②再次进行神经网络训练;否则转下一步骤;④解码当前种群个体后,最终得到最优的神经网络原始结构参数。

图1 面向高速干切滚齿加工效果预测的GABP神经网络结构Fig.1 GABP neural network structure for predictionof high speed dry hobbing results
2.3 相似加工样本集的生成
通过改进NSGA-Ⅱ算法迭代寻找最优的工艺参数时,首先需要确定生成新个体工艺参数的取值区间。本文基于滚齿加工样本集,寻找与待决策滚齿工艺问题相似度较高的样本集,将相似样本集中的各项工艺参数上下限值作为NSGA-Ⅱ算法生成新个体的工艺参数取值区间,因此,需要一种聚类算法完成相似工艺样本集的获取。
DBSCAN算法是一种常用于非连续数据集的聚类算法,具有较强的筛噪能力、主动聚类能力和搜索能力,其主要思想如下:向当前某个对象簇中不断添加距离小于某个值E、包含对象数不小于某个阈值mpts的对象,直到不存在符合条件的对象,再对其他对象进行相同的递归操作,从而对该对象簇进行扩展。
本文的多目标优化模型需要从工艺样本集中抽取待优化滚齿工艺问题的相似加工样本集,进而确定优化模型的输入区间,DBSCAN算法对滚齿工艺样本的零散数据能够较好地进行识别并分类,故以DBSCAN聚类算法作为相似加工工艺样本集的抽取算法。基于DBSCAN算法的滚齿相似加工工艺样本集抽取方法的相关定义如下:
定义1Ti邻域的公式化定义为
NE(ti)={tj∈T|Tdist(ti,tj)≤E}
(5)
式中,E为工艺样本数据集的密度半径;T为给定的加工条件集与工艺参数集的并集;ti={ri,pi},ti的邻域由所有与其距离Tdist不超过E的工艺样本集构成。
定义2 任意两个工艺样本的距离Tdist(ti,tj)定义为
Tdist(ti,tj)=
(6)
式中,ti1~tik、tj1~tjk分别为ti、tj的k个加工条件项。
定义3 对于ti∈T,如果ti的邻域满足
COUNT(NE(ti))≥mpts
(7)
则ti为核心加工条件,如果同时满足
ti∈NE(ti)
(8)
式中,COUNT表示计算邻域元素个数;mpts为邻域密度阈值。
则ti到tj是直接密度可达。 式(8)表示加工条件tj在ti的E邻域范围。
定义4 在加工条件集R内,对于任意样本ti、tj、tk,若满足ti到tj是直接密度可达的,且tj到ti是直接密度可达的,则称ti到tk是密度可达的,一个加工条件集ti与其所有密度可达的对象构成一个聚类。
面向高速干切滚齿工艺样本集,将具体的滚齿工艺问题加入工艺样本集中,采用DBSCAN算法获得与滚齿工艺问题的加工条件参数相似度最高的工艺样本集。DBSCAN算法主要步骤如下:
(1)随机选取对象。从工艺样本集中选择任意一个工艺样本ti,利用式(2)计算出样本集中剩余样本与ti的距离Tdist,如果距离值小于E,则将此样本加入ti的邻域NE(ti)中。
(2)核心样本判断。若NE(ti)中的样本数目大于mpts,则标记为核心样本,建立对应的簇C,否则标记为边界点或者噪声,返回步骤(1)。
(3)对簇C中的其余工艺样本tk进行邻域计算,如果存在某样本ti也为核心对象,且其邻域点tk不在簇C中,则将ti加入簇C中。
(4)待所有工艺样本都迭代完毕并被标记以后,得到多个工艺样本聚类,按约束条件对包含待决策工艺问题的聚类进行筛选,得到相似工艺样本集。
2.4 基于改进NSGA-Ⅱ的工艺参数多目标优化
NSGA-Ⅱ是一种广泛应用于多目标优化的算法[14-16]。该算法时间复杂度低,具有较高的种群多样性,全局搜索能力强,通过引入第一前端的概念,保证筛选范围的同时保留最优个体,增强了算法的稳定性和鲁棒性。
本文考虑滚齿工艺参数优化决策的特点,采用改进的NSGA-Ⅱ算法(improved NSGA-Ⅱ),相比传统的NSGA-Ⅱ算法,最大的改进是引入最优前端个体系数和动态保留系数的概念,面向不同前端个体集,应用了不同的筛选策略,从而对优化后的Pareto非劣解集容量进行动态的控制:改进NSGA-Ⅱ算法能够基于各前端个体集的拥挤情况,对最优前端个体系数和动态保留系数进行动态的调控,从而保证算法中的优质个体得以保留,同时淘汰部分值域密集的前端个体集,以避免陷入局部最优的状况。
定义5 个体A支配个体B的判断准则是:若A的优化目标AO至少有一个元素比B的优化目标BO好且AO其余元素不比BO差。
定义6 非支配排序函数伪码为
FOR(inti=1;i<=N;++i){
FOR(intj=1;j<=K;++j)
IF(对Fj中的元素都无法支配Rti‖Fi==Ø)Fj×Add(Rti);}
式中,N为种群个体数;Rti为种群中的某个体。
定义7 前端保留数目计算函数为
Rt(Fi)=
(9)
其中,pf、gr、co为控制前端个体保留数目的比例系数,取值区间为[0,1];Nu为非支配排序后的前端总数;ceil()为圆整函数。面向高速干切滚齿工艺参数多目标优化的改进NSGA-Ⅱ算法流程图见图2,其主要步骤如下:
(1)t从0开始,将第t代种群Pt通过交叉、变异等筛选,产生下一代种群Qt,Qt与其父代Pt组合成种群Rt,其中,Qt和Pt的容量均为N。
(2)对Rt进行非支配排序,生成多个前端Fi。
(3)单独设置一个最优前端个体系数(Pareto-fraction),用以初步计算最优前端放入下一代种群的个体数目,对于其他前端的个体,则使用动态保留系数co计算该前端下一代种群数目。
(4)计算各个前端的拥挤度。前端内部拥挤程度越高,数据同质化程度高,则保留系数越低。通过设置不同的参数比例实现进一步优化。

图2 改进的NSGA-Ⅱ多目标优化算法流程Fig.2 Multi-objective optimization algorithm flow ofimprove NSGA-Ⅱ
(5)如果所有前端的保留数目之和小于N,则从最劣前端开始,以一个增量比例in扩大该前端的保留数,直到总保留数目大于或等于N。
(6)根据拥挤度高低从前端Fi中截取N-Pt+1个个体,使Pt+1种群大小为N,然后通过约束条件筛选产生下一代种群Pt+1,当迭代次数达到max_gen时,输出种群Pt+1,否则返回步骤(1)。
2.5 工艺参数多目标优化模型的求解
针对高速干切滚齿工艺参数优化,将工艺参数集P作为种群的个体,个体pi包含4个工艺参数:滚刀头数pi1、切削速度pi2、轴向进给速度pi3、滚刀转速pi4,改进NSGA-Ⅱ的适应度函数是GABP神经网络构建的预测模型,其输入是迭代优化后的工艺参数集PF,优化目标为OP。综上,面向加工能耗与刀具寿命的高速干切滚齿工艺参数优化数学模型为
F{GABP(R,P,OP),DBSCAN(P{pi1,pi2,…})}=
(maxT,minW)
(10)
pijmin≤pij≤pijmaxj=1,2,3,4
(11)
si1≤MAX_Tsi2=ELI_Q
(12)
其中,F表示改进NSGA-Ⅱ优化模型输入与输出的非线性映射关系;pij表示个体pi的工艺参数项;pijmax、pijmin分别是个体pi中各项工艺参数的最大值、最小值;si1、si2分别为pi中的加工时间与加工质量值;MAX_T、ELI_Q分别为加工时间下限值和质量合格值。具体流程如图3所示,高速干切滚齿工艺参数多目标优化决策主要步骤如下:
(1)滚齿工艺问题的确定。获取具体的工艺问题参数,采用DBSCAN算法得到与工艺问题的加工条件最相近的工艺样本集,经约束条件筛选后,构建多目标优化模型的输入区间。
(2)设定GABP算法参数,包括个体总数、个体长度、交叉概率、变异概率、各层节点数、迭代次数等。
(3)将样本集分为训练组和测试组样本,训练并验证GABP神经网络,得到最优的原始网络结构参数,再次使用加工工艺样本训练,构建加工效果预测模型。
(4)设定改进NSGA-Ⅱ的算法参数,包括迭代次数、个体总数N、个体长度L、交叉概率、变异概率、第一前端个体系数、动态保留系数等。
(5)随机初始化种群初始位置,得到一个N×L矩阵,对优化变量采用10位二进制编码,对每次输入和更新的种群分别进行编码与解码,由于优化变量有4个,所以个体长度是40位;种群每个个体数值在式(11)区间范围内,调用GABP神经网络计算适应度函数值,并记录这些解。
(6)通过选择、变异等筛选获得新一代种群,与父代种群合并后再进行支配度排序,设置各前端个体系数,根据个体拥挤度,将种群规模修剪至N。
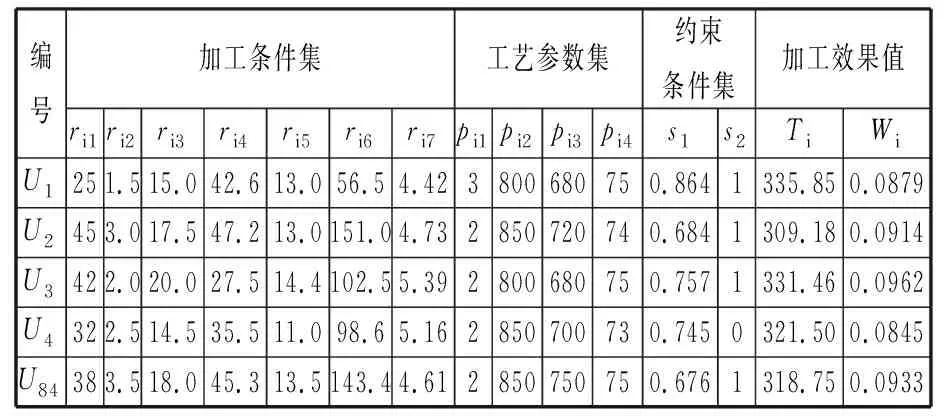
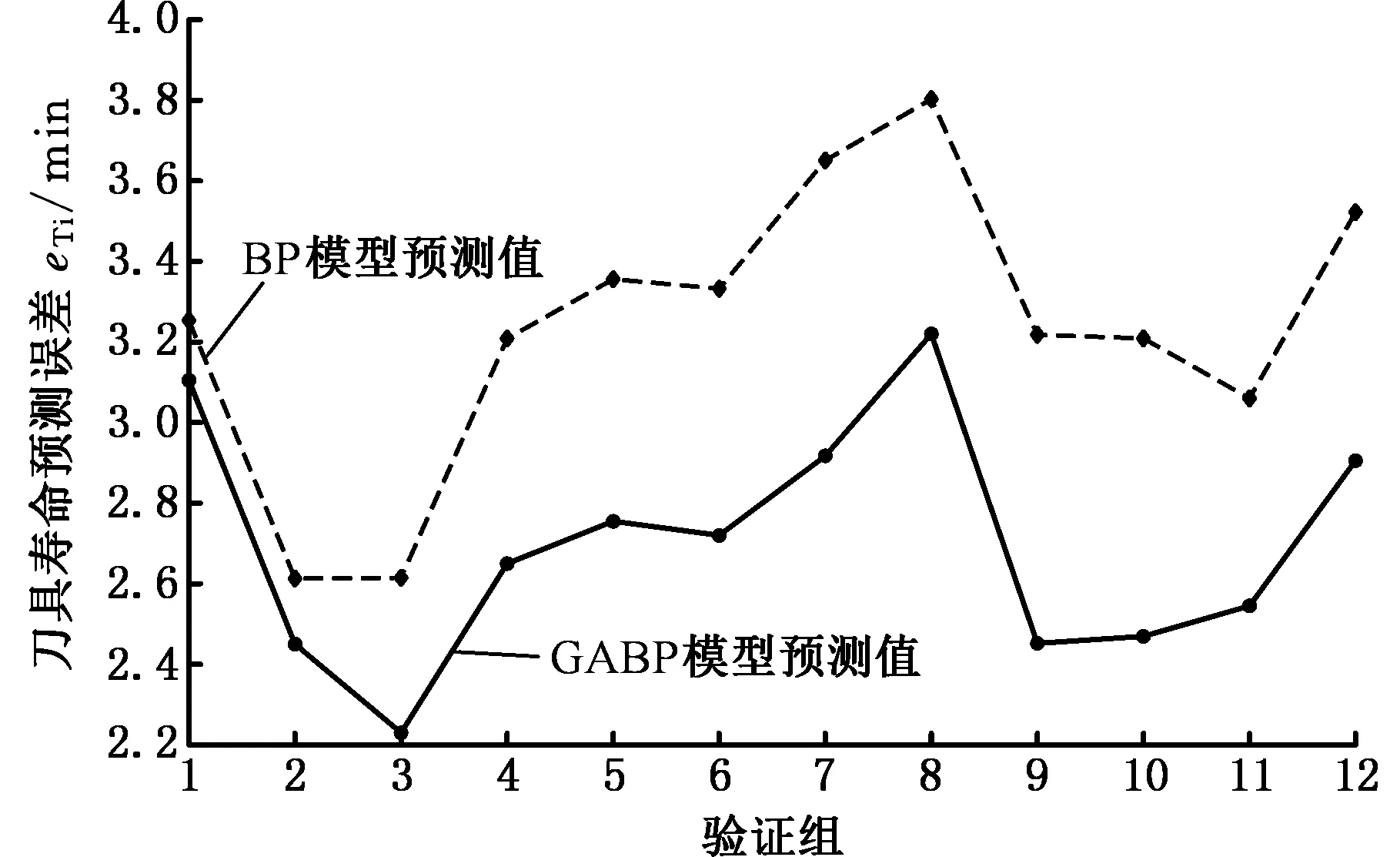
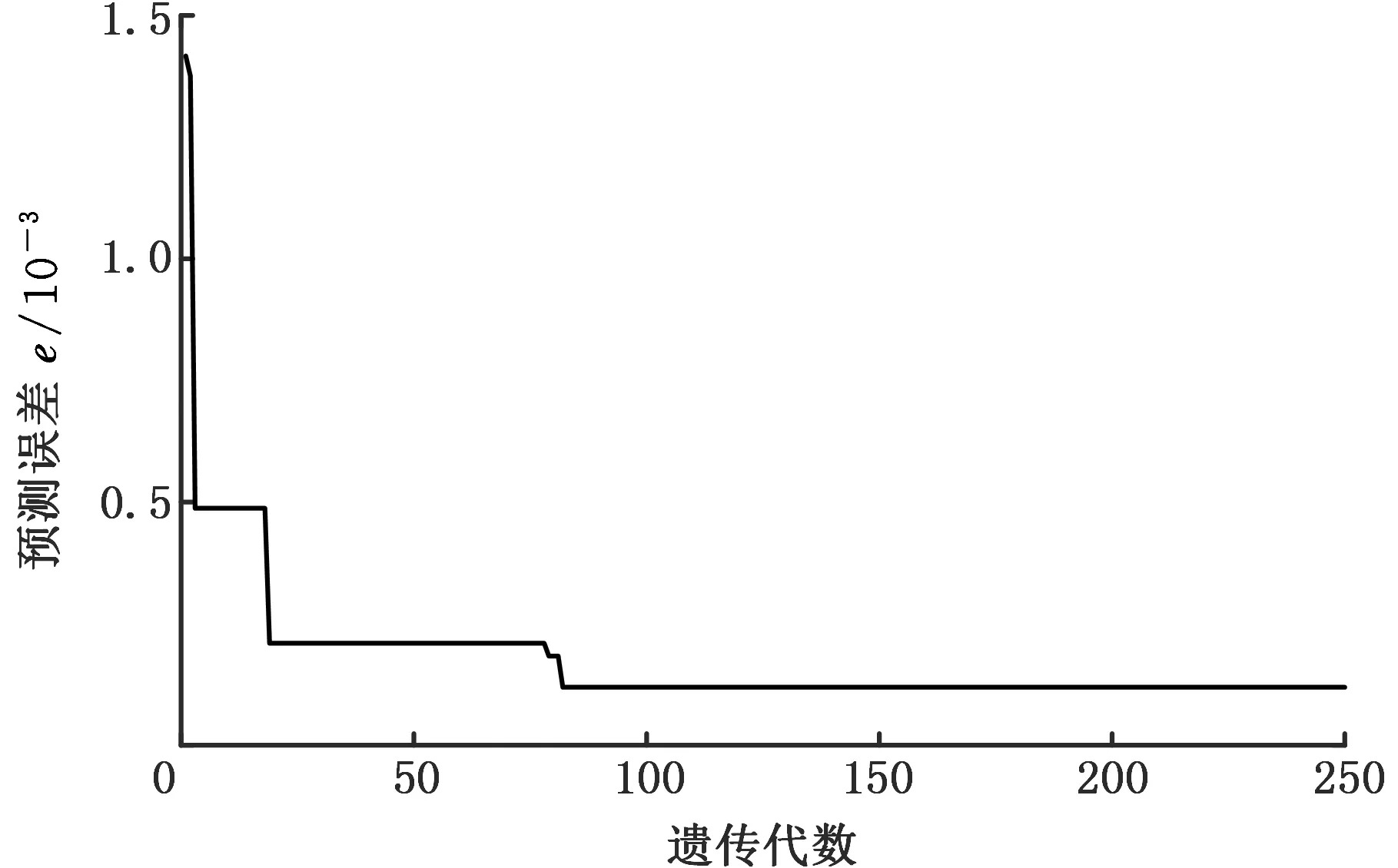
(7)将当前种群在式(12)范围进行筛选,如果K (8)获取最后一代种群中第一前端的工艺参数集PM与对应的优化目标数值集OPM,PM即针对待决策问题的Pareto最优解。 图3 高速干切滚齿工艺参数多目标优化决策流程Fig.3 Multi-objective optimization and decision flowof high speed dry hobbing parameters 本文以十一轴四联动数控高速干切滚齿机的84个工艺样本作为工艺样本集进行优化实验验证,为便于模型构建,将加工质量s2的合格值ELI_Q记为1,不合格值记为0,见表3。通过MATLAB程序来构建GABP神经网络预测模型。考虑到本文中神经网络的输出数为4,包括加工能耗、刀具寿命、加工质量、加工时间,将60个工艺样本作为训练组,12个工艺样本作为验证组,12个工艺样本作为测试组。此时IF节点数为12,OF节点数为2,根据式(2)取LF节点数为23,均方差曲线见图4,当最优循环次数为6时,均方差为10-6,最佳验证值为0.000 428 12,表明该网络稳定性较强。再使用测试组数据对比GABP神经网络与传统的BP神经网络的预测误差,结果如图5、图6所示,当GABP神经网络的输出平均误差为3.237和0.003 188时, BP神经网络的平均误差为2.701和0.004 908, 相比后者, 刀具寿命误差减小了16.56%, 加工能耗误差减小了35.04%。相比传统的BP神经网络,GABP神经网络进一步提高了网络的预测精度。神经网络算法迭代过程中的预测误差变化曲线见图7,由图7可知,GABP算法的收敛性较好。 表3 工艺样本集 图4 GABP优化后的均方差曲线Fig.4 Mean variance curve after GABP optimization 图5 GABP模型与BP模型关于预测刀具寿命的误差曲线Fig.5 Error curves of predicting tool life in GABPand BP models 图6 GABP模型与BP模型关于预测能耗的误差曲线Fig.6 Error curves of predicting energy consumptionin GABP and BP models 图7 GABP模型的预测误差变化曲线Fig.7 Prediction error change curve of GABP model 滚齿工艺问题的加工条件集R0={42,2,20,26.5,14.4,106.5,5.48}。对表3中工艺样本集采用DBSCAN算法,取mpts=4,得到容量为5的相似工艺样本集,见表4。 表4 相似工艺样本集 已知待优化滚齿工艺问题的相似工艺样本集R0,设约束条件的加工时间上限值MAX_T为相似工艺样本集的最大值。基于GABP和改进NSGA-Ⅱ算法的高速干切滚齿工艺参数多目标优化模型为 F{GABP(R,P,OP),DBSCAN(P{pi1,pi2,…})}= (13) (14) 改进NSGA-Ⅱ算法的参数设置如下:个体总数N=100,迭代次数T=200,前端个体系数pf=0.15,gr=0.3,co=0.4,某个体pi的各项工艺参数pi1、pi2、pi3、pi4的约束范围见式(14)。经多目标优化模型迭代后,得到关于工艺问题的Pareto最优解集,其加工效果如图8所示。将得到的Pareto解集与相似工艺样本集进行加工效果对比,见表5。由表5可知,从加工效果来看,Pareto解集的加工效果整体优于相似加工样本集,因此,多目标优化模型达到了加工能耗与刀具寿命的综合最优。 图8 针对具体工艺问题的Pareto最优解集的加工效果Fig.8 Processing effect of Pareto optimal solution setfor specific process problems 表5 加工效果对比 (1)本文建立了以最大刀具寿命和最小加工能耗为优化目标,以滚刀头数、滚刀转速、切削速度和轴向进给速度为优化变量,以加工时间、加工质量为约束的多目标优化模型。 (2)本文从实际加工工艺样本出发,通过DBSCAN聚类算法获取滚齿工艺问题对应的相似加工样本集,构建多目标优化模型输入区间,利用GABP神经网络构建加工优化目标值的预测模型并作为多目标优化模型的适应度函数,使用改进NSGA-Ⅱ算法对多目标优化模型进行迭代求解,通过优化结果对比,证明该方法能够实现加工能耗与刀具寿命的综合最优。 (3)本文实例验证部分以60个样本作为训练集,考虑到实际加工生产的情况较为复杂,企业实际准备的样本较少,对于小样本(样本容量小于40)的情况,基于本文方法提出两点建议:首先需要增加隐含层神经元个数,从而提高神经网络的拟合能力,但需要注意避免过拟合,同时,增加隐含层神经元个数需要付出训练时间增加的代价;其次,筛选工艺样本作为训练集时需要保证训练集能够覆盖值域,以提高训练集的全面性。 由于数控加工刀具类型多样,本文主要对特定刀具的高速干切滚齿工艺参数优化进行了研究,在实际生产过程中,同一批次的工件往往也需要应用多种刀具进行加工,因此,考虑到具体刀具材料特性等不尽相同,如何将本文方法有效应用到通用类型刀具的加工参数优化决策过程中,是下一步研究的重点。
3 实例验证



(maxT,minW)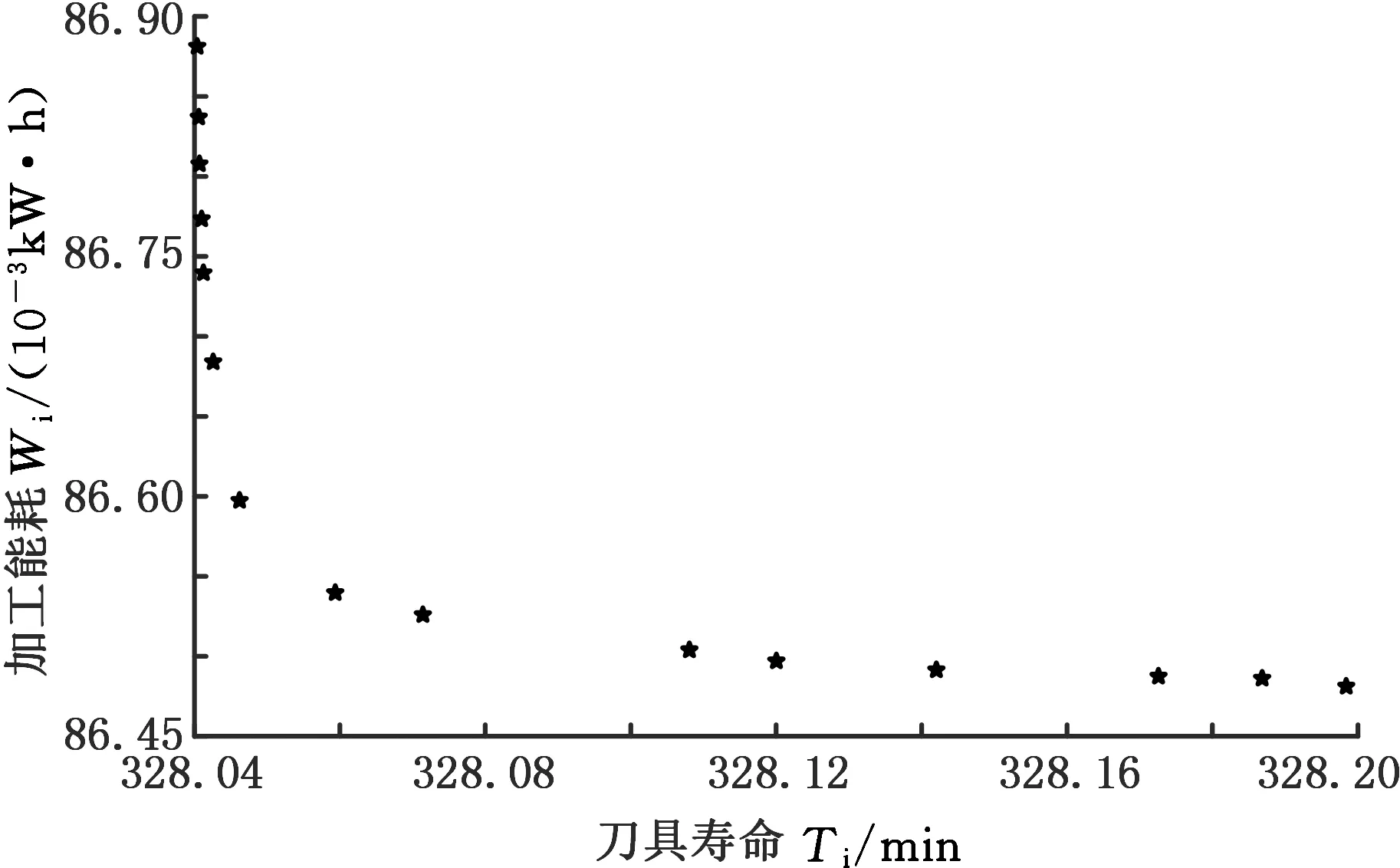

4 结论
