水力性质和降雨模式对黄土边坡变形规律的影响

叶万军，崔晨阳，高 崇，董 琪，景宏君，邓友生

(1.西安科技大学 建筑与土木工程学院，陕西 西安 710054；2.中铁十九局集团 轨道交通工程有限公司，北京 101300； 3.陕西科技控股集团有限责任公司，陕西 西安 710077)

0 引言

降雨与非饱和土边坡稳定的关系密切且复杂，近年来，降雨诱发型滑坡的成因机理[1-2]已被广泛认可，但对外部降雨条件与内部土体性质两大类影响因素相对作用程度的认识仍不尽相同。在降雨模式方面，文献[3]基于二维渗流分析与极限平衡法，表明降雨强度对膨胀土边坡影响显著性与坡体饱和渗透系数有关。文献[4]通过统计分析深圳市地灾资料，认为暴雨与滑坡活动关系密切。文献[5]基于模型试验提出“门槛累积雨量”的概念，并认为低强长历时降雨更易诱发边坡滑动。文献[6]通过对前期降雨排水时间的拟合研究，提出暴雨条件下边坡破坏与排水周期无关，失稳时间相近。文献[7]探索前期降雨对砂土与黏土边坡稳定性的影响规律，提出砂坡对高强短时前期降雨更敏感，而黏土边坡对低强长时前期降雨更敏感。文献[8]提出边坡无支护条件下，长时小雨较短时暴雨的入渗影响范围更深。文献[9]引入破坏接近度的概念，从多角度分析雨强、雨型与持时的影响。文献[10]基于模型试验提出间断型强降雨下，坡体表现出滑移-拉裂式失稳；而持续型强降雨下，为蠕滑-拉裂式破坏。以上研究主要集中在降雨强度、降雨类型、降雨持时与前期降雨等因素的影响，未综合考虑相同降雨对不同类型土坡的影响。

除了外界降雨模式外，服役期边坡破坏很大程度上取决于内部土体性质的综合影响。非饱和土吸力特性与三相组成及力学特性联系密切，但针对土水特性对稳定性综合影响的研究甚少。文献[11]基于不同含水率下土体的强度折减，计算分析含水率变化对边坡稳定性的影响。文献[12]运用Seep/W分析不同土水特征参数对坡体基质吸力的影响，但其未引入本构关系进行边坡稳定性分析。文献[13]利用Seep/W探索热带地区残积土的水力性质参数对边坡破坏的影响程度，但该地区地下水位较浅，与黄土塬区差异较大，对陕北地区边坡稳定性分析参考价值有限。文献[14]分析前期降雨类型与土水特征参数改变时坡体稳定性响应情况，但其饱和渗透系数固定，且未综合分析降雨环境对稳定性的影响。文献[15]借助Geo-Studio分析VG模型参数变化对边坡渗流与稳定性的影响，但其仅针对无支护理想边坡展开研究。

综上可知，目前服役期边坡稳定性影响研究主要集中在降雨与土体饱和渗透系数方面，且多为地下水位深埋较浅的情况，而实际非饱和土的土水特性是由多个参数共同决定的，其与外界降雨综合影响边坡稳定性，故针对土体水力特性与降雨模式，可以对坡体渗流场与位移场分布规律影响程度进行综合研究。本文结合陕北延安地区实测降雨资料与抗滑桩边坡实例，基于ABAQUS有限元软件，建立地下水位深埋坡体降雨过程的数值计算模型，设置系列参数变量，探索Van Genuchten(VG)模型参数、饱和渗透系数、降雨强度、降雨类型与降雨持时对坡体稳定性的影响程度，可为滑坡灾害防治工作提供一定的理论参考。

1 工程概况

某抗滑桩边坡位于陕西省延安市宜川县，属陕北黄土高原丘陵沟壑区，位于暖温带半湿润区，具有明显的大陆性季风气候特征，地下水类型主要为黄土孔隙水和基岩裂隙水。根据钻孔揭露，地层自下而上依次为：上三叠统延长群瓦窑堡组、第四系中更新统黄土、第四系上更新统黄土与全新统滑坡堆积层。滑面所在地层主要为第四系中更新统黄土，呈浅棕色，质地坚硬，偶见有钙质结核。根据室内常规试验测定结果，黄土的基本物理力学性质指标见表1。依据工程地质勘察资料，对坡体进行分级放坡，并设置抗滑桩和挡土板作永久性支挡，各支护部件基本尺寸如表2所示。

表1 黄土的基本物理力学性质指标

表2 各支护部件基本尺寸

2 降雨过程的数值模拟

2.1 非饱和流固耦合数值实现原理

非饱和土力学理论是降雨条件下土质边坡稳定性研究的根基。其中，准确描述基质吸力与含水量关系的土水特征曲线至关重要，可用于推测非饱和土渗透系数等相关特性。在应用较广的模型中，Van Genuchten模型能有效拟合曲线形状，且其用于非饱和黄土中适应性良好[15-16]。故本文亦选定这种形式，采用土水特征曲线与渗流系数模型为[17]：

(1)

k(Se)=kskr(Se)=ksSe0.5[1-(1-Se1/m)m]2，

(2)

其中：Se为有效饱和度；θ为体积含水量，%；θr为残余含水量，%；θs为饱和体积含水量，%；a为进气值的倒数，kPa-1；φ为基质吸力，kPa；n为当基质吸力大于进气值时，土中水的流出率，与孔径分布有关；m与曲线整体对称性有关，可近似取1-1/n；ks为饱和渗透系数，m/s；kr为相对渗透系数，m/s。

非饱和流固耦合计算采用ABAQUS软件专门的孔隙流体渗透/应力耦合模块实现，本文基于选定的土水特征曲线与渗流系数模型，利用内置的流固耦合模块，通过定义不同的材料参数与荷载条件进行仿真计算，分析不同降雨入渗条件下，不同时刻、各类土质边坡坡体的孔压场与位移场分布规律，研究各类土质边坡不同降雨模式下的稳定性差异。

2.2 边坡计算模型与边界条件

基于上述黄土边坡非饱和流固耦合分析原理，采用ABAQUS软件建立降雨过程的数值计算模型。

延安某抗滑桩边坡降雨条件现场监测结果用于验证本次数值模型，故建模时选取该边坡典型区段进行非饱和渗流计算。为削弱边界效应带来的影响，坡体模型尺寸定为12 m×65 m×44 m(长×宽×高)，抗滑桩模型尺寸为2 m×3 m×14 m(长×宽×高)，挡土板模型尺寸为4.0 m×0.4 m×4.0 m(长×宽×高)。围岩采取Mohr-Coulomb模型，支护结构中抗滑桩与挡土板采取弹性模型，参数采取表1与表2的室内试验结果。在网格划分中，模型采取对称网格，土体结构采取Pore-Fluid/Stress的C3D8P单元，抗滑桩与挡土板采用3D Stress的C3D8R单元。模型尺寸与网格划分效果图见图1。

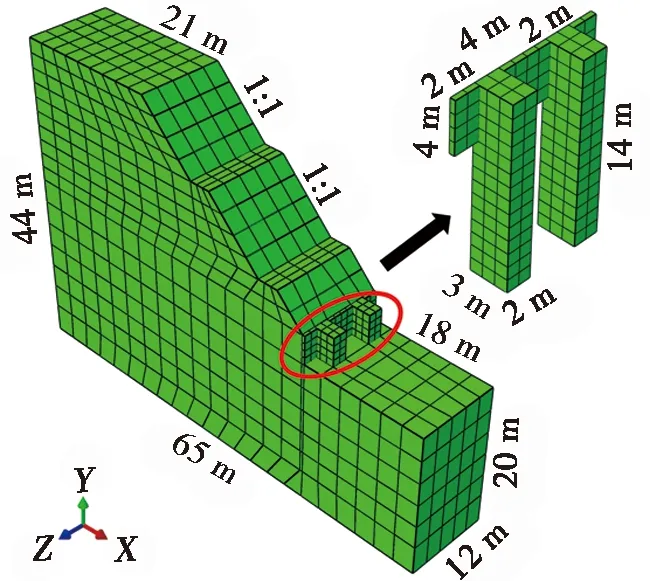
图1 模型尺寸与网格划分效果图

模型中定义XOY面为边坡断面，Z轴为挡土板走向的方向，其边界条件为：下底面限制任意方向移动，四周限制法向变形，坡面选择入渗边界，下底面及四周边界设为自由渗出边界，仅支持孔隙水从边界渗出，限制渗入。降雨前，坡体处于静水条件下稳态。延安地区地下水位埋深较大，依据当地地下水位动态监测结果[18]，将初始地下水位预设在埋深16 m处，水位以下净水孔压力随深度线性增加。

2.3 有限元模型的验证

在自然降雨过程中，通过将振弦式孔隙水压力计埋设在坡面不同深度处(1 m、2 m、3 m)，对边坡进行孔压监测，通过TF-CX-901F型测斜仪量测坡体深部位移情况。此处通过对7月某次自然降雨(日降雨量110 mm/d，持续2 d)进行模拟，并将计算得到的位移变化与实测资料进行对比，用以验证模型的可靠性。测斜仪现场监测图见图2。图3对比了实际地层降雨条件下坡体深部位移实测值与计算值。

由图3可以看出：位移计算值与实测值吻合较好。通过以上分析可知：本文建立的数值模型用于分析自然降雨下边坡的稳定性问题是合理的。下文将用该模型进行考虑土体水力特性与降雨模式的黄土边坡变形规律研究。

2.4 数值模拟方案

边坡几何形状与初始地下水位位置主要影响坡体安全系数初始值，服役期实际破坏条件很大程度上取决于施加在坡面上的降雨与土体性质[19]，故本文主要探讨外界降雨模式和内部土体水力特性对非饱和土边坡稳定性的影响。选取Van Genuchten模型参数a、参数n与饱和渗透系数ks，为本文研究的水力性质变量，选取降雨强度、降雨类型与降雨持时为降雨模式变量。为提高分析结果的工程实用价值，结合陕北地区降雨特征[20]，采用Soils瞬态分析步进行降雨入渗全过程分析。

选取陕北地区分布广泛的黄土，根据饱和渗透系数ks数量级上的差异，将其分为排水良好与排水不良两类。为削弱土体初始抗剪强度特性对边坡稳定性的影响，土体均采用Mohr-Coulomb屈服准则，参数研究中仅改变水力参数，其余土性参数保持不变。表3列出了参数研究中涉及的可变参数，每一种影响因素考虑4个水平，其余因素保持不变。

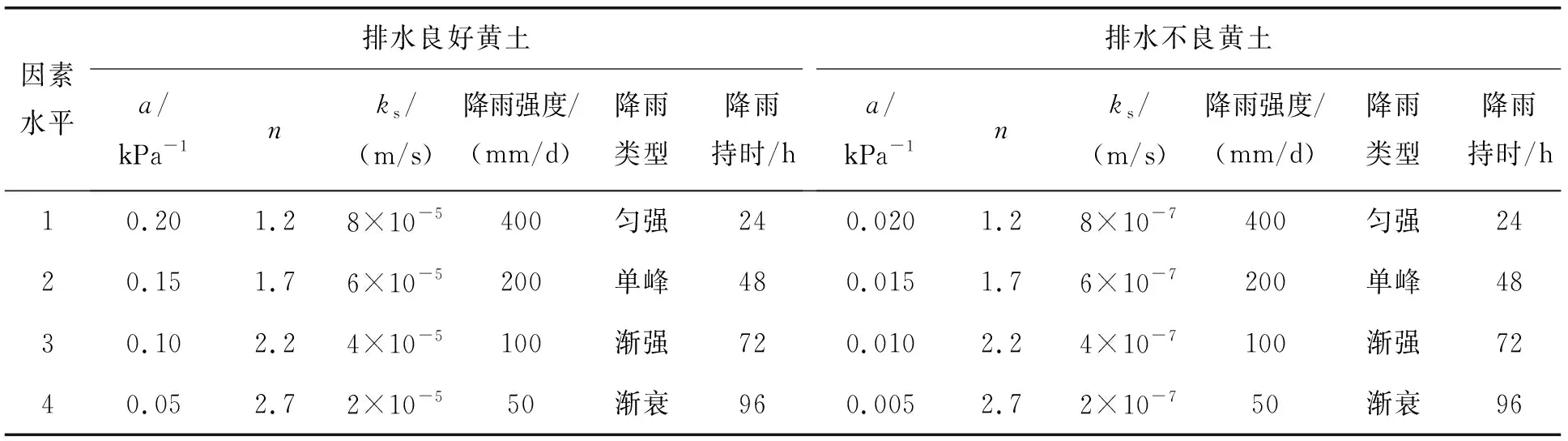
表3 数值试验选定影响因素及水平

3 计算结果与分析

尽管所有参数条件的边坡拥有相同的模型尺寸与初始地下水位，但每种黄土类型对施加的土水特征参数、饱和渗透系数等条件响应不同，因此，降雨前坡体位移分布情况不同。为了获得统一化可比数据，在分析不同参数条件下的计算结果时，选取坡体变形最大点提取数据展开分析。

3.1 水力参数影响程度分析

3.1.1 VG模型参数a的影响

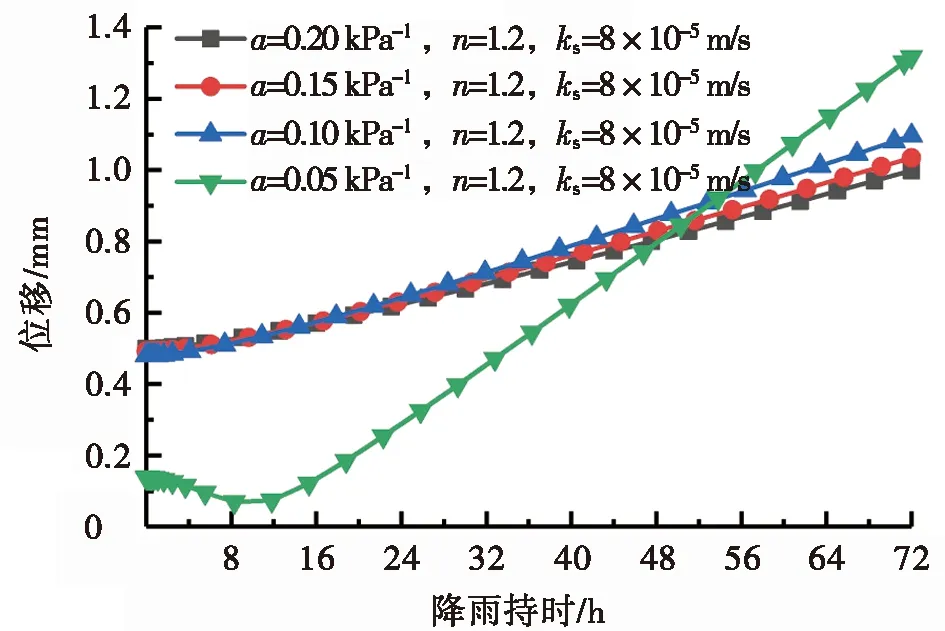
图4为VG模型参数a变化时坡体位移时程曲线。图4a与图4b分别展示了VG模型参数a变化时，排水良好与排水不良的土质边坡变形最大点位移随降雨持时的变化规律。

图4中的位移变化是由降雨强度400 mm/d、降雨72 h引起的。由图4可知：无论土体排水性如何，参数a较小时，坡体变形随降雨持时的上升速度更快且最终位移更高。相对而言，对于排水良好的坡体，相同降雨条件下最终位移差异较小，土体参数a的变化对边坡稳定性影响微弱。对于排水不良土体的坡体，最终位移差异明显，土体参数a的变化对坡体稳定性影响显著。

在土-水特征曲线模型中，参数a是与进气值有关的试验参数。参数a的值越低，进气值越大，相同基质吸力下体积含水量越高。在非饱和土中，水仅在孔隙水所占空间中流动，故体积含水量较高的土体中水的运动更快。饱和渗透系数一定的情况下，参数a较低的土体在相同基质吸力下具有较高的渗透系数，雨水进入土体的入渗能力更强，则坡体受降雨影响范围更大，入渗更深。因此，对于参数a值较低的土体，变形随降雨持时的上升速度更快。

3.1.2 VG模型参数n的影响

图5为VG模型参数n变化时坡体位移时程曲线。图5a与图5b分别展示了VG模型参数n变化时，排水良好与排水不良的土质边坡变形最大点位移随降雨持时的变化规律。

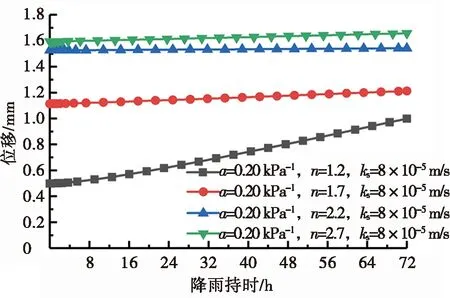
图5的位移变化是由降雨强度400 mm/d、降雨72 h引起的。由图5可知：对于排水良好的土体，参数n变化时，随持续降雨坡体加剧的变形量并不显著，最终变形量也大致相同，而对于所有排水不良的土体，变形量的增加幅度较大。即参数n的变化对排水良好的土质边坡稳定性影响微弱，对排水不良土体的坡体稳定性影响较显著。但总体而言，无论土体排水性如何，参数n较低时变形随降雨持时增加的上升速度更快。

VG模型参数n与孔径分布有关，影响土壤水分特征曲线内弯点的斜率。参数n越大，孔径分布越小，土壤水分特征曲线内弯点的斜率越陡。当基质吸力低于进气值时，n值较高的土体体积含水量较高；当基质吸力高于进气值时，n值较高的土体体积含水量较低。故降雨作用时坡体的变形响应取决于土体的初始基质吸力状态。鉴于延安地区地下水位较深，降雨前坡体非饱和土的初始基质吸力已经高于进气值，故n值较低的土体体积含水量较高，入渗深度较大，相同情况下变形随降雨时长的上升速度更快。这是地下水位深埋边坡与普通土质边坡，如热带地区边坡[13]相异之处。

3.1.3 饱和渗透系数ks的影响

图6为饱和渗透系数ks变化时坡体位移时程曲线。图6a与图6b分别展示了排水良好和排水不良的土体在不同饱和渗透系数ks下，变形最大点位移随降雨持时的变化规律。

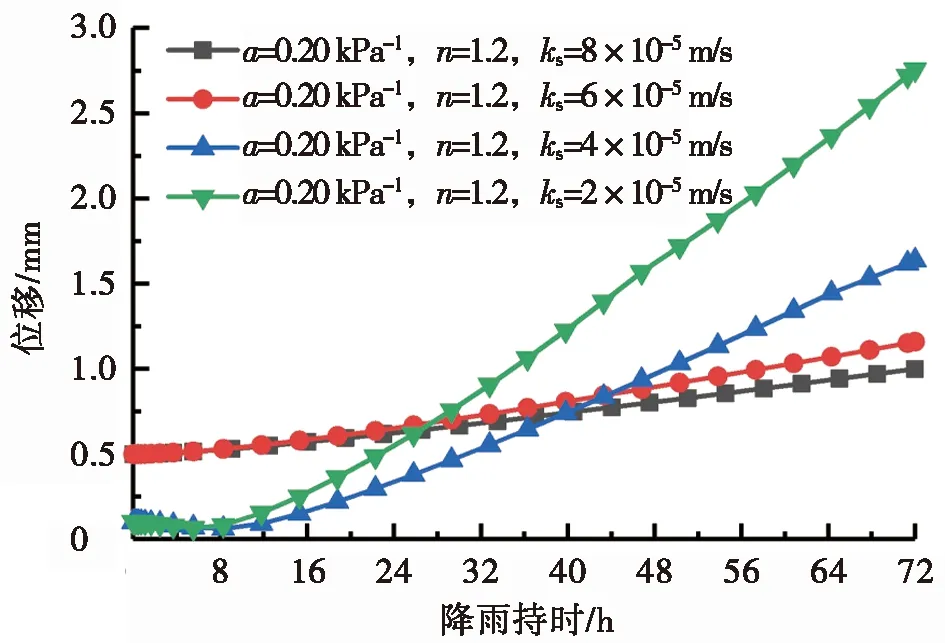
图6的位移变化是由降雨强度400 mm/d、降雨72 h引起的，排水良好土体饱和渗透系数大于选定雨强，排水不良土体的反之。从图6中可以看出：饱和渗透系数ks变化时，对于排水良好的土体，随降雨持时增加，变形量的加剧并不显著，最终变形量差距不大；而对于所有排水不良的土体，变形量增加的幅度较大。即饱和渗透系数ks的变化对排水良好土质边坡的稳定性影响微弱，对于排水不良土体的坡体稳定性影响较显著。相较而言，无论土体排水性如何，相同降雨条件下饱和渗透系数ks较低时坡体最终变形量较大。

对饱和渗透系数不同的坡体而言，降雨强度与饱和渗透系数相对关系至关重要。排水不良土体的渗透系数小于降雨强度，坡面土体体积含水率很快达到饱和，部分降雨在坡面形成短暂积水，孔隙气压力增加，降雨入渗难度较大，入渗深度较浅，表层土体孔隙水压力与基质吸力变化幅度反而较大。而排水良好土体的饱和渗透系数大于降雨强度，气体可以溢出坡面，湿润锋推进较快，坡体入渗深度较深，但表层土体饱和度始终不高，孔隙水压力变化较小，为较大负值，基质吸力减小作用微弱，保持在较大值，故排水良好土体坡体在同等降雨条件下变形值较小。总体而言，无论降雨强度如何，土体的渗透系数越大，雨水的入渗深度越深，相对使得坡体浅层基质吸力更高，最终坡体变形量便相对较小。

3.2 降雨参数影响程度分析

3.2.1 降雨强度的影响

图7为降雨强度q变化时坡体位移时程曲线。图7a与图7b分别为排水良好和排水不良的土体，在降雨强度不同时变形最大点位移随降雨持时的变化规律。

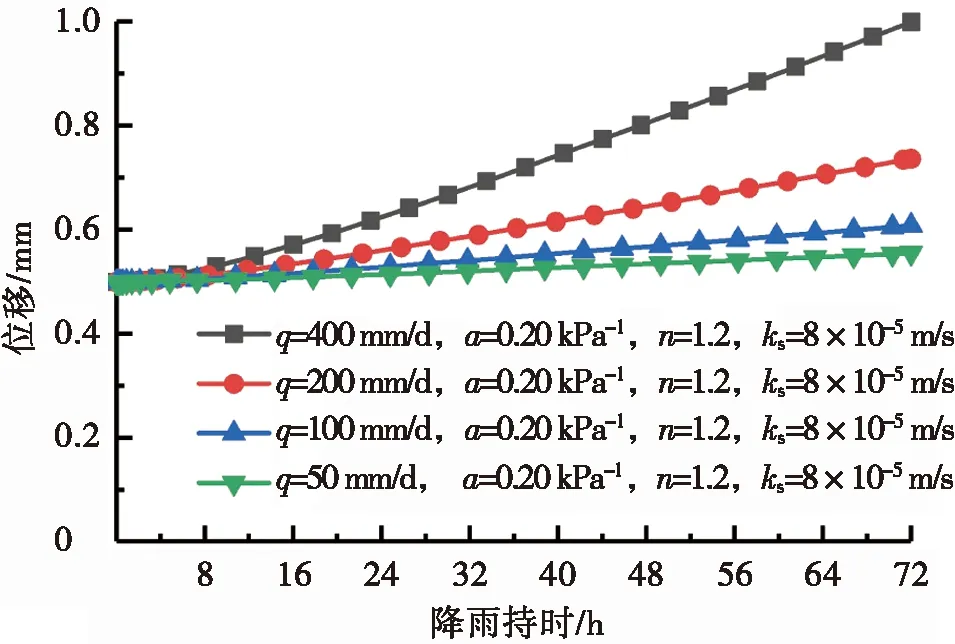
鉴于黄土地区降雨多暴雨且雨季集中，根据降雨量等级划分标准[21]，选择400 mm/d(特大暴雨)、200 mm/d(大暴雨)、100 mm/d(暴雨)与50 mm/d(大雨)4种降雨强度，分析同一土体不同降雨强度下位移变化差异。从图7中可以看出：不同降雨强度对坡体位移响应差距较大。无论土体排水性如何，相同降雨时间内降雨强度越大诱发坡体位移越大，且随着降雨强度的增加，位移增大幅度逐渐增大。分析可知：雨强越大，相同时间内渗入坡体的雨量越大，坡体相同位置处土体越饱和，孔隙水压力越大，基质吸力消散越快，故坡体位移越大，稳定性越低。

3.2.2 降雨类型的影响

图8为降雨类型变化时坡体位移时程曲线。图8a与图8b分别为排水良好和排水不良的土体，在强降雨类型不同时变形最大点位移随降雨持时变化规律。

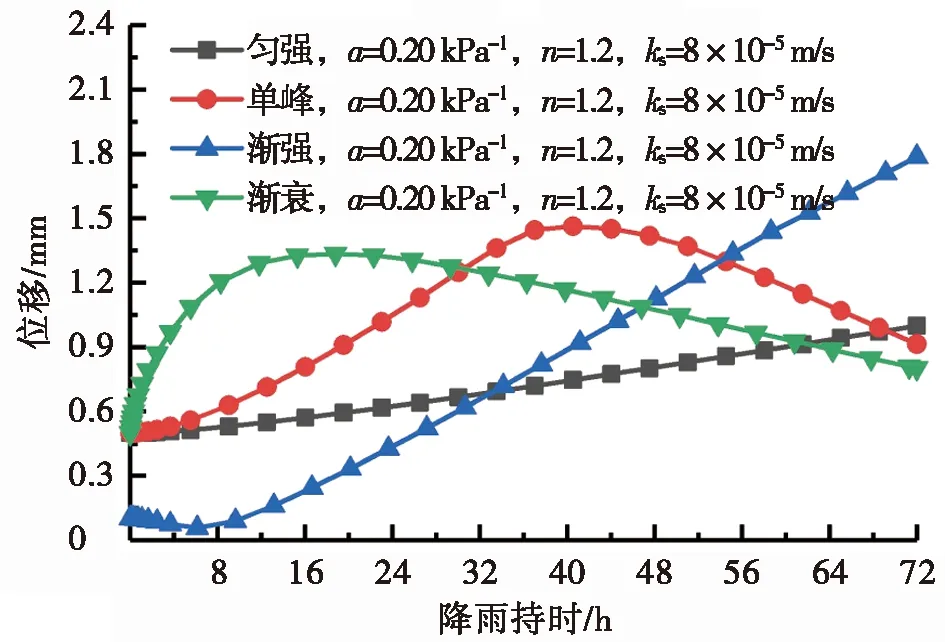
伴随着降雨的进行，相同总降雨量下不同降雨类型有不同的雨量分配特征。72 h总降雨量相同的条件下，选择匀强、单峰、渐强与渐衰4种降雨类型，分析同种土体不同强降雨类型下位移变化差异。从图8中可以看出:相同降雨强度下不同降雨类型对应的位移最大值出现时间不一致,但均与降雨峰值时间有关。匀强与渐强型位移最大值出现在降雨停止时，单峰与渐衰型位移最大值出现在降雨峰值时间附近。

无论土体排水性如何，坡体位移与降雨强度时间呈正相关。降雨24 h时，坡体变形程度呈现出渐衰型>单峰型>匀强型>渐强型，这是由于此时渐强型降雨强度最低，故位移响应速度最慢，而渐衰型初始时间降雨强度最大，后期强度有所衰减，孔隙水压力减小，而基质吸力增强，故位移呈现先增大后减小的状态，变形回弹。降雨72 h后，坡体变形程度呈现出渐强型>匀强型>单峰型>渐衰型，这是由于渐强型与匀强型中后期仍存在较大降雨强度，土体孔隙水压力持续增加，基质吸力衰减，由此引发坡体位移增大。总体而言，渐强型降雨结束后坡体位移最大，匀强型与单峰型次之，渐衰型最小。可见，累计降雨量与降雨持时一定的情况下，边坡在渐强型降雨类型下更易发生失稳破坏，工程实际中应给予重视。

3.2.3 降雨持时的影响

图9为降雨持时t变化时坡体位移随埋深变化曲线。图9a与图9b分别展示了不同降雨持时下,排水良好和排水不良的土体坡体位移随埋深变化规律。

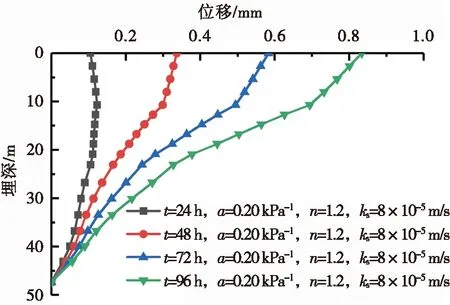
图9的位移变化是由降雨强度400 mm/d、匀强型降雨引起的。由图9可以看出：随着降雨持时的增加，无论土体排水性如何，坡体入渗深度均随之加深。降雨过程中，边坡浅层土体最先受到影响，位移出现较大变化。随着降雨持时的增加，累计降雨量不断增大，深部土体位移亦出现响应，但随着埋深的加深，位移逐渐减小。对比土体不同排水特性下位移随埋深变化曲线，分析可知排水良好土体降雨入渗较快，坡体深部响应较快，排水不良土体浅层位移变化明显，这主要是由土-水特征曲线不同引起的，前文已分析。

3.3 各参数影响程度分析

图10a～图10d分别为各个参数变化下坡体孔隙水压力随埋深的变化曲线图，可用于分析参数变化对降雨入渗条件下坡体渗流场的影响程度。

对水力参数而言，水力参数a是与土体进气值有关的试验参数，其值越低，进气值越大。由图10可以看出：对于饱和渗透系数较大的排水良好土体，参数a变化对孔隙水压力计算结果影响微弱；对于饱和渗透系数较小的排水不良土体，参数a越低，降雨入渗速度越快，相同埋深下负孔隙水压力值越高，基质吸力越低，坡体最终变形量较大。水力参数n与土体孔径分布有关，其值越大，孔径分布越小，土壤水分特征曲线内弯点斜率越陡。对初始地下水位深埋边坡，与参数a规律类似，参数n越低，埋深一定时，负孔隙水压力值越高，基质吸力越低，相同情况下变形随持续降雨上升速度更快。无论土体排水性如何，饱和渗透系数ks越低，埋深一定时负孔隙水压力值越高，基质吸力越低，相同情况下坡体最终变形量较大。

对降雨参数而言，降雨强度直接影响坡体入渗量，降雨强度越大，埋深一定时，负孔隙水压力值越高，基质吸力消散越快，相同情况下坡体最终变形量较大。降雨类型影响雨量分配状态，降雨总量与降雨持时一定的情况下，降雨结束后4种降雨类型时坡体孔隙水压力随埋深变化规律各不相同，相对而言，无论土体排水性如何，影响范围内渐强型孔隙水压力最高，渐衰型孔隙水压力最低。降雨持时影响降雨总量，分析可知：降雨持时越长，埋深一定时孔隙水压力值越高，基质吸力消散越快，坡体最终变形量较大。

以孔隙水压力变化情况为依据，分析可知对于排水不良土体，各参数变化影响程度为：降雨持时>降雨强度>VG模型参数a>降雨类型>饱和渗透系数>VG模型参数n。对于排水良好黄土而言，坡体孔隙水压力状态对参数变化不敏感，相对而言影响程度为：饱和渗透系数>降雨类型>VG模型参数n>降雨持时>降雨强度>VG模型参数a。总体而言，VG模型参数变化对排水不良土体坡体影响更显著，土体饱和渗透系数与降雨参数对排水良好和不良的坡体稳定性均有独特影响。

4 结论

(1)对水力参数而言，VG模型参数a是与进气值有关的试验参数，参数a值较低的土体，坡体变形随降雨历时上升的速度更快，最终位移值更高；VG模型参数n与孔径分布有关，参数n越小，孔径分布越大，土壤水分特征曲线内弯点斜率越缓。对地下水位深埋边坡而言，参数n值较低的土体坡体变形上升速度更快；相同降雨条件下，饱和渗透系数ks较低时，坡体最终变形量较大。

(2)对降雨参数而言，相同时间内降雨强度越大诱发坡体位移越大，且随着降雨强度的增加，位移增长幅度逐渐增大；降雨类型变化时，坡体位移与降雨强度时间呈正相关；随着降雨持时的增加，累计降雨量不断增大，坡体入渗深度随之加深。埋深一定时，降雨持时越长，孔隙水压力值越高，坡体最终变形量越大。

(3)以孔隙水压力变化情况为依据，排水不同，坡体对参数变化敏感程度不同。VG模型参数变化对排水不良土体坡体影响更显著，而土体饱和渗透系数与降雨模式参数对排水良好和排水不良的坡体稳定性均有独特影响。

(4)累计降雨量与降雨持时一定的情况下，排水不良土体坡体在外界渐强型降雨类型下，或者土体VG模型参数a与饱和渗透系数ks较低时，更易发生失稳破坏，滑坡灾害防治工作中应给予重视。