一维非幺正PT对称量子行走的拓扑特性

谭悦，李志坚

（山西大学 理论物理研究所，山西 太原 030006）

0 引言

量子力学中可观测的力学量由厄米算符表示，其本征值是实数，对应物理测量值。然而，有些体系的哈密顿量是非厄米的，如具有耗散的光波导[1-2]、光晶格耦合的 LRC 电路[3-4]、单模激光器[5-6]等体系，此类系统的哈密顿量如果存在空间和时间相继反演的对称性，简称PT对称性[7-9]，则非厄米哈密顿量会出现实的本征值。近年来，人们研究了幺正系统量子行走的传输特性。同样，由于增益损耗的影响，量子行走的时间演化算符会变为非幺正算符，例如人们在光纤环路上实现了非幺正量子行走，是通过附加的光学放大器和等效衰减器来控制增益和损耗[10]得到的。目前，开放量子系统、无序系统、拓扑绝缘体，具有复折射率的光学系统等领域的非厄米系统的PT对称性引起人们的广泛关注[11-13]。

具有PT对称性的系统往往会表现出非平庸的拓扑特性。由于拓扑绝缘体或超导体[14-15]等天然材料很少，所以人们构建了许多人造系统，可以利用Zak相位[16]、绕数、Berry相和陈数等拓扑不变量描述系统的拓扑性质。在对幺正量子行走[17]的研究基础上，人们也对非幺正量子行走的拓扑特性开始了研究[18-19]。本文将通过引入增益损耗算符，实现非幺正PT对称量子行走，在分离时间量子行走[20]中的硬币算符和条件平移算符中各引入一个可控参量，构成二维的参数空间，给出系统在该空间的拓扑相图。

1 非幺正PT对称量子行走及相图

一维分离时间量子行走的单步时间演化由硬币算符Cθ和条件平移算符Sφ相继作用产生，即

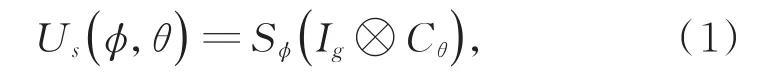
其中Ig为位置空间的单位算符，Cθ为硬币空间的硬币算符，在本文中选取硬币算符为沿着y方向旋转θ∈ (-π，π)角的旋转算符，形式为

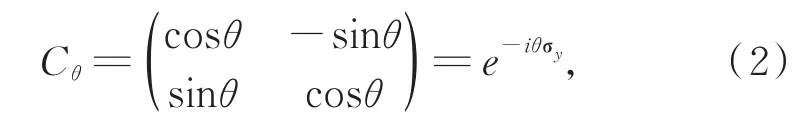
条件平移算符Sφ表示为

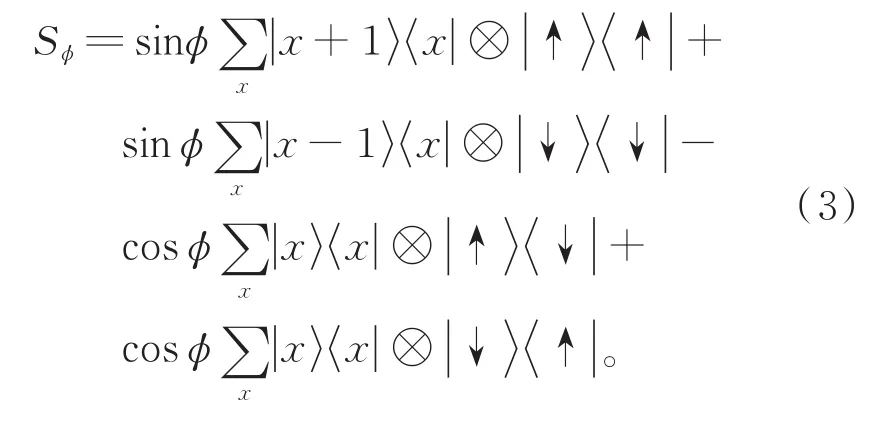
在条件平移算符（3）中引入一个参数φ∈(-π，π)，当输入的硬币态不发生翻转时，量子行走以概率幅sinφ向右（向左）行走，以概率幅cosφ保持在原来的位置不动。在光学系统中，光信号在光纤光路中会发生增益损耗[13]，本文引入增益损耗算符，（4）当硬币态为时，系统以eτ指数增益，当硬币态为时，系统以e-τ指数衰减。τ≠0时，增益损耗算符G是一个非幺正算符，非幺正量子行走的时间演化算符定义为

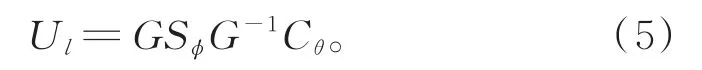
PT对称算符由宇称算符P和时间反演算符T的乘积构成。宇称算符是指空间对称算符，宇称算符P是一个线性幺正算符。在宇称对称变换下，坐标和动量算符满足变换关系时间反演算符T是一个反线性算符，其中包含取复共轭算符κ的操作，满足变换关系若 定 义

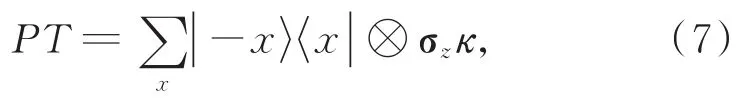
则Upt满足关系

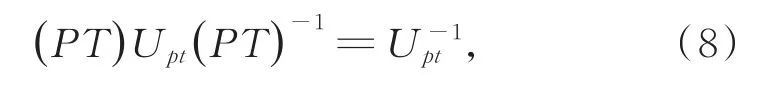
表明Upt描述的量子行走具有PT对称性。

演化算符Upt可以表示为Upt=exp(-iHeff)的形式，其中Heff是Upt的生成元。Upt的非幺正性决定了有效哈密顿量Heff是非厄米的。令是Upt的本征矢，相应的本征值为λ，即有

对算符Upt作傅里叶变换，在动量空间可表示为

其中Ic是硬币空间的单位矩阵，σi(i=x，y，z)是泡利矩阵，系数ln(n=0，1，2，3)分别为

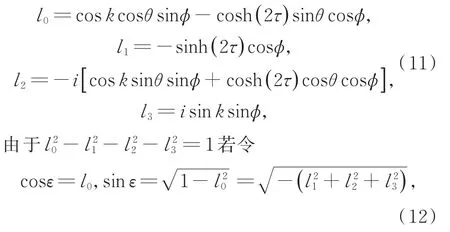
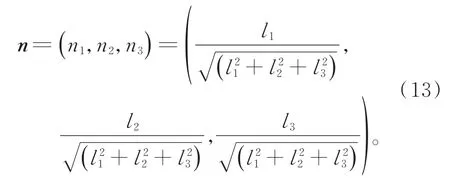
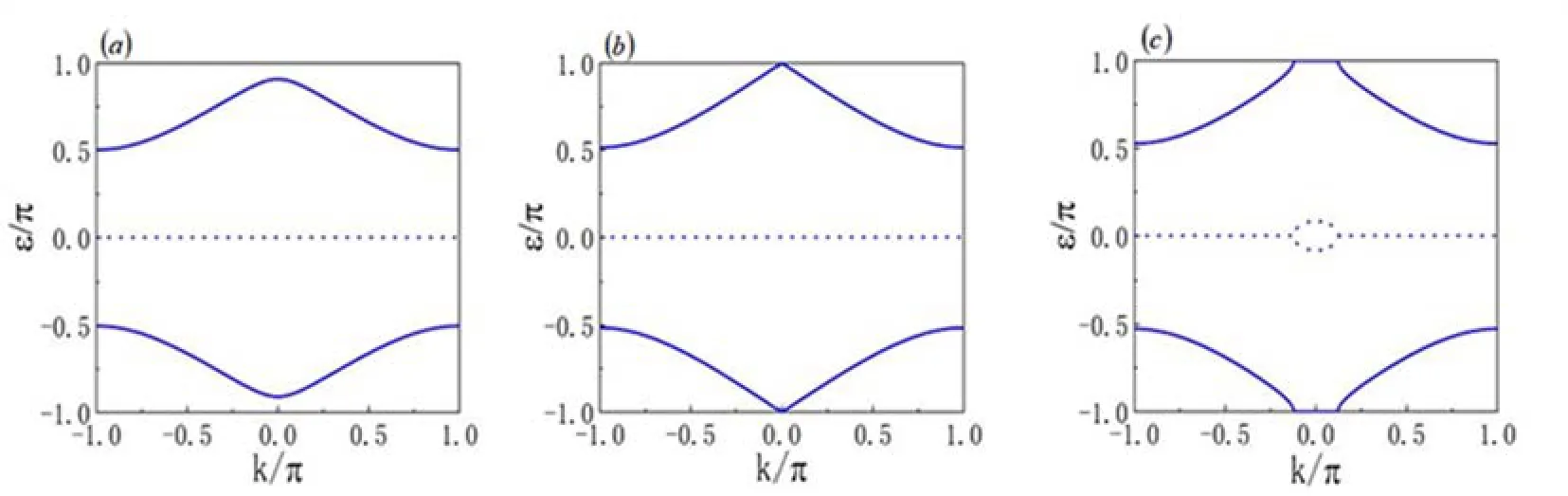
图1 准能量ε随动量k的变化图，实线代表的是准能量的实部，虚线代表的是准能量的虚部（a）τ=ln1.1，（b）τ=ln1.252，（c）τ=ln1.34Fig.1 Variation of quasi-energy εas a function of k.The solid（dashed）curves represent the real（imaginary）part of the quasienergy，（a）τ=ln1.1，（b）τ=ln1.252，（c）τ=ln1.34

有一种与手征对称相关的方法来描述量子行走中的拓扑相，就是利用Zak相位的不同值来区分拓扑的平庸相和非平庸相。Zak相位γ由极化矢量n(k)可定义为：

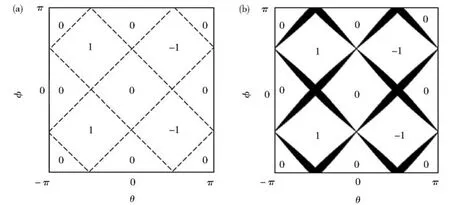
图2 量子行走在参数空间(θ，φ)的拓扑相图（a）幺正情况τ=0，（b）非幺正情况τ=0.1.图（b）中阴影部分表示PT对称自发破坏的区域Fig.2 Topological phase diagram in(θ，φ )parameter space for quantum walk.（a）the case of unitary dynamics(τ=0).（b）the case of non-unitary dynamics(τ=0.1).The shadow regions in（b）indicate the broken PT-symmetry region

当增益损耗参数τ不为零时，在参数空间(θ，φ)的不同区域，系统的准能量可能为实数，也可能为复数。在准能量为实数的区域，系统的PT对称性未破缺，由方程（15）可以计算出Zak相位，其值同样为1、0或-1，很好地描述了系统的拓扑特性。在准能量为复数的区域，系统的PT对称自发破缺，准能量的上下两支的实部在以k=0为中心点的一个范围内发生简并，能隙闭合为一条线段（如图1（c）所示），此时系统Zak相位的定义式（15）不能成立。在图2（b）给出的非幺正PT对称量子行走的拓扑相图中，阴影区域就是由于τ因子的作用，使得系统PT对称自发破缺。随着增益损耗系数τ的变大，会出现更大的阴影区域。

2 非幺正PT对称量子行走的平均位移

除了Zak相位之外，我们还可以用实验可观测量平均位移来描述量子行走的拓扑相变，这一过程是一个动力学变化过程，和Zak相位分别从动态和静态不同的角度对拓扑变化进行描述。考虑粒子初始局域在x=0位置，用处于手征算符σx本征值为1的本征态作为量子行走的初始硬币态，则量子行走的初态为

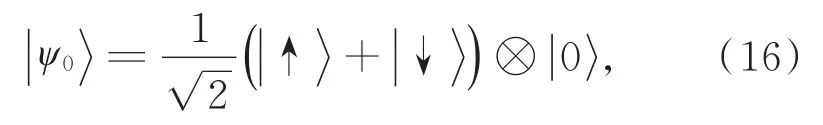
在演化算符Upt的作用下，演化t步后量子行走的状态为

相应地，t步后量子行走的平均位移为

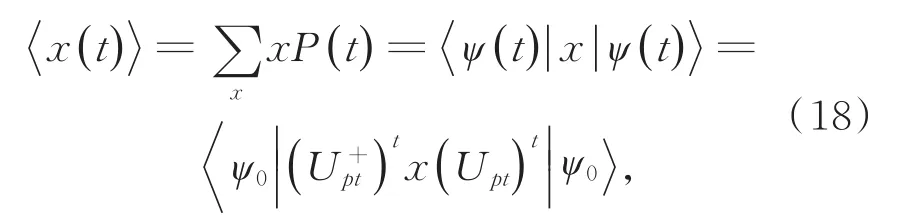
将上式作傅里叶变换，

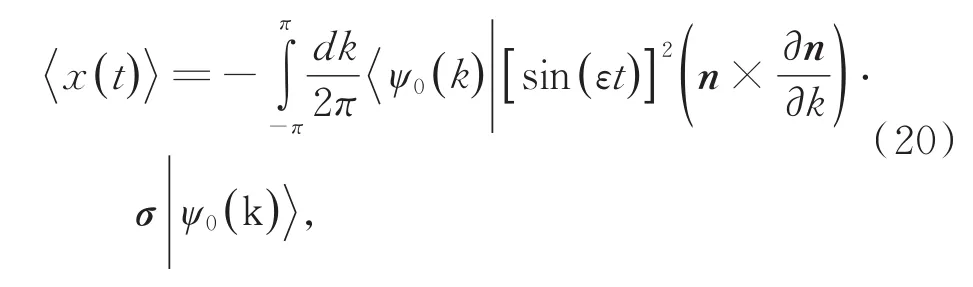
在初态方程（16）下，由于方程（20）中只有包含σx的积分项不为零，因此得到的是一个实数。同时，由于积分项中存在随t的变化会不断振荡。为此，我们求平均位移从一步演化到N步演化的平均值，以消除平均位移对t的依赖性，即有

选取N=30，图3（a）和（b）分别给出增益损耗参数τ=0和τ=0.1这两种情况下，量子行走的平均位移随参数θ的变化曲线，图中蓝色实线，红色虚线，紫色点线分别对应参数φ取π2，π4和0时的变化情况。从图3（a）中可以看出，当τ=0时，的变化与（15）式定义的Zak相位的变化相同，只是平台值的大小减少一半；当τ=0.1时，图3（b）中的红色虚线和紫色点线会出现间断现象，间断区域（用黑色圆点填充）对应的值为复数，也就是系统PT对称自发破缺所对应的参数θ取值范围；蓝色实线仍显示出随着参数θ的变化跳变的现象。这些变化特征与Zak相位在相图图2（b）中的变化完全一致，考虑到当前的实验技术可以进行测量量子行走演化后的平均位移，因此可以用平均位移来观察非幺正PT对称量子行走的拓扑相变。

图3 量子行走平均位移随参数θ的变化曲线，（a）τ=0，（b）τ=0.1蓝色实线，红色虚线和紫色点线分别对应φ=π 2，π 4和0。黑色填充圆形表示PT对称破缺的区域Fig.3 Mean position of quantum walk varies as a function of the coin parameterθ，with（a）τ=0，（b）τ=0.1.Blue solid line，red dash line and purple dotted line correspond to theφ= π 2，π 4and0，respectively.The black filled disks in（b）indicate the broken PT-symmetry region

3 结论

本文考虑系统的增益损耗效应，引入非幺正算符，将幺正量子行走推广至满足PT对称的一维非幺正量子行走。调节系统中的参数，系统的准能量可能为实数，也可能为复数，分别对应系统满足PT对称性和系统PT对称性破缺。通过计算系统的Zak相位，给出系统的拓扑变化相图。当系统满足幺正条件时，拓扑相边界是一条直线段，但当系统变为非幺正系统时，拓扑相边界变为一个个有限区域，区域的面积随着增益损耗参数的增大而变大。在这些相边界区域所对应的参数下，准能量恰好为复数，且准能量实部二重简并。计算量子行走的平均位移，发现平均位移随硬币参数的变化也可以表征系统的拓扑相变，且与由Zak相位表征的拓扑相图基本一致，为实验上通过测量动力学量来判断系统的拓扑相提供了一种有效方法。