基于离散有限元仿真技术的螺旋输砂装置研究*
2021-05-18潘灵永宋满华
潘灵永 应 杰 尹 进 宋满华
(1.中石化四机石油机械有限公司 2.中石化石油机械股份有限公司研究院)
0 引 言
螺旋输砂装置是混砂车的关键部件之一,用于满足大型加砂需求以及实现输砂量的精确计量[1-4]。深层页岩气开发的压裂工艺具有大排量、长时间连续施工等特点,其对混砂装置的功率储备范围、持续施工能力、输砂计量控制精度及动态性能等方面提出了更高要求。长期以来,理论公式被广泛应用于螺旋输砂装置的输砂能力设计计算,设计结果与试验结果存在较大差距[1]。李立等[5]通过建立螺旋输砂试验装置,从统计试验数据出发,修正了混砂车输砂能力计算公式,该方法只能适用于特定系列的输砂装置设计计算,并不能应用于螺旋输砂装置的系列化开发。刘春雪等[2]以HS210混砂车螺旋输砂器为原型,采用量纲分析法对输砂量进行了数值模拟,数值模拟结果与理论计算结果误差在22%以内,但缺少进一步的试验验证。贾宏禹等[6]通过将螺旋输砂装置简化为简支梁,利用有限元法研究了静扰度和固有频率等参数。已有的研究大多停留在螺旋输砂装置的稳态性方面,对装置本身的动态性能研究相对较少。
离散有限元仿真技术(Discrete Element Method,DEM)于20世纪70年代由P.A.CUNDALL提出,已成为研究非连续性介质问题的有效手段[7-12]。文献[11]和[13]用DEM方法模拟单螺旋叶片输送机的输送性能,并分析了安装倾角、转速以及物料填充率等参数对输送性能的影响。文献[9]和[10]研究了DEM仿真技术中颗粒直径和形状等参数对仿真结果的影响,研究结果表明,适当放大颗粒直径对计算结果影响较小。
本文从螺旋输砂装置的结构参数和操作参数出发,建立螺旋输砂装置参数模型,并确定仿真初始条件和边界条件;利用DEM仿真技术,结合Hert-Mindlin接触模型建立仿真模型,分析螺旋输砂装置静态和动态性能,以期为系列化开发螺旋输砂装置提供理论基础,并指导螺旋输砂装置控制器设计及优化。
1 螺旋输砂装置结构
现有混砂车中的螺旋输砂装置常采用双筒输送结构,与地面成45°安装倾角,螺旋叶片与螺旋中轴焊接为一体。压裂支撑砂粒或陶粒从进砂口进入绞龙壳体内,在液压马达的驱动下将砂斗中的支撑砂粒输送到距离地面一定高度的混合搅拌罐内或者混排一体化装置内[5]。图1为螺旋输砂装置结构示意图。

1—螺旋叶片;2—绞龙壳体;3—螺旋中轴。图1 螺旋输砂装置结构示意图Fig.1 Structural schematic of the spiral sand conveyor
螺旋输砂装置结构参数主要包括叶片直径、螺距、螺旋中轴轴径、螺旋叶片与壳体之间的间隙等,对应的操作参数包括转速、填充率及安装倾角等。本文以HS60混砂车用螺旋输砂装置为研究对象,主要结构参数和操作参数分别为:输砂器倾斜角45°,螺旋叶片直径218 mm,叶片螺距175 mm,螺旋中轴轴径76 mm,工作转速20~360 r/min,输砂范围150~10 000 kg/min。
2 支撑砂粒标定
压裂支撑砂粒作为一种散料体物料,不同于普通的固体、液体和气体,其主要力学特性包括泊松比、弹性模量和密度等。这些参数可直接通过查阅文献或出厂参数获得。接触碰撞模型所需的碰撞恢复系数、静摩擦因数和动摩擦因数等较难获得,本文采用堆积角的仿真结果和试验测试结果对比来标定仿真模型接触参数。
2.1 接触模型理论
离散元接触模型的选取对模拟结果的准确性有很大影响。考虑到压裂支撑砂粒含水体积分数极低,黏附力可忽略不计,且其圆度、球度均在0.8以上,可近似为理想颗粒体,因此本文使用Hertz-Mindlin(无滑移)接触模型。该接触模型将砂粒的作用力分解为接触点的法向力和切向力,通过法向力和切向力的耦合计算,可以获得颗粒间接触碰撞时受到的空间作用力,并在仿真时间内迭代计算出颗粒群的位置信息。
Hertz-Mindlin接触模型中法向力Fn、切向力Ft、法向阻尼力Cn及切向阻尼力Ct计算式如下:
(1)
Ft=-Stδt
(2)
(3)
(4)

另一方面,滚动摩擦因数在仿真计算中不可忽略,笔者通过在接触表面施加一个力矩τ来考虑滚动摩擦因数,于是有:
τ=μrFnXω
(5)
式中:μr为滚动摩擦因数;X为接触点与质心之间的距离,m;ω为物体接触点处的单位角速度,rad/s。
2.2 支撑砂粒堆积角仿真分析
由于支撑砂粒粒径较小,以物理试验用20/40目石英砂为例,其最大粒径约为0.85 mm。为进一步提高计算效率,并结合文献[10]的研究结果,本文将支撑砂粒平均直径放大至5 mm。仿真试验模型由圆筒和其下方的基板组成,测试圆筒结构参数,其直径为50 mm,高度为250 mm。天然石英砂初始堆积在圆筒中,料筒以缓慢的速度垂直于料板提升,堆积过程模拟如图2所示。

图2 支撑砂粒堆积过程模拟图Fig.2 Simulation diagram of sand stacking process
在Hertz-Mindlin模型中,颗粒间的静摩擦因数和滚动摩擦因数是影响颗粒堆积角的重要因素[14]。图3~图5表示不同静摩擦因数下支撑砂粒的堆积角特性。
由图3和图5可知:当颗粒-颗粒的滚动摩擦因数(取0.05)和恢复系数等其他物性参数相同时,颗粒的堆积势能随静摩擦因数的增大而增大,最终趋于定值;另一方面,堆积角随静摩擦因数的增大而增大。
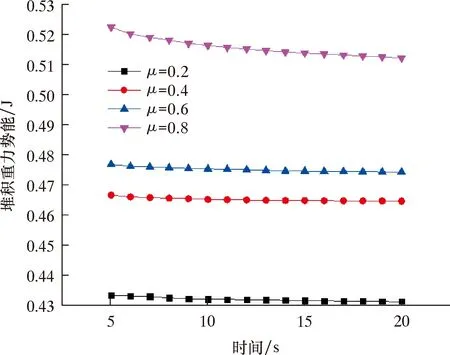
图3 不同静摩擦因数对应的堆积重力势能Fig.3 Stacking gravity potential energy corresponding to different static friction factors

图4 不同静摩擦因数下的颗粒堆积状态Fig.4 Particle stacking state under different static friction factors
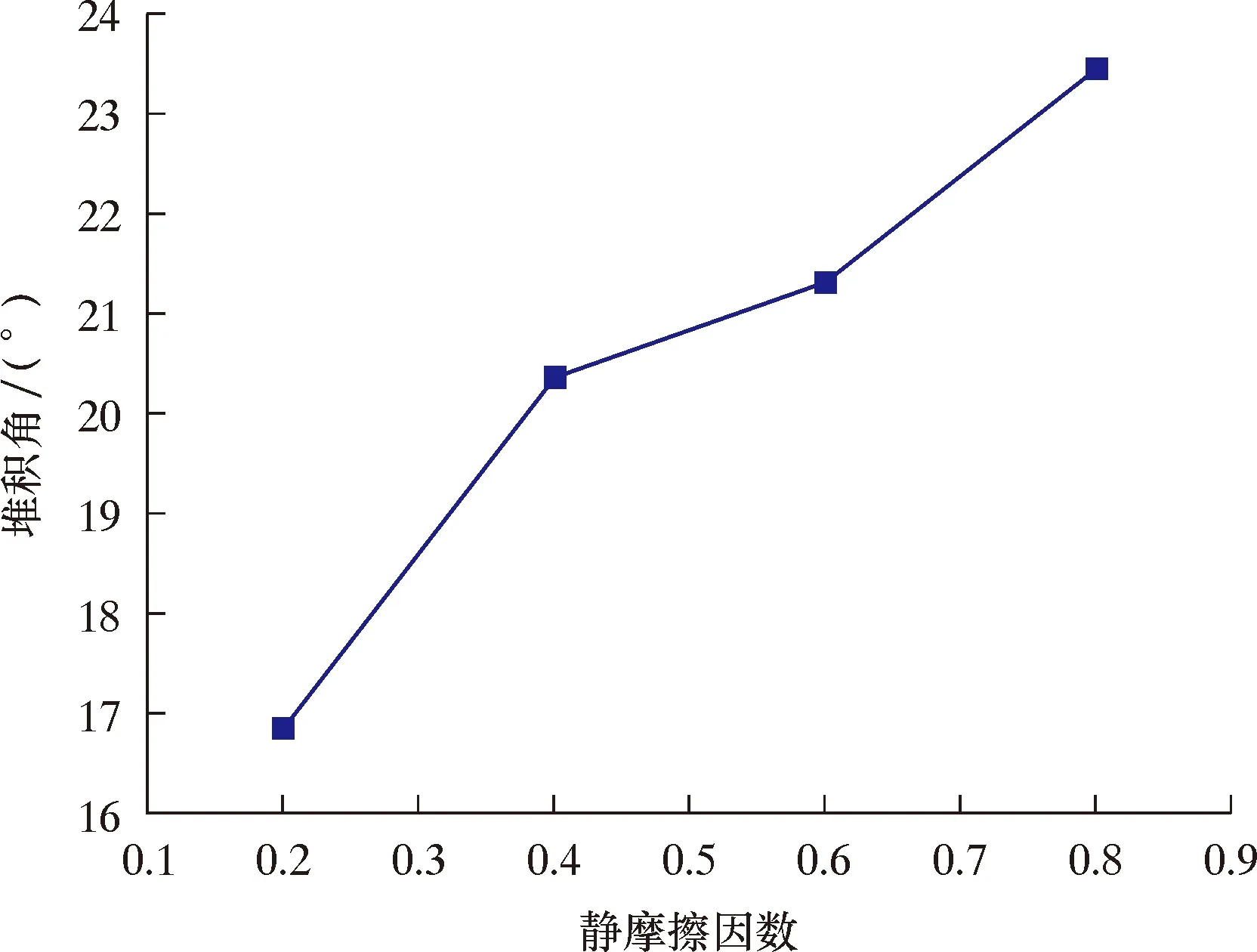
图5 不同静摩擦因数对应的堆积角Fig.5 Stacking angle corresponding to different static friction factors
图6~图8表示不同滚动摩擦因素下支撑砂粒的堆积角特性。由图7和图8可知,当颗粒-颗粒的静摩擦因数(取0.6)和恢复系数等其他物性参数相同时,颗粒-颗粒之间滚动摩擦因数的增大会抑制颗粒间的相对滚动,从而使颗粒堆积角增大,且影响比静摩擦因数的影响要大。这是因为在堆积过程中颗粒的主要运动形式是滚动,且当颗粒-颗粒静摩擦因数和滚动摩擦因数均较大时,颗粒堆就容易呈现出凹、凸等不规则外形。

图6 不同滚动摩擦因数下的颗粒堆积状态Fig.6 Particle stacking state under different rolling friction factors

图7 不同滚动摩擦因数下的堆积重力势能Fig.7 Stacking gravity potential energy under different rolling friction factors
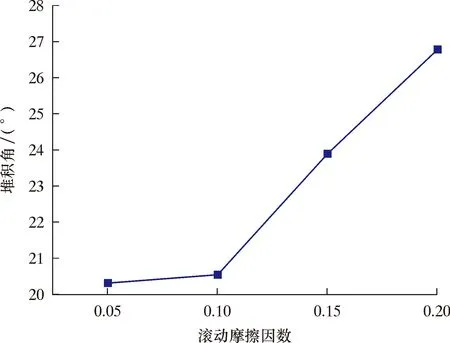
图8 不同滚动摩擦因数下的堆积角Fig.8 Stacking angle under different rolling friction factors
2.3 支撑砂粒堆积试验及仿真模型标定
为了获得准确的仿真参数,采用堆积角模拟仿真与试验验证相结合的方式。室内支撑砂粒堆积角测试获得的平均堆积角为23.38°。通过调整仿真参数,并经过3次重复仿真,得到的堆积角分别为22.66°、24.27°和23.09°,均值为23.34°。堆积角试验结果和仿真结果对比如图9所示。
最终标定的支撑砂粒接触参数分别为:颗粒-颗粒恢复系数0.4,颗粒-颗粒静摩擦因数0.4,颗粒-颗粒滚动摩擦因数0.15,颗粒-料板恢复系数0.5,颗粒-料板静摩擦因数0.4,颗粒-料板滚动摩擦因数0.05。

图9 支撑砂粒堆积角试验结果及模拟结果对比图Fig.9 Comparison of test results and simulation results of sand stacking angle
3 螺旋输砂装置性能仿真
笔者建立的HS360螺旋输砂装置仿真模型如图10所示。为研究不同转速下螺旋输砂装置的输砂量和填充率,螺旋输砂器静态特性分析主要研究不同转速下混砂装置的输砂量和填充率。在仿真模型中将转速范围设定在5~400 r/min,转速与输砂量之间的关系曲线如图11所示。
由图11可知:当转速在10~300 r/min时,转速与输砂量基本呈线性关系;随着转速的进一步增大,输砂量基本趋于平稳。图12为螺旋输砂装置转速与填充率的关系曲线。由图12可知,填充率与螺旋输砂装置转速基本呈线性关系,且随转速的增加而减小。

图10 螺旋输砂装置仿真模型Fig.10 Simulation model for spiral sand conveyor

图11 螺旋输砂装置转速与输砂量的关系曲线Fig.11 The relationship between the speed of the spiral sand conveyor and the sand conveying volume

图12 螺旋输砂装置转速与填充率的关系曲线Fig.12 The relationship between the speed of the spiral sand conveyor and the filling rate
分析其原因,当螺旋输砂装置转速过高时,一方面会增强螺旋输砂装置壳体的振动、降低支撑轴承密封性能;另一方面,由于螺旋输砂装置存在45°的安装倾角,随着转速的增大,支撑砂粒物料相对于螺旋叶片的切向速度增大,而支撑砂粒与螺旋叶片及壳体的摩擦因数固定,从而使支撑砂粒填充率降低。因此,额定转速应控制在10~350 r/min范围内,这一转速与实际工程相接近。
图13为螺旋输砂装置启动后到出砂口平稳出料时延迟时间与转速的关系曲线。
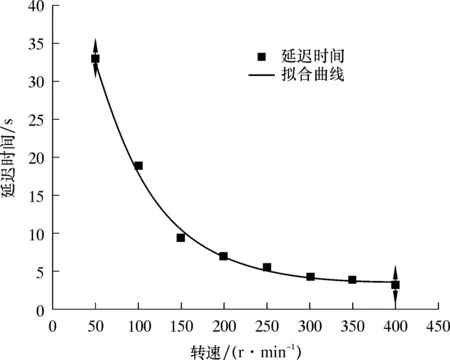
图13 螺旋输砂装置转速与平稳出料延迟时间的关系曲线Fig.13 The relationship between the speed of the spiral sand conveyor and the delay time of steady discharge
由图13可知,延迟时间随转速的增大而缩短,且延迟时间与转速近似呈指数关系,其拟合曲线方程如下:
t=3.284 64-60.484 54×0.986n
(6)
式中:t为延迟时间,s;n为转速,r/min。
式(6)也体现了螺旋输砂装置的动态特性,可为控制器设计提供指导。
为进一步研究螺旋输砂装置叶片螺距P对输砂量和平稳出料时间的影响,在保持叶片直径D不变的前提下,分别模拟P/D=0.5、0.8和1.0几种不同螺距的螺旋输砂装置性能。其中,P/D=0.8为现有结构。
图14为转速300 r/min时,不同螺距下的输砂量瞬时曲线。由图14可知,螺距越大,延迟时间越短,但稳态输砂量波动越大,而且螺距对平均输砂量影响不大。因此,在保证螺旋叶片结构强度的前提下,合理优化螺旋叶片螺距是保证平稳输砂性能的关键。
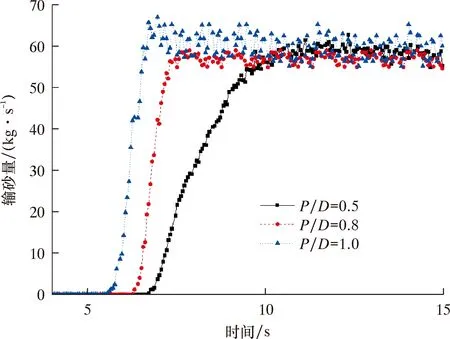
图14 螺旋输砂装置螺距与出料的时间曲线Fig.14 The screw pitch and discharge time curve of the spiral sand conveyor
4 结 论
(1)通过试验和仿真模拟,标定了模型的接触参数。试验结果发现,随着颗粒-颗粒的静摩擦因数和动摩擦因数的增大,堆积角度呈增大趋势,且颗粒-颗粒的动摩擦因数比静摩擦因数的影响大。
(2)通过性能仿真发现,填充率与转速基本呈线性关系,且随转速的增大而减小。随着转速的提高,支撑砂粒物料相对于螺旋叶片的切向速度增大,而支撑砂粒与螺旋叶片及壳体的摩擦因数固定,从而使支撑砂粒填充率降低。同时在保证螺旋叶片结构强度的前提下,合理优化螺旋叶片螺距是保证平稳输砂性能的关键。
