广义二型模糊逻辑系统降型及其采样离散Nie-Tan算法*

陈 阳，王 涛

(辽宁工业大学理学院,辽宁 锦州 121001)

1 引言

由于区间二型模糊逻辑系统[1 - 4]的计算复杂度相对较低，已成为当前应用最广泛的一类二型模糊逻辑系统。自从广义二型模糊集的α-平面(或z切片)表达理论[5,6]被提出，广义二型模糊逻辑系统的计算量减少了，学术界对于区间二型模糊逻辑系统的众多关注逐渐转向了广义二型模糊逻辑系统[7 - 10]。区间二型模糊集的次隶属度值恒等于1，而广义二型模糊集的次隶属度值介于0和1 之间，即广义二型模糊集以非均匀方式度量隶属函数不确定性。因此，广义二型模糊集可看成是比区间二型模糊集更高阶的不确定模型。随着设计自由度增加，基于广义二型模糊集的广义二型模糊逻辑系统设计在处理某些不确定性问题时具有更大的潜力。

一般来说，二型模糊逻辑系统由模糊器、推理机、规则库、降型器和解模糊器5个模块组成。首先，二型模糊输入集在推理机的指导下被转变成二型模糊输出集。接着，降型核心模块把二型模糊集转化成一型模糊集。最后解模糊化把一型模糊集映射成明确输出。当前，计算密集的KM(Karnik-Mendel)类算法[11 - 15]仍是最流行的降型算法。为了改进计算效率，一些非迭代类算法被陆续提出，如NT(Nie-Tan)算法[16]、BMM(Begian-Melek-Mendel)算法[17]、NB(Nagar-Bardini)算法[18,19]、CJ(Coupland-John)算法[20]和GCCD(Greenfield-Chiclana Collapsing Defuzzifier)算法[21]]等。其中NT算法具有简单的闭环形式，且连续NT算法CNT(Continuous NT)在最新的研究中被证明为准确的计算区间二型模糊集质心的方法。

本文以CNT算法为计算基准，提出基于采样的离散NT算法来实现广义二型模糊逻辑系统质心降型和解模糊化。证明了当适当选取质心输出广义二型模糊集的主变量采样点个数时，离散NT算法的计算结果可以精确地逼近CNT算法的计算结果。 本文的余下部分组织如下：第2节简要介绍广义二型模糊逻辑系统；第3节给出NT和CNT算法，以及如何用它们来实现广义二型模糊逻辑系统质心降型和解模糊化；第4节采用数值仿真例子比较和分析采样离散NT算法的表现；最后给出结论与展望。

2 广义二型模糊逻辑系统

从推理结构的角度看，广义二型模糊逻辑系统一般可分为Mamdani型[4,8,13]和TSK(Takagi-Sugeno-Kang)型[1,9]。本文只关注Mamdani型的质心降型研究。不失一般性，考虑一个有n个输入x1∈X1,…,xn∈Xn和1个输出y∈Y的Mamdani型广义二型模糊逻辑系统，该系统由M条模糊规则描述，且其中第s条规则形式为：

(1)

(2)

对于每条模糊规则，在指定α水平下的激发区间为：

(3)

其中,T表示取小或乘积t-范[6],p为前件个数。

(4)

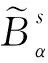
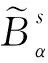
(5)

(6)

(7)

(8)

最后聚合所有的α-平面YC,α来构成一型模糊集YC,即:

(9)

3 NT和CNT算法

(10)

聚合所有的YNT,α得出一型模糊集YNT,即:

(11)

在实际计算中,假设有效α-平面的个数为m,即把α值均匀分解成α1,α2,…,αm,那么广义二型模糊逻辑系统的输出为:

(12)

最新的研究证明了CNT算法[16]是计算区间二型模糊集质心的准确方法。这里给出解释并将其推广成计算广义二型模糊逻辑系统质心。

定理1[16]当采样点个数趋于无穷时，随机采样方法可准确地完成广义二型模糊逻辑系统质心降型。

(13)

其中，yj是y的离散切片。

所以，

(14)

(15)

所以，

(16)

(17)

□

(18)

(19)

(20)

其中ωi是一个均匀分布在[0，1]上的随机数,所以可得：

(21)

(22)

当前流行的解模糊化一型模糊集方法是计算其质心，即：

(23)

既然yj是任意一块垂直切片，式(22)对所有的y都成立,因此可得:

(24)

□

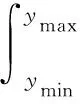
(25)

广义二型模糊逻辑系统的降型集和解模糊化值可分别由式(11)和式(12)计算得出。

最后对于CNT和采样离散NT算法实现广义二型模糊逻辑系统质心降型作出如下总结：

(1) 离散NT算法是基于采样点的求和运算完成质心降型，而CNT算法以求积分运算完成质心降型。从理论上说，当采样点个数N→∞时，NT算法的计算结果会趋于CNT算法的计算结果。

(2) 随着采样点个数的增加,NT算法可能会取得更准确的计算结果。

(3) 离散NT算法是以求和运算完成数值计算的,而CNT算法是以求积分运算象征性地完成计算。

4 仿真实验

本节给出3个计算机仿真示例。通过模糊推理，设广义二型模糊逻辑系统的质心输出二型模糊集的足迹不确定性FOU(Footprint Of Uncertainty)和相关次隶属函数(或称垂直切片)为已知量。这里取二型学术研究中常见的3个广义二型模糊集。在例1中，FOU是由分段线性函数[13 - 16]限定，相关垂直切片为梯形隶属函数。在例2中,FOU是由线性函数和高斯函数混合[17-21]限定,相关次隶属函数仍为梯形函数。在例3中，FOU由高斯函数[13 - 16]限定，相关垂直切片为三角形隶属函数。实验中α被均匀分解成Δ个有效值，即α=0,1/Δ,…,(Δ-1)/Δ,1。取Δ以1为步长从1到100变化。

图1和表1给出了所定义的FOU,图2和表2给出了所定义的次隶属函数。

Figure 1 Graphs of FOU图1 FOU图

Table 1 Membership function expressions for FOU

Figure 2 Shape of vertical slices图2 垂直切片形状

Table 2 Expressions for secondary membership functions

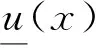
Figure 3 Centroid type-reduced sets computed by CNT algorithm图3 CNT算法计算出的质心降型集

Figure 4 Defuzzified values computed by CNT algorithm图4 CNT算法计算出的解模糊化值

实验中研究离散NT算法与基准的CNT算法之间的关系，当取前者的主变量采样个数为20，50，100，200和2 000时，CNT算法和离散NT算法计算出的质心降型集绝对误差如图5所示。

CNT算法和NT算法计算出的解模糊化值绝对误差在图6中给出。

Figure 5 Absolute errors of cancroids type-reduced sets between CNT and NT algorithms图5 CNT和NT算法计算出的质心降型集绝对误差

Figure 6 Absolute errors of defuzzified values between CNT and NT algorithms图6 CNT和NT算法计算出的解模糊化值绝对误差

接着定量研究绝对误差的平均值，这里取计算精度为10-4。当有效α-平面个数Δ=100时，表3给出了基准CNT算法和离散NT算法计算出的质心降型集绝对误差平均值。

当Δ=1∶1∶100时，CNT算法和离散NT算法计算出的降型集绝对误差在表4中给出。

接下来研究CNT算法和采样离散NT算法的具体计算时间。仿真平台为有E5300@2.60 GHz，2.00 GB内存的双核戴尔台式机，操作系统为Windows XP。所有算法均由Matlab 2013a编程。计算质心降型集和解模糊化时的时间如表5和表6所示。

Table 3 Averages of absolute errors of centroid type-reduced sets表3 质心降型集绝对误差平均数

Table 4 Averages of absolute errors of defuzzified values表4 解模糊化值绝对误差平均数

观察图5、图6和表3～表6，可以得出以下结论：

(1) 随着主变量采样点个数增加，无论是计算广义二型模糊逻辑系统质心降型集或还是解模糊化值，离散NT算法的结果都会越来越接近基准CNT算法的结果。

(2) 在例1中，只需取采样点个数为100和20,离散NT算法的计算结果就同CNT算法一样(见图5a和图6a)；而在例2和例3中，需要增加采样点个数到2 000才能使离散NT算法的计算结果与CNT算法的结果相同 (见图5b、图5c、图6b和图6c)。

Table 5 Computation time of centroid type-reduced sets表5 质心降型集计算时间 s

Table 6 Computation time of defuzzified values表6 解模糊化值计算时间 s

(3) 当考虑计算质心降型集和解模糊化值绝对误差平均数时，则需要把采样点个数增加到35 000才能使这3个例子下的离散NT算法计算时精确逼近CNT算法。

(4) 对于质心降型集和解模糊化值的具体计算时间，本文所提出的采样离散NT算法的计算用时远远少于CNT算法的。其中采样数最多的离散NT算法所需计算时间最长。尽管如此，计算用时最长的离散NT算法仅仅需要1.617 1%的CNT算法的计算时间。

(5) 综合以上4条分析，可知采样离散NT算法是优秀的CNT算法的估计方法。此外，采样离散NT算法的计算效率远高于CNT算法的。

5 结束语

本文揭示了离散NT算法和连续NT(CNT)算法的内在联系，证明了CNT算法可实现准确的广义二型模糊逻辑系统质心降型。对于3个具有不同FOU的系统输出广义二型模糊集，仿真实验表明，当适当选取推理输出广义二型模糊集主变量采样点个数时，离散NT算法得出的质心降型集和解模糊化值结果可精确地逼近CNT算法，且前者计算效率远高于后者。

在后续工作中，将研究离散降型算法和连续降型算法的关系、采样离散非迭代算法及合理初始化改进Karnik-Mendel迭代算法以实现二型模糊逻辑系统中心集降型。此外，还将深入研究基于优化算法的Begian-Melek-Mendel、Nie-Tan和Nagar-Bardini等框架结构下二型模糊逻辑系统的设计与应用。