面向FT-M7002的高斯滤波算法优化实现*

陈 云，王梦园，柴晓楠，商建东

(1.郑州大学信息工程学院，河南 郑州 450001;2.河南省超级计算中心(郑州大学),河南 郑州 450052)

1 引言

DSP(Digital Signal Processor)起源于20世纪70年代，针对数字信号处理中存在的大量累加累乘运算设置乘加器MAC(Multiplication Adder Cycle)部件，结构比较简单。随着社会的不断进步，DSP的应用领域也变得更加广泛，为满足大型稠密线性方程组求解、雷达信号处理、高清视频和数字图像处理等计算密集型应用的高性能计算需求,数字信号处理器的体系结构出现显著变化,出现了高性能数字信号处理器。目前应用较多的高性能DSP体系结构主要有片上多核以及核内集成支持了单指令多数据SIMD(Single Instruction Multiple Data)、超长指令字VLIW(Very Long Instruction Word)技术的部件， 比如TI的TMS320C6678处理器，片上集成8个DSP核心，单核浮点运算能力可达20 GFlop/s[1,2]。近几年我国高性能数字信号处理器的研究也取得了一定的成就，国防科技大学自主研发的飞腾FT(FeiTeng)系列多核处理器[3]、向量处理器相继出现。但是,硬件的快速发展也会带来一些问题，如缺乏配套的软件应用，只有适配相应的软件应用才能充分发挥高性能DSP的特殊硬件架构优势，实现国产数字信号处理器在图像处理、雷达信号处理等领域的实时性与高效性。因此，基于快速发展的我国高性能数字信号处理器，开发相应的高性能软件应用是我们需要考虑并解决的问题。

在图像处理领域，一般待处理图像中往往会存在一定程度的噪声干扰，恶化了图像的质量。高斯平滑滤波作为图像预处理的重要组成部分具有优良的噪声平滑性能和边缘保留能力[4,5]，是保证后续特征提取与识别正确进行的基础。现有的高斯滤波算法实现并不能充分利用FT平台的计算性能，会影响到使用该算法的多种大型图像处理应用，因此面向FT系列处理器实现高效的高斯滤波算法具有重要的意义。

目前有很多学者针对硬件特性对高斯滤波算法进行相应的优化，并取得了一定成果。文献[6]针对TMS320C6x系列处理器提出了一种单次遍历实现2次卷积的高斯平滑滤波DSP优化方法；文献[7]针对TMS320C6416处理器的内部资源，提出了基于该处理器的空间低通滤波程序的设计方案；文献[8]基于CPU的SSE指令集，完成了高斯滤波器的SIMD优化递归IIR(Infinite Impulse Response)实现，并在OpenMP(Open Multi- Processing)的帮助下实现了单指令多数据扩展流SSE(Streaming SIMD Extensions)版本的并行化;文献[9]总结了高斯滤波算法原理和CUDA(Compute Unified Device Architecture)并行计算体系,提出了适合于CUDA的并行高斯滤波算法。但是,由于不同处理器体系结构的差异性，上述并行优化算法并不适用于FT系列高性能数字信号处理平台。

本文面向国防科技大学自主研发的FT-M7002高性能处理器的特殊硬件架构，设计高斯滤波并行算法。主要内容包含以下几个方面：(1)分析高斯滤波算法计算特点与FT-M7002体系结构；(2)分析高斯滤波算法加速瓶颈，设计相应的优化方案；(3)通过手工向量化、控制流消除和循环展开等优化手段充分利用数据级与指令级并行性；(4)针对FT-MT2内核中的DMA(Direct Memory Access)硬件和向量存储器结构特点，进行了“乒-乓”缓存、DMA数组转置等优化。

2 高斯滤波算法

2.1 滤波

高斯滤波广泛应用于减弱图像中的高斯噪声，其计算过程就是对一幅图像进行加权平均的过程，每一个结果像素点的值都由相应输入图像像素值与滤波核矩阵进行相乘并累加后得到。令I是大小为m*n的输入图像矩阵，G(u,v)为高斯函数，O为输出结果矩阵，则滤波过程定义如式(1)所示：

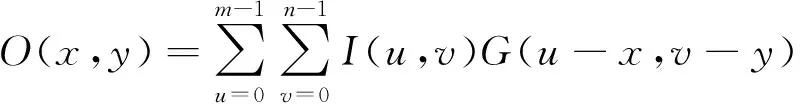
(1)

针对本文高斯滤波，G(u,v)定义如式(2)所示：

(2)

其中，u0和v0是均值，代表中心点坐标，一般取值为0;δ2是方差，代表高斯曲线的宽度[10,11]。

滤波就是对输入图像进行模糊的过程，可以理解成每一个像素点的值都用其周边像素点的值的加权平均值代替。中间像素点的值用周围像素点的值的平均值代替，中间像素点的值取周围像素点的值的均值代替，会使中间像素点失去细节，图像上就会产生模糊效果。但是，在计算过程中存在周围像素权重分配的问题，如果使用简单的平均显然是不合理的，因为图像都是连续的，越靠近中间点的像素与中间点的相关性越强。因此，加权平均的计算方式更合理，距离中心点越近的像素点权重越大，距离中心点越远的像素点权重越小。由于高斯分布在形状上是一种钟形曲线，因此高斯分布是一种可取的权重分配模式。

2.2 高斯滤波算法的实现方法分析

在目前常用的图像处理库中，高斯滤波一般有2种实现方式，一种是借助快速傅里叶变换FFT(Fast Fourier Transform)实现，一种是使用离散化高斯窗口在原图像上进行滑动卷积。基于快速傅里叶变换的高斯滤波实现如图1所示，分别将输入图像矩阵和滤波核矩阵进行二维FFT计算，根据时域计算与频域计算的对应关系，可将时域中的卷积计算转换成频域中的复乘运算，最后通过二维逆傅里叶变换得到最终的结果矩阵。该方法的优点是计算量与卷积核的大小无关，因此针对卷积核尺寸较大的卷积网络，FFT方法相比直接卷积方法在降低计算量方面具有明显的优势，其不足之处就是要付出增加存储开销的代价[11]。但是，一般滤波采用的卷积核尺寸都比较小，因此可以选择使用离散化高斯窗口在原图像上进行滑动卷积的方式实现高斯滤波。

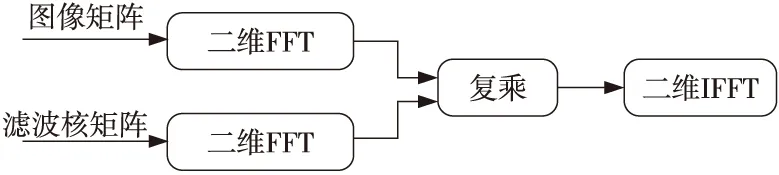
Figure 1 Gaussian filtering implementation based on Fourier transform图1 基于傅里叶变换的高斯滤波实现

通过离散化高斯窗口在原图像上进行滑动卷积时，先通过二维高斯函数生成二维高斯核，移动高斯核，将该高斯核与输入图像的相应位置像素点相乘累加得到相应位置的滤波结果。图2给出了使用3*3高斯核进行滑动卷积的示意图，在计算像素点I(1,1)滤波结果时，用高斯滤波核G覆盖以像素点I(1,1)为中心点的3*3图像区域，高斯核G与图像区域内相对应的像素点数据相乘并累加，便可得到I(1,1)像素点的高斯滤波处理结果O(1,1)。计算I(1,2)像素点时，将高斯核G向右移一个像素的位置并重复上面的计算过程。

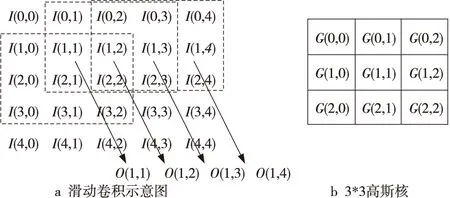
Figure 2 Schematic diagram of 3*3 Gaussian kernel sliding convolution图2 3*3高斯核滑动卷积示意图

根据高斯函数的性质，二维高斯函数可以写成2个一维高斯函数相乘的形式，因此可以采用可分离滤波器来实现高斯滤波的加速计算。所谓的可分离滤波器，就是把多维卷积转换成多个一维卷积，二维的高斯滤波就是指先对行做一维卷积，再对列做一维卷积。

定义一维高斯函数为G(u)，则:

(3)

根据式(2)中二维高斯函数的定义，可得：

(4)

根据式(4)，对式(1)中的卷积计算进行改写：

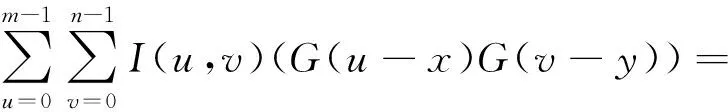
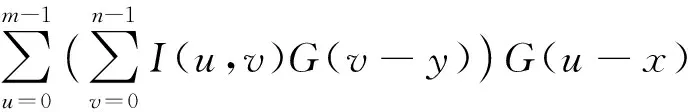
(5)

式(5)说明了高斯滤波的可分离特性，输入图像矩阵与二维高斯滤波核卷积等价于先对输入矩阵在水平方向与一维行高斯核进行卷积，再将卷积结果在垂直方向与一维列高斯核进行卷积。相对于二维滑动卷积该实现方法可以明显降低算法复杂度，在数据访问中，分离滤波可以更好地实现数据的连续访存，提高数据局部性。因此，本文将基于FT系列处理器在分离滤波的基础上实现高斯滤波的并行计算。

3 FT高性能DSP处理器

FT-M7002是国防科技大学自主研发的一款40 nm工艺的高性能DSP处理器芯片,该芯片包含1个RISC CPU核和2个FT-MT2 DSP核。单个计算核拥有32 KB的一级数据缓存和512 KB的阵列存储器AM(Array Memory)空间，核外拥有32 GB的大容量DDR存储空间[12,13]，在图像处理等需要进行大量数据运算的场合下能很好地发挥其优势，或嵌入到其他系统中作为信号协处理模块。本文主要针对单个DSP核进行算法实现，因此主要关注单个核内结构。

FT-MT2内核基于VLIW结构，具体结构如图3所示,SPU(Scalar Processing Unit)表示标量处理部件，VPU(Vector Processing Unit)表示向量处理部件，SVR(Scalar Vector Register)表示标向量共享寄存器，SPE(Scalar Processing Element)表示标量处理单元，SM(Scalar Memory)表示标量存储器。在该内核结构中，SPU和VPU为相互独立又相互关联的处理部件，SPU负责控制和逻辑计算，VPU主要面向密集型计算，SPU和VPU可以通过SVR进行数据交互，并且通过广播操作支持标量寄存器到向量寄存器的广播操作。

向量处理部件(VPU)由16个同构向量处理单元VPE(Vector Processing Element)和混洗/归约部件构成[14]，VPE内部集成4个运算部件用于支持标量定点和浮点运算。AM作为向量数据存储器，为VPU提供向量数据，同时AM可通过DMA与核外存储空间进行数据交互。也就是说该VPU可以同时对16路32位数据进行向量运算，并且支持混洗/规约操作，针对数据密集型运算能大量减少数据访存次数，提高运算效率。

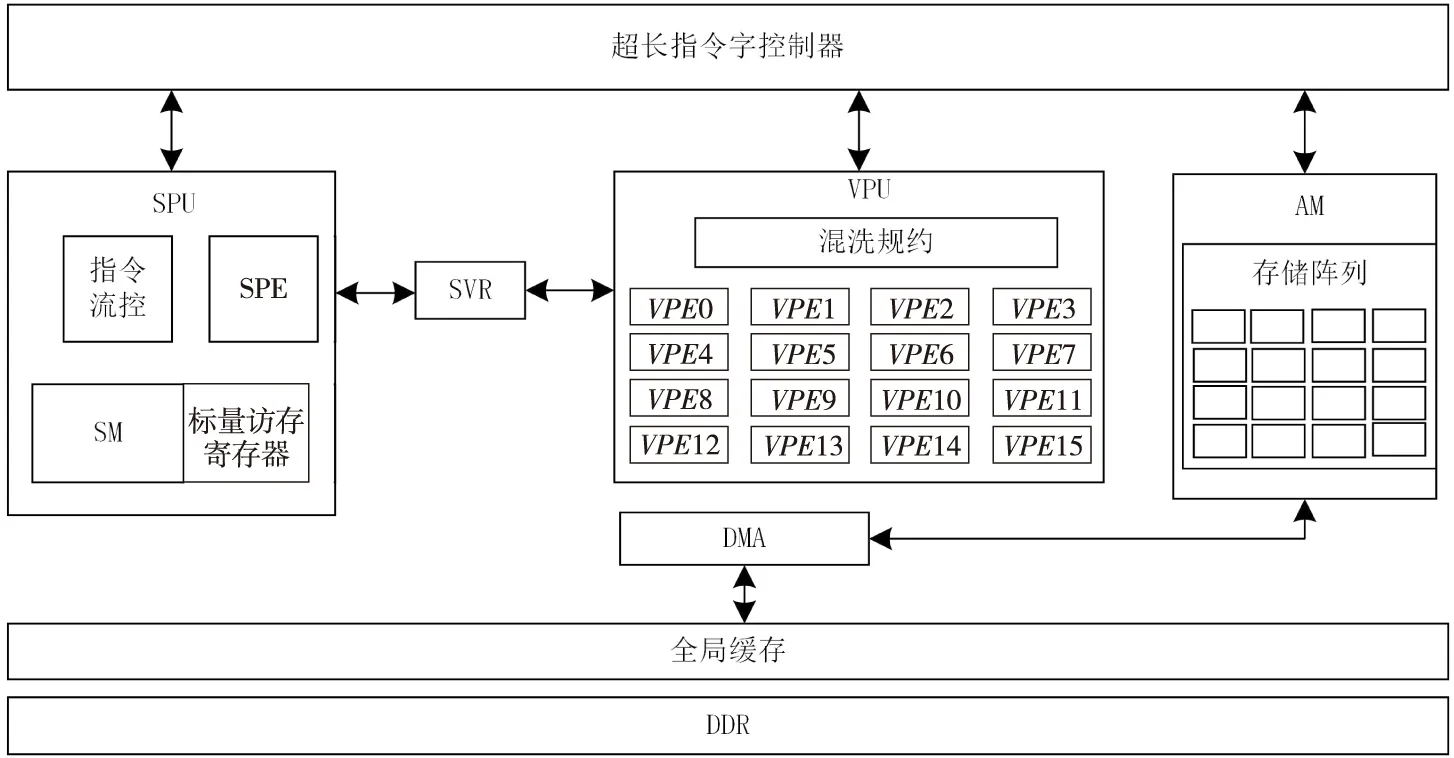
Figure 3 FT-MT2 core structure图3 FT-MT2内核结构

4 面向FT-M7002的高斯滤波算法优化实现

在分析了FT-M7002体系结构之后，本文结合该向量处理器内核特点与高斯滤波算法性能瓶颈，针对高斯滤波中密集数据访问设计了优化实现，能够明显减少访存次数，最后为进一步提升算法性能设计了相应的数据传输优化。

4.1 高斯滤波在FT平台上的优化实现

与二维高斯核滑动卷积计算高斯滤波相比，分离滤波器能够减少计算量，提高访存的局部性，但是当输入图像较大时，内存访问量依然很大，影响算法性能。因此，本文结合FT-M7002体系结构特点，设计一种基于分离滤波器的高斯滤波优化实现过程，通过充分利用FT-MT2内核中的VPU减少内存访问次数，在保证正确性的基础上提高高斯滤波算法性能。

高斯滤波算法主要由生成高斯卷积核、边界填充、行滤波、列滤波4部分构成，其中行滤波和列滤波部分存在大量密集数据访问，因此本文主要针对这2部分进行优化实现。本文对于列滤波的访存不连续进行相应的DMA数据转置优化，此外针对算法中DMA传输耗时进行了相应的优化设计。

根据图3中FT-M7002内核结构可知，VPE从AM中读取数据进行运算，比如vec_ld向量指令，从AM中连续加载16个32位数据放在VPE0～VPE15中，而SM主要为标量操作提供数据支持。在高斯滤波中，一般来说高斯核矩阵的规模都比较小，而且根据算法的需要，高斯核数据需要标量读取，因此将高斯核数据置于SM中，输入矩阵置于AM或DDR中。针对行列滤波部分，图4给出了3*3高斯核与输入图像矩阵进行滤波操作示意图，其中，I表示输入图像矩阵，cn表示输入图像通道数，G表示高斯滤波核矩阵。通过FT-M7002向量指令分别从AM按行加载16个输入矩阵数据，从SM中广播对应高斯核数据到VPE中进行向量乘加运算，可以看到该方法可以明显减少访存次数，且充分复用已取数据。

Figure 4 Schematic diagram of 3*3 Gaussian kernel line filtering optimization图4 3*3高斯核行滤波优化实现示意图

4.2 向量并行优化

基于可分离滤波器的高斯滤波主要由生成高斯卷积核、边界填充、行滤波和列滤波4部分构成，经过分析高斯滤波算法主要循环层都在行列滤波部分，因此本文主要对行列滤波部分进行并行性优化。结合FT-M7002体系结构特点，为充分利用核内VPU，减少访存操作，本文采用FT-M7002向量指令集完成行滤波操作，可以有效地并行开发程序，提高数据集并行性。下面给出了行列滤波中核心段优化代码，相对于串行程序，该优化代码一次循环可以处理16个数据，明显减少内层循环次数。其中，cn代表输入图像通道数，当输入图像尺寸不是16的倍数时需要增加尾循环。当滤波核较小时可将其全部广播到VPE中完成与输入矩阵的乘加操作，当滤波核较大时，需要增加一层循环来控制广播到VPE中的卷积核，会增加整个算法的时间，由于高斯滤波常用3*3,5*5高斯核，因此将不同尺寸高斯核分开可提升较小高斯核计算性能。

before

fori=0:1:row

forj=0:1:col*cn

S0=0;

g=j;

fork=0:1:ksize

S0 +=G[k]*I[i][g];

g+=cn;

endfor

O[i][j]=S0;

endfor

endfor

input:输入矩阵I。

output:结果矩阵O。

after

ifksizeis 3 or 5 or 7, for exampleksizeis 3

vectorG(1)=vec_svbcast(G(1))； /*Broadcast Gaussian core to VPE*/

vectorG(2)=vec_svbcast(G(2))； /*Broadcast Gaussian core to VPE*/

vectorG(3)=vec_svbcast(G(3))； /*Broadcast Gaussian core to VPE*/

fori=0:1:row

M7002_vector int *I_cn= (M7002_vector int *)0x040000000; /*Define pointer to AM*/

M7002_vector int *O_cn= (M7002_vector int *)0x040040000;

M7002_datatrans_cv(I,I_cn，(col+ksize) * 4); /*DMA transfer input matrixIto AM*/

forj1=0:16:col*cn-16 //parallel for data

vectorI1=vec_ld(j1,I_cn)；

vectorI2=vec_ld(j1+cn,I_cn)；

vectorI3=vec_ld(j1+2cn,I_cn)；

vectorO1=vec_mul(vectorG(1),vectorI1)；

vectorO2=vec_mul(vectorG(2),vectorI2)；

vectorO3=vec_mul(vectorG(3),vectorI3)；

vectorO=vec_add(vectorO1,vec_add(vectorO2,vectorO3))；

vec_st(vectorO,j1,O_cn)；

endfor

M7002_datatrans_cv(O_cn,O,j1);

forj2=j1:1:col*cn/*ifcol%16 !=0*/

O(i,j2)=G(1)*I(i,j2)+G(2)*I(i,j2+cn)*G(3)*I(i,j2+2cn)；

endfor

endfor

AM为VPU提供向量数据访问时，可同时支持2个向量数据的load/store操作以及标量单元和DMA的向量数据访问，且VPE有4条可并行执行的流水线。为充分利用FT-M7002的以上优势，本文采用循环展开发掘高斯滤波向量算法的指令级并行性。若对上述行滤波部分进行2次循环展开，则1次循环可以处理64个数据，对于输入尺寸较小的图像无法达到预期优化效果。因此，本文进行1次循环展开，1次循环处理32个数据，并对剩余数据设置尾循环处理，充分发挥高斯滤波算法的指令级并行性。

4.3 DMA传输优化

由于AM存储空间有限，当输入矩阵较大时AM一次不能加载整个卷积矩阵，此时输入数据需要存放在核外共享空间DDR中并通过DMA传输到AM，DMA传输的时间会影响整个算法的性能，且列滤波过程中存在数据的不连续访问，导致无法进行向量读写。为了使DMA传输与FT-MT2内核计算并行，从而隐藏DMA传输时间；为了使列滤波计算部分能够连续读取，从而使该部分能够向量化实现，本节主要实现了DMA传输优化。

(1)为提高行滤波计算的速度，用“乒-乓”的方式进行DMA数据传输，可将FT-MT2内核计算与DMA数据传输并行实现。此时将AM空间按地址划分为相等的2部分，分别为Buffer0和Buffer1，先将数据从DDR中通过DMA传输到Buffer0，由于Buffer0中需要保留一部分空间来存放计算结果，因此传输的数据大小应该为Buffer0空间的一半。然后从Buffer0开始计算，Buffer0计算的同时，Buffer1进行数据传输，当Buffer1开始计算时，Buffer0输出上一次的计算结果并启动新数据传输，采用“乒-乓”的数据传输方式可以将计算时间和传输时间重叠起来，提高算法的执行效率。

(2)该算法实现中列滤波过程存在不连续访存，无法通过向量指令进行连续存取，因此需要对行滤波结果进行转置变换，以实现列滤波的连续读取。FT-M7002中的DMA传输模块可以由设计人员自行配置传输方式，比如可以根据设置的帧索引值对相邻2个帧的首数据单元进行地址跳变的读或写，因此可以通过适当配置DMA的索引值，实现矩阵的转置。如使用DMA将DDR中的行滤波结果矩阵O1中的第1行按列存储在AM的O2中，DMA配置中目的帧索引值配置为O2每行首元素的地址差，则DMA会将O1[0][1]根据索引值间隔搬移到O2[1][0]中，O1[0][2]搬移到O2[2][0]中，依此将矩阵O1中第1行转置到矩阵O2中第1列，然后完成剩余行的转置。

5 实验

本节介绍在FT-M7002平台上高斯滤波算法优化实现相对于高斯滤波串行算法的性能提升，以3*3和5*5的高斯核为例，分析不同尺寸输入图像对算法加速比的影响，同时与TMS320C6678中高斯滤波算法性能进行对比，分析2类处理器的单核计算能力。

5.1 实验环境与内容

在飞腾平台的FT-M7002处理器上实现高斯滤波算法优化，调用定时器的计时函数记录该算法执行时间，使用TI平台的高性能数字信号处理器TMS320C6678进行对比分析，具体实验环境如表1所示。

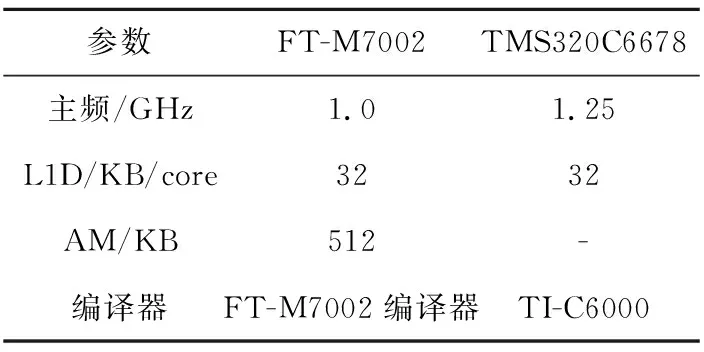
Table 1 Experimental platform parameters表1 实验平台参数

面向飞腾平台的高斯滤波优化算法能够在具体应用中使用的基础是滤波结果的正确性，同时在保证正确性的基础上提高算法执行效率是本文优化的目的。因此，本次实验的内容主要有2部分，分别是正确性验证和性能提升验证。

正确性验证：在FT平台上编写程序，调用前面实现的高斯滤波优化算法，使用FT-M7002编译器编译程序为可执行文件，加载可执行文件到FT-M7002处理器中运行并保存运行结果，与Intel开发的OpenCV图像库中高斯滤波结果进行对比。

性能提升验证：性能提升验证包含2部分，分别是在FT-M7002中相对于串行高斯滤波算法的加速比，以及相对于TI平台的计算性能。

5.2 实验结果与分析

(1)正确性分析。

以3*3和5*5的高斯核为例，在FT平台上运行高斯滤波优化算法并打印结果矩阵，与Intel开发的OpenCV图像库中高斯滤波结果进行对比。将2个结果相减取绝对值，以万分之一为标准，精确度小于万分之一的认为结果正确。结果如表2所示，对于不同尺寸的输入图像，本文算法均能取得正确的处理结果。

Table 2 Results of correctness analysis表2 结果正确性分析

(2)加速比分析。

选取高斯滤波常用3*3和5*5高斯核，分别运行高斯滤波串行算法与高斯滤波优化算法并记录运行时间。在FT-M7002处理器上的测试结果如图5所示，横坐标表示滤波矩阵规模，纵坐标表示本文算法相对于串行高斯滤波算法的加速比。可以看出对于不同大小的输入图像，优化后高斯滤波算法能取得1.3～1.41倍的加速比，由于DMA传输耗时以及算法中生成高斯滤波核、边界填充等模块耗时的影响，该算法性能提升没有达到理论值。

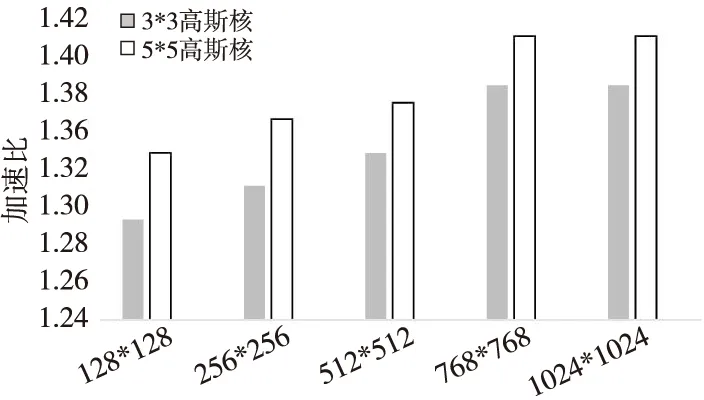
Figure 5 Speedup of optimized Gaussian filtering algorithm图5 优化后高斯滤波算法加速比

从趋势上来看，在滤波核规模一定的情况下，算法加速比随着滤波矩阵规模的增加先增加，后趋于稳定。主要原因在于，本文算法将读入数据都放在DDR存储空间中，由于数据传输耗时导致加速效果达不到理论值，但是随着输入数据的增大，DMA传输耗时所占比重变小，加速效果也有所提升。对于不同高斯核，可以看出，高斯核规模越大加速效果越明显，主要原因是，高斯核越大，每次循环中计算的数据越多，因此优化后的算法能更好地提升循环内数据的并行性。

在TMS320C6678中运行高斯滤波算法并在FT-M7002中运行本文优化算法，分别使用TI与FT平台的计时函数记录运行时间。在FT-M7002中运行本文优化算法时需要先开启Cache选项，测试结果如图6所示，结果表明，对于不同尺寸滤波图像，FT-M7002向量处理器相对于TI多核处理器取得了1.15～1.71倍的加速比。可以看出在滤波核规模一定的情况下，相对于TI平台，FT平台处理不同尺寸图像的性能加速基本相同，但是在图像尺寸一定的情况下，5*5高斯核的FT平台相对于TI平台的性能加速明显高于3*3高斯核的。

相对于TI处理器，FT处理器有更长的向量寄存器，因此单核运算中，针对计算密集型程序FT平台相对于TI平台有一定的计算优势。

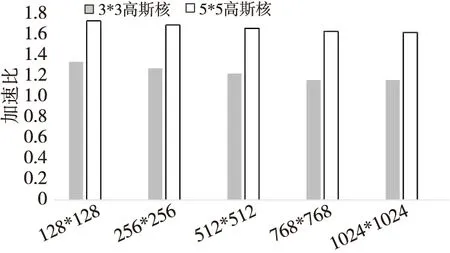
Figure 6 Speedup comparison of optimized Gaussian filtering algorithm with Gaussian filtering algorithm on TI6678图6 优化后高斯滤波算法相对于TI6678中高斯滤波算法加速比

6 结束语

针对国产高性能DSP的快速发展过程中缺乏相应软件应用的问题，本文在深入理解高斯滤波算法的基础上，对高斯滤波算法进行了针对FT-M7002 DSP的体系结构特点的优化实现。为了充分利用该平台的核内资源，本文使用编译器内嵌指令进行手工向量化改写，并使用控制流消除、循环展开等方法挖掘指令级并行性。同时，通过使用“乒-乓”缓存的方式实现了DMA数据传输与向量计算的并行。为了避免计算阶段出现向量访存不连续，在列滤波计算阶段对数组进行转置存放。本文在多种滤波核大小及图像矩阵规模下进行了性能测试，结果表明：相对于没有进行优化的串行实现，优化后阈值分割算法获得了1.3～1.41倍的加速比。同时，相较于dsplib库中高斯滤波算法在TMS320C6678平台上的运行性能，获得了1.15～1.71倍的加速效果，验证了本文优化实现的有效性以及FT DSP核的计算性能优势。然而，该优化实现目前只针对32位输入数据类型，下一步将面向FT DSP核继续完善高斯滤波算法，使其支持更多数据类型。