基于反向学习和种群引导的多目标蝗虫优化算法*

邵鸿南,梁 倩,王李森,马云鹏,项贤鹏

(1.东北财经大学统计学院,辽宁 大连 116000;2.哈尔滨商业大学经济学院，黑龙江 哈尔滨 150000)

1 引言

多目标优化是多准则决策的分支领域，它是涉及多个目标函数同时优化的数学问题。多目标优化不可能使所有的目标都达到最优值，需要在多个相互冲突的目标之间进行权衡，做出最优决策。因此，对于多目标的研究十分重要，应该设计更多的优化算法以解决实际问题。

国内对于蝗虫优化算法GOA(Grasshopper Optimization Algorithm)的研究主要是将算法与其他模型结合并应用在工程问题当中。张伍等[1]采用了二进制版本的蝗虫特征选择法，将蝗虫优化算法与多核模糊粗糙集模型相结合，提出了模糊粗糙集蝗虫优化算法FRSGOA (Fuzzy Rough Set Grasshopper Optimization Algorithm)。陈冬[2]在标准蝗虫优化算法的基础上提出了一种正余弦混沌蝗虫优化算法SCCGOA (Sine Cosine Chaotic Grasshopper Optimization Algorithm)。该算法先由GOA算法搜寻到当前最优位置，之后在该位置进行混沌局部搜索，将正余弦搜索机制引入到混沌变量的波仔映射中。赵然等[3]将Levy随机飞行引入蝗虫优化算法，提高了局部搜索的能力，又加入了线性递减参数的随机突变策略，提出了一种基于 Levy飞行的改进蝗虫优化算法 LBGOA (Grasshopper Optimization Algorithm Based on Levy flight)。

国外对于蝗虫优化算法的研究开始得比较早。Mirjalili等[4]提出了多目标蝗虫优化算法MOGOA(Multi-Objective Grasshopper Optimization Algorithm)，用外部档案来保存帕累托最优解，然后利用轮盘赌选择引导者，在多种测试函数上都表现优异。Talaat等[5]结合多层前馈神经网络和蝗虫优化算法，使用组合模型进行高精度的负荷预测，实验结果表明GOA的引入能够大幅度提升模型的准确性。Gampa等[6]提出了一种基于两阶段蝗虫优化算法的模糊多目标方法，利用该方法可以优化分布式发电和并联电容器的大小和分配，确定电动汽车充电站的最佳位置和充电站的车辆数量。由以上文献可以看出，目前关于多目标蝗虫优化算法的研究比较少，应用也不够广泛，学者们都致力于算法的应用，而忽略了算法本身的改进。蝗虫优化算法位置的更新公式仍具有潜在价值，平衡开发与探索之间协作还有很大的改进空间。蝗虫优化算法在各方面都展现出了巨大的研究价值，因此对于多目标蝗虫优化算法的研究仍需要投入大量时间。

与之前学者的研究成果相比较，本文所提出的基于反向学习和种群引导的多目标蝗虫优化算法OPMOGOA(Multi-Objective Grasshopper Optimization Algorithm based on Opposition-based learning and Population guidance)的创新点有以下几点：

(1)种群引导机制的使用。单一的最优解引导机制在算法的后期不能全面引导种群向着更好的分布进化，而种群引导机制[7]的使用能够较好地利用一部分最优解所包含的信息引导种群的演化，这对于多目标优化算法所求解的分布性有着巨大的提升作用。

(2)反向学习机制[8]的使用。反向学习机制的应用能够使种群搜索的范围更加广泛，种群初始化时使用反向学习机制会使得初始种群分布更加合理。

(3)高斯突变[9]的使用。高斯突变较高概率下会围绕中心周围进行突变，这就使得迭代后期能够更加细致地搜索最优解的附近。

2 基本知识

2.1 多目标优化问题

一个具有N个维度的决策变量和M个维度的目标函数的问题可以描述为式(1)所示:

minY=[f1(Xi),f2(Xi),…,fM(Xi)]

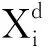
(1)

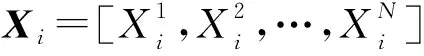
决策变量解A优于解B，则A在所有的目标函数都小于或等于B，并且至少在一个目标函数中，A是严格优于B的，记为AB。在解集合中，不存在任何一个解严格优于当前解，这样的解称为最优解。由帕累托最优解构成的集合被称为帕累托最优解集。所有的帕累托最优解集所对应的目标向量就是帕累托前沿。

2.2 蝗虫优化算法

蝗虫优化算法[10]的核心思想是蝗虫根据食物的位置和蝗虫群其他个体的位置进行跳跃移动，蝗虫之间有排斥区、舒适区和吸引区，蝗虫根据数学模型所提供的位置更新公式更新所在位置。所有的蝗虫进行移动后，更新所有蝗虫的适应度值，食物的位置由最优的适应度值确定，当所有的蝗虫都移动到舒适区，蝗虫将不再移动。

蝗虫种群中各个蝗虫的位置更新模型表示为Xi=Si+Gi+Ai,其中Xi代表第i个蝗虫的位置，即决策变量，Si代表社会影响因素，Gi代表重力影响因素，Ai代表风向影响因素。Si的定义如式(2)所示：

(2)

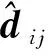
(3)

其中，f代表吸引力强度，通常设置为0.5，l代表吸引力长度比例参数，通常设置为1.5。r代表2个个体间的距离，当S(r)>0时,2只蝗虫处于吸引状态；当S(r)=0时,2只蝗虫处于舒适状态；当S(r)<0时，2只蝗虫处于排斥状态。

Gi的计算公式如式(4)所示：

(4)

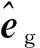
Ai的计算公式如式(5)所示：

(5)

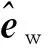
将上述公式整合后得到：

(6)

但是这一模型并不能直接应用于求解问题，因此对它进行如下改进：

(7)

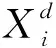
3 反向学习和种群引导的多目标蝗虫优化算法

3.1 反向学习机制

为了更好地学习反向学习机制，首先来解释反向点的概念，以一维标量为例，图1所示a的反向点为z。

Figure 1 Reverse point图1 反向点

a的上下限分别是lower和upper，则lower+upper-a称为a的反向点。明确反向点的定义之后，在每次位置更新后，求出每个解的反向点，比较当前解和反向点的目标函数值，如果反向点有更优的目标值，则用反向点代替当前解，否则保持不变。本文将反向学习机制应用于种群初始化策略和迭代更新过程。

3.2 高斯变异

为了解决多目标算法陷入局部最优解的问题，本文在位置更新时加入了高斯变异算子。高斯变异算子相比于其他的变异算子，在均值附近变异的概率最大，而产生变异是以上代位置为中心的变异，这就使得算法在局部的开发更加有效。在算法运行过程中，每个个体决策变量的每个维度都有一定几率发生标准差为σ的高斯变异，其数学模型如式(8)～式(10)所示：

(8)

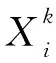
(9)

σ=(ubk-lbk)/6

(10)

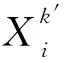
3.3 种群引导

由于蝗虫优化算法需要最优解作为引导，引导其他的蝗虫向最优解移动，因此，最优解的选取至关重要。但是，由于偶然性的存在，有时选择的最优解不够合理。并且全局最优解不应该只局限于一个固定的解，应该是较为优秀的解的集合。本文所提到的种群引导正是基于这样的目的，每次从帕累托等级为1的个体中随机选取10%作为最优解的集合，每个蝗虫个体从最优的10%的解中随机选取一个向其移动，经过这种引导方式的解有更好的分布。

3.4 帕累托等级排序

通过非支配排序将种群数为n的种群分类为分级的帕累托前沿。首先将种群中所有的帕累托前沿求出，标记帕累托前沿等级为1。之后将帕累托等级为1的个体忽略，在剩下的个体中求帕累托前沿，并记录帕累托等级为2，之后循环进行，直至将所有的解都分类。通过引入帕累托等级[11]和拥挤度的计算，能够将所有的解进行排序，以便在种群混合时能够选择出比较好的前N个解。

3.5 拥挤距离

拥挤距离用来描述非支配解分布的特征，以便选出帕累托最优集中10%的优质解。在帕累托解集中，每个非支配解都有一个拥挤距离，用于表示离它最近的非支配解在各个目标函数维度上的距离之和。拥挤距离值越大，说明离当前解最近的解位置较远，即帕累托解比较稀疏。相反，拥挤距离越小，说明离当前解最近的解位置较近，即帕累托解越密集。引入拥挤距离的目的是通过当前帕累托最优解的分布情况来选择最优帕累托解，以引导种群发现使得帕累托前沿更均匀的解。而在帕累托前沿中的边界解中，拥挤距离被设定为inf，其他解的拥挤距离的计算公式如式(11)所示:

(11)

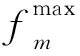
3.6 算法流程

本文算法首先通过反向学习机制来初始化种群，利用最优解的10%作为引导者进行位置更新，更新位置后结合反向学习机制，选择较优解作为子代，并以一定的概率产生高斯突变，将最终产生的子代与父代混合，根据精英保留策略筛选出较优解进入下一代。该过程不断迭代直至达到最大迭代次数。具体流程如算法1所示。

算法1OPMOGOA

输入:种群数量，最大迭代次数。

输出:帕累托最优解。

步骤1初始化种群并计算反向点及其适应度值。

步骤2将种群合并后计算帕累托等级和拥挤距离。优先选择较低的帕累托等级，当帕累托等级相同时选择拥挤距离较大的解。根据此规则选取前N个个体作为初始种群。

步骤3从帕累托等级为1的个体中随机选择10%作为种群引导。

步骤4每个个体从已选取的10%的解中随机选取一个作为引导者，对所有的蝗虫位置进行更新。

步骤5计算反向点与当前候选解，选择更优解进入下一代，如果反向点与当前候选解互不支配，以0.5的概率进行选择。

步骤6对种群中每个蝗虫产生一个随机数，当随机数小于p时对该蝗虫位置进行高斯突变。

步骤7将子代与父代进行合并，重新计算帕累托等级和拥挤距离，根据步骤2的筛选规则选择前N个个体进入下一代，以保证种群数量维持不变。

步骤8判断是否满足最大迭代次数，不满足最大迭代次数则重新执行步骤3～步骤8。

4 实验

4.1 实验设置

为了进一步验证改进的算法具有良好的表现，本文选取了4种算法与改进的算法进行比较，分别是多目标粒子群优化MOPSO(Multiple Objective Particle Swarm Optimization)算法[12]、多目标布谷鸟搜索MOCS(Multi-Objective Cuckoo Search)算法[13]、经典多目标蝗虫优化算法MOGOA(Multi-Objective Grasshopper Optimization Algorithm)[14]和多目标鲸鱼优化算法MOWOA(Multi-Objective Whale Optimization Algorithm)[15],测试函数选择2个目标的测试函数ZDT1和ZDT2[16]，以及3个目标函数的VNT2和VNT3[17]。在测试函数中分为有约束条件和没有约束条件，这就给帕累托前沿的求解带来了巨大的困难，但是OPMOGOA的表现依旧出色。实验环境为64位Windows 10系统，CPU为AMD R5 3500U 2.10 GHz，内存为8 GB，编程语言为Matlab。每个算法独立运行30次然后计算出反转世代距离IGD(Inverted Generational Distance)[18]和超体积指标HV(Hyper Volume)[19]的均值与方差。

4.2 性能指标

4.2.1 反转世代距离

反转世代距离IGD是每个真实帕累托前沿上的参考点与算法所求解的最近距离的平均值，如式(12)所示：

(12)

其中，P为分布在真实帕累托前沿上的点的集合，|P|为集合P中的点的个数，Q为算法获取的帕累托最优解的集合，v代表测试函数中真实帕累托前沿上的参考点集合。d(v,Q)代表v与集合Q中的点的最小欧氏距离。当算法获得的解比较集中时，d(v,Q)的值较大，导致IGD值较大。当获得的解离帕累托真实前沿比较远时，参考点与获得的解之间的距离之和则会相对较大。因此，IGD能够同时评价多样性和收敛性。IGD值越小，说明算法所求的解离真实帕累托前沿越近或者解的分布越均匀。

4.2.2 超体积指标

超体积指标HV是度量非支配解集所支配区域的大小。

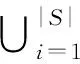
(13)

其中，δ表示 Lebesgue 测度，用来测量体积。 |S|表示非支配解集中解的数目，vi表示参照点与解集中第i个解构成的超体积。HV值越大，表示算法的综合性能越好。

4.3 实验结果与分析

4.3.1 种群引导、高斯变异、反向学习机制的验证

为了进一步体现算法中引入种群引导、高斯变异算子和反向学习机制的作用，本文将所提出的算法在ZDT1函数上进行了实验，采用控制变量法，在种群数量和迭代次数相同的情况下对比了引入改进和未引入改进时的实验指标。鉴于各部分改进对于算法收敛速度的提升效果的影响各不相同，因此各对比实验的迭代次数分别设置为60次、80次和90次。实验分别运行30次，同样取均值作为比较，记引入种群引导的算法为PG-MOGOA，引入高斯变异的算法为GS-MOGOA，引入反向学习的算法为OBL-MOGOA，未引入相应改进的算法记为MOGOA。各实验结果对比图如图2～图4所示，其中横坐标和纵坐标分别表示测试函数ZDT1的目标函数维度。

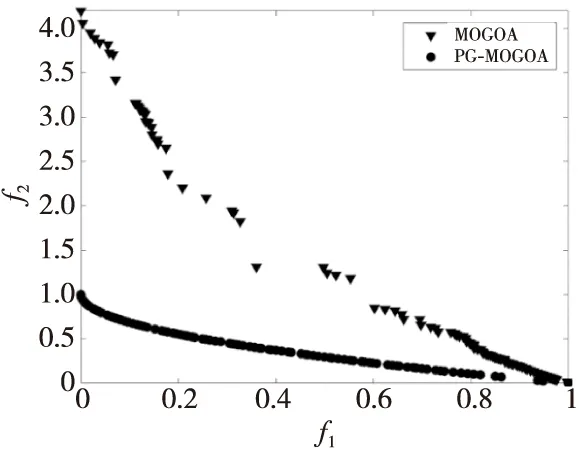
Figure 2 Comparison of population guidance图2 种群引导的对比图

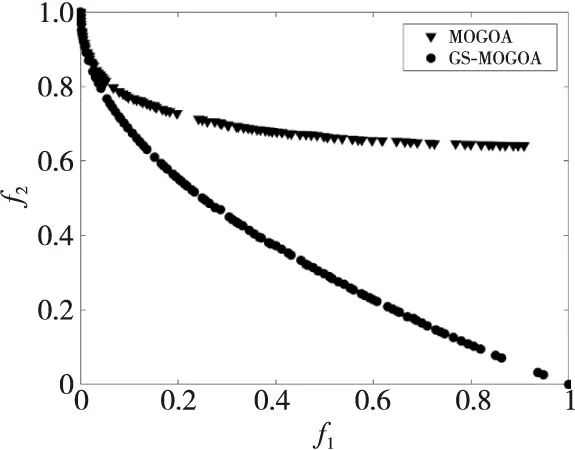
Figure 3 Comparison of Gaussian mutation图3 高斯变异的对比图

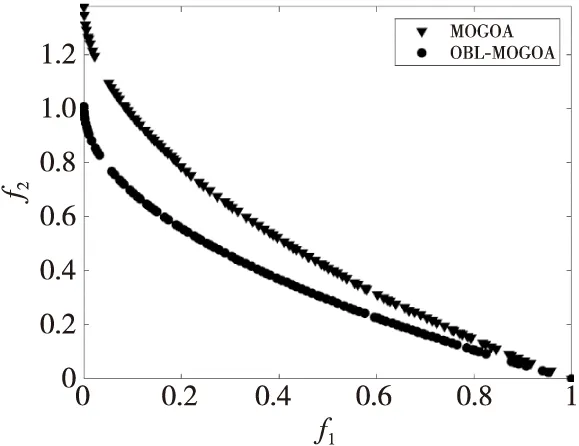
Figure 4 Comparison of back learning mechanism图4 反向学习机制的对比图

未引入种群引导的MOGOA 30次实验的IGD和HV均值分别是3.192E-01，3.081E-01，PG-MOGOA的IGD和HV均值分别是1.361E-02，7.054E-01，可见种群引导对算法的提升效果十分明显。结合图2可以看出，未引入种群引导时，算法所求的帕累托最优解集中在右下角，并且解的分布并不均匀。这是由于算法在选择最优解时不能全面地引导种群的进化，若算法每次仅选择单个最优解进行引导会让解的分布比较集中。因此，种群引导的引入能够让解的分布性得到明显的提升。

未引入高斯变异的MOGOA的IGD和HV均值分别是3.447E-02，6.844E-01，引入后的均值分别是1.4121E-02，7.0476E-01，高斯变异的引入使得各指标值都有了改善。结合图3可以看出，未引入高斯变异时的解均匀且光滑，已经陷入局部最优，而高斯变异的引入能使算法跳出局部最优解，从而使收敛性得到提升。

未引入反向学习机制的MOGOA的IGD和HV均值分别是1.400E-02，7.049E-01，引入后的均值分别是8.5442E-03,7.129E-01。从图4中可以看出，反向学习机制的引入对算法有着相对较小的提升作用。在算法中，反向学习机制不仅应用在种群初始化中，也应用在种群的位置更新过程中。初始化时反向学习机制的引入使得算法的初始分布更加全面，迭代更新过程中的应用使算法的搜索范围更为广泛，使算法的性能有了良好的改善。

4.3.2 与其他算法的比较

从表1来看，OPMOGOA在ZDT1，ZDT2上的IGD值分别为1.367E-02，5.775E-03，相比于另外4种算法本文所提算法均值最小,且方差也最小，分别为8.760E-03，1.360E-03，可以看出OPMOGOA求得的解在收敛性和均匀性上的表现都十分出色。由于ZDT2函数的特殊性，MOCS、MOPSO、MOWOA和MOGOA都出现过收敛于一点，该点在帕累托最优前沿上，这会导致IGD值为0，使总体均值偏小，因此在这里将所有IGD为0的实验结果去掉后求平均。在ZDT2上运行的30次中，MOWOA、MOGOA、MOPSO、OPMOGOA和MOCS分别有11次、3次、11次、1次和0次IGD值为0的情况。可见OPMOGOA跳出局部最优的能力较强。虽然MOCS没有出现一次这种情况，但是其IGD值为3.377E-01，相对表现比较差。从表2来看，OPMOGOA在ZDT1和ZDT2上的HV值最大，分别为7.056E-01，4.426E-01，并且方差均为最小，表现十分稳定，在2个目标的ZDT系列函数上，MOGOA能够较好地收敛到帕累托前沿。

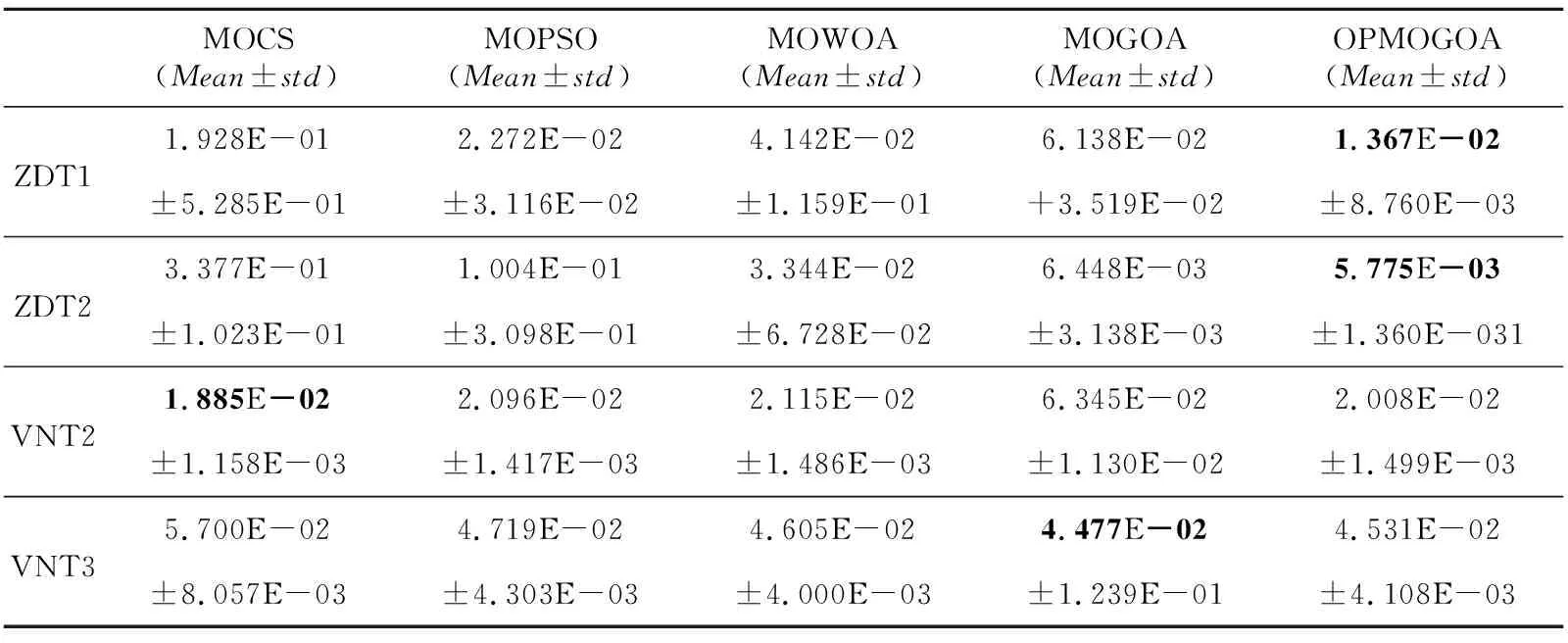
Table 1 Comparsion of IGD value of algorithms表1 各算法的IGD值比较

表1和表2中所示分别为各算法的IGD和HV均值mean和方差std。从表1来看，在VNT2上OPMOGOA的IGD值仅次于MOCS的IGD值，MOGOA的表现最差。在VNT3上MOGOA的IGD值最小，为4.477E-02，改进后的OPMOGOA反而略差，但是比另3种算法更好。从表2来看，在VNT2上，OPMOGOA的HV值为2.041E-00，位于第1位，相比经典的MOGOA算法性能有所提升。在VNT3上，OPMOGOA的HV值仍然最大，为1.840E-01。除MOGOA的性能较差之外，其他3种算法之间相差不大。总的来说，5种算法在3个目标的VNT系列上的表现相差不大，但MOGOA的算法有着一定的优势。

5 结束语

随着信息化技术越来越发达，产生的信息越来越多样化，多目标算法优化对象的规模越来越大，约束条件也越来越多，因此学者们对于多目标算法性能的要求也越来越高，这给多目标优化带来了更大的挑战 。本文所提出的多目标蝗虫优化算法将反向学习机制应用到产生初始解和迭代进化的过程中，在蝗虫移动过程中增加高斯变异算子，并加入帕累托最优集中的随机解集引导种群的移动，最后根据帕累托等级和拥挤度距离筛选精英个体进行保留。实验结果表明，3种改进机制的引入在一定程度上提升了算法的性能。此外，本文的OPMOGOA算法相对于其他4种算法在IGD和HV上都有着明显的优势，表明了多目标蝗虫优化算法有着较大的研究价值。未来的研究工作将从以下2个方面进行：(1)研究OPMOGOA的应用领域，应用多目标蝗虫优化算法解决更多的实际问题；(2)改进多目标蝗虫优化算法，使其适应更难更复杂的多目标问题。

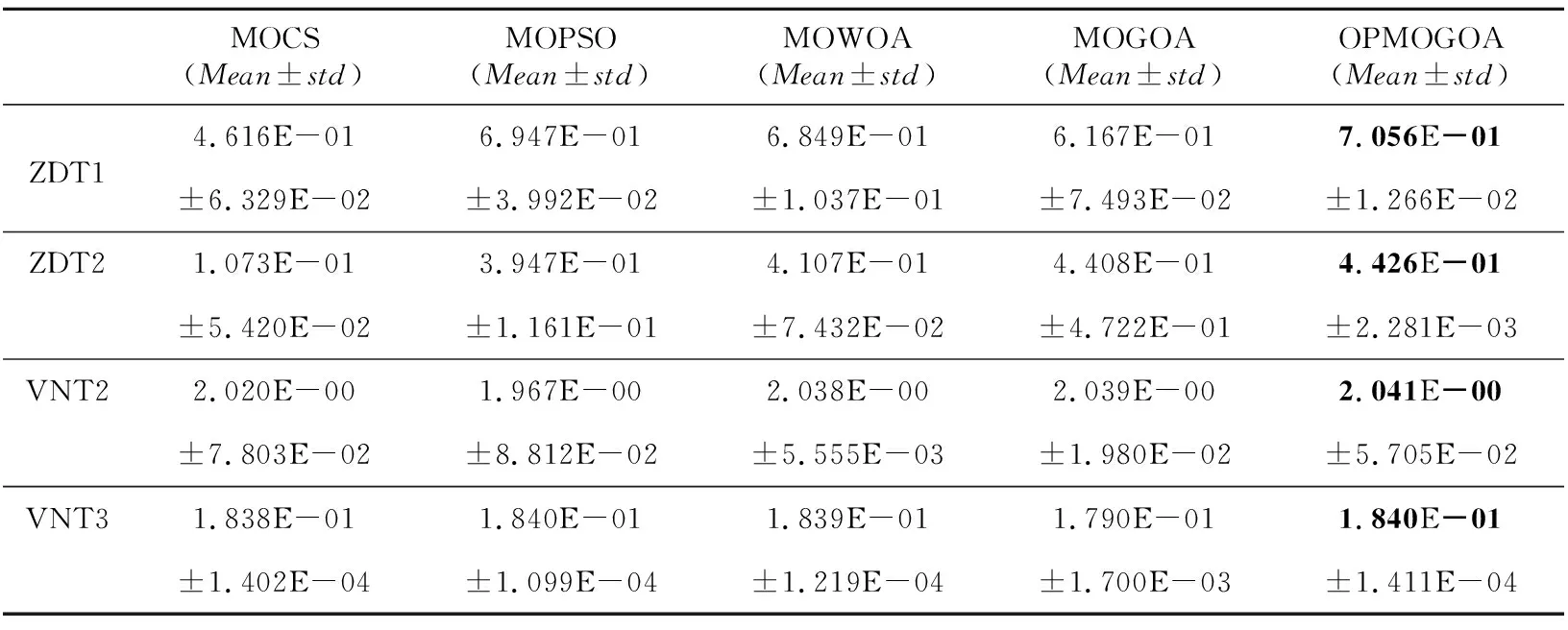
Table 2 Comparsion of HV value of algorithms表2 各算法HV值比较