弹架间隙对导弹发射扰动的影响特性研究*

何泽鹏 张雁 赵良玉 傅德彬 李云峰

（1.北京理工大学宇航学院，北京100081）（2.中国空间技术研究院钱学森空间技术实验室，北京100094）（3.吉林江机特种工业有限公司技术部，吉林132021）

引言

长期以来，火箭导弹发射扰动问题受到广泛关注.尤其针对如今的导弹发射系统，根据实际装配需要，在设计弹体与发射箱/架的装配时，总会保留一定的配合间隙，该间隙会导致弹体在发射过程中产生恶性扰动，给发射安全性带来隐患，严重影响弹体离轨和出筒后的自动控制.因此，弹架间隙对发射扰动影响的探究分析成为亟需的研究课题.

早期，文献［1］建立了带有间隙的弹性机构数学模型，并推导了运动动力学方程，以此来确定机械在有间隙情况下的动力学响应.文献［2］基于运动学分析提出了三类间隙影响的理论分析方法，而后与多体动力学软件ADAMS的仿真结果进行对比与分析，结果可满足实际工程间隙超差影响分析的需求.文献［3］采用混合方法，建立了沿柔性发射装置推进的旋转火箭的耦合动力学方程，以获得系统的瞬态动力学响应 .骆连珍等［4，5］通过建立炮弹的多体动力学运动模型，研究发射装置的振动和炮弹间隙对火箭弹产生的初始扰动影响.文献［6］通过建立一种含摩擦碰撞的模型，探究了间隙绞对机动武器的发射系统的影响.文献［7］开发服从正态分布的随机间隙模型子程序，基于动力学仿真模型，计算随机性间隙对导弹发射系统的影响.文献［8］通过建立舰载导弹垂发系统的动力学仿真模型，研究了装配间隙参数对系统的影响.文献［9］采用物理模型和软件分析方法研究发射装置液压缸振动、发射仰角和弹架配合间隙等因素对火箭发射扰动的影响.文献［10］采用有限元法分析了相关参数对弹丸起始扰动的影响规律，并对火炮结构参数的影响程度进行灵敏度分析.

本文针对含发射架的导弹在发射过程中，弹架间隙对其发射扰动的影响问题，提出了随机扰动激励与多体动力学相结合的计算方法.该方法以多体系统动力学为基础，建立能够模拟导弹与发射架相互作用的发射动力学模型，并将赫兹碰撞接触算法、随机过载的模型与多体动力学模型相耦合，从而计算获得初始扰动响应的参数.并以某导弹为实例，建立其耦合模型，对计算结果进行了详细分析.该方法可为以后相关的弹架间隙扰动问题，提出新的参考依据.

1 发射动力学模型分析

1.1 多刚体动力学模型

对于含N个刚体作空间运动的多刚体系统，取定一个惯性参考基e和每个刚体的连体基ei，质心相对于惯性基的坐标(xi，yi，zi)与连体基相对于惯性基的欧拉四元数(λ0i，λ1i，λ2i，λ3i)构成描述刚体βi的笛卡尔坐标阵［11-15］为：

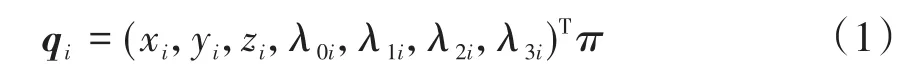
则对于该含N个刚体组成的系统，每个刚体用上述式（1）描述位形，描述整个多体系统位形的坐标总数为7N个.引入拉格朗日乘子，推导得到整个系统的动力学方程可得

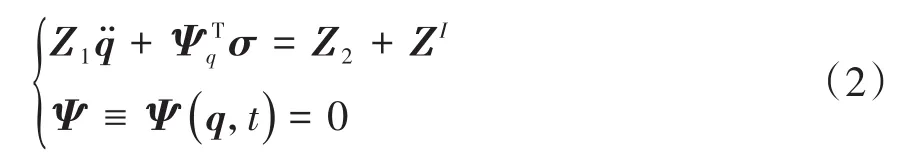
其中，Z1为广义质量阵，Z2为力阵，ZI为惯性力阵，σ=(σ1…σs)T为约束方程对应的拉格朗日乘子阵.

1.2 赫兹碰撞模型

发射过程中，发射装置与弹体之间、发射装置与平台或地面之间，除传统约束外，往往还包含大量的接触关系，而这些接触关系和状态，又是引起发射扰动的主要因素之一.在研究模型中，利用运动副模拟物体间的相互约束关系，利用基于碰撞函数的接触算法［16-18］模拟接触关系，如图1所示.

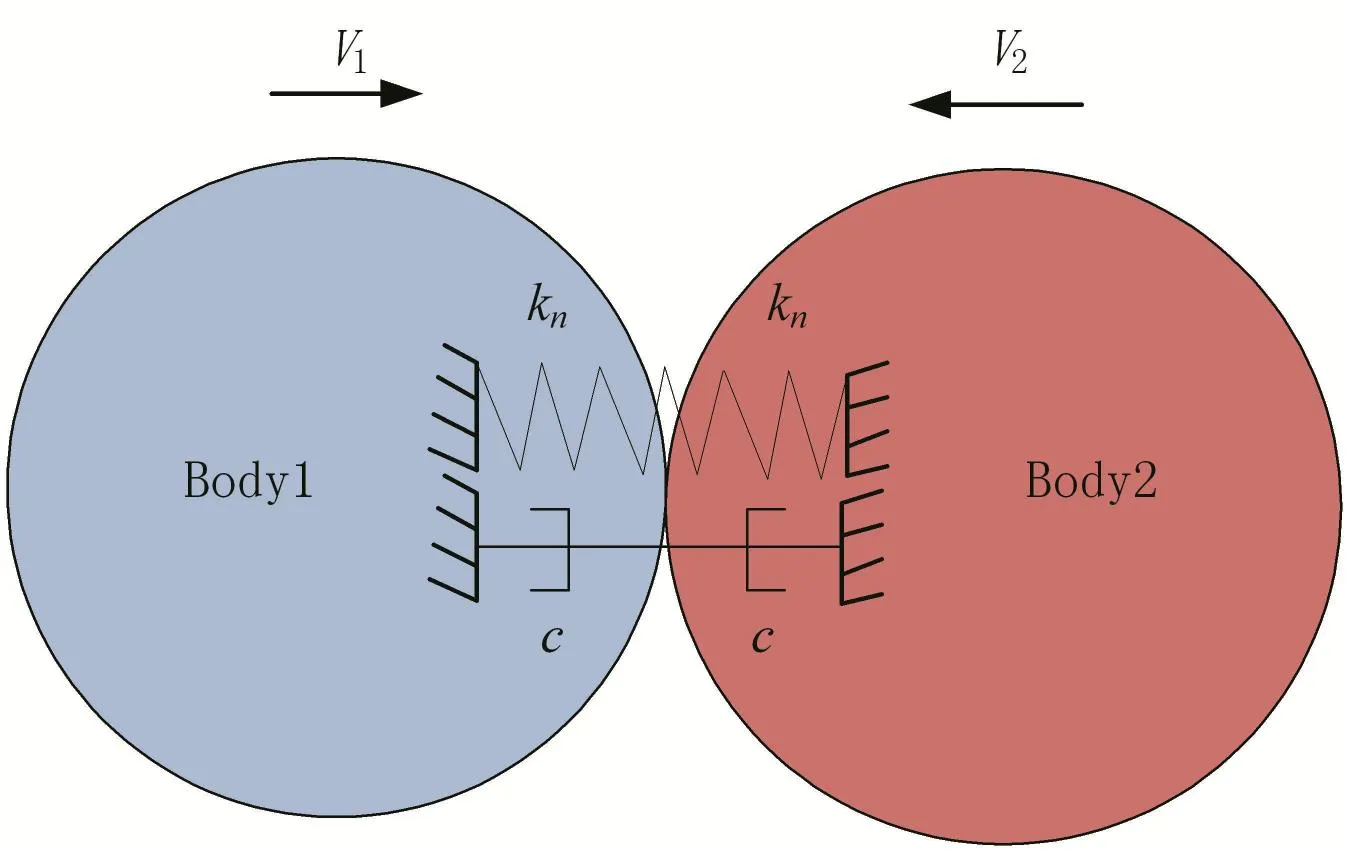
图1 碰撞接触模型Fig.1 Collision contact model

上述碰撞模型的接触力计算公式可表示为：

其中，Fn为法向接触力，kn为刚体的刚度，δ为碰撞物体变形量，e为物体的渗透指数，c为阻尼系数为两个物体的相对速度.

1.3 随机过载模型

为满足装配要求，弹架配合通常留有一定的间隙，如图2所示.在发射过程中，弹架配合间隙同样是引起初始扰动的重要因素.由于在实际火箭弹在发射过程中，在不可确定因素的影响下，火箭弹的支脚与发射架之间的作用力也不尽相同，为模拟发射约束段定向导轨与弹上滑块间的配合间隙作用，并更好地模拟火箭弹在发射过程中的真实情况，因此引入随机过载模型［19-21］，在多体动力学模型中将受间隙尺寸影响的随机扰动力作用在弹体上，并通过接触状态模拟随机扰动作用下的弹架动态响应.

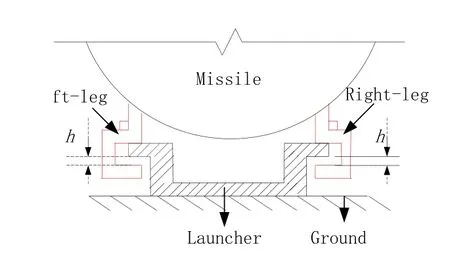
图2 导轨与定向件的配合间隙Fig.2 The fit clearance between the guide rail and the directional part

作用于弹体的随机过载表示为：

其中，A(h)为与间隙尺寸有关的过载幅值，R(t)为取值范围在0和1之间的随机数.

过载幅值采用下式计算：

其中，h为弹体支脚与发射架之间的配合间隙，λ为导轨平度的波长，v1为弹体速度，g为重力加速度.

1.4 气动力与气动力矩模型

依据参考文献［22］和参考文献［23］，本文中的气动力与气动力矩模型采用转换后弹体坐标Ox1y1z1下的气动力与气动力矩，具体如下.

在弹体坐标系下的气动力为：

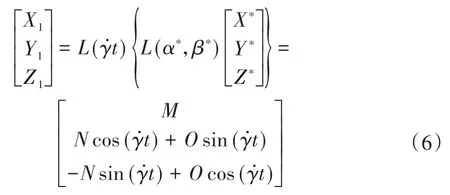
其中，X∗、Y∗和Z∗分别为准速度坐标系下的阻力、升力和侧向力，α∗为准攻角，β∗为准侧滑角̇为滚

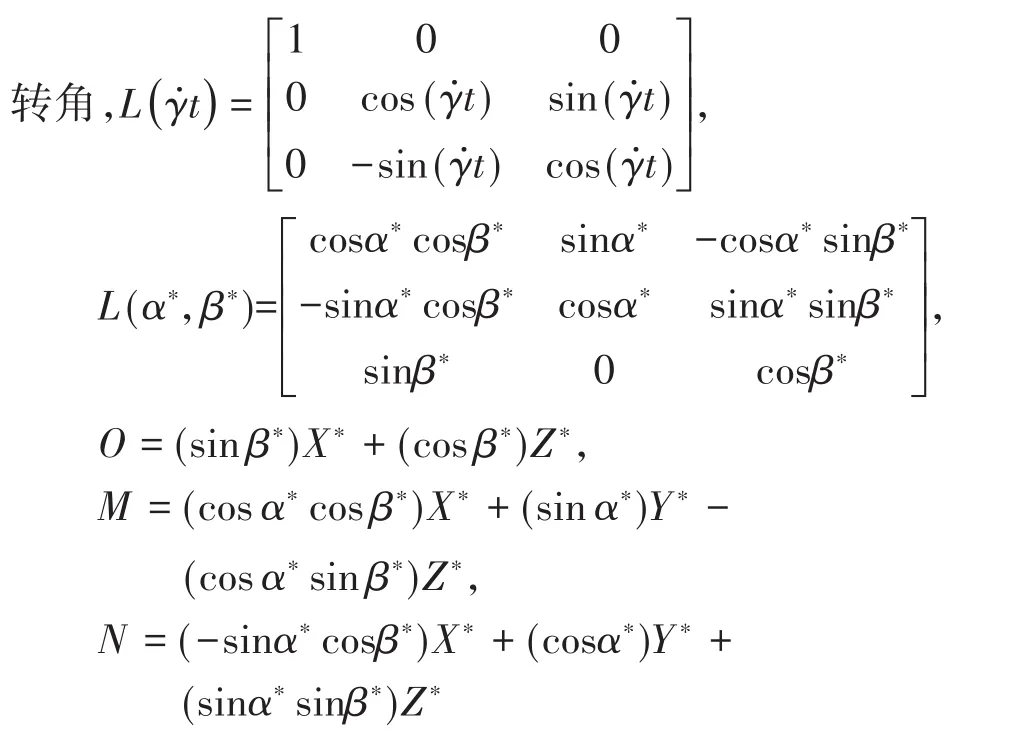
在弹体坐标系下，弹体承受的力矩可由准弹体坐标系下的力矩的关系式获得：

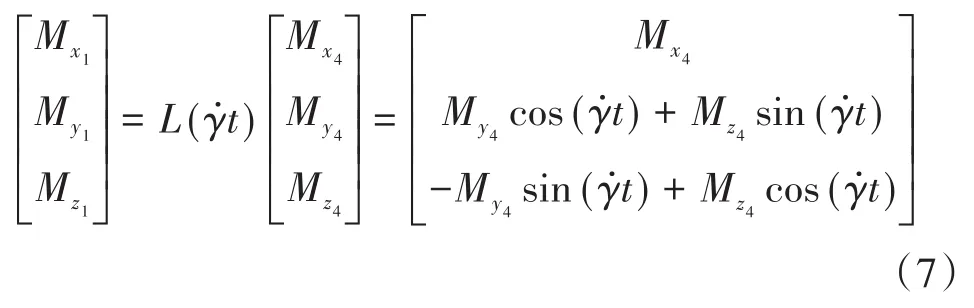
在分析计算过程中，主要利用多体动力学软件Adams进行求解.而多刚体动力学模型是Adams的理论模型，将赫兹碰撞模型、随机过载模型和气动力与气动力矩模型以公式计算的方式引入其中，建立其耦合动力学模型并进行求解计算.

2 基于含发射架的导弹实例分析

2.1 实例模型及参数

基于上述的基础理论，利用多体动力学软件ADAMS，对含发射架的导弹发射系统进行如下耦合模型的建立.其多体动力学简化模型包括：地面、发射架导轨、弹体支脚和弹体四部分，各部件间的约束关系如图3.其中，图中的坐标系OXYZ为地面坐标系.

图3 导弹发射系统的多体动力学简化模型Fig.3 The simplified multibody dynamic model of a missile launching system

在计算模型中，以地面坐标系为全局坐标系，并在弹体质心位置建立多个局部坐标系，弹体上的局部坐标系方向与弹体坐标系相同.所有坐标系均为右手坐标系.该弹体的质量为11.7kg，弹体的赤道转动惯量为 0.032kg·m2，极转动惯量为0.318kg·m2，弹长1m，质心位于距弹头640mm的轴线上，发射轨的有效长度为200mm，发射角度为6°，发射前已将弹体放置在导轨上，并采用同时离轨方案，且弹体在离轨飞行中适当考虑了气动载荷作用的影响.

其中的同时离轨［23］方案如下图4所示，图中Rear-leg表示火箭弹的后支脚，Front-leg表示火箭弹的前支脚，Launcher表示发射架，图4中的（a）为火箭弹在发射轨道上，此时前后支脚在轨，图4中的（b）为火箭弹在离开发射轨道，此时前后支脚离轨.由于发射轨道的前后端上下距离不同，前端距离短，后端距离长，而火箭弹的前后支脚的距离也是前端距离短，后端距离长，以保证火箭弹在离轨时前后支脚同时离开发射轨道.

图4 同时离轨示意图Fig.4 An illustration of simultaneous derailment

计算用到的接触参数设置与参考文献［7］相同，发生过程与文献［22］中相同，并且只考虑发射约束段和无控飞行段，约束段指弹体在轨阶段，无控飞行段为弹体离轨后至飞行0.6s时间内.

2.2 弹道计算典型响应

设置模型中的弹架间隙为1mm，通过对上述导弹发射耦合模型的求解计算，获得了以下典型的动力学响应，具体分析如下.

（1）弹架间接触力分析

图4表示发射过程中导弹支脚与导轨间的接触作用力，其中包含左后、左前、右后、右前支脚与到导轨间的接触力.从图中可以看出，由于本文中的导弹发射模型采用同时离轨方案，四个支脚接触力持续时间均为0.0414s左右，表明前后支脚同时离开了定向导轨.又因为弹体受支脚与导轨间的间隙和碰撞作用，弹体支脚与导轨间的作用力呈振荡变化趋势，并且四个支脚受到的最大作用力为710N.

（2）弹体飞行姿态分析

图5给出发射2s内弹体俯仰角、弹道倾角和准攻角变化曲线.点火初期，由于弹体轴向速度很低，支脚与导轨接触力引起的Y向速度相对较大，弹体姿态角出现瞬时震荡，但对后续计算结果影响很小；随着弹体轴向速度增加，初始俯仰角和弹道倾角稳定在5°到7.5°之间，初始攻角为零；弹体离轨后，俯仰角先逐渐增加，在受重力产生的弹体下沉速度影响下，弹体弹道倾角逐渐减小，准攻角快速增加至1.9°左右；此后由于弹体受到气动载荷的作用，弹体俯仰角和准攻角先逐渐减小后增加，在一定范围内成波动变化，弹道倾角也先增加后减小，在一定范围内成波动变化.

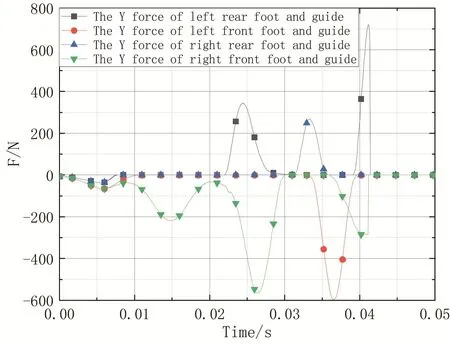
图5 弹体支脚与导轨间的接触力曲线Fig.5 The contact force curve between the projectile and the guide rail

整个考察时间范围内，准攻角与弹道倾角之和等于俯仰角，与理论状态一致，且符合实验数据，表明模型响应是合理的.

3 不同间隙作用对弹体飞行的影响

3.1 不同间隙对弹体飞行姿态的影响

为探究弹架间隙对火箭、导弹发射过程中的扰动响应作用，在上述多体动力学模型基础上，分别设置弹架间隙为 0.2mm、0.4mm、0.6mm、0.8mm、1.0mm和1.2mm，求解获得不同弹架间隙对弹体飞行姿态作用的影响.根据实际情况，弹体在0.041s时刻离轨，在0.6s时刻开始起控，因此在后续分析中，注重分析0.6s前弹体在无控飞行段的飞行姿态.

（1）不同间隙对弹体飞行俯仰角的影响

图6表示在不同弹架间隙作用下弹体的俯仰角变化曲线图.由图可知：弹体在离轨前，受到扰动力影响作用，使得弹体的俯仰角在初始离轨段有着较大的波动变化；当弹体在离轨后，弹体在推力偏心和外激励作用的影响下，俯仰角呈现先增加后减小的波动变化趋势；随着弹架间隙增加，导轨与弹体支脚间产生的扰动力越大，弹体的俯仰角会随着弹架间隙的增加而减小，当弹架间隙从0.2mm变化到1.2mm时，俯仰角在0.48s时的最大差值为3.93°.

图6 俯仰角、弹道倾角及准攻角的变化曲线Fig.6 The variation curve of pitch angle，flight path angle and quasi attack angle

（2）不同间隙对弹体飞行攻角的影响

图7是在不同弹架间隙作用下弹体的攻角变化曲线图.由图可知：随着弹架间隙的增加，弹体在离轨前受到的扰动力较大，使得弹体的攻角在初始段出现较大的波动变化；弹体离轨后，在推力和自身外激励的影响作用下，弹体的攻角呈先增加的趋势，后由于推力撤去，攻角逐渐减小；弹体在离轨后，由于间隙扰动力影响的后续效应存在，弹架间隙越大，攻角反而越小，在0.6s时刻，攻角的最大差值为1.89°.

图7 不同间隙下弹体俯仰角变化曲线Fig.7 The variation curve of pitch angle of projectile body with different clearance

（3）不同间隙对弹体飞行弹道倾角的影响

图8是在不同弹架间隙作用下弹体的弹道倾角变化曲线图.由图可知：随着弹架间隙的增加，弹体在离轨前受到的扰动力较大，使得弹体的弹道倾角在初始段出现较大的波动变化；弹体离轨后，在推力和外激励的影响作用下，弹体的弹道倾角呈先增加后平稳的变化趋势；随着弹架间隙增加，弹道倾角反而越小，且弹架间隙在1.0mm以上，弹道倾角基本不变，在0.6s时刻，弹道倾角的最大差值为2.38°.

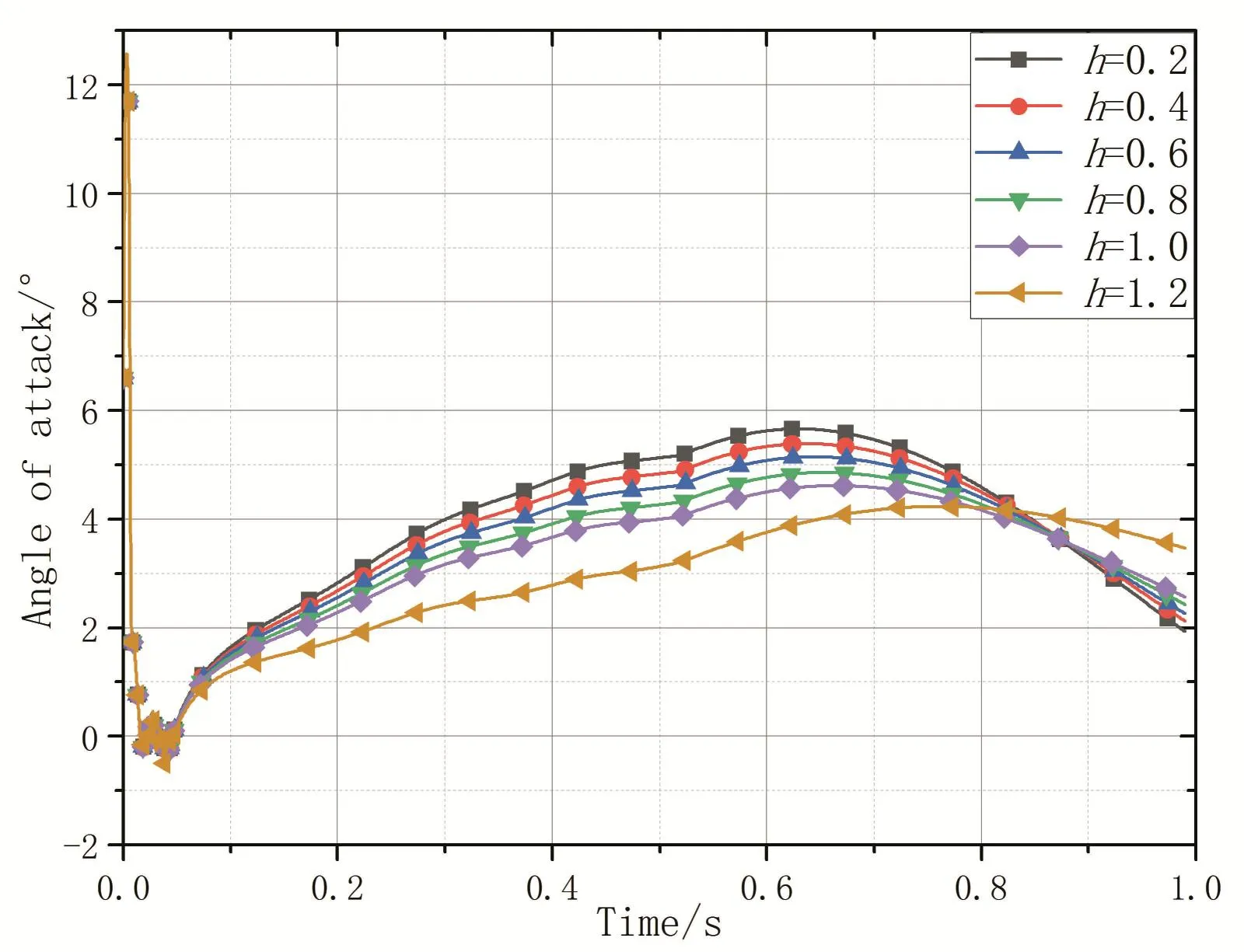
图8 不同间隙下弹体攻角变化曲线Fig.8 The variation curve of attack angle of projectile body with different clearance

由此可知：弹架间隙的大小对弹体的飞行姿态有着较大的影响作用，弹架间隙越大，会使得弹体的飞行俯仰角和攻角减小，飞行轨迹减低，易出现弹体掉落的现象.

3.2 弹道计算典型响应

由于弹体在0.6s时刻开始受到控制，因此这里注重分析弹体在此时刻的飞行姿态及飞行位置.

（1）不同间隙下弹体在0.6s时刻的飞行姿态

图9表示的是在不同间隙下，弹体在0.6s时刻时的飞行姿态.其中，Pitch表示弹体的俯仰角；Alpha攻角表示弹体的攻角；Bata表示弹体的侧滑角，横坐标H表示弹架间隙的大小.从图中可知，随着弹架间隙的增加，弹体在0.6s时刻的俯仰角、攻角和侧滑角都呈下降的趋势，并且由于弹架间隙越大，会使得弹体的飞行俯仰角和攻角减小，飞行轨迹减低，易出现弹体掉落的现象.

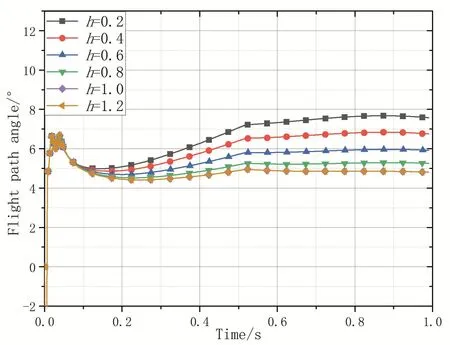
图9 不同间隙下弹体弹道倾角变化曲线Fig.9 The variation curve of flight path angle of the projectile body with different clearances

（2）不同间隙下弹体在0.6s时刻的飞行位置

由于导轨与支脚间存在间隙，会使得导弹在发射过程中，产生较大的随机扰动力.为探究此扰动力对弹体飞行的影响，求解获得间隙值为0.2mm、0.4mm和1mm情况下，弹体在0.6s时刻时的相对位置变化，如图10所示.

图10 不同间隙下弹体在0.6s时刻的飞行姿态Fig.10 Flight attitude of the projectile body in different gaps at t=0.6s

当弹架间隙为0.2mm时，Y向的飞行高度最大差值为0.73m，弹架间隙为0.4mm时，Y向的飞行高度最大差值为1.36m，弹架间隙为1.0mm时，Y向的飞行高度最大差值为4.06m；弹架间隙过大，引起的随机扰动力越大，导致弹体在飞行过程中位置不易确定，导致弹体出现较大的发射散布问题.

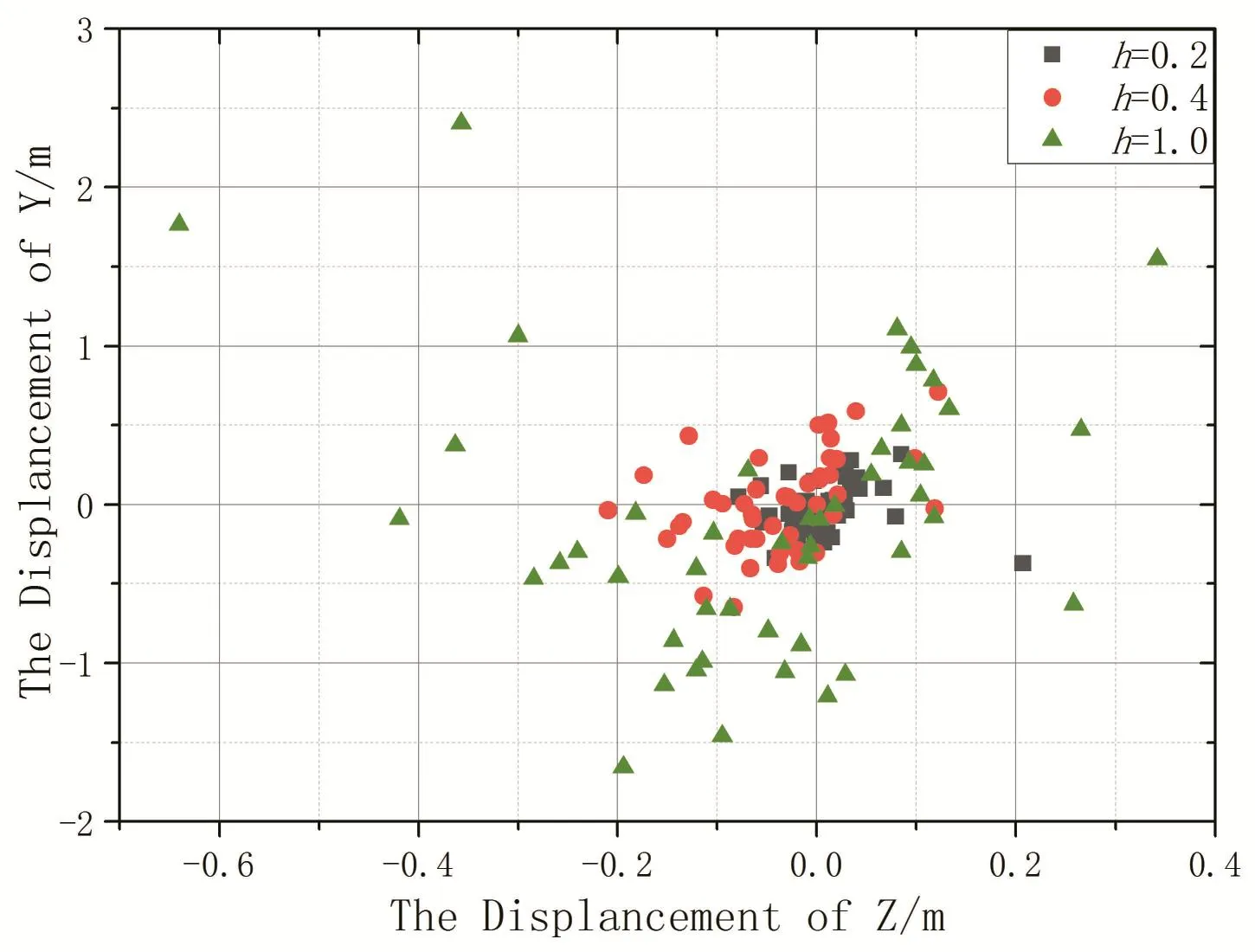
图11 不同弹架间隙下弹体在0.6s时刻飞行位置对比Fig.11 The flight statuses of the projectile body with different clearances at t=0.6s

4 小结

本文提出了随机扰动激励与多体动力学相结合的计算方法，并以含发射架的导弹发射系统为实例，对模型的计算结果进行分析，为以后相关的弹架间隙扰动计算问题提出新的参考.具体结论如下：

（1）弹架间隙的大小对弹体的飞行姿态有着较大的影响.弹架间隙越大，会使得弹体的飞行俯仰角和攻角减小，飞行轨迹减低，易出现弹体掉落的现象.

（2）弹架间隙的大小对弹体的飞行姿态有着重要的影响.弹架间隙过大，引起的随机扰动力越大，会导致弹体在Y向和Z向产生较大的偏差，会引起导弹在发射过程中的散布效应.

（3）通过对含发射架的导弹发射实例分析，当弹架间隙设置在0.2mm-1.2mm之间时，在0.5s时刻，俯仰角的最大差值为4°，在0.6s时刻，攻角差值为1.2°；当弹架间隙为1.0mm时，Y向的飞行高度最大差值为4.06m.

论文采用的方法可为研究弹架间隙对发射扰动的影响提供有效的途径，也可以为同类导弹初始扰动的分析提供参考和借鉴.