编队航天器构型重构过程中的期望轨迹跟踪控制*
2021-05-18刘建彪冯刚陈记争
刘建彪 冯刚 陈记争
(上海宇航系统工程研究所,上海201109)
引言
编队航天器是指多颗航天器根据任务需求按一定构型组成编队,通过内部各组员航天器相互合作,在功能和控制是上形成一颗“虚拟航天器”[1].编队航天器在轨飞行时,需要对编队构型进行重构,以应对其在多重任务之间的转换.因此构型重构控制在多星编队执行任务过程中十分重要,而此过程中对控制系统的要求除了能达到直接目的外,还对燃耗、快速性、安全性、稳定性甚至智能特性等提出了更高的要求,在此方面的研究在国内外十分常见,成果非常显著,主要有脉冲推力机动[2]、最优燃料控制[3]、非线性反馈控制[4]、滑模变结构控制[5]、LQR最优调节器控制[6]等等 .但是以上控制方法在解决编队航天器的构型重构控制问题,均是从渐进镇定角度出发,以消减实际运动轨迹与期望轨迹的误差来实现航天器对标称转移轨迹的跟踪,鲜有文献从渐进跟踪角度出发解决此类问题.
本文针对编队航天器构型重构过程中对安全性和稳定性的要求,基于模型参考输出跟踪理论,以航天器相对轨道动力学模型为被控对象,将期望轨迹作为参考模型,设计了一种使被控对象渐进跟踪参考模型的控制律,通过理论分析证明了该控制器的合理性,并给出了相关参数的求解方法;最后通过仿真表明,此控制器性能优良,具有一定的理论研究与工程应用价值.工程实际中可通过合理设计参数使得跟踪误差小,同时保证推力满足工程实际限制.
1 模型参考输出跟踪理论
模型参考输出跟踪控制是指通过设计一个合理的控制律使得被控对象的某些或者全部状态能够在一定时间内渐进跟踪参考模型的状态.对于给定如下状态空间表达式所表示的被控对象

以及参考模型

若存在一个控制律,使被控对象的输出yp(t)渐近跟踪参考模型输出的参考信号ym(t),即
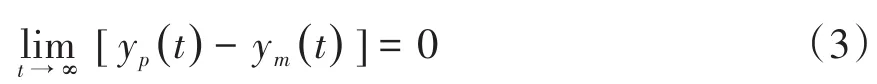
则该控制律是参考模型和被控对象的状态组合[7],即
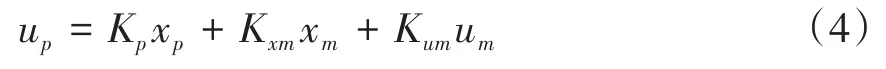
其结构如图1所示.模型参考输出跟踪问题的控制律并不总是存在的,为了推导该控制律的适用条件,这里记
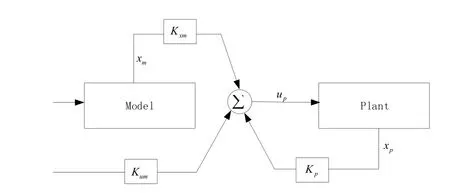
图1 模型参考输出跟踪控制器结构示意图Fig.1 Model reference output tracking framework
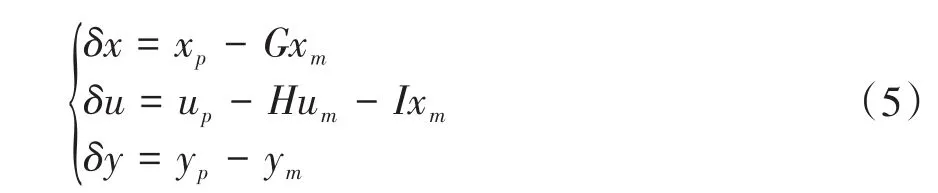
则有
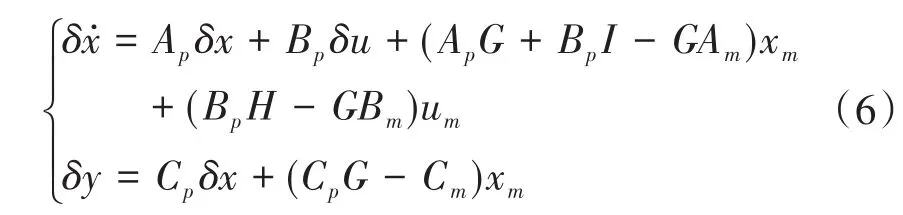
于是当有下式成立时
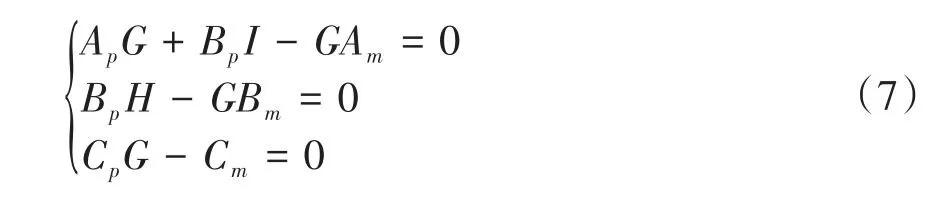
式(6)可以化简为

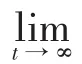
将被控对象的状态反馈镇定增益矩阵带入式(4)中,得到控制器的控制律:

于是可知,设计模型参考跟踪控制器的关键在于Kp、G、H以及I的求解.首先通过被控对象和参考模型判断G、H以及I是否存在并进行求解;然后运用特征结构配置方法或者LQR最优控制理论求解满足条件的状态反馈律Kp.
2 数学模型
编队航天器构型重构过程中,既要求各组员航天器快速准确的到达空间期望相对位置,同时也需要规划组员航天器的安全转移路径以规避碰撞危险.根据MROT理论,若将编队航天器相对运动动力学方程作为被控对象,以合理规划的期望轨迹作为参考模型,则可以实现组员航天器实际运动对期望轨迹的渐近跟踪,进而可以保证重构过程中各航天器的安全性.
2.1 被控对象
在对编队航天器相对运动进行分析时,可以不失一般性的假设编队飞行的航天器只有两颗,其中描述航天器相对运动时作为参考基准的航天器称为目标航天器,自由运动的航天器称为追踪航天器,如图2所示.两航天器在惯性坐标系中的位置矢量分别为rD和rS,则两航天器的相对位置矢量为:
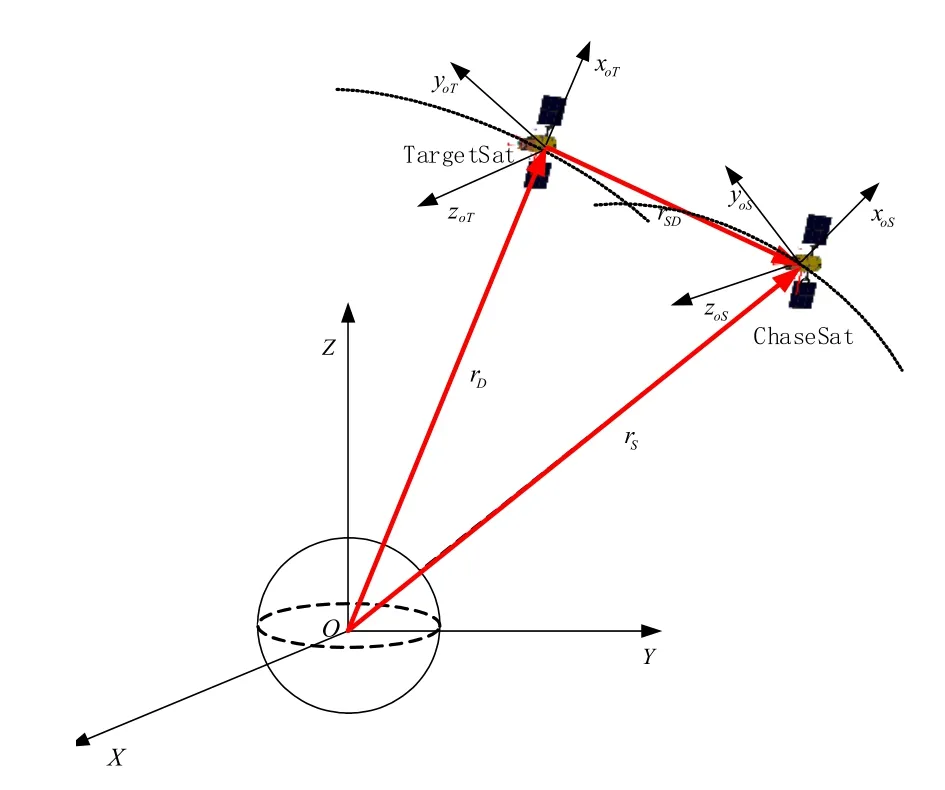
图2 相对运动示意图Fig.2 Relative motion diagram

在惯性坐标系下,目标航天器和追踪航天器的轨道动力学方程可表示为:

式中,μ为地球引力常数;f表示除地球中心引力之外的所有摄动力和控制输入引起的加速度.于是两航天器的相对轨道动力学方程为:

将其转化为在目标轨道坐标系(LVLH)中的表达形式:
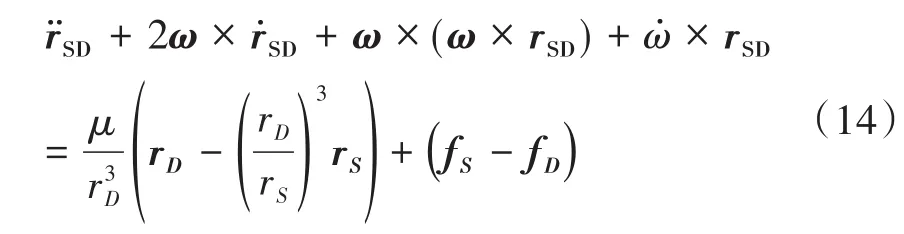
式中,ω为目标航天器轨道坐标系相对惯性坐标系的转动角速度[8].将上式简单整理可得相对运动方程的分量形式:

式中,θ表示目标航天器的真近点角.
若两颗编队航天器运行轨道为近圆轨道且相距很近时,其轨道要素差别较小,因此可以采用如下的线性方程描述两航天器的相对运动[9]:

式中,n为目标航天器的平均角速度.
2.2 参考模型
为了便于控制器设计,需对期望轨迹进行数学描述,进而可以转化为状态空间表达式表示的参考模型.根据始末时刻或者过程中的状态约束,采用多项式插值定理来确定期望轨迹的数学描述f(x,t,κ).f(x,t,κ)为具有空间物理运动规律一般特性的时变函数,其中x表示航天器的期望状态,t表示时间,κ表示运动状态无关的其他状态变量[10].
编队航天器的相对远动轨迹几乎都可以看作是3个典型模式(直线逼近、定点悬停以及快速绕飞)的组合.针对直线逼近和悬停过程,标称轨迹的数学描述为始末位置、速度、加速度以及其它阶导数的函数;针对快速绕飞过程,可先将绕飞矢径在目标轨道坐标系中的高低角θ和方位角φ作为变量,采用多项式插值定理来确定其数学描述f(θ,φ,t,κ).然后通过空间几何关系,如图3所示,转化为在目标轨道坐标系下两航天器相对位置的数学描述f(x,t,κ).
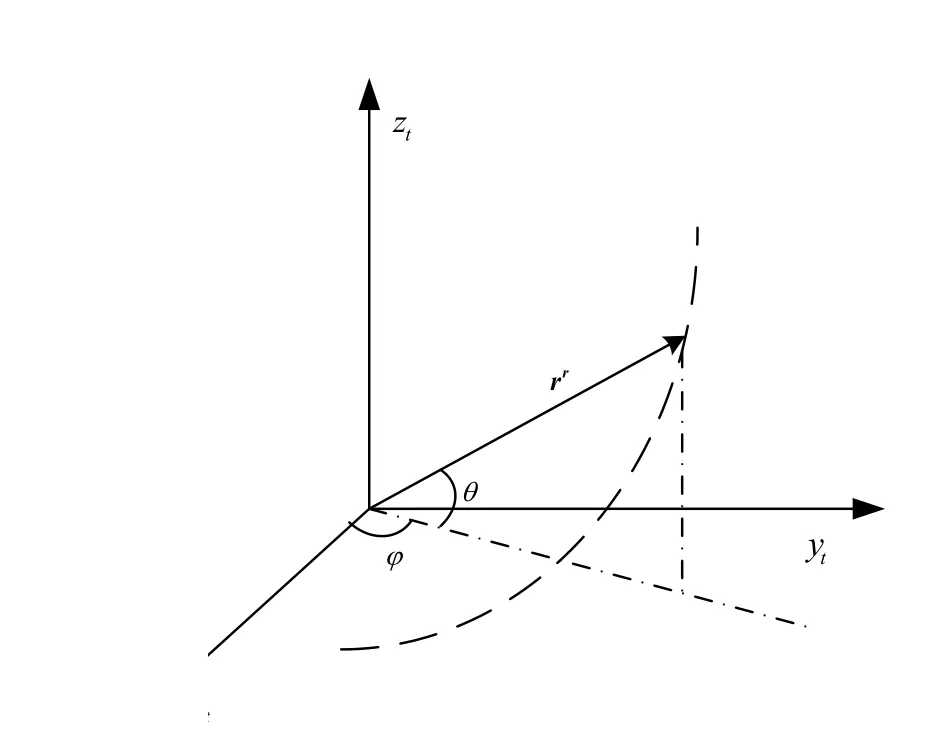
图3 绕飞轨迹在目标轨道坐标系下的示意图Fig.3 Schematic diagram of the fly-around trajectory in the target orbit coordinate system
分析可知,描述构型重构过程中编队航天器的相对运动标称轨迹均可设计为仅受加速度项驱动的双积分系统,因此各阶段的参考模型均可表示为式(17),区别仅在于加速度项.
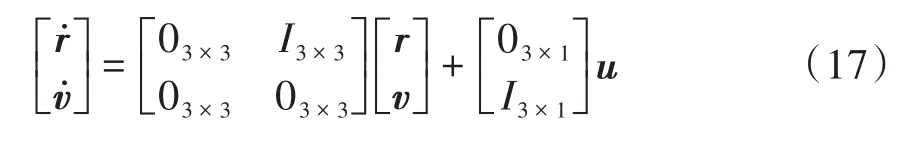
3 仿真验证
以近圆GEO轨道编队飞行的两颗航天器为例,针对如下具体飞行流程,进行仿真验证.
1)直线逼近:追踪器从目标器后方3km处逼近至目标器下方60m处,限时1h;
2)定点悬停:追踪器在目标器下方60m处与目标器保持相对静止,限时30min;
3)快速绕飞:追踪器从目标器下方60m处作轨道面内圆轨迹绕飞至目标器上方60m保持相对静止,限时30min.
采用二次多项式描述各飞行流程的期望轨迹,其中直线逼近阶段的加速度项可以设计为:
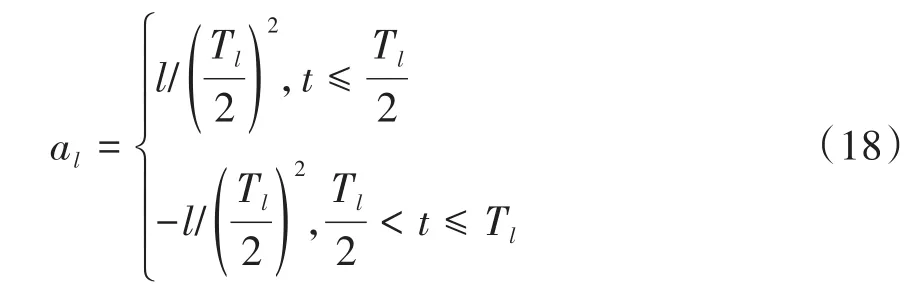
式中,al表示直线段加速度,其方向由逼近起点指向逼近终点,l为逼近总距离,Tl为所用时间.悬停阶段的标称轨迹加速度项可以设计为ah=0表示整个悬停过程中两航天器无相对运动趋势.快速绕飞阶段的标称轨迹加速度项可以设计为:
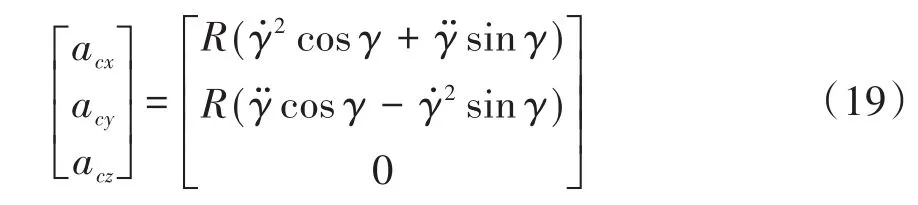
式中,acx,acy以及acz表示目标轨道系下的三轴加速度,R表示绕飞轨迹半径,γ,γ̇以及γ̈表示绕过的角度、角速度以及角加速度.
利用特征结构配置理论,将系统的闭环极点配置为在左半平面靠近原点,得到各个增益矩阵分别为:
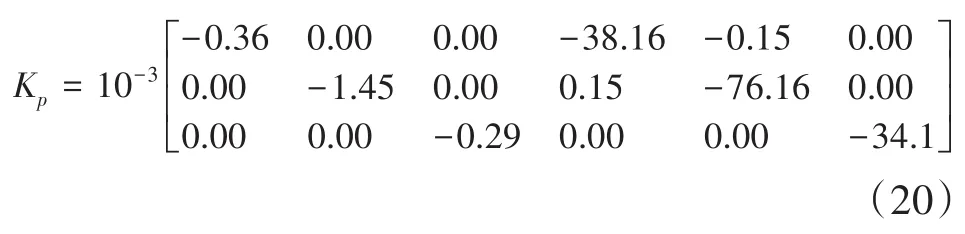
进而可得

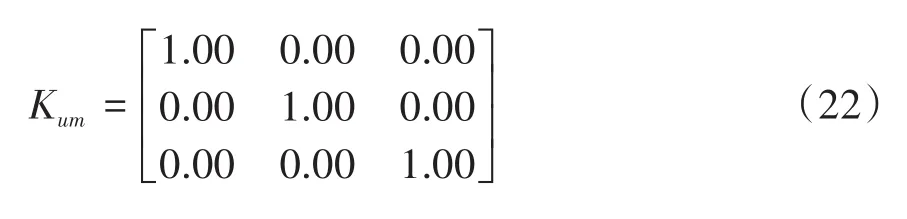
基于表1所列的追踪航天器和目标航天器的初始轨道根数开展仿真验证.图4至图7给出了追踪航天器在目标航天器轨道坐标系中依次实现直线逼近、定点悬停、圆轨道快速绕飞等飞行流程的仿真结果.

表1 两航天器的初始轨道根数Table 1 Initial orbital number of two spacecraft

图4 追踪器在目标器轨道坐标系下的运动轨迹Fig.4 Trajectory of the tracker in the orbital coordinate system of the target
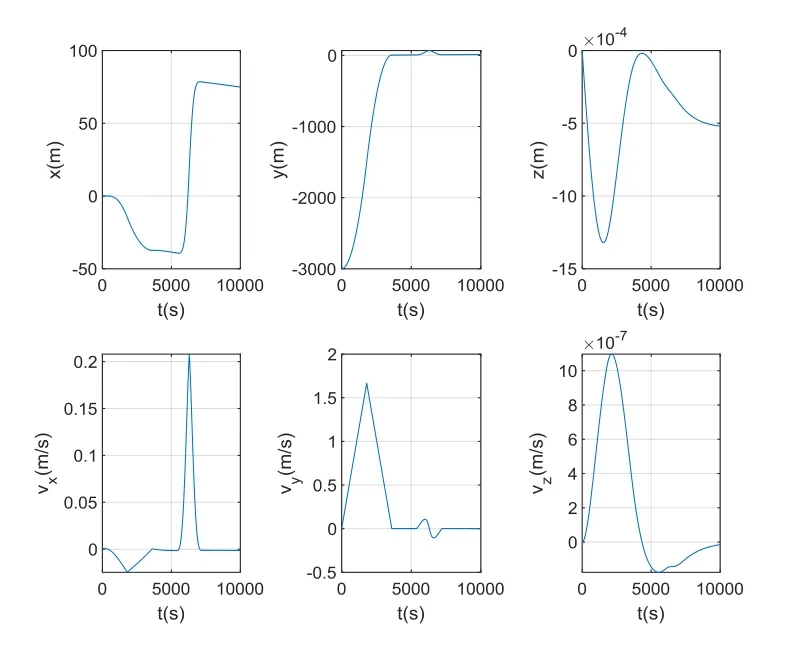
图5 追踪器在目标器轨道坐标系的状态变化曲线Fig.5 The state curve of the tracker in the target orbital coordinate system

图6 追踪器实际轨迹与期望轨迹的误差Fig.6 Trajectory errors of the tracker between the real and desired ones
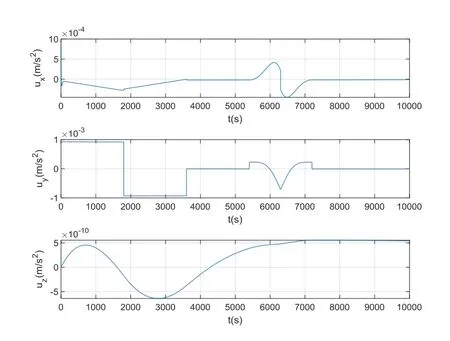
图7 追踪器控制输入变化曲线Fig.7 Tracker control input curve
对仿真结果进行分析可知,基于模型参考输出跟踪控制理论设计的控制器跟踪精度高,稳定性好,推力满足工程实际限制.
4 总结
本文从模型参考输出跟踪理论出发,针对编队航天器构型重构过程中有期望轨迹约束的轨道控制问题,设计了一种将被控对象的状态反馈和参考模型的状态前馈结合的组合控制器.仿真表明,该控制器性能优良,误差收敛快,跟踪精度高,对工程实际具有一定指导意义,但是由于在仿真过程仅考虑了J2摄动影响,并未对真实工况下外界干扰以及导航误差的影响进行分析,所以后续将继续深入研究以验证此控制器的实用性.
