例谈同构视角下函数与导数高考试题的求解策略
——从2020年高考试题谈起
2021-05-18云南师范大学信息学院650500唐明超广东省佛山市顺德区容山中学515800潘敬贞广东省佛山市实验学校高中部528000袁锦前
云南师范大学信息学院 (650500) 唐明超广东省佛山市顺德区容山中学 (515800) 潘敬贞广东省佛山市实验学校高中部 (528000) 袁锦前
高考中函数与导数试题多以压轴题的形式呈现,具有较强的灵活性,重在考查学生的数学抽象与逻辑推理核心素养,检测学生的四基与四能发展水平,试题往往具有较好的区分度.但是变化的试题背后总有一些不变的元素以及解决问题的基本方法.文章从研究2020年的部分函数与导数试题出发,探究试题背景,分析试题命题意图,基于同构的视角谈解决该类问题的基本做法.
所谓同构,就是根据问题解决需要寻找与之紧密关联的特殊函数,将关联函数的基本性质进行迁移并运用于问题解决的过程.同构的目的在于从特殊到一般,经历问题的合理转化将看似复杂的问题简单化,抽象的问题模型化.用好同构思想解题可以省去部分常规解法中必须经历的求导或者分类讨论的复杂过程,简化推理步骤,优化数学运算.同构往往涉及到指数与对数的转化,切线放缩,整体换元等过程,是解决多个基本初等函数复合问题的重要手段,主要运用于解决比较大小,零点存在性问题,不等式恒成立求参数的取值范围等问题中.
一、比较大小
例1 (2020年课标全国Ⅱ卷理11题)若2x-2y<3-x-3-y,则( ).
A.ln(y-x+1)>0 B.ln(y-x+1)<0
C.ln|x-y|>0 D.ln|x-y|<0
分析:试题是不等式比较大小的经典问题,解决关键在于抽象出不等式背后所隐藏的函数,解题的基本方法是先观察式子的结构特点,将不等式进行适当整理化归,寻找一个符合式子结构特点的特殊函数,通过研究关联函数的单调性、最值等基本性质进而实现对原问题的解答.
解析:从未知数统一的角度将式子转化为2x-3-x<2y-3-y,发现不等式两边的结构相同而且符合函数f(t)=2t-3-t的基本形式,成功找到了关联函数;容易判断关联函数f(t)=2t-3-t的单调性为增函数,所以由f(x) 例2 (2020年课标全国Ⅰ卷理12题)若2a+log2a=4b+2log4b,则( ). A.a>2bB.a<2bC.a>b2D.a 分析:试题呈现的是一个等式,要求判断未知数的大小关系,如果考虑用特殊值法来判断则不容易找到符合条件的特殊值.所以解决该问题的基本思路首先还是考虑同构,即观察式子的结构特点,寻找符合式子结构特点的函数,进而研究函数的性质. 解析:将式子适当变形得2a+log2a=22b+log22b-1,观察式子结构特点,容易找到符合条件的函数f(x)=2x+log2x,且f(2b)-f(a)=1>0;又因为函数是增函数,所以2b>a,故选B. 分析:试题考查导数与三角函数的综合问题,考查学生运用导数研究函数单调性及最值问题的基本技能.试题设计层级递进,虽然第(2)小题为第(3)小题搭好脚手架,但是(3)题不等式的证明抽象性较强,难度较大.如能用好同构思想对不等式进行适当变形,将其转化成与第(2)题结论相关联的结构则可以快速得出证明. 例4 (2020年课标全国Ⅰ卷文20题)已知函数f(x)=ex-a(x+2).(1)当a=1时,讨论f(x)的单调性;(2)若f(x)有两个零点,求a的取值范围. 分析:该题属于函数与导数综合问题,第(1)题研究确定函数的单调区间,意在考查学生的基础知识与基本技能.能准确求导是前提,掌握导函数与原函数的逻辑关系是关键.第(2)题考查零点与参数的取值范围问题,零点个数确定,要求参数a的范围,解决该类问题一般有三个基本思路可以尝试. 思路2:如果不分离参数,可直接对f(x)求导,再对参数a进行分类讨论,通过研究函数极值或最值的符号确定参数a的取值范围. 思路3:同构的思想,即通过观察式子结构特点寻找与之相近的常见函数或者不等式,通过研究同构函数或不等式的性质间接得出答案,解法如下. 特别说明:为满足逻辑推理的严谨性,运用不等式ex≥x+1之前需要给予严格证明.可以构造f(x)=ex-x-1,所以f′(x)=ex-1,因为f′(0)=e0-1=0且f′(x)=ex-1在x∈R上单调递增,所以当x∈(0,+∞)时f′(x)>0,即f(x)单调递增;当x∈(-∞,0)时f′(x)<0,即f(x)单调递减,所以f(x)min=f(0)=0,即f(x)=ex-x-1≥0,所以ex≥x+1恒成立. 例5 (2020年浙江卷22题第(1)问)已知1 分析:要证明函数在区间上有唯一零点,等价于证明函数在区间上有唯一的实数根或者图象与x轴有唯一的交点,当然也可以考虑将函数分割成两个恒等的基本初等函数,证明图象有唯一的交点.函数f(x)包含了g(x)=ex与h(x)=x+a两个基本元素,容易联想到同构式ex≥x+1恒成立,且取等号的条件为x=0. 解析:令f(x)=ex-x-a=0得ex=x+a,因为1 例6 (2020年新高考全国Ⅰ卷21题第(1)问)已知函数f(x)=aex-1-lnx+lna.若f(x)≥1,求a的取值范围. 分析:解决不等式恒成立问题主要有三个基本策略,一是通过研究函数的单调性确定函数在给定区间上的取值范围;二是将不等式拆分成两部分,分别求其最大值与最小值进行比较;三是利用同构思想合理使用切线放缩进行证明.函数f(x)=aex-1-lnx+lna中既包含了指数,也含有对数,是较复杂的复合函数问题,可以优先考虑通过指对数互化构造新函数实现对问题的解答,具体过程如下. 解析:由f(x)=aex-1-lnx+lna≥1得elna+x-1-lnx+lna≥1,考虑构造相同的式子结构得elna+x-1+lna+x-1≥lnx+x=elnx+lnx,等价于et1+t1≥et2+t2,可以构造函数g(x)=ex+x,则不等式等价于g(lna+x-1)≥g(lnx);又因为g(x)为单调增函数,不等式等价于lna+x-1≥lnx,即lna≥lnx-x+1恒成立.又因为ex≥x+1(x≥0)等价于x≥ln(x+1),也等价于x-1≥ln(x-1+1)即x-1≥lnx,所以lnx-x+1≤0,要使得lna≥lnx-x+1恒成立,只需(lna)min≥(lnx-x+1)max,即lna≥0,从而a≥1. 试题1 (2017年新课标全国Ⅱ卷理21题第(1)问)已知函数f(x)=ax2-ax-xlnx,且f(x)≥0,求a. 分析:该题也是不等式恒成立求参数的取值范围问题,观察式子结构特点容易联想到同构不等式ex≥x+1及其变形.所以由函数f(x)=ax2-ax-xlnx≥0得x[a(x-1)-lnx)≥0,等价于a(x-1)-lnx≥0,即lnx≤a(x-1)①;又因为ex≥x+1(x≥0)等价于x≥ln(x+1),也等价于x-1≥ln(x-1+1)即x-1≥lnx②,由①②两式得a=1. 分析:(1)该题也是考查不等式的恒成立问题求参数的取值范围问题,由式子结构特点容易想到同构不等式ex≥x+1及其变形.依题意可得定义域为x∈(0,+∞),由f(x)=x-1-alnx≥0得x-1≥alnx①,又因为ex≥x+1(x≥0)等价于x≥ln(x+1),也等价于x-1≥ln(x-1+1),即x-1≥lnx②,由①②两式得a=1. 解题反思:如能熟练理解题目结构信息找到问题的本质,经过适当的转化就可以利用已知结论解决问题,整个解题过程思路清晰,目标明确;结合已有知识经验将原本看似复杂的问题所隐藏的数学本质挖掘出来是解决导数压轴题的关键与前提. 一类对基本初等函数进行加减乘除运算得到的形如y=xlnx,y=lnx+ax+b,y=alnx+bx+c,y=aex+bx+c,f(x)=aex-ln(x+b)等的复合函数是高考考查的热点和重点.在比较大小,零点探究,不等式证明等问题中,可以尝试基于同构的视角去寻找变化的试题背后不变的问题本质,通过对问题进行适当转化与化归,联想与之关联的函数或者不等式.比如不等式x+1≤ex及其变式ln(x+1)≤x,x∈(-1,+∞)就是解决历年高考试题的重要利器,也是高考命题的重要素材,如能准确识别它并能在解决实际问题的过程中将其灵活地运用好,可以实现简化推理并优化运算的作用.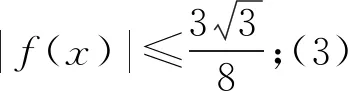
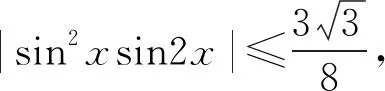
二、零点存在性问题
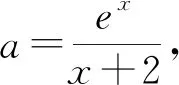
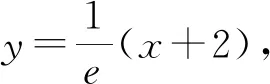
三、不等式的恒成立问题
四、高考链接