一道解析几何试题的解析及教学思考

浙江省湖州二中 (313000) 胡志杰

2020年浙江高考结束后，考生普遍认为解析几何第二问难以入手，计算量大，变元之间难转化.笔者认为2020年第21题很好地考察了学生的解析几何基本能力，是让学生理解解析几何的坐标本质，有利于培养学生数学逻辑、数学模型和数学运算等核心素养.

1 试题呈现

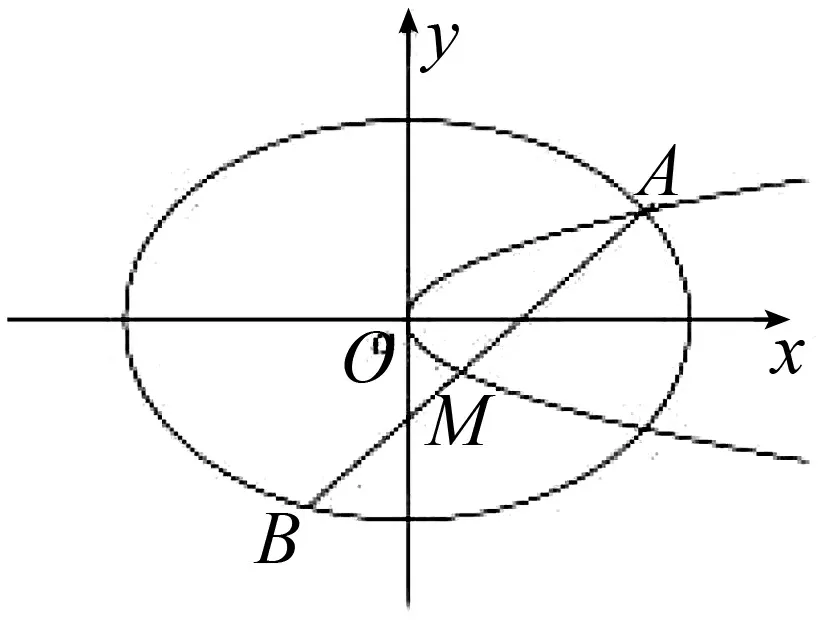
图1

C2:y2=2px(p>0)，点A是椭圆C1与抛物线C2的交点，过点A的直线l交椭圆C1于点B，交抛物线C2于M(B，M不同于A)．

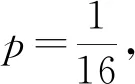
(Ⅱ)若存在不过原点的直线l使M为线段AB的中点，求p的最大值．

考点分析：本题主要考查椭圆、抛物线的几何性质、直线与圆锥曲线的位置关系、线段中点坐标等知识，同时考察了解析几何的基本思想方法、综合应用知识的能力和数学运算素养，都是高中解析几何中最核心的知识、技能、思想方法和素养.近年考题多为在抛物线中求三角形面积或面积比的取值范围，此题设计椭圆与抛物线交点以及有p的范围，平时考生在做练习卷以及各地模考卷中也没有出现过，许多考生摸不到方向，问题出在哪里，值得教师研究.

2 解法探究与评析

解析几何题在解答时，“设点”还是“设线”往往让学生难以选择.回顾近年考题，无论是“设点”还是“设线”，一般都可以解决.点、直线、曲线作为几何中的基本图形，构建起了我们研究的解析几何对象.解析几何的基本方法是坐标法，因此，我们研究解析几何图形中的众多关系，最终都是将其转化成为点的坐标、直线或曲线方程中的有关系数等变量.无论是“设点”或是“设线”的做法，运算的核心都是在建立起众多变量之间的联系，本题则是最终转化到变量p上去.

解法2：设直线l：x=λy+m(λ≠0，m≠0)，点A(x0,y0)，将直线l分别代入C1、C2方程得yM=

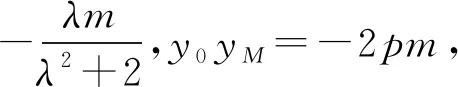
点评：以上两种解法采用得基本模型都是设线，由于涉及直线与曲线交点、椭圆与抛物线交点，所以在求解过程中必须要得到点A的坐标.不同于我们通常设直线方程后“舍而不求”，解法1通过求根公式将其解出，整个过程计算量计算量非常大；解法2通过两次韦达定理得到点A坐标，运算量相对减少，也是数学运算素养的体现，需要教师平时教学中加以训练.此法思维简洁，变量单一，考生容易入手却难于做到最后.

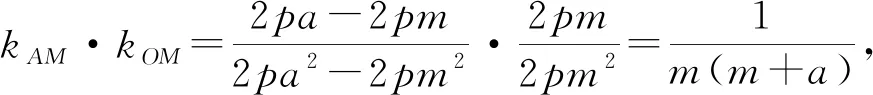
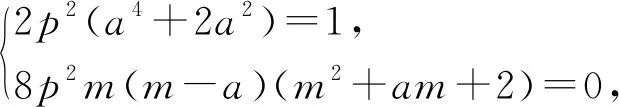
点评：以上两种解法采用得基本模型都是设点，一般来说设点相对于设线变量更多，因此对学生的运算能力要求更高，但思维能力的提升往往能带来运算量的降低.点A可用p表示，但形式并不单一，选择A(2pa2,2pa)合理避开了分式与根式，是运算素养的体现.解法3通过点差法计算kAM·kOM，能力较强的考生也可直接通过第三定义得到，大大降低了计算，节约考试时间.解法4将A、B坐标分别代入C1、C2的化简过程中，可观察到点M与点A重合时，B也与A重合，此时m=a是关于m的方程的一个增根，整理后所得的式子中必定回出现因式m-a，便为因式分解提供了方向，类似这样的运算技巧需要教师在课堂教学中不断渗透.

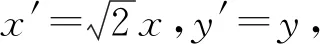
点评：此法通过伸缩变换，将椭圆化成圆，便将问题转化为只是关于直线与抛物线的问题了.关于中点M，在圆中只需通过垂径定理便可简单处理.解法5运用了转化与化归思想、数形结合思想、方程思想等，在对应思想的指导下完成了问题转化/模型构建和思路突破，思想教应成为数学课堂教学的核心，需要教师重视.

3 教学思考

3.1关注心态，明确入口

解析几何作为必考大题之一，考生的困难主要表现为思想方法不入门缺乏设点、设线的意识和能力；缺乏问题间相互转化的能力；计算能力薄弱等.而教师在复习教学时常就题论题，降低标准，更甚于根据所谓的阅卷标准进行“捞分”讲题，以至学生对解析几何的学科特点、思想方法不清晰透彻.教师应帮助学生理清解题思路，明确解题方法，过好入门关.

3.2关注解法，加强变式

“解题通法”是开展考题教学的意义所在，因此在完成思路突破后有必要引导学生贯通考题的整体思路，对解题的关键点、有价值的内容进行回顾总结，并通过考题变式的方式来加深学生对问题的理解．教师在教学中要帮助学生树立坐标思想、强化数形意识、巧用几何方法，以达到事半功倍的效果.

3.3关注运算，提升素养

数学运算是解析几何的重要核心素养之一，也是学好解析几何的重要保证.教学在日常教学中要逐步引导学生分析运算条件、理解运算对象提供正确的思维方式，保证运算方向的正确性和运算方法的合理性，切不可只重视算法形成而不愿放慢脚步引导学生完成运算步骤，把计算过程留于课后.课堂内学生运算得不到训练，不仅导致算法不好，计算能力差，费事费力，更重要的是降低考生考试效率，影响考试心态，从而出现事倍功半的恶性循环.