变式探究，类比迁移——由一道调研题引发的思考

安徽省芜湖市第一中学 (241000) 刘海涛

数学中的变式指的是有目的，有计划地对命题进行合理转化，从而揭示问题本质，达到举一反三的效果.本文中笔者对一道高三的调研题的变式进行探究和类比推广，现与读者分享.

1.问题呈现

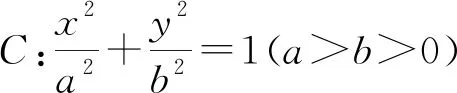
(1)求椭圆C的方程；

(2)若A(-2,0),B(2,0),M(4,1)，直线MA与椭圆C的另一个交点为点P,直线MB与椭圆C的另一个交点为点Q,求证：直线PQ恒过定点.

该题是直线和椭圆位置关系的解析几何综合题，第一问较为容易，第二问考查了直线与椭圆位置关系，韦达定理，直线过定点等知识，需要学生有一定的运算能力和综合分析问题的能力.

2.问题解决

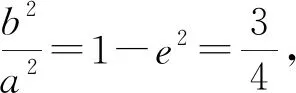
思考：美国数学教育学家波利亚说过：“观察可以导致发现，观察将提示某种规则、模式或定律.”此题的第二问具有很好的探究价值，笔者通过观察、分析、联想发现本题可以进行一般化推广.

3.变式探究

(1)注意到点A,B是长轴的两端点，点M在右准线上，定点(1,0)是右焦点，将椭圆方程一般化，可得到性质1.

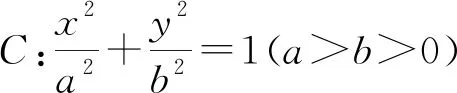
(2)将点M换成一般情况，即点M是准线上的动点，通过探究得性质2.

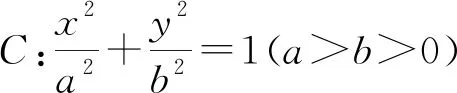
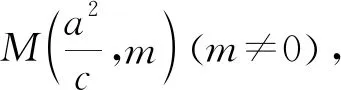
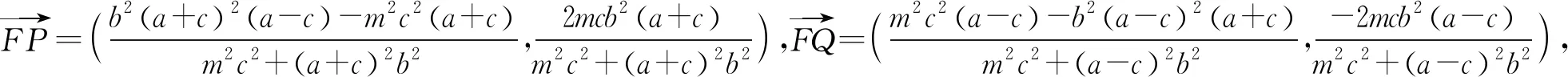
(3)将命题2中的部分条件和结论互换，通过变式探究，得到性质3和性质4.

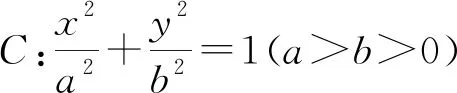
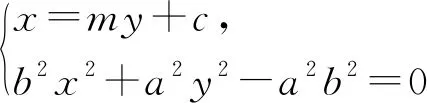
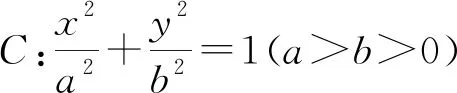
证明过程省略，可参考性质2和性质3的证明方法.

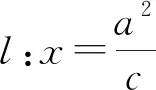
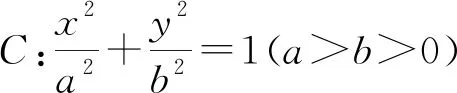
4.类比迁移

圆锥曲线不限于椭圆，还有双曲线和抛物线，基于上述探究，笔者借助几何画板探究双曲线发现也有类似上述结论.

这里证明与椭圆类似，过程省略.

我们知道抛物线没有两个顶点，那么我们还是否有类似命题呢？笔者借助几何画板探究发现了结论3.

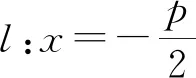
下面仅给出由①②推出③的证明过程，另两种情况的证明过程类似可得.

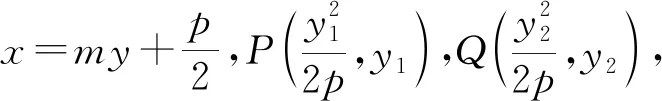
5.结语

“学而不思则罔，思而不学则殆”，在数学学习中面对一道问题时，我们不能单纯为了得到答案去解题，而应该去深层次挖掘题目本质，变式探究出一般性结论，掌握探究问题的规律方法，并进行类比迁移，到达“解一题，通一类”的目的.