三角形中与角有关的几个等式

广东省中山纪念中学 (528454) 邓启龙

首先给出本文要用到的引理.

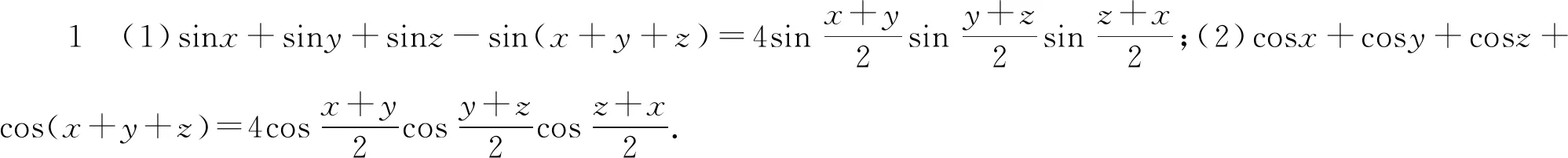
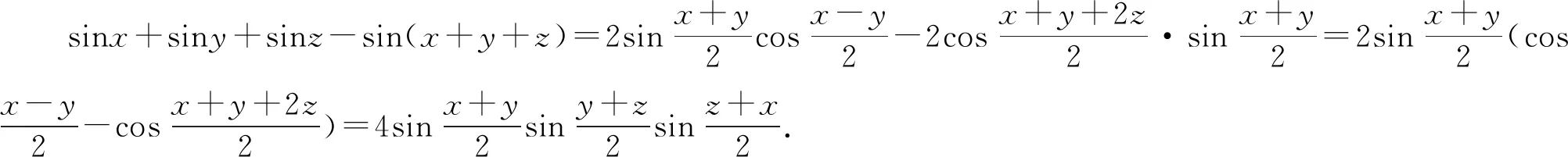
(2)证明与(1)类似.

设△ABC的三个内角分别为A,B,C,接下来给出几个与角A,B,C有关的等式.

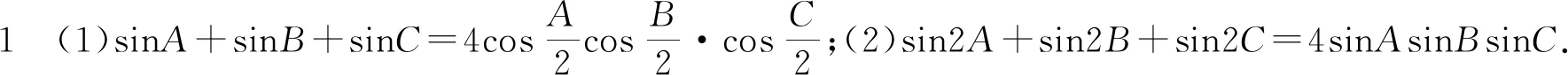
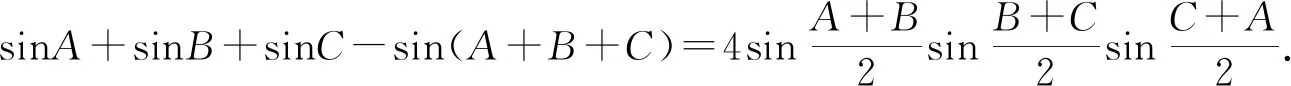
由A+B+C=π得sinA+sinB+sinC=

(2)证明与(1)类似.

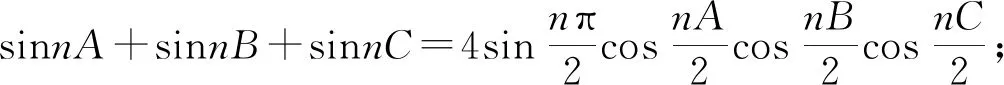
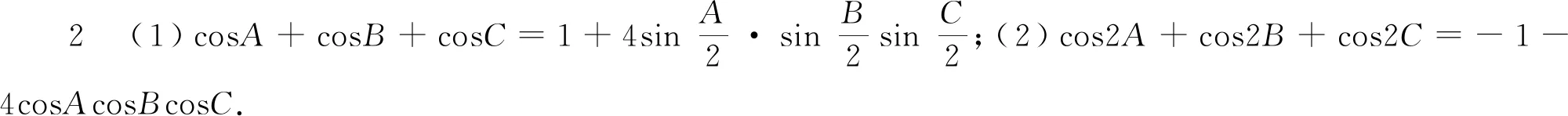
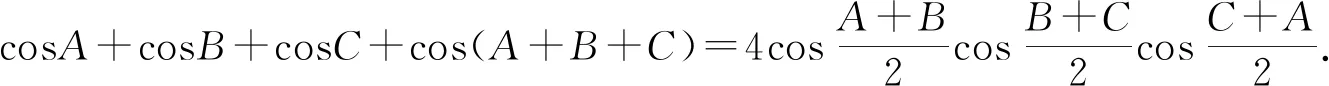
(2)证明与(1)类似.

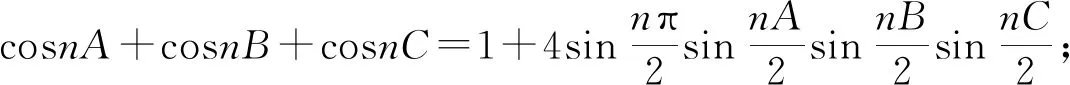
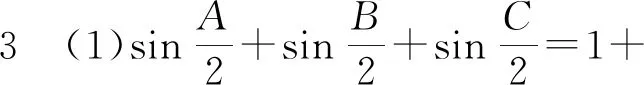
等式4 (1)sin2A+sin2B+sin2C=2(1+cosAcosBcosC)；(2)cos2A+cos2B+cos2C=1-2cosAcosBcosC.

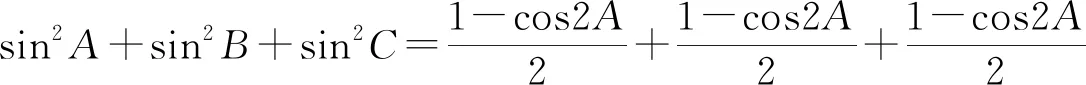
=2(1+cosAcosBcosC).

(2)证明与(1)类似.

等式5 (1)tanA+tanB+tanC=tanAtanBtanC；(2)cotAcotB+cotBcotC+cotCcotA=1.

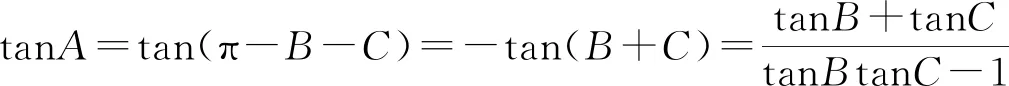
(2)(1)式两边同时除以tanAtanBtanC得cotAcotB+cotBcotC+cotCcotA=1.

注：(1)tanA+tanB+tanC=tanAtanBtanC是三角形中常用的性质.(2)任意整数n,有tannA+tannB+tannC=tannAtannBtannC,cotnAcotnB+cotnBcotnC+cotnCcotnA=1.

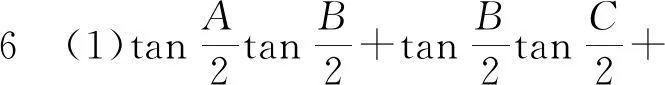
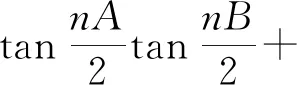
等式7 (1)sin2A=sin2B+sin2C-2sinBsinCcosA；(2)sin2A+sin2B+sin2C=2sinAsinBcosC+2sinBsinCcosA+2sinCsinAcosB；

(3)sinAsinBcosC+sinBsinCcosA+sinCsinAcosB=1+cosAcosBcosC；(4)sinAcosBcosC+sinBcosCcosA+sinCcosAcosB=sinAsinBsinC.

证明：(1)sin2B+sin2C-2sinBsinCcosA=sin2B+sin2C+2sinBsinCcos(B+C)=sin2B+sin2C+2sinBsinC(cosBcosC-sinBsinC)=sin2B+sin2C+2sinBsinCcosBcosC-2sin2Bsin2C=sin2B(1-sin2C)+sin2C(1-sin2B)+2sinBsinCcosBcosC

=sin2Bcos2C+sin2Ccos2B+2sinBsinCcosBcosC

=(sinBcosC+sinCcosB)2=sin2(B+C)=sin2A.

(2)由(1)得sin2A=sin2B+sin2C-2sinBsinCcosA.同理可得sin2B=sin2C+sin2A-2sinCsinAcosB,sin2C=sin2A+sin2B-2sinAsinBcosC,以上三个式子相加即得(2).

(3)由(2)和等式4(1)即得.

(4)sinAcosBcosC+sinBcosCcosA+sinCcosA·cosB=cosC(sinAcosB+sinBcosA)+sinCcosAcosB=cosCsin(A+B)+sinCcosAcosB=sinC(cosC+cosAcosB)=sinC[cosAcosB-cos(A+B)]

=sinAsinBsinC.

注：sin2A=sin2B+sin2C-2sinBsinCcosA是余弦定理的等价形式,本文只从三个内角的关系出发来证明该等式.

下面结合例题说明这些三角形中与角有关的等式在三角形中的应用.

例1 △ABC的三边分别为a,b,c,面积为S,p为半周长,外接圆半径为R,证明:

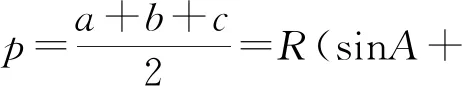
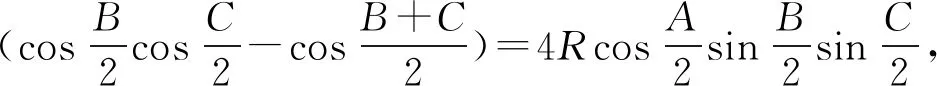
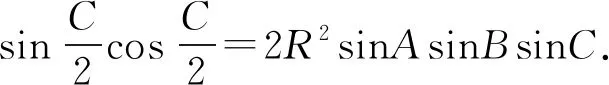
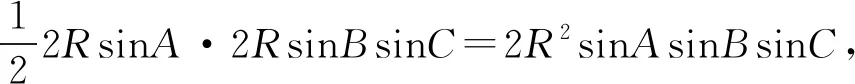
注：由正弦定理将三角形的三条边化成角,然后利用三个内角的等式证明海伦公式.

例2 △ABC的三边分别为a,b,c,p为半周长,外接圆半径为R,内切圆半径为r,证明:

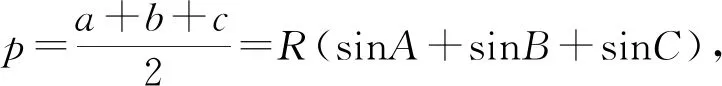
(2)由(1)的证明易得.

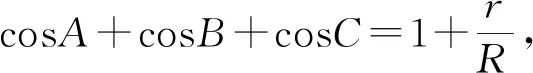
例3 △ABC的三边分别为a,b,c,外接圆半径为R,内切圆半径为r,证明:

(1)acosA+bcosB+ccosC=4RsinAsinBsinC;

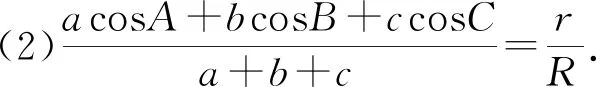
证明：(1)由等式1(2)得acosA+bcosB+ccosC=2RsinAcosA+2RsinBcosB+2RsinCcosC

=R(sin2A+sin2B+sin2C)=4RsinAsinBsinC.

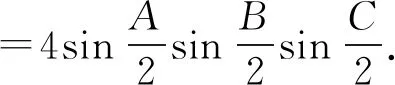
例4 △ABC的三个内角分别为A,B,C,证明:

(1)cotA+cotB+cotC=cotAcotBcotC+cscAcscBcscC;(2)tanAtanB+tanBtanC+tanCtanA=secAsecBsecC+1.

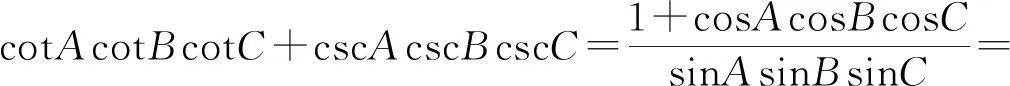
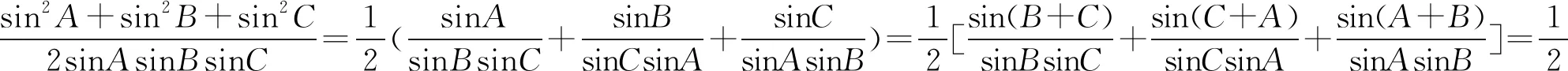
=cotA+cotB+cotC.

(2)由(1)得cotA+cotB+cotC=cotAcotBcotC+cscAcscBcscC,两边同时除以cotAcotBcotC得tanAtanB+tanBtanC+tanCtanA=secAsecBsecC+1.