“隐零点”问题三探

浙江省绍兴稽山中学 (312000) 韩 琦

1.一探基本思路

例1 已知函数f(x)=ex-ln(x+2),证明f(x)> 0.

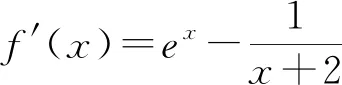
从上可以看出，处理“隐零点”问题思路是：

(1)用零点存在性定理判定导函数零点的存在性，列出零点方程f′(x0)=0，并结合f(x)的单调性得到零点的范围；

(2)以零点为分界点，说明导函数f′(x)的正负，进而得到f(x)的最值表达式；

(3)将零点方程适当变形，整体带入最值式子进行化简证明.

2.二探深化思想

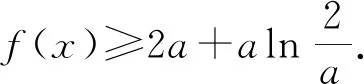
分析：对含参的函数f(x,a),(a为参数)“隐零点”问题, 同基本思路，不妨设方程f′(x,a)=0的根为x0,但要注意确定这个x0的合适范围,这个也往往和a的范围有关.事实上，把“隐零点”问题转化为“显零点”问题也是很好的方法.

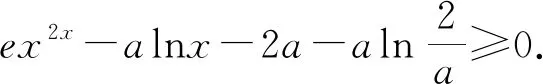
3.三探变异思维

例3 (2013全国新课标卷Ⅱ-21-2)已知f(x)=ex-ln(x+m).(1)设x=0是f(x)的极值点，求m，并讨论f(x)的单调性；(2)当m≤2时，证明f(x)> 0.

解：(1)略；(2)当m≤2时，x∈(-m,+∞) ，ln(x+m)≤ln(x+2)，从而ex-ln(x+m)≥ex-ln(x+2)，故只需证明h(x)=ex-ln(x+2)>0 即可.

参照例1解答过程，即可得证.

评注：本例就是把问题通过放缩等数学方法演变成“隐零点”问题，然后求解.

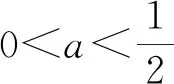
评注：本题的难点在于找到零点x0与a的联系.利用解决“隐零点”问题的思路,可以较好地把问题化难为易,化繁为简.