一道高三期中试题的解法探究
2021-05-18浙江省衢州第二中学324000
中学数学研究(江西) 2021年5期
浙江省衢州第二中学 (324000) 刘 琼
一、试题呈现
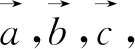
二、解法探究
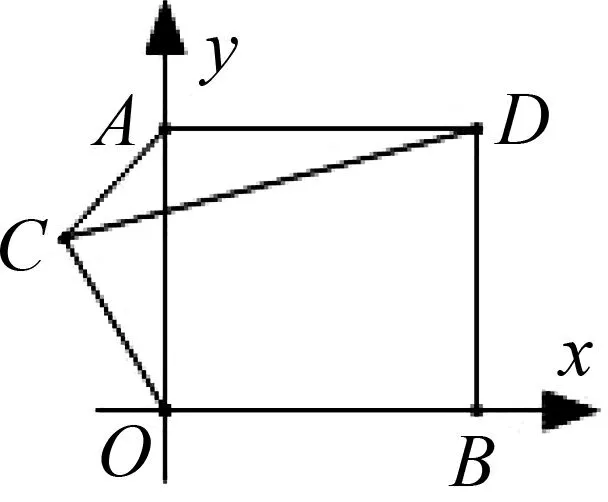
图1
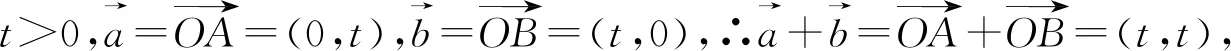
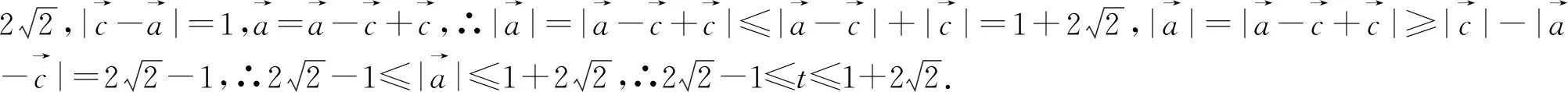
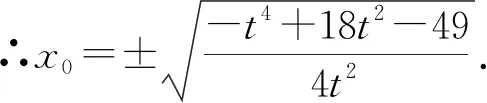
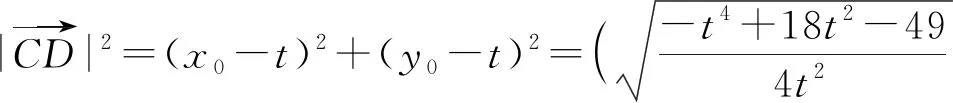
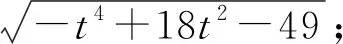
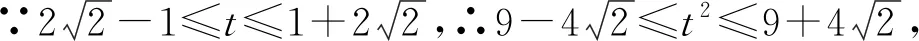
点评:解法1通过建立平面直角坐标系,运用坐标运算求解,方法直接自然,但计算过程比较繁琐.我们在教学过程中,也需要引导学生通过适量的运算训练,促进数学思维的发展,形成规范化思考问题的品质,养成一丝不苟、严谨求实的科学精神.
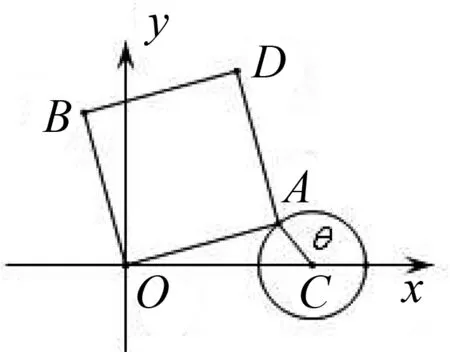
图2
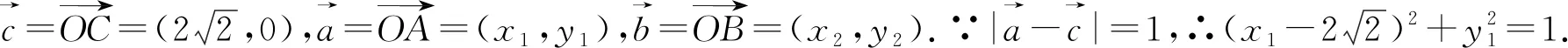
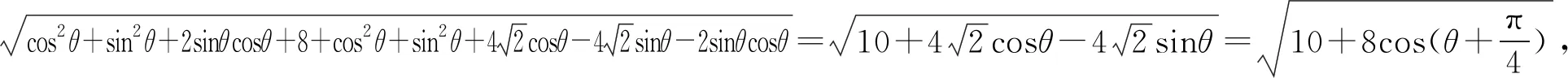
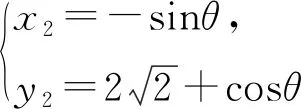
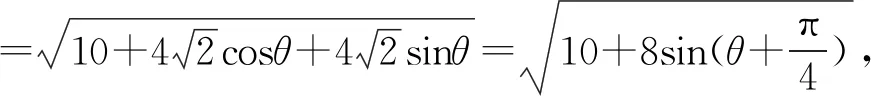
点评:解法2巧妙地建立了平面直角坐标系,又富有想象力地从圆的参数方程的视角处理点A和点B的坐标,方法新颖独到.
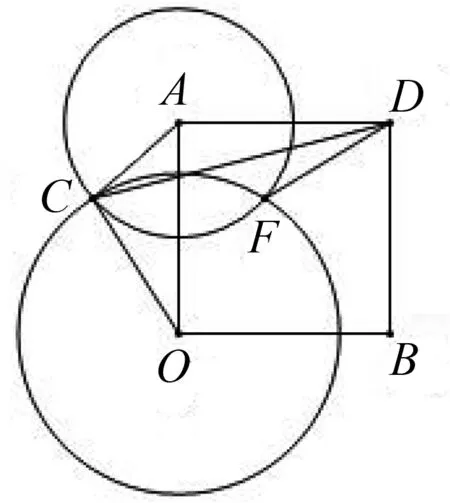
图3
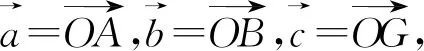
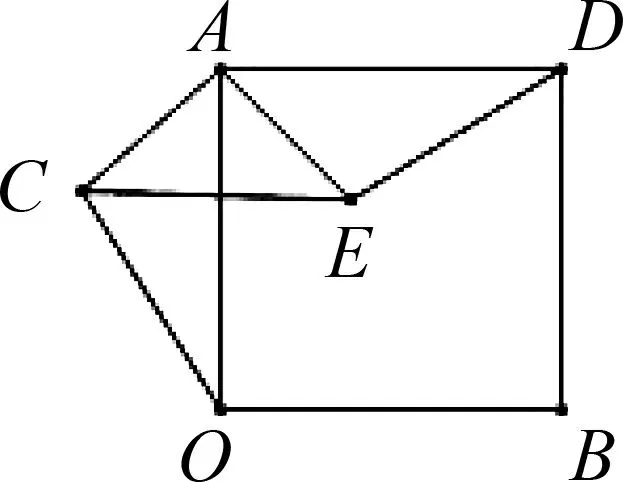
图4
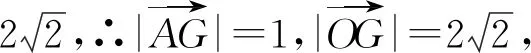
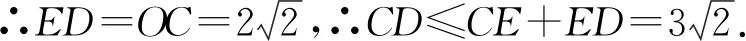
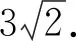
点评:解法3利用形与数的结合,将代数运算转化为几何直观,使得繁琐的计算过程得以简化.
三、拓展
结论的证明可模仿解法3,这里不再赘述.
四、结束语
解题训练是培养学生的数学核心素养的重要手段.多视角解题可以拓宽学生的视野,培训学生的思维能力.向量是沟通几何与代数的桥梁,通过多角度求解向量问题,我们可以更好地体会几何直观与代数运算之间的融合,感悟数学知识之间的关联,加强对数学整体性的理解.
