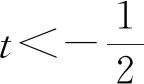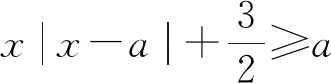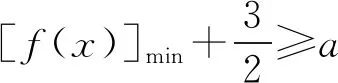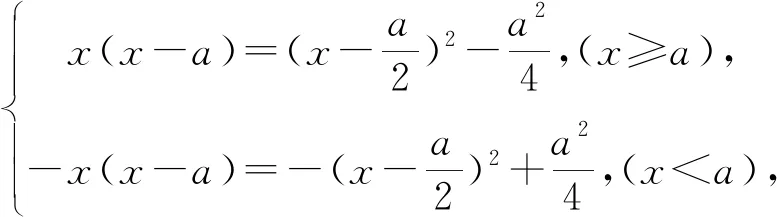例析绝对值不等式问题的四种求解策略
2021-05-18江苏省南京市漂水区第三高级中学211200
江苏省南京市漂水区第三高级中学 (211200) 赵 婷
含有绝对值的不等式问题的求解策略总的来说有两种:即化掉绝对值符号和利用绝对值的性质变形化简,而对于各种典型的题目来说,根据不同的特点又有如下四种简求策略,下面通过典型例题的分析简述这些方法,希望对读者朋友有所帮助.
一、利用绝对值的性质
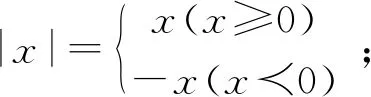
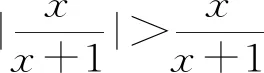
A. {x|x≠-1} B. {x|x>-1}
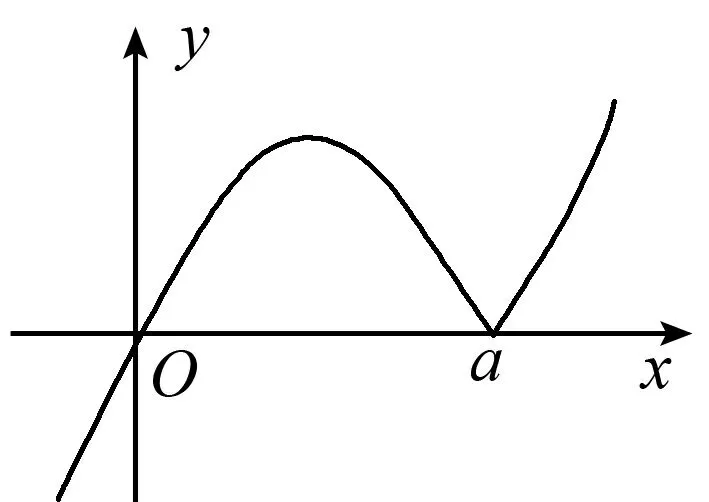
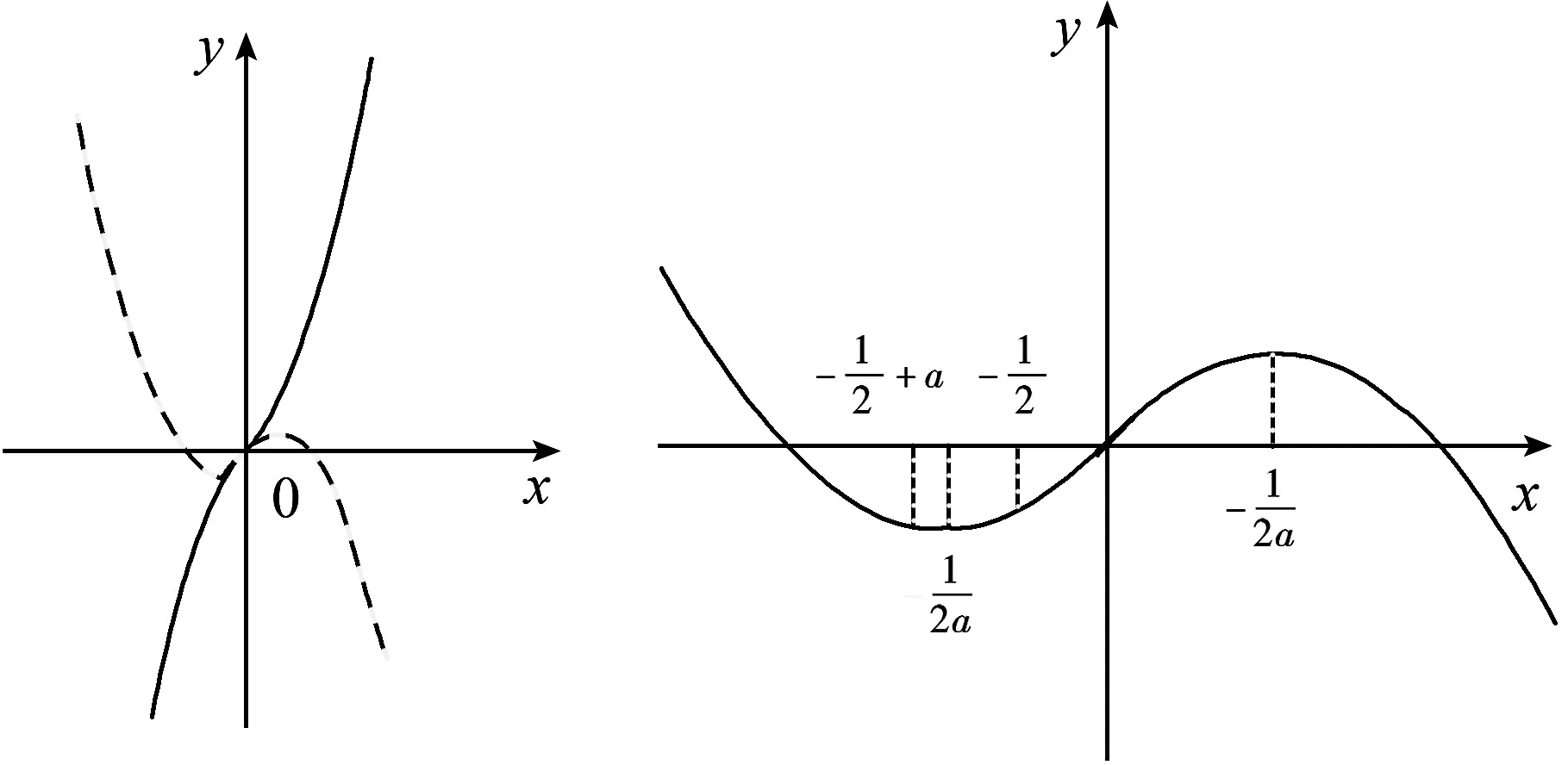
C. {x|x<0且x≠-1} D. {x|-1 评注:根据绝对值不等式的性质直接解不等式,抓住了问题的实质,活用绝对值的性质解题,轻松自如. 例2 若存在x<0,使不等式x2<2-|x-t|成立,求实数t的取值范围. 评注:通过反解不等式,使待求的参数t分离出来,然后构造函数,利用不等式的值域解决了不等式有解问题,这是求解不等式中参数范围的常用方法,而用解不等式的方法化解绝对值问题是解此类题的特色. 例3 求不等式|x-2|-|2x+1|>1的解集. 解析:原不等式为|x-2|>1+|2x+1|,由于此不等式两边都是非负数,将其两边平方得x2-4x+4>1+2|2x+1|+4x2+4x+1,即2|2x+1|<2-8x-3x2,故3x2+8x-24x+2<2-8x-3x2,解得-2 评注:如果能确定不等式的两边都是非负数,可直接进行两边平方运算,如果一边是非负数,另一边不确定也可以通过分类讨论后,再对适合的部分进行两边平方运用,从而达到解题目的. 例4 已知a>0且a≠1,若0 |loga(1-x)|>|loga(1+x)|. 评注:此题的解法比较多,可以分别从去掉绝对值符导、对底数a分类处理等方面考虑,但采用两边同时平方的方法可以同时解决这两个问题,所以是一个比较优化的方法. 对于|x-a|±|x-b|类型的题目即可,由数轴上点x的位置来讨论得出值域;也可用分类讨论化为分段函数,通过画图象可知其值域.而其它形式绝对值范围问题也可以转化为特殊函数,再利用函数图像分析求解. 例5 已知a>0,不等式|x-4|+|x-3| 解析:设实数x,3,4在数轴上对应点分别为P,A,B,则有函数y=|x-4|+|x-3| =|PA|+|PB|,当P在A、B之间时有|PA|+|PB|=1,当P在A、B之外时,有|PA|+|PB|>1,故有y≥1,故按题意只须a>1,即a的范围是(1,+∞). 评注:抓住题目中两个绝对值中自变量x的系数相同这一特点,可以得到的一个简单解法,如果系数不同,就只能通过分类讨论将函数式中的绝对值化去,再利用分段函数的图像分析帮助解决最值问题. 图1 图2 评注:经过对题目整体考察,研究其函数的特点,即过原点、是奇函数等,再利用其函数图象,建立不等式组解决了参数a范围问题.如果试图通过直接解这个含有绝对值的不等式是相当困难的. 绝对值不等式解题的一个重要思路就是化去绝对值符号,将其转变为普通的不等式,而分段讨论是化去绝对值符号的最常用的手段. 例7 解关于x的不等式|loga(ax2)|<|logax|+2,其中a>1. 评注:分段讨论是解决多个绝对值和一些比较复杂的绝对值不等式的基本方法,这里要注意分段点的确定和最后解题结论的整体表述. 图3 解析:设f(x)=x|x-a|,要使不等式恒成立,即使 评注:本题是不等式恒成立问题,通过分析知道问题的核心是绝对值函数的最小值问题,由于函数式中有参数,分类讨论是化解本题难点的重要途径. 绝对值不等式问题是不等式与绝对值交汇的问题,这是高中阶段常见的题型,一般都是考虑先解决绝对值的问题,然后转化为普通不等式或不等式组的问题,由于题目的条件与结论不同,可能出现多种情况,但总体的解题方针和解题方向是一致的.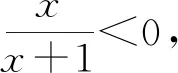
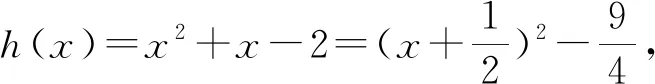
二、两边同时平方
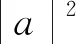
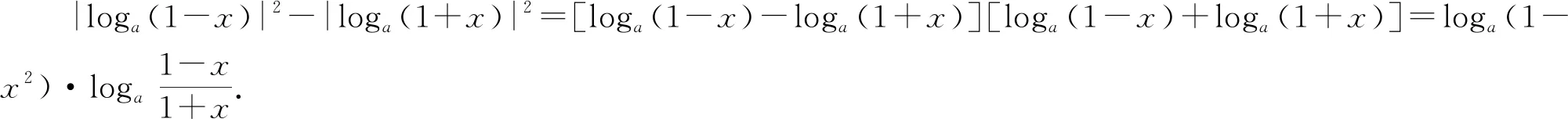
三、以形助数
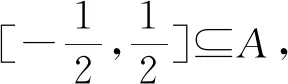
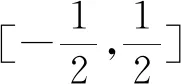
四、分类讨论