轴流压气机一维特性计算方法简介及展望
2021-05-18季路成
王 进, 周 玲,*, 季路成
1.北京理工大学 宇航学院, 北京 100081; 2.清华大学 航空发动机研究院, 北京 100083
0 引 言
计算流体动力学技术的进步以及计算机存储和处理能力的增强,为压气机的设计理念带来了一场深刻的变革[1]。轴流压气机的气动设计体系,已经从最初只考虑简单气体可压缩性方程的一维设计,发展到考虑完全径向平衡方程的二维通流设计、两类流面交互迭代的准三维设计乃至全三维定常与非定常的流动分析与优化设计[2]。然而,要开始一台新压气机的设计,首先需要基于实验数据和经验参数进行一维设计[3]。一维设计,也称为初始设计,主要用于确定压气机的流道几何形状、级数和总长度、轴向负荷分配等[4]。这是压气机设计体系的基础,如果在这一阶段犯了原则性的错误,比如压气机级数给得太少或者压气机长度太短,则在设计后期对压气机做任何改变都不能纠正这种错误,并且会造成严重的后果[5]。一维设计尚未产生详细的叶片几何,在下一步设计之前,需要一种简单、快速、可靠的工具来对大量的一维设设计方案进行评估和筛选,以寻找最有潜力的、可进一步进行详细通流设计的方案,即要对压气机进行一维特性预估。一维特性计算是对轴流压气机进行性能预测的方法之一,相对于二维通流计算和全三维的N-S方程求解,该方法较为简洁,耗时也最短。使用一维特性计算,结合优化算法,可以快速评估改变几何参数、级间引气或放气、间冷等对压气机性能的影响,以及压气机同发动机其他部件的协调[6]。但一维特性计算的缺点也显而易见,即对经验依赖性强。显然,并不能期望仅凭借一维计算就能对压气机的性能作出良好预测。但是,在压气机的全生命设计周期中,不同的性能分析方法适用于不同的设计阶段,而一维特性计算能够在压气机的初始设计阶段发挥重要作用。
本文回顾了轴流压气机一维特性计算方法的起源,论述了其发展趋势与研究现状,对一维特性计算中使用的两种重要方法(级叠加法与平均线法)的基本原理及其所使用的经验模型进行了总结,探讨了两种计算方法的适用范围,为利用实验对一维模型进行改进提供了思路与指引,对一维特性计算进一步发展的趋势进行了展望。
1 一维计算的起源、发展与现状
1.1 起源回顾
20世纪50年代,NASA-SP-36中提出了两种多级轴流压气机非设计性能估算方法——基元叶栅方法和级叠加方法[7]。基元叶栅方法考虑压气机通道内的连续性方程和径向平衡方程,对基元叶栅数据沿径向积分以求解叶片排的性能,并将前一排计算所得的出口条件作为后一排的进口条件,直至得到全部压气机性能。由于对绕叶片流动损失认识的不足、实验数据的缺乏以及计算资源的限制,它在当时并未获得有效的应用。但Howell等给出了一种简化的计算方法,称之为“平均线方法”[8],即只考虑某一个半径处的基元,按压气机的平均半径来估算叶片排的性能。与平均线方法思路不同,级叠加方法直接利用已知的单级性能关系,沿轴向逐级叠加计算,就可以获得整台压气机的性能。Finger等使用级叠加方法定性地表示了高压比压气机在全工况下各级的工作情况,以及单级的性能对整台压气机非设计性能的影响[9]。Medeiros等使用级叠加方法研究了改变静叶安装角对某十六级压气机性能的影响[10]。Geye、Standahar等在某八级高压压气机的气动设计与性能分析中,也采用了级叠加方法[11-12]。不管是平均线方法,还是级叠加方法,都可以称之为一维的特性计算方法。对于平均线方法,“一维”体现在计算是沿某一个半径进行的,有别于沿多个半径进行的计算(二维通流计算);对于级叠加方法,“一维”体现在计算是建立在级的平均性能的基础上,因此,计算也仅仅只有一个维度。
1.2 发展趋势与研究现状
随着一些学者和机构对压气机设计研究的深入,特别是美国国家航空航天局(National Aeronautics and Space Administration,NASA)公开了他们在压气机设计研制方面大量而细致的工作,极大地丰富了人们对压气机内部流动机理和损失机制的认识。与此同时,计算机也获得了飞速的发展。通流方法已经能够被应用于压气机的特性计算之中[13]。似乎随着计算资源的丰富,一维计算已经显得不合时宜,在此期间对其研究的学者也大为减少,已难以见到相关的公开文献发表。但是在70年代末,为了获得压气机在非设计工况下的性能,特别是临近失速和堵塞工况时,通流方法难以被有效地应用,Howell和Calvert宣称英国国家燃气轮机研究院(National Gas Turbine Establishment,NGTE)又重新拾起了一维方法,并且取得了一定的成功[14]。他们开发了一种新的级叠加方法,对四种级数从2到8不等、总压比在2到10之间变化、子午流路形状不同的压气机/风扇的性能作出了很好的预测。在此同期或稍前,俄罗斯的一维特性计算HARIKA程序也正式形成。
Howell的成功重新唤起了研究人员对一维特性计算的热情。NASA的Lewis研究中心紧随其后,利用从实验数据中总结的级性能关系,使用级叠加法对一个两级低压比风扇的性能作出了良好预测,并公开了程序代码[15]。之后NASA公开的技术报告再一次对级叠加法的本质及其适用条件进行了总结,并欲将该方法拓展到离心压气机领域[16]。Jack等试图基于两种现有的分级叠加性能计算模型——NASA的STEINKE模型和NGTE的H-C模型的组合,来提高多级轴流压气机非设计性能预测的精度[17]。但Geye等指出,只有用某一台多级压气机中得到的级性能关系来估算具有相似级的、总压比方面相差不太大的压气机的性能时,才可能得出良好的结果[11]。
随着计算流体动力学的蓬勃发展,叶栅性能数据的获取已然轻而易举,并且已经有大量基于实验数据的叶栅性能关联式得以公开,许多学者转而使用平均线方法进行一维特性计算。Dahlquist在一维平均线计算中对压气机内的损失来源以及用到的经验关联式进行了比较和总结[18]。Smith在平均线模型中引入了角动量守恒方程,使静子入口截面的参数计算更为准确[19]。Madadi、Asli、Kidikian等使用平均线方法计算了NASA典型压气机级的性能,进一步证实了平均线方法的有效性[20-23]。Miller基于简单径向平衡假设计算了展向多个基元叶片的性能,提高了平均线分析方法的精度[24]。为得到压气机的失速边界,White等在平均线分析中引入了喘振预测模型,并给出了堵塞因子的计算方法[25]。平均线分析作为一种压气机性能计算方法,自然也能应用于压气机的优化设计,并且具有简单快速的特点。Johnson利用平均线方法研究了可变几何对压气机性能的影响[26]。Asli等应用平均线分析对一些无量纲设计参数(如流量系数和反力度等)对压气机喘振裕度的影响进行了研究[27]。Rozendaal开发了简化多级轴流压气机气动设计的程序,该程序允许平均线分析和通流分析进行设计迭代,极大缩短了压气机初始设计阶段的设计周期[28]。
国内对一维特性计算的研究较少,且多数学者的研究限于对俄罗斯一维特性计算HARIKA程序的简单改型与应用上,并未深入其算法原理与理论模型。李志刚等阐明了利用HARIKA程序计算压气机特性的步骤与流程,并利用该算法研究了变导叶安装角对压气机特性的影响[29]。李立君、斯夏依等对HARIKA程序进行了改进[30-31]。丁伟利用平均线方法优化了某六级高压压气机的轴向参数分布[32]。Cai等在NASA的模型中引入了失速判据,成功预测了某台三级轴流压气机的喘振线[33]。崔凝等使用逐级叠加法建立了变几何多级轴流压气机全工况性能预测模型[34]。陈江等在某五级低压轴流压气机的气动设计中,使用HARIKA程序进行了初步设计与性能分析,证实了HARIKA程序的工程实用性[35]。黄雄武等初步探讨了利用HARIKA程序计算高效率高负荷压气机级时经验修正系数的取值范围[36]。钟勇健等在HARIKA程序中加入了级间引气模型,研究了E3压气机在不同引气方案下流道形状和性能的变化规律[37]。史磊、张军等结合遗传算法利用HARIKA程序对压气机进行了一维优化设计[38-39]。夏凯利用三维数值计算获得的级性能关系研究了某低压九级轴流压气机的喘振特性[40]。
2 级叠加方法
级叠加方法直接使用单级性能关系获得整机的性能,在计算资源匮乏的年代,该方法成为计算轴流压气机非设计性能的不二选择。20世纪50年代初,NASA已经对该方法应用得非常纯熟。因其形式较为简洁,本文首先对级叠加方法展开介绍。
2.1 简介
级叠加法利用级性能关系,从入口条件开始,对压气机进行逐级叠加计算,以获得压气机出口的参数。所谓的级性能关系,可以是负荷系数与流量系数、绝热效率与流量系数之间的关系,如图1所示。当压气机进口条件已知时,从第一级的性能关系就可以获得第一级的负荷和效率,从而计算出第一级的压力比和温度比。第一级的计算结果提供了第二级的进口条件,对整台压气机连续地进行逐级计算,就可以计算出总的压比和效率。但级性能关系先前一般无法得知,并且其通用性往往较差,即使有了此类的关系,也只能将其应用于预测同类的具有相似几何结构的压气机;而且不同文献中使用的这类关系也不尽相同,但其本质都是利用一些经验模型来评估压气机级在设计工况下所能达到的效率和负荷以及在偏离设计工况下效率和负荷的变化。
2.2 级性能关系
2.1节已经指出,不同的学者用以预测的级性能关系往往形式各异,下面给出一些经典文献中较为成功的预测案例所使用的性能关系以供参考。首先介绍NASA的STEINKE模型[15],该模型使用的经验关系与图1类似。由图1可见,级的性能在相当宽广的马赫数范围内具有良好的通用性;但当马赫数过高时,对于不同的转速,为正确表示级的性能,可能需要一簇曲线来描述,如图2所示。
图2即为Steinke使用的级性能图,该图展示了在偏离设计转速下负荷系数随流量系数的变化。显然,相对于单一的性能曲线,该图能够更为准确地模拟真实的流动环境。
Howell和Calvert使用的性能关系如图3所示(H-C模型)[14],与NASA的STEINKE模型有所不同,该图给出的是NGTE的C135压气机第一级在偏离最大效率点时级的相对温升、相对效率与相对流量的关系。
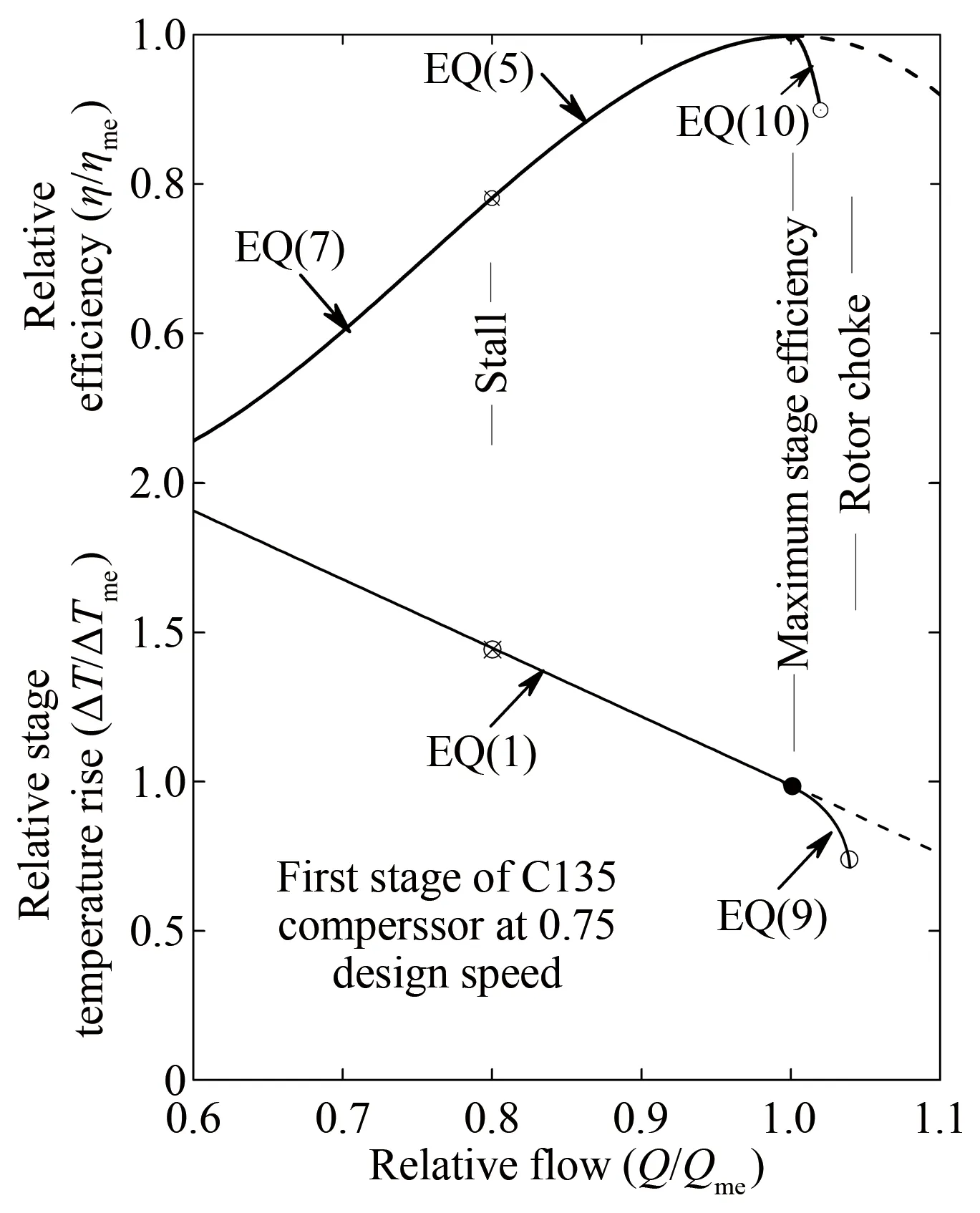
图3 C135压气机首级的性能[14]Fig.3 First stage performance of C135 compressor[14]
为判别不同运行工况下的关键状态,如失速、堵塞以及最佳状态,可进一步利用的经验关系如图4所示。该图给出了设计转速下转子的失速攻角、堵塞攻角以及最佳攻角随进口马赫数的变化关系。
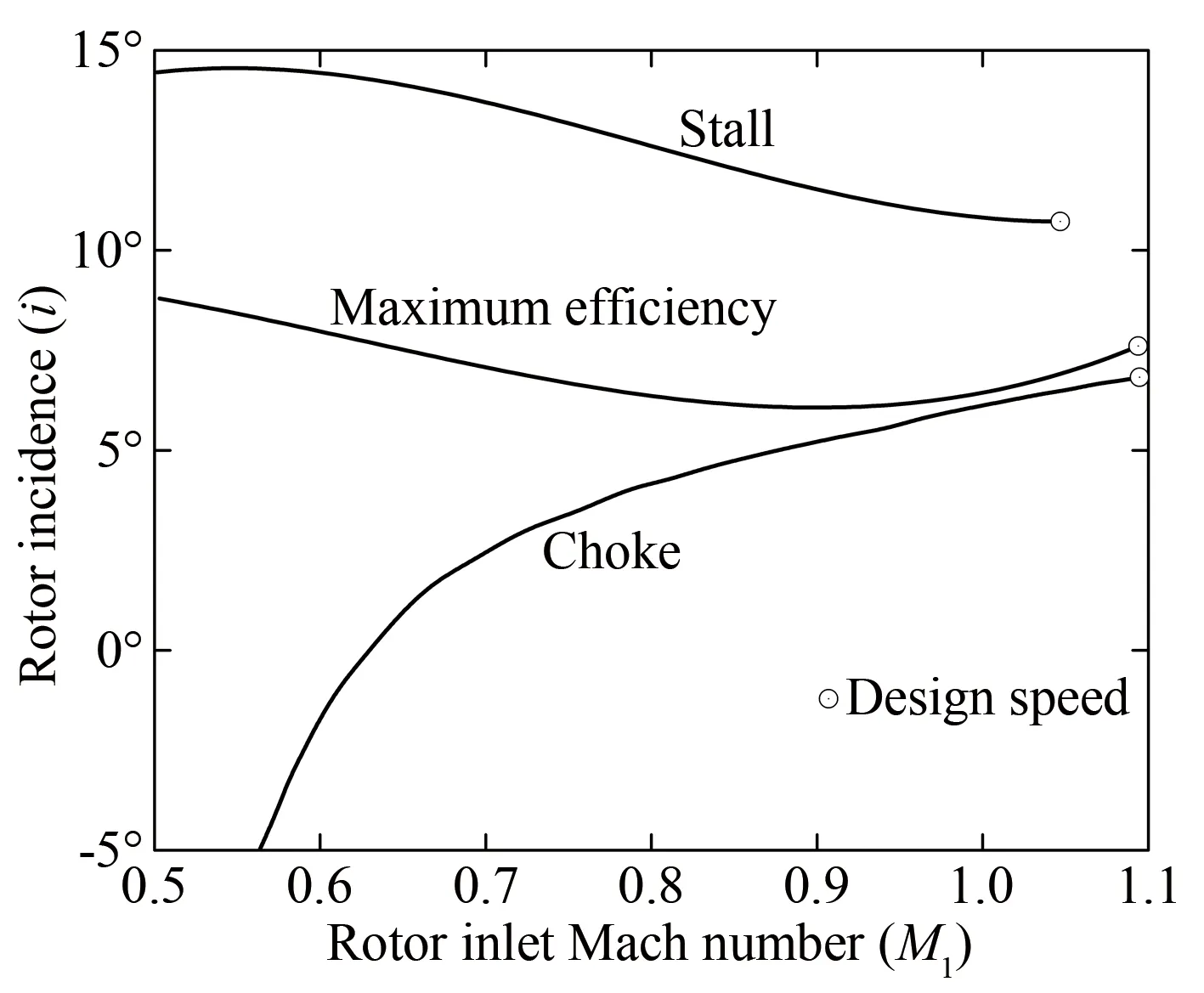
图4 C135压气机首级转子平均半径处的马赫数与最佳攻角、失速攻角以及堵塞攻角的关系[14]Fig.4 Maximum efficiency, stall and choke incidences and rotor inlet Mach numbers at mean radius for first stage of C135 compressor[14]
2.3 HARIKA程序
用级叠加方法预测轴流压气机的性能依赖于从实验数据中总结的级性能关系,公开文献中给出的级性能关系种类繁多,并且多是从一台压气机中得到的,缺乏代表性。而俄罗斯的HARIKA程序中的经验关系是建立在对大量的实验数据进行统计分析的基础上,其体系宏大,模型众多,具有较高的参考价值。从某种意义上讲,HARIKA程序仍然是不可多得的一维性能分析工具,是无法以国内的设计经验和实验资源所能够完成的设计软件。图5给出了HARIKA程序的计算框架,本小节将对HARIKA程序的算法逻辑及其改进途径进行简要分析。
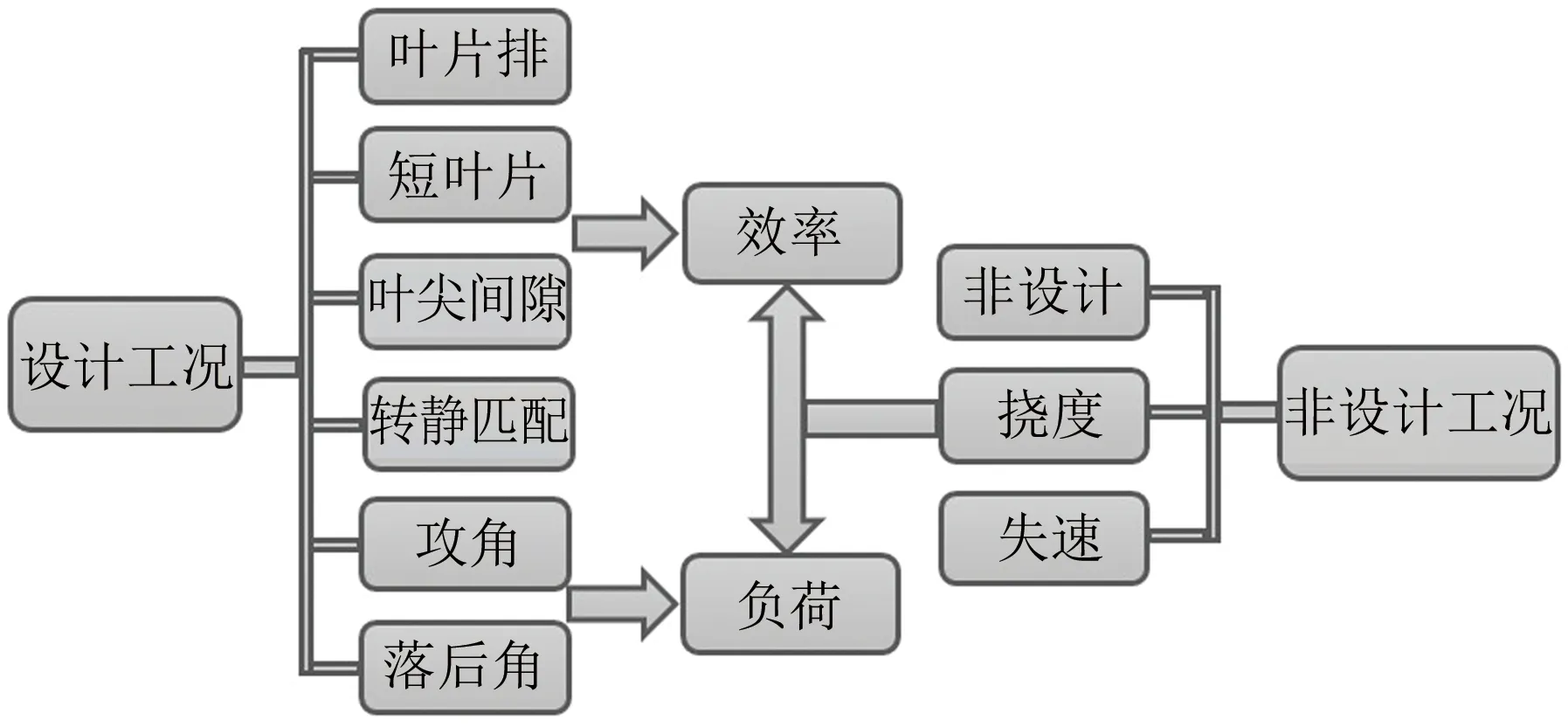
图5 HARIKA程序计算框架Fig.5 Calculation framework of HARIKA program
HARIKA程序在计算每一个级时,都会先估算在设计工况下该级所能达到的效率和负荷,效率计算以单独叶片排的效率为基准,在此基础上再考虑展高、叶尖间隙、转子叶排和静子叶排的匹配对级效率的影响,使用经验公式对级效率进行修正。负荷计算是通过攻角和落后角模型确定气流通过叶栅的折转,利用轮缘功公式进行计算。在非设计工况下,需要对效率和负荷进行修正,并在最大挠度位置变化或发生失速时对效率和负荷进行附加修正。
HARIKA程序形成较早,彼时压气机还处于较低的负荷水平,将其用于预测高效率高负荷压气机时难免有一定的局限性。因此,需要开展先进压气机级的相关实验,对程序中的效率模型和负荷模型进行修正,以提高预测精度,从而发挥其应有的工程应用价值。
2.4 对级叠加方法的评述
级叠加方法作为一种压气机非设计性能分析工具,在早期压气机设计中获得了广泛的应用。图6给出了Cai等使用级叠加方法预测的某三级压气机的特性[33],可以看到,预测结果与实验结果具有良好的一致性,在效率线上有少部分点偏差较大,可能是由于级叠加方法无法考虑级间的相互作用。需要指出的是,这种方法成功与否,取决于用以计算总性能的单级性能关系的准确程度。这也正是级叠加方法所面临的困难,一般而言,级性能关系并不容易获得。但在对压气机进行改型设计时,如果用原型的级性能关系估算改型的压气机性能,还是能够得到比较好的结果。
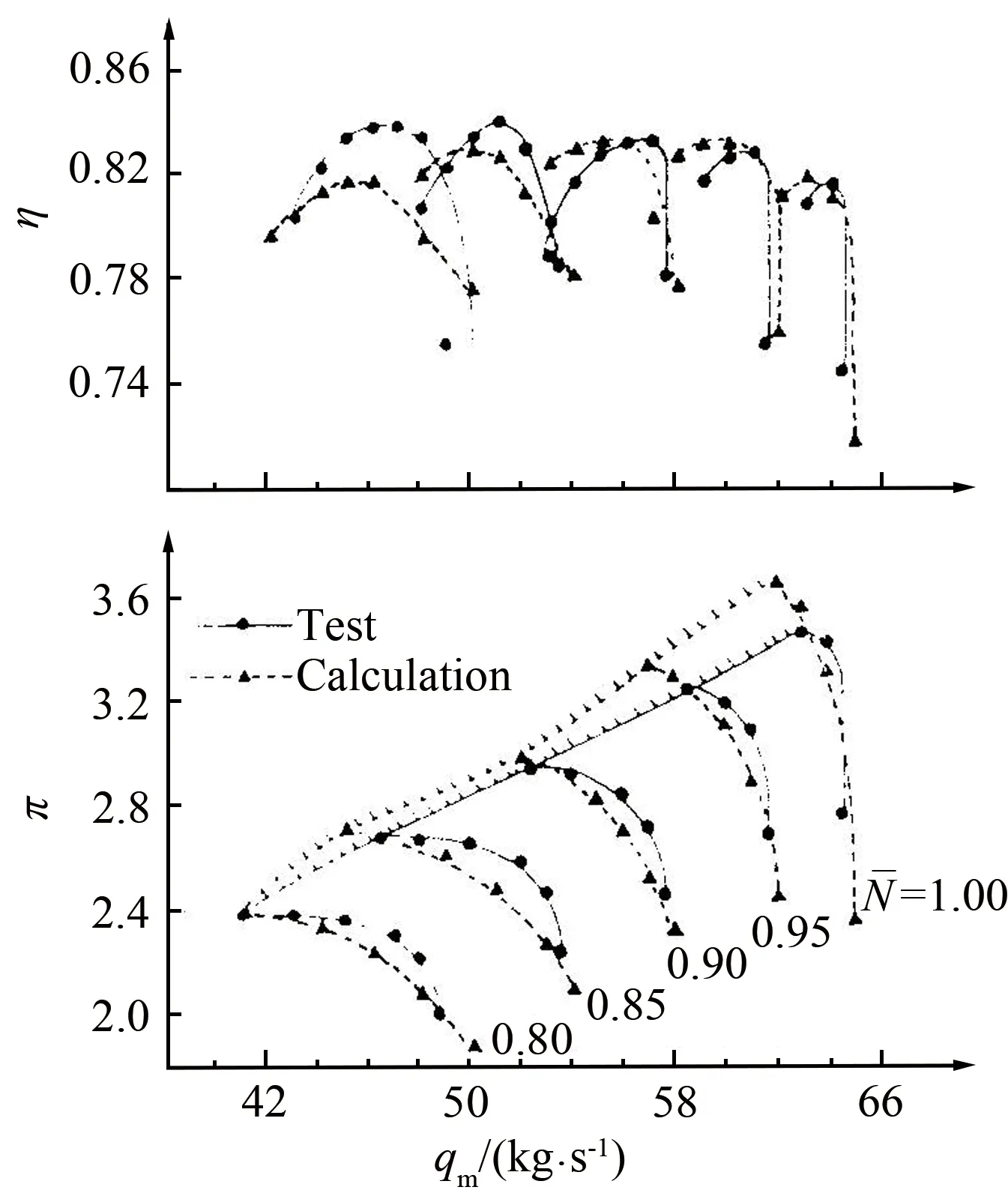
图6 某三级压气机特性[33]Fig.6 A 3-stage compressor characteristic[33]
3 平均线方法
从国外的研究趋势来看,随着基元叶栅性能数据的丰富以及对压气机损失机制认识的深入,大量的经验关联式得以总结公开,因此更多的学者选择使用平均线方法来进行压气机的一维性能分析。下面介绍平均线方法。
3.1 复杂流动的简化
如图7(a)所示,一维平均线模型中假设流动是一维定常绝热无黏的,气流在径向和周向的变化被忽略,某一半径上基元叶栅的性能被认为能够代表整个叶片排的平均性能[41]。气流通过叶栅的折转、黏性效应造成的损失均可以通过经验模型进行计算。这样就可以将复杂的三维流动简化为一维流动,在平均线上逐叶片排计算压力和温度等流场参数。实际上,这种计算更多的是一种热力计算而非流动分析[4]。然而无论对流动作何种程度的近似与假设,流体的运动始终遵循的仍然是三大守恒方程,一维平均线模型也不例外。对一维平均线计算,其本质是利用损失和落后角经验关联式,依托速度三角形(如图7(b)所示),在平均半径上联合流量方程、动量方程、能量方程,以及理想气体状态方程、热力学第二定律等来求解压气机各个截面的平均气流参数。
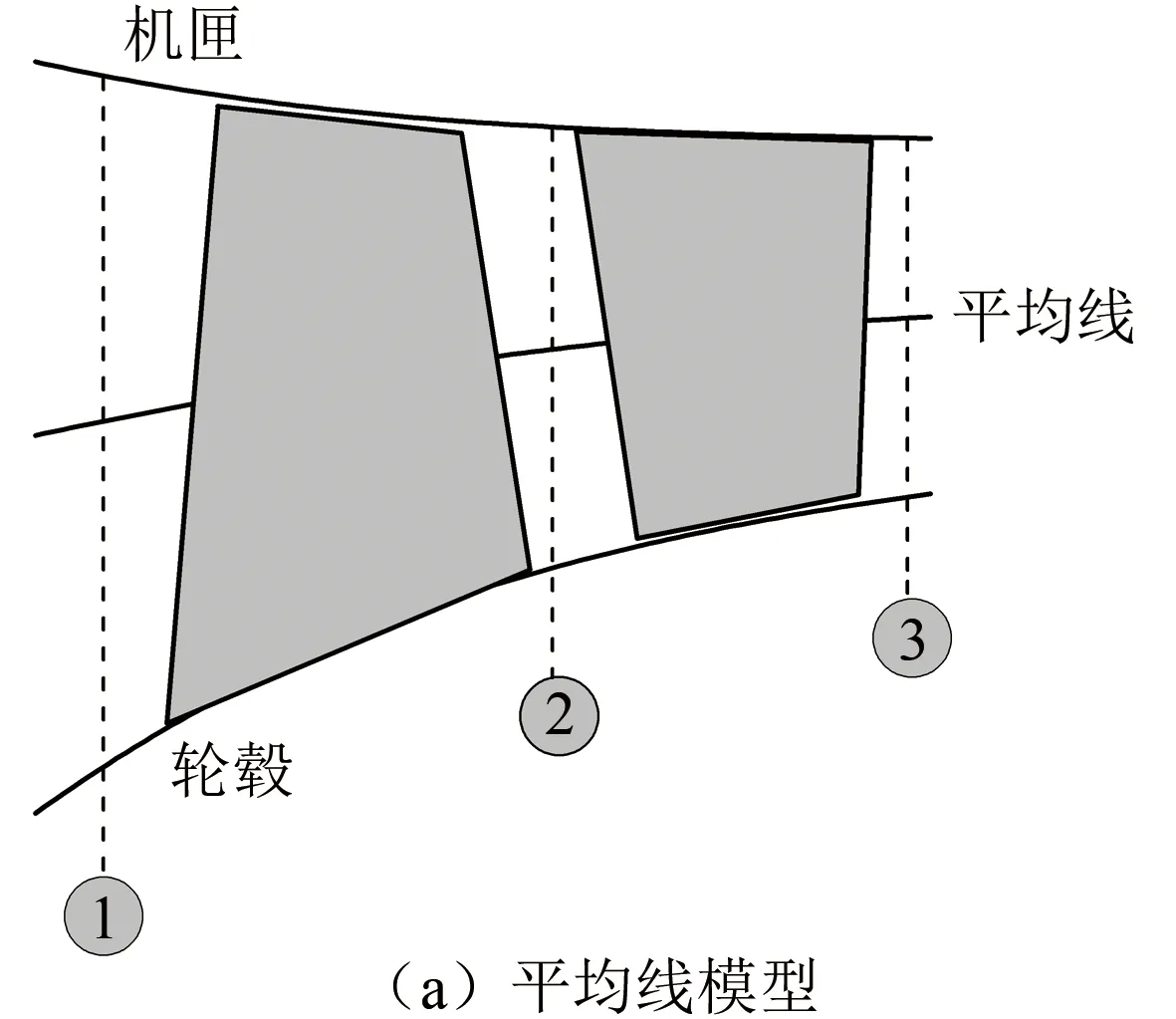
图7 平均线方法Fig.7 Meanline method
在平均线模型中,为获取气流通过叶栅的折转以及黏性效应引起的损失,攻角/落后角模型以及损失模型的应用显得尤为重要,下面就对这两类模型进行详细介绍。
3.2 攻角/落后角模型
为预测气流通过叶栅的折转,从而确定基元的负荷,必须给出可靠的攻角/落后角关联式。特别是设计攻角/落后角关联式所确定的设计点参数,将作为非设计点性能计算的重要参照,其精度是影响特性计算成功与否的重要因素。设计攻角/落后角有多种形式,不同的研究机构和学者使用的关联式的细节略有不同,这在很大程度上依赖于他们的设计经验,但这些关联式本质上是一样的。下面介绍几种经典的攻角/落后角模型。
3.2.1 设计攻角
NASA-SP-36中给出的关系式最为人所熟知[7]:
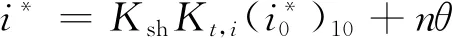
(1)
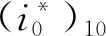
Wright和Miller的关联式则代表了英国罗罗公司的研究思路[42]:
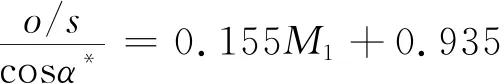
(2)
式中,o/s为喉部宽度与栅距之比,α*为设计进口气流角,M1为进口马赫数。
Miller和Wasdell给出了如下关系[43]:
i*=X+Yσ-Zθ
(3)
式中,X,Y,Z为安装角的函数,σ为稠度。
上面的关联式是依据二维平面叶栅性能数据总结得到的,显然与真实压气机内的流动还有一定的差距。为了考虑三维效应,Davis对设计攻角进行了如下修正[44]:
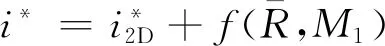
(4)
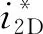
3.2.2 设计落后角
同样,NASA-SP-36中的落后角模型也获得了极为广泛的应用[7]:
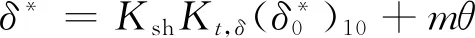
(5)
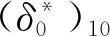
卡特提出的落后角公式得到了业界广泛的认可,许多学者对卡特的落后角公式进行了修正和改进。卡特基本落后角关系式如下[46]:
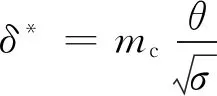
(6)
式中,mc为安装角的函数。
如果进口马赫数超过了临界马赫数,Roland等建议对设计落后角进行如下修正[47]:
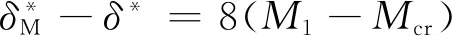
(7)
3.2.3 非设计落后角
为进行非设计工况下的计算,还必须给出偏离设计工况时的落后角模型。一般叶栅进口攻角的变化会影响非设计工况下的落后角,因此非设计落后角可以表示为:
δ-δ*=f(i-i*)
(8)
Creveling、Miller等利用实验数据拟合出了类似的关系[13,43]。
叶栅进出口轴向速度的变化也会对非设计落后角产生影响。为了考虑该因素,Aungier使用的非设计落后角关系式如下[48]:
δ=δ*+(∂δ/∂i)*(i-i*)+10(1-Ca2/Ca1)
(9)
式中,Ca2/Ca1为轴向速度比。
Swan则将非设计落后角与进口马赫数和当量扩散因子Deq相关联[49]:
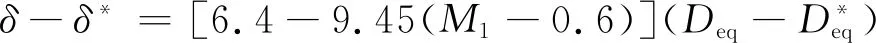
(10)
3.3 损失模型
预测压气机的性能,除提供气流折转的信息,还需要给出由于黏性造成的损失。但是压气机内有关损失的分类并不是很严格,不同时期不同学者使用的损失模型的组合也不尽相同。实际上,也很难将某一项损失从复杂的流动中单独分离出来。最常见的损失是叶型损失、激波损失和端区损失[50]。在全亚声速流动中,激波损失并不会产生。有时候,端区损失可以进一步分为叶尖泄漏损失、环壁附面层损失以及二次流损失。在一维平均线模型中,一般考虑叶型损失、激波损失、端区损失以及叶尖泄漏损失。下面对这些损失源项逐一论述。
3.3.1 叶型损失
叶型损失主要是由叶片吸力面和压力面上产生的附面层引起的,附面层在叶片后缘交汇形成尾迹,引起总压损失,如图8所示。
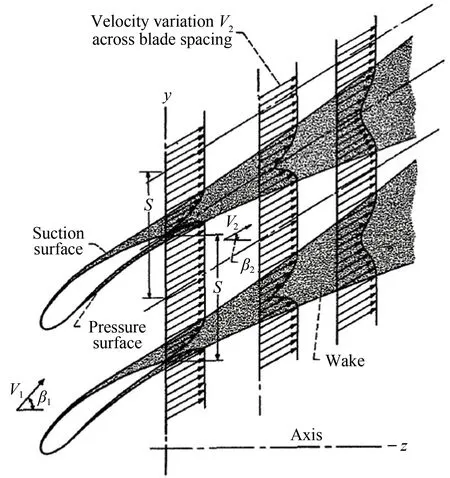
图8 叶片表面附面层和尾迹的发展[51]Fig.8 Development of surface boundary layers and wake in flow about cascade blade sections[51]
Lieblein等从大量的二维低速平面叶栅实验中总结出了任意流动工况下基元负荷与损失之间的关系[51]:
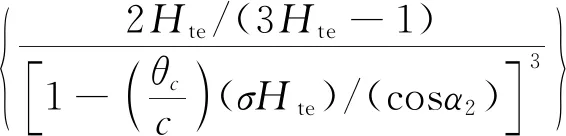
(11)
式中,θc为尾迹动量厚度,c为弦长,Hte为尾缘的形状因子,α为气流角,下标1、2分别表示进口和出口。
事实上,式(11)中大括号里面的项通常不太重要,并且在设计工况下,尾迹动量厚度可以与当量扩散因子Deq很好地关联。因此,若用当量扩散因子表示损失,且忽略与Hte有关的项,并用速度W替换气流角项,则[48]:
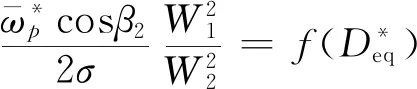
(12)
式(12)中关于叶型损失的表示更方便计算。Lieblein的关联式是根据二维低速叶栅得到的,Koch和Smith应用可压缩边界层理论,将Lieblein的损失关联式扩展到了高马赫数和高雷诺数范围,并且考虑了流道收缩以及叶片粗糙度的影响[52],给出了无量纲尾迹动量厚度θc/c、尾缘形状因子Hte和气流扩散度Wmax/W2、进口马赫数M1、雷诺数Re以及流道收缩率h1/h2之间的关系:
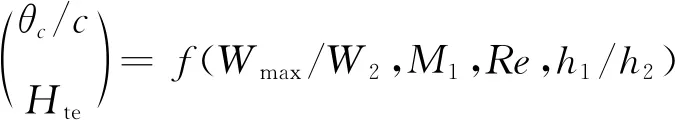
(13)
利用式(13)计算出动量厚度和形状因子后代入式(11),便可以计算出设计点的叶型损失系数。Koch和Smith的叶型损失关联式考虑了诸多因素的影响,其可信度较高。
Jansen和Moffatt指出,当叶栅通道中局部马赫数达到1时,损失会额外增加,此时叶栅进口的马赫数称为临界马赫数。当叶栅进口马赫数超过临界马赫数时,需要对叶型损失进行修正,具体表达式为[53]:
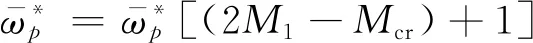
(14)
3.3.2 激波损失
激波是跨声速流动中的重要现象,气流经过激波会造成总压损失。如图9所示,Miller等的激波损失模型得到了广泛的应用[54]:假设气流在叶背前缘发生普朗特-麦耶尔膨胀,经过叶栅通道入口处的正激波后造成总压损失,这样就可以利用简单的正激波关系计算激波损失系数:
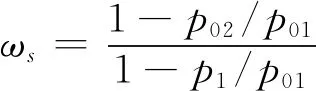
(15)
式中,p为压力,下标0表示滞止条件。Miller等的激波损失模型代表了跨声速基元流动中的一种典型工况,对于从公开文献中获得的实验数据,这种方法确实能产生效率随马赫数的正确变化[42]。
Koch和Smith则直接给出了激波引起的熵增关系[52]:
[1.28(M1-1)+0.96(M1-1)2]}
(16)
式中,tLE/s为相对于栅距的叶型前缘厚度,R为气体常数。显然,该经验公式考虑更多的是叶型前缘的钝体效应所引起的激波损失,因为公式中包含了叶型厚度项。
3.3.3 叶尖泄漏损失
图10显示了叶片上端壁处复杂的涡系结构,通道涡和泄漏涡会造成旋涡耗散损失,因此在特性计算中应予以考虑。Storer等的研究表明叶尖泄漏损失是由吸力面和压力面的压差驱动的射流与主流进行掺混造成的[55],并给出了计算叶尖泄漏损失的近似公式[56]:
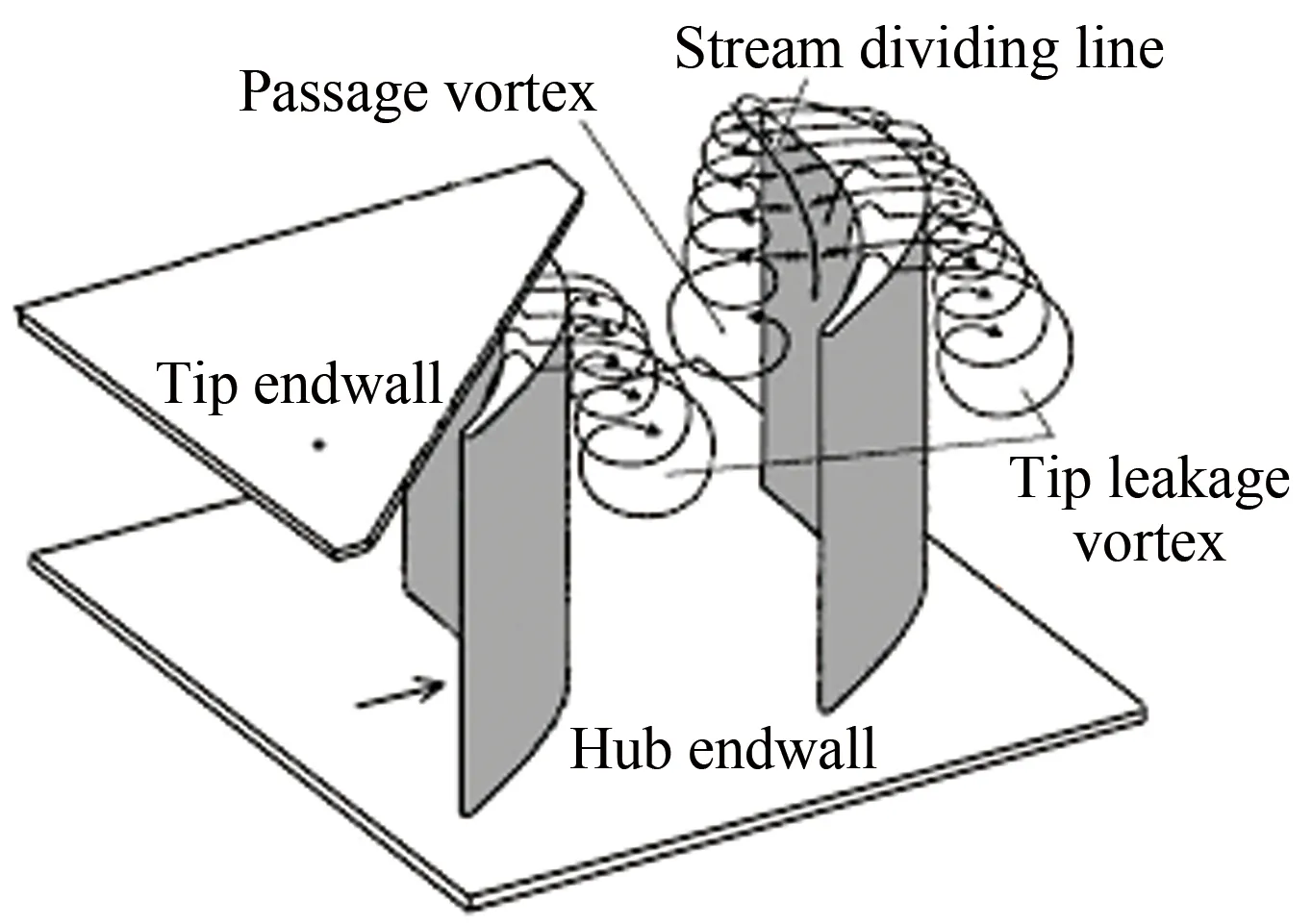
图10 上端壁处的叶尖泄露涡和通道涡Fig.10 Tip leakage vortex and passage vortex at tip endwall
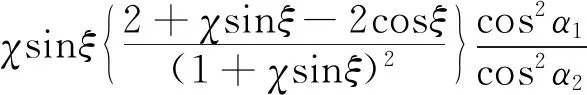
(17)
式中,χ是叶尖泄漏面积与主流面积之比,ξ的物理意义是泄漏流的方向。Storer和Cumpsty认为上式对叶尖泄漏流的估计可能过于严重,因此建议对χ乘以一个修正系数。实际上,对于设计良好的叶片,由上式计算出的总压损失可能仅为入口动压头的1%,因此在平均线计算中叶尖泄漏损失并不在压气机的主要损失来源中占有地位。
Aungier等指出,由泄漏流引起的压力损失与泄漏流量和主流流量之比成正比[48]:
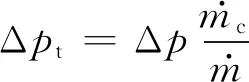
(18)
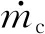
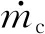
3.3.4 端区损失
端区流动对压气机的性能有非常重要的影响,端区损失也在压气机的总损失中占据了主要地位。自Mellor和Wood导出了轴流压气机中完整的边界层方程[57],在性能分析中引入端区损失模型已经成为了一种普遍的做法[58-59]。但端区流动固有的复杂性使得经验建模的难度很大。因此文献中给出的损失模型实际上都基于非常有限的物理假设,并且多数学者研究的都是直列叶栅中的端区流动现象,这种流动并不能代表压气机内的真实流动,故而这些经验模型的准确性也令人怀疑。
Koch和Smith给出了端区损失引起的级效率的亏损[52]:
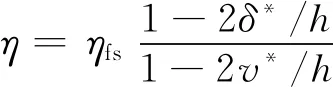
(19)
式中,ηfs为自由流效率,h为展长;δ*为边界层动量厚度,v*为边界层切向力厚度,但这两项在原始文献中是以图表的形式呈现的,从中可以看到切向力厚度的关联性实际上很差,因此Aungier等对该式进行了修正[48]。
Hübner和Fottne认为端区损失是轮毂区和叶尖区二次流损失的平均值[60]:
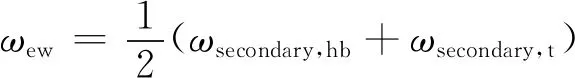
(20)
式中,ωsecondary,hb,ωsecondary,t可以表示为:
ωsecondary,hb/ωsecondary,t=f(β1,β2,h/c,τ/c)
(21)
h/c为展弦比,τ/c为叶尖相对间隙,β为气流角。
Wright和Miller将端区损失与展弦比h/c、叶尖相对间隙τ/c、叶片扩散因子D进行关联[42]:
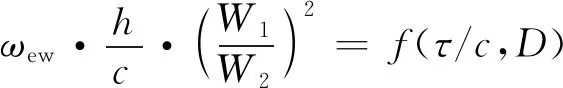
(22)
该关联式类似于常见的叶型损失关联式,将端区损失与叶片气动负荷进行关联,但遗憾的是Wright和Miller并没有给出该式的显式表达。从式(21)和(22)可以看到,端区损失实际上与展弦比、叶尖相对间隙以及叶片负荷有关。
3.3.5 非设计损失
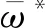
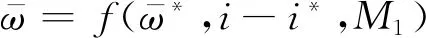
(23)
Miller、Aungier、Jansen等在压气机的性能分析中都使用了类似的表达式[43,48,53]。
另一类方法是先估算出非设计工况下的尾迹动量厚度,然后利用Lieblein的损失关联式进行计算。Swan将尾迹动量厚度与当量扩散因子以及进口马赫数进行了关联[49]:
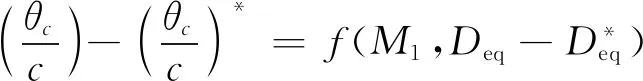
(24)
一般认为使用式(23)给出的关系是一种可靠的做法。
3.4 失速与堵塞
进行特性计算时需要判断级的失速以及堵塞边界,但实际上失速和堵塞现象很难通过经验关系进行判别,有学者直接使用叶栅的稳定工作范围来近似表示失速和堵塞边界。对于失速的判定,Aungier等给出了如下判据[48]:
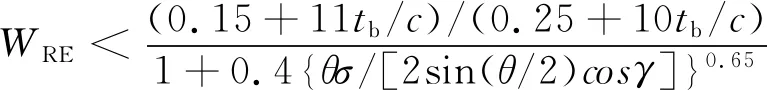
(25)
式中,WRE为等效相对速度比,tb/c为叶型的相对最大厚度,γ为安装角。当满足式(25)时,即可判定为失速。需要说明的是,式(25)是针对中弧线为圆弧的叶型导出的。
Koch提出的失速静压升模型将叶栅通道比拟为二维扩散器,从而给出了单排叶栅所能达到的失速极限压升,并且还考虑了轴向间距、叶顶间隙以及雷诺数的影响[61],应用Koch的模型判别失速能获得较为合理的结果。此外,有学者使用一些简单的参数组合来近似判定失速。如Mckenzie建议采用最大静密度比ρ2/ρ1[62];Howell等则使用ηΔH[14],式中η为等熵效率,ΔH为级的滞止焓增。对于堵塞的判定,公开文献中少有提及。一般当某一个流量点的压比小于给定值时即可停止计算。
此外,由于气体的黏性效应,壁面边界层的发展会引起实际通流面积减小。因此在特性计算中必须对压气机的通流能力予以估计。Howell等假设堵塞因子基于每个壁面的位移厚度是当地半径的0.25%[14],而White等则采用了更为严谨的方法迭代求解轮毂和机匣的边界层位移厚度[25],堵塞因子的计算公式如下:
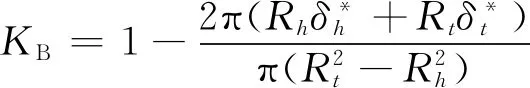
(26)
3.5 对平均线方法的评述
图11给出了White等使用平均线方法对C135两级跨声压气机进行性能预测的结果[25]。由图可见,只要所用的损失和落后角关联式适用于相应的叶型,预测就可以获得与实验相一致的结果。图11还显示了White的平均线方法(Bladestack model)与Calvert的级叠加方法(Calvert model)预测结果的对比。可以看到,White的模型倾向于给出更高的压比,从而在喘振线的预测上表现得更为出色,而Howell的模型更好地捕获了效率变化的趋势。
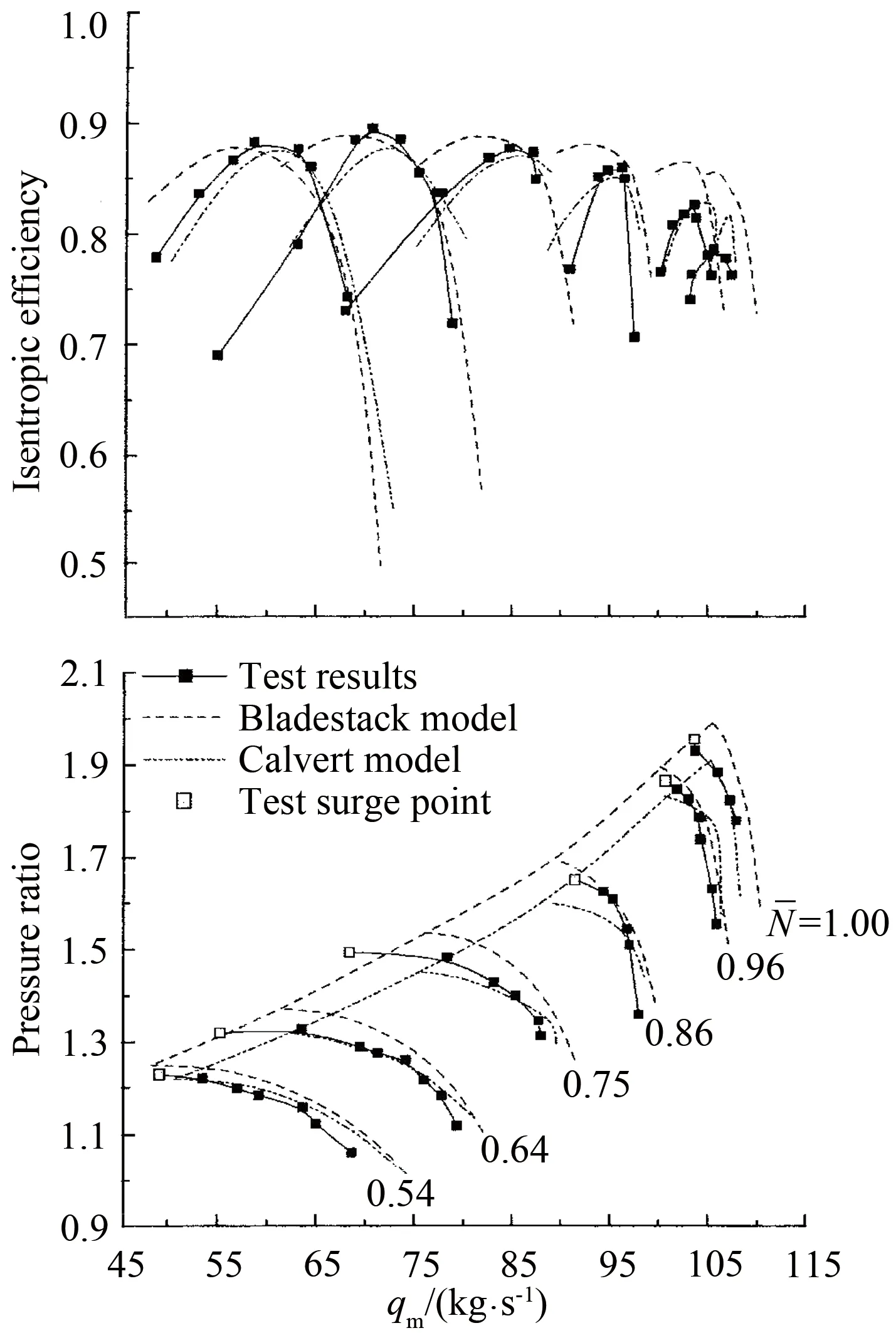
图11 C135两级跨音压气机特性Fig.11 C135 two-stage transonic compressor prediction
实际上,用平均线方法计算压气机性能的困难在于压气机内的流动是三维的,而通常所使用的基元数据是根据二维流动得到的,特别是平均线模型将压气机内的复杂三维流动简化为一维流动,这样得出的计算结果恐怕难以令人信服。在平均线分析中,与熵增有关的损失模型和与表面分离有关的落后角模型往往具有相当强的经验性,其精准与否决定了性能预测的成功与否。而用于预测损失和落后角的经验关联式通常基于传统的NACA叶型或DCA叶型,对于一些先进的压气机叶型(如可控扩散叶型或任意造型),这些经验关联式的精度有限;同时由于压气机内流动的高度复杂性,倾向于控制压气机性能的端区流动,难以被很好地建模,这不仅是一维分析,也是二维通流分析所面临的困难与挑战。
4 总结及展望
虽然计算流体动力学模拟技术已经在压气机设计领域获得了广泛的应用,但压气机的设计过程始终是一个从无到有、从一维到三维的过程。无论三维的流体动力学如何发展,一维设计与分析仍将在压气机设计体系中扮演重要角色。即使这种分析的精度有限,但它确实提供了一种简单、快速、易于收敛的方法,使得研究者能够直接根据实验数据拟合的关联式来模拟压气机内的真实流动,从而定性地说明压气机的工作特性。级叠加方法预测是否有效,取决于所使用的级性能关系的准确程度,一般用从某台压气机中得出的级性能关系去预测具有相似级的压气机时,才可能得出比较好的结果。平均线方法由于严格区分出了压气机内的各项损失来源,因此具有一定的通用性。但在平均线分析中,损失和落后角模型的精度有限,预测的性能与真实的流动相比还有一定的差距。
在一维分析中,由于流动控制方程过于简化,因此计算的准确度将强烈依赖于所使用的经验关联式的质量,这也正是一维计算的精髓所在。现今,数值模拟已经成为压气机设计的重要手段,并且随着航空发动机和燃气轮机研究的深入,相关的实验工作也会逐步开展。如果能从数值模拟的结果或大量的实验数据中总结出可靠的经验模型反馈给一维设计,则将显著提高一维计算的精度,从而缩短压气机设计周期,提高设计质量。进一步地,关于级叠加方法,因我国工程界使用的主要还是俄罗斯的HARIKA程序,则应当用现有的先进压气机级实验数据更新程序中的性能关系,以提高预测精度,从而进一步发挥其应有的工程应用价值。而对平均线方法,需要针对新的叶片造型发展损失和落后角模型,使平均线分析给出更为合理的计算结果。
