通气空泡水洞试验壁面影响理论分析及空化数修正

陈伟政, 韦喜忠, 李 鹏

中国船舶科学研究中心, 江苏 无锡 214082

0 引 言

在有闭式试验段的水洞中进行回转体通气超空泡试验时，存在试验段固壁对试验结果的影响问题，即所谓“壁面效应”。对于闭式试验段，壁面影响主要表现在2个方面：一是因试验段内壁与模型(或空泡)表面对流动的几何约束而引起的局部加速或静压降低现象，使得试验环境与原型有很大的不同，严重者甚至会引起“流动阻塞”；二是由于沿试验段轴向的压力梯度的存在，使得在试验中只能得到一个空化数分布，空泡形态、水动力系数、通气系数等重要的试验结果均对应于这个空化数分布，而在原型中只存在一个确定的空化数，将试验中的空化数分布修正到原型空化数是一个非常关键的问题。

对于壁面影响问题，国内外学者针对空泡流阻塞作了较多的研究，得到了一些重要的结论。Birkhoff等[1]以无升力楔形体的阻塞空泡流为研究对象进行了理论分析，结果表明传统试验中定义的阻力系数对洞壁距离的影响十分敏感。Wu等[2]采用不同的闭合模型，对闭式水洞中二维空泡流的外形和阻力系数进行了理论求解，并加以修正以适用于相应的无界流动。Guzevsky[3]采用势流理论，给出了不同锥角圆锥空化器所对应的阻塞空化数的计算公式。陈鑫等[4]基于均质平衡多相流理论和输运方程类空化模型，通过求解混合介质的RANS方程、RNGk-ε湍流输运方程和各相的质量输运方程，数值模拟了闭式水洞中带圆盘空化器航行体模型的定常通气空泡流动，分析了闭式水洞中洞壁效应对通气空化数、压力分布

分布规律、空泡尺寸以及模型阻力系数的影响。

本文以超空泡横截面独立膨胀原理作为理论基础，重点关注试验段沿程压降对空泡形态的影响，推导水洞试验段压力环境下空泡形态的理论计算公式，分析试验段沿程压降对空泡形态的影响规律。基于推导的公式，进一步分析模型阻塞比对空泡形态的影响，给出试验模型缩尺比的理论确定方法。最后，本文将给出试验中实测空化数与原型空化数的理论换算方法。

1 水洞试验段沿程压降对空泡形态的影响

图1给出了水洞试验段内超空泡流动示意图，并标出了主要物理量。Paryshev[5]介绍了Logvinovich给出的具有一般意义的空泡横截面独立膨胀原理：

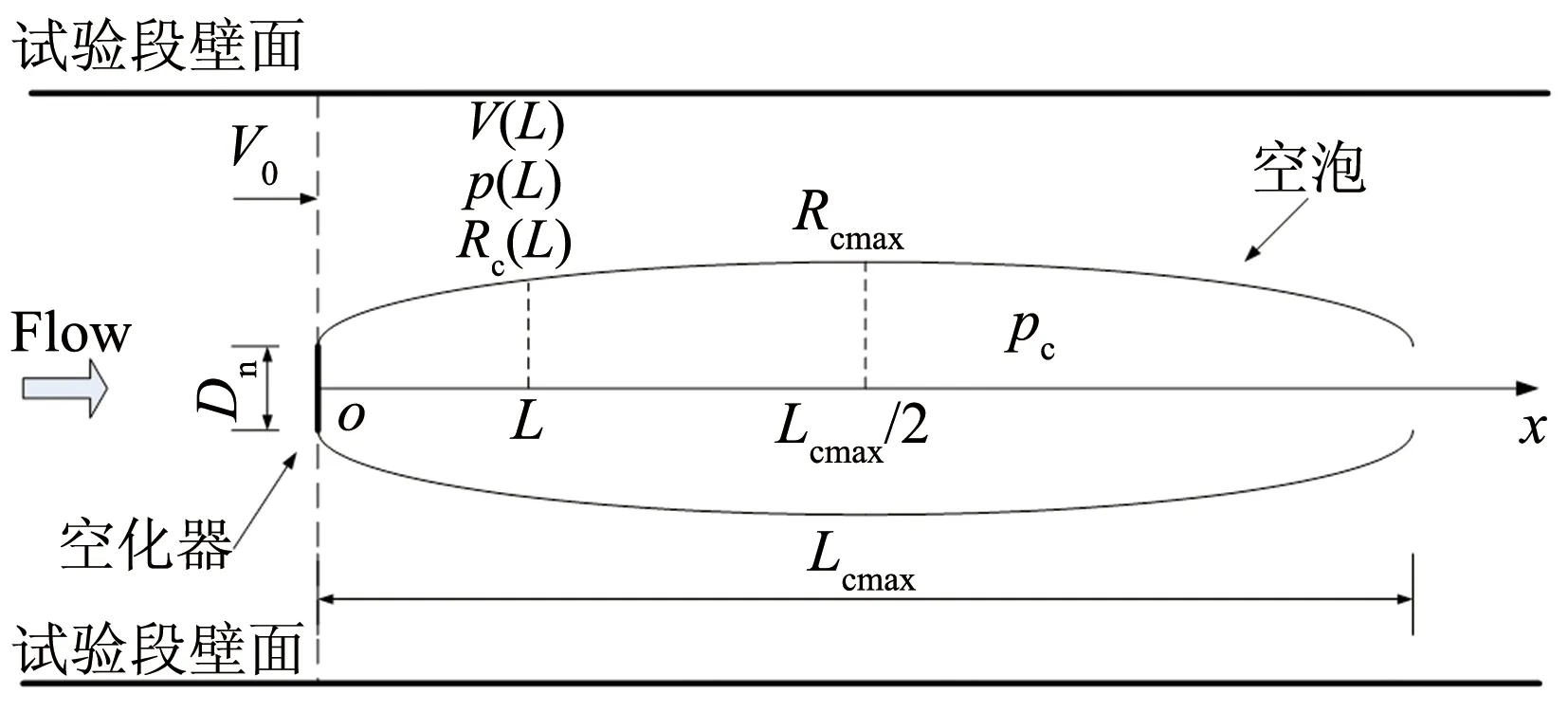
图1 试验段内超空泡流动示意图Fig.1 Sketch map of supercavitating flows in working section

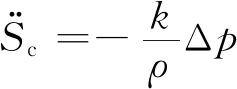
(1)

根据式(1)可导出无界流中的空泡横截面积表达式(上标“*”表示无界流)：

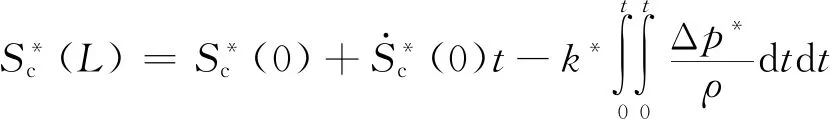
(2)

式中，L为空化器到计算横截面的距离(轴向距离)。在定常状态下，即环境压力p∞为常数时，式(2)可进一步简化：

(3)

考虑到t=L/V，式(3)可重写为：

(4)

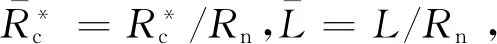
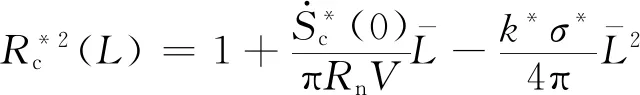
(5)

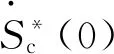
(6)

式中:CD为空化器阻力系数，取决于空化器锥顶角和空化数；a为一个弱依赖于空化数的系数。Vasin[6]给出了其范围为a=1.5～2.0，则式(5)可简化为：

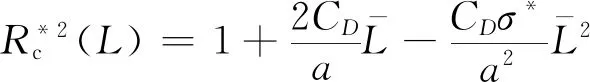
(7)

Guzevsky给出了空化器阻力系数的精确表达[7]：

(8)

式中，β为空化器锥顶角(rad)，CD0为零空化数下的空化器阻力系数。

在以上分析的基础上，进一步考虑水洞试验环境下的空泡发展。由于沿程压降的存在，参考压力是一个沿x轴的分布p(x)。仍假定泡内压力pc为定值，则空泡内外压差也是一个沿x轴的分布Δp(x)，且Δp(x)=p(x)-pc。

考察试验段入口、空化器处和任意截面L处的水速，有连续方程：

S∞V∞=(S∞-Sn)V0=[S∞-Sc(L)]V(L)

(10)

式中，S∞为试验段横截面积，Sn为空化器面积。一般来说，S∞≫Sc(L)>Sn，故本文假设V(L)≈V0。考虑沿程压降系数λ，则p(L)的表达为：

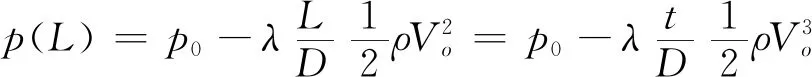
(11)

式中，D为试验段等效直径。结合式(7)得：

(12)

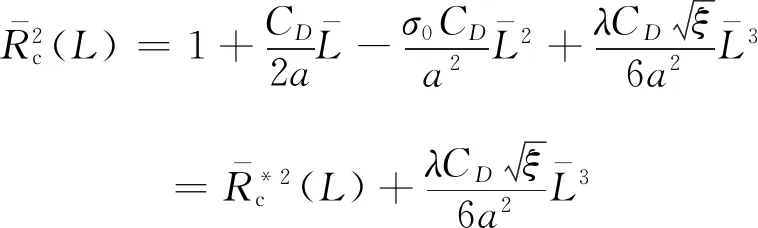
(13)

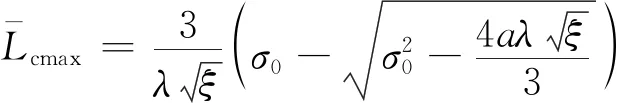
(14)

比较式(7)和(13)可以发现，相对于无界流而言，闭式水洞内的空泡轮廓多了与沿程压降系数、轴向距离和阻塞比相关的一项。

以圆盘空化器为算例，取CD0=0.815，a=2.0，空化器处的空化数为σ0=0.02，分别计算无界流和不同沿程损失系数闭式试验段内的空泡轮廓，如图2所示。可以看出，随着沿程损失系数的增大，空泡长度和空泡最大直径均呈递增趋势，但空泡长度的变化更为显著。

图2还表明，在同样的空化器当地空化数和压降系数下，阻塞比越大，空泡长度和直径也越大。当阻塞比达到某一临界值后，空泡无法在轴线上闭合，形成“开式空泡”。分析式(14)，可得到一个形成“闭式空泡”的判据：

图2 沿程压降对空泡形态的影响(σ0=0.02)Fig.2 Influence of longitudinal pressure gradient on cavity shape

(15)

2 实测空化数与原型空化数的理论换算

在水洞超空泡试验中，沿程压降的存在，使得在试验段轴向不同测点处测得的静压是一个空间上的分布p(x)。而试验中，试验水速V∞则是在试验段入口处测得的。故试验得到的空化数也是一个分布：

(16)

而在航行器实航情况下，空化数则是一个定值σ*。因此，需要将实测空化数分布换算为原型空化数。

超空泡航行器的水动力主要取决于空泡与航行体物面的相对位置，在不考虑弗劳德数对空泡影响的情况下(高速航行)，空泡长度成为决定水动力的主要因素。本文要处理的问题是：在试验状态和实航状态空泡(无量纲)长度相同的情况下，找到实测空化数分布与原型空化数的对应关系是什么？

运用式(9)和(14)，得到换算关系：

(17)

式中，ξ为模型阻塞比，λ为沿程压降系数测量值，系数a=2.0，σ0为空化器处的空化数。

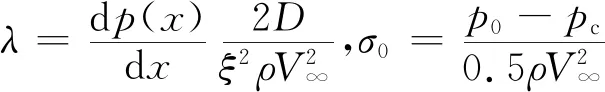
(18)

考察式(17)发现，当ξ→0时，σ*→σ0，即对应无界流情况。

3 理论修正公式的试验验证

调节通气流量以改变空泡尺度。试验过程中，采用高速摄影机拍摄空泡形态，图3给出了试验中获得的不同长度的空泡照片。

图3 验证试验中的空泡照片Fig.3 Cavity shape in tests

根据试验结果，可按式(17)计算出不同空泡长度所对应的不同的原型空化数。为验证式(17)，需要掌握无界流条件下空化数σ*与空泡长度的关系。乌克兰学者[8]根据前苏联自由航行试验(见图4)给出了空泡轮廓经验公式：

图4 俄罗斯自由航行试验照片Fig.4 Cavity shape in free-fly test (Russia)

(19)

上式的适用范围为：0.012<σ<0.057，根据式(19)能够容易地得到空泡长度与空化数之间的关系：

(20)

图5 公式(19)与验证试验照片的对比Fig.5 Comparison between the test cavity shape and formula (19)

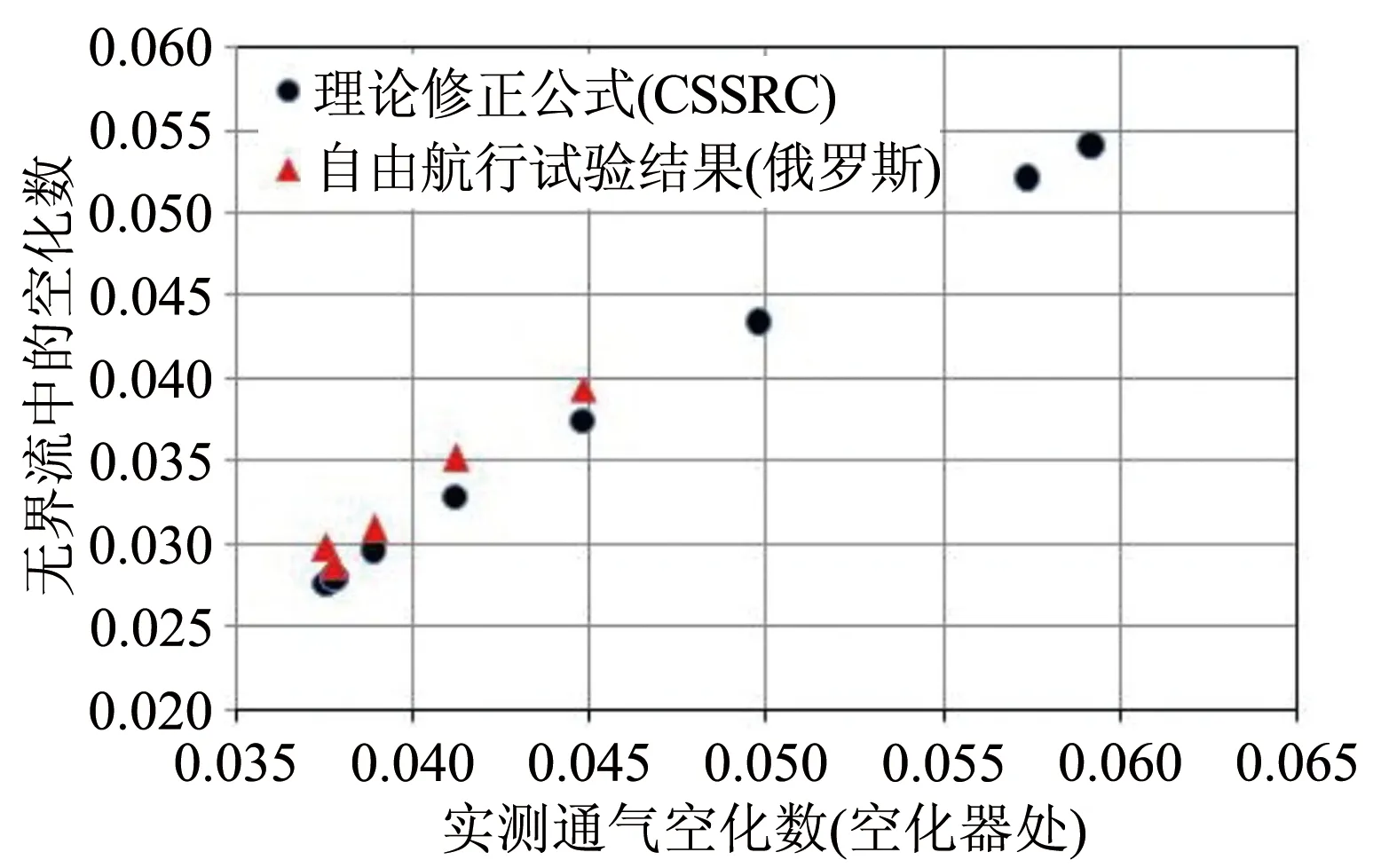
图6 理论修正公式与试验值的对比Fig.6 Comparison between the test results and theoretical results

4 结 论

本文基于空泡独立膨胀原理的基本思想，分析了超空泡水洞试验条件下试验段壁面对空泡形态的影响，并对空化数进行了修正。

1) 在同样的空化器处的空化数和沿程压降系数下，阻塞比越大，空泡尺度也越大。当阻塞比达到某一临界值后，空泡无法在轴线上闭合，形成“开式空泡”。

2) 给出了将实测空化数换算到原型空化数的理论修正公式，并得到了试验验证。