单摆小球在三维空间中运动规律研究

姜付锦 李 都 刘 颖

(湖北省武汉市黄陂区第一中学，湖北 武汉 430300)

在高中阶段,单摆小球在二维空间中的运动形式主要有两类:单摆运动(简谐运动)和圆锥摆运动(匀速圆周运动)．小球开始做圆锥摆运动,若小球的初速度有一个微扰,则小球会不会再次达到匀速圆周运动?[1][2]小球会不会做椭圆摆运动?[3]研究表明小球既不做匀速圆周运动,也不做椭圆摆运动,而是一种复杂的三维曲线运动．

1 什么是椭圆摆运动?

文献[4-5]已明确指出: 如图1所示,一个质量为m1、半径为R的半球形光滑凹槽放置在光滑水平上,再将一个质量为m2的质点置于凹槽内角度为θ处,质点由静止状态自由下滑,可以证明,质点相对地面静止参考系的运动轨迹是椭圆线,故该系统是一种典型的椭圆摆系统．若半球形光滑凹槽固定,则质点的运动轨迹不可能是椭圆摆．

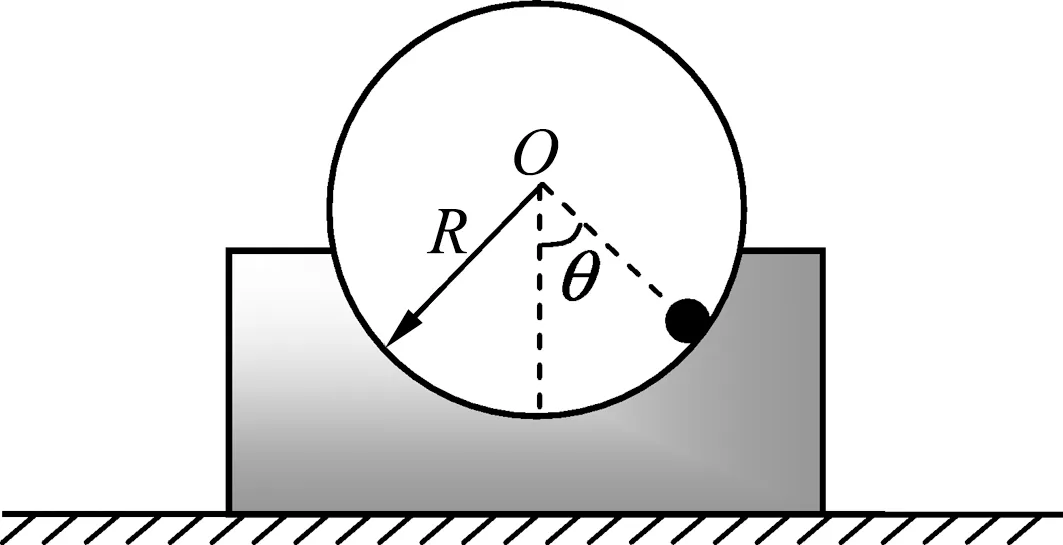
图1 椭圆摆系统

2 为什么小球不能再次做匀速圆周运动?

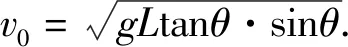
图2

(1)

相对于竖直轴的角动量守恒

mαv0Lsinθ=mvmLsinθm.

(2)

联立(1)(2)两式可求得

(3)

通过研究可以发现,若α=1,则小球做匀速圆周运动;若α>1,则(3)式求的是小球运动过程中最小速度;若α<1,则(3)式求的小球运动过程中最大速度;当α≠1时,则小球将在半径为L的球面上做复杂的周期性运动,它不可能做匀速圆周运动．

3 小球的动力学微分方程组

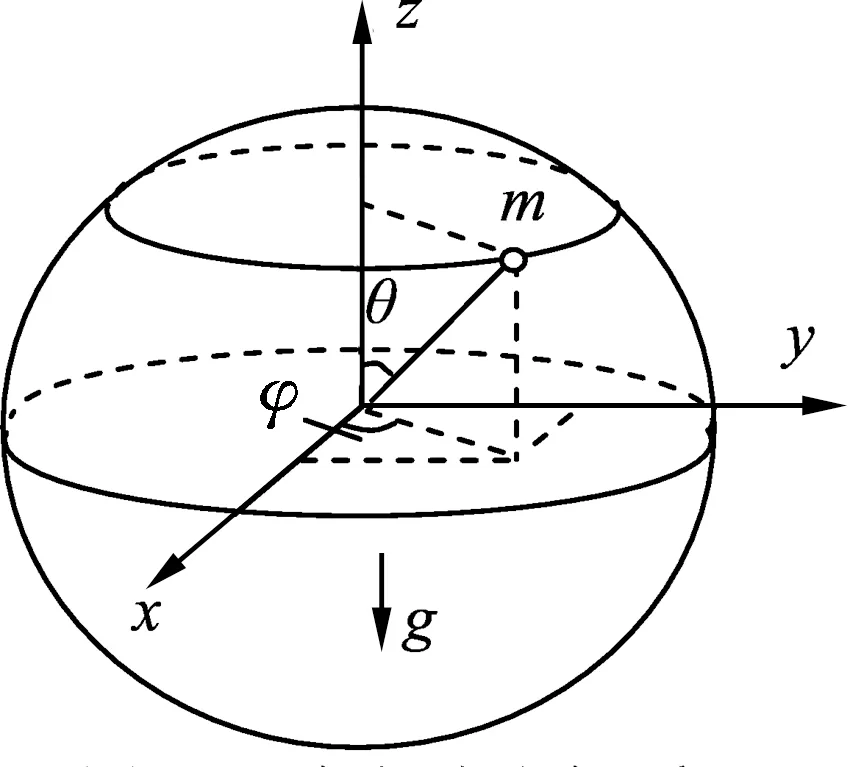
图3 建立球坐标系

通过小球的受力分析可知

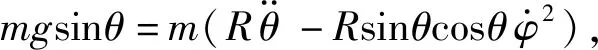
由以上两式求得

(4)

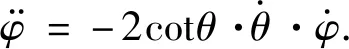
(5)

3.1 小球在经线方向上微扰周期

小球对竖直轴角动量守恒,则有

(6)

(6)式中L为小球的角动量,θ0为开始时绳子与Z轴的夹角,ω0为小球匀速圆周运动的角速度, 联立(4)、(6)两式得

(7)

设θ=θ0+δ,δ→0,π/2<θ0<π,则有

(8)

联立(7)、(8)两式得

(9)

将(9)式整理后得

(10)

将sin-3(θ0+δ)展开为泰勒级数形式,并舍去二阶及以上的小量得

(11)

将(6)、(11)两式代入(10)式得

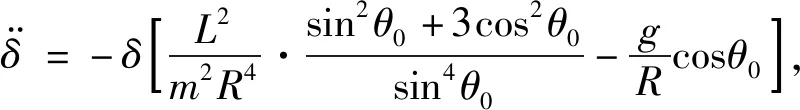
(12)

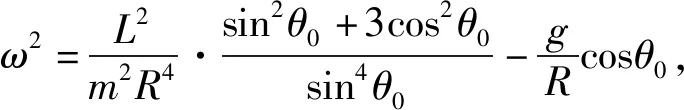
(13)

开始时小球做匀速圆周运动,则

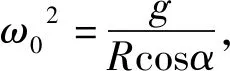
(14)

联立(6)、(13)、(14)3式得

(15)

结合小球在经向初始状态,求解(12)式得小球沿经线微扰规律和周期分别为

(16)

3.2 小球在纬线方向上微扰周期

小球对竖直轴角动量守恒,则联立(6)(8)两式整理得

(17)

将sin-2(θ0+δ)展开为泰勒级数形式,并舍去二阶及以上的小量得

(18)

把(18)式代入(17)式得

(19)

将(14)式代入(19)式后得

(20)

再对(20)式求导得

(21)

联立(12)、(13)、(16)、(21)4式得,小球在纬线方向圆周运动微扰角加速度与时间是简谐振动关系,且与小球在经线方向微扰振动周期相等,所以小球在纬线方向微扰角加速度振动规律和周期分别为

(22)

3.3 数值模拟

3.3.1 小球微扰运动轨规律

当小球微扰角速度为0.9792ω0时,小球的运动轨迹是闭合周期解,运动轨迹在水平面上的投影近似一个较粗的圆环,最外侧与最内侧相距很近;两幅侧视图完全相同,都是轴对称图形,证明了小球运动轨迹具有闭合周期性特征;小球在3个方向上都做简谐振动,在X轴与Y轴方向上的振动周期相等,且TX∶TY∶TZ=4∶4∶3,所以图5和图6是尼萨如图形．

图4 X-Y关系

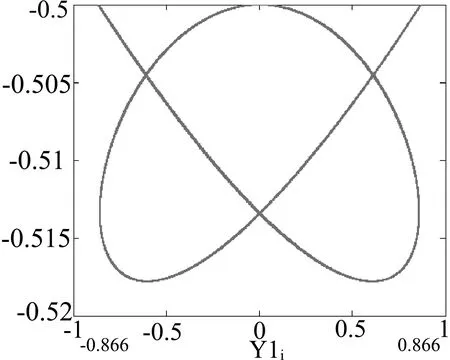
图5 Z-Y关系

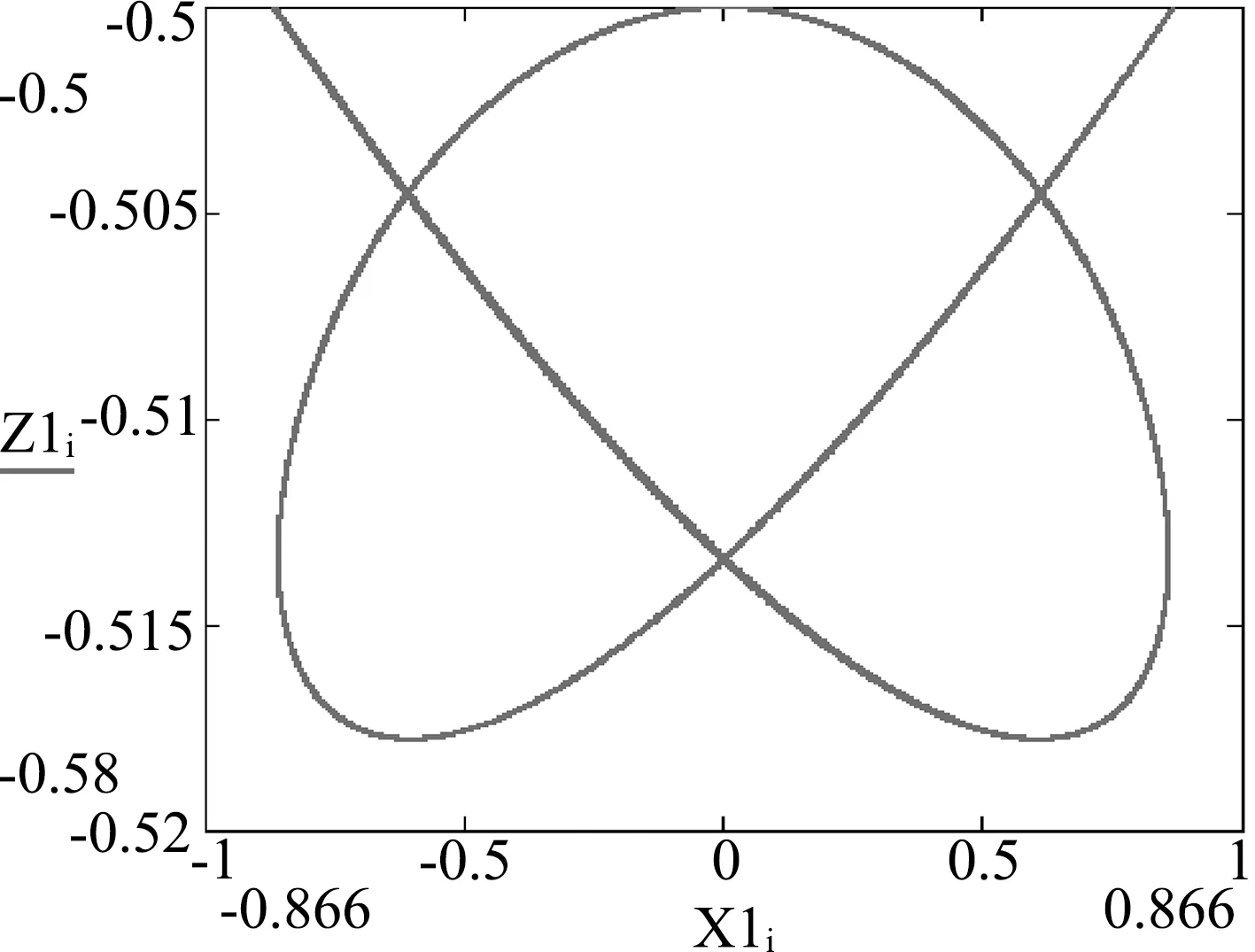
图6 Z-X关系

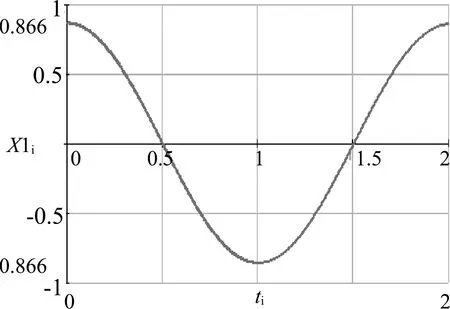
图7 X-t关系

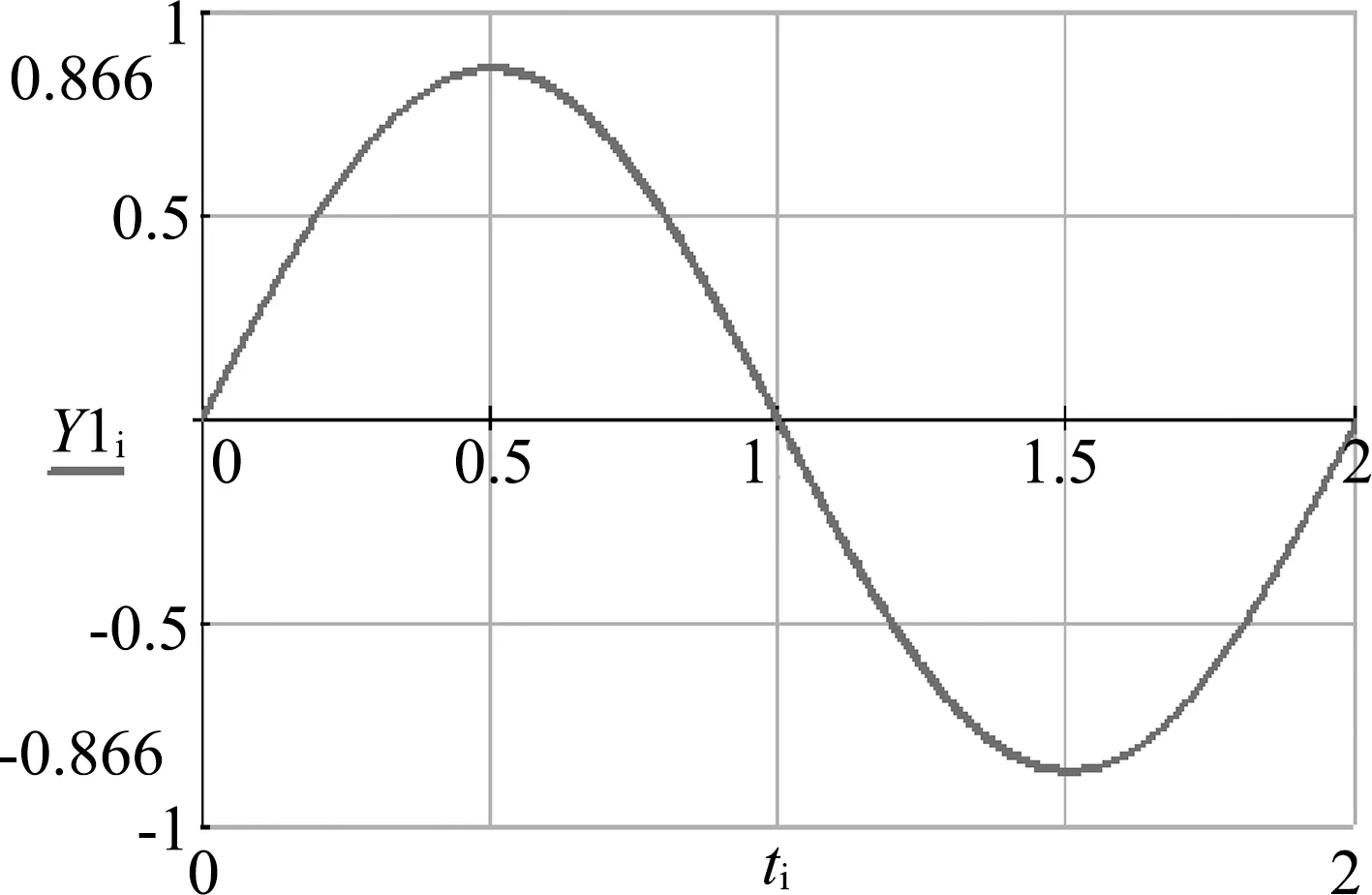
图8 Y-t关系

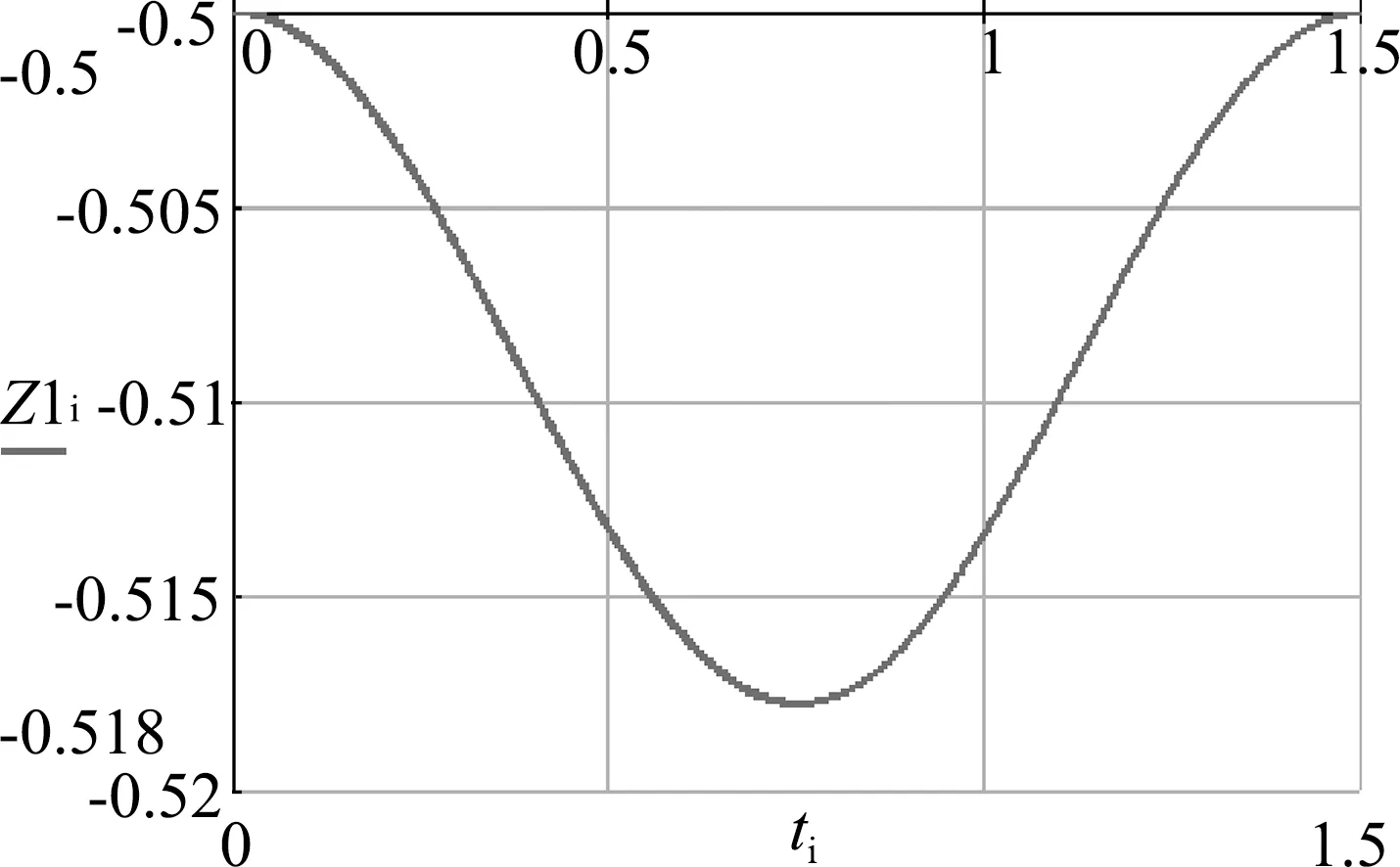
图9 Z-t关系

3.3.2 小球微扰时在经线方向与在纬线方向上振动规律

小球微扰角速度为0.9792ω0,由图10、图12可以看出在经线方向和在纬线方向两个角速度的振动周期相同,这与(16)、(22)两式分析结果吻合;因为经线方向小球角速度与角度的振动相位差是π/2,所以在经线方向角速度与经角的相图是一个椭圆;因为经线方向小球角加速度与纬向角加速度的振动相位差是π/2,经向角加速度与纬向角加度相图也是一个椭圆．

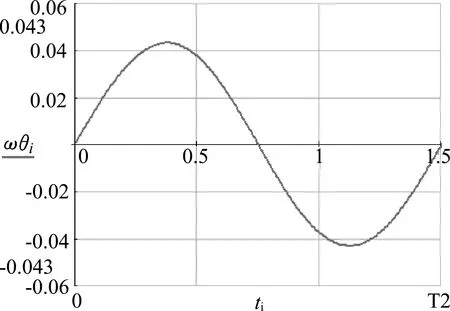
图10 经向角速度与时间关系

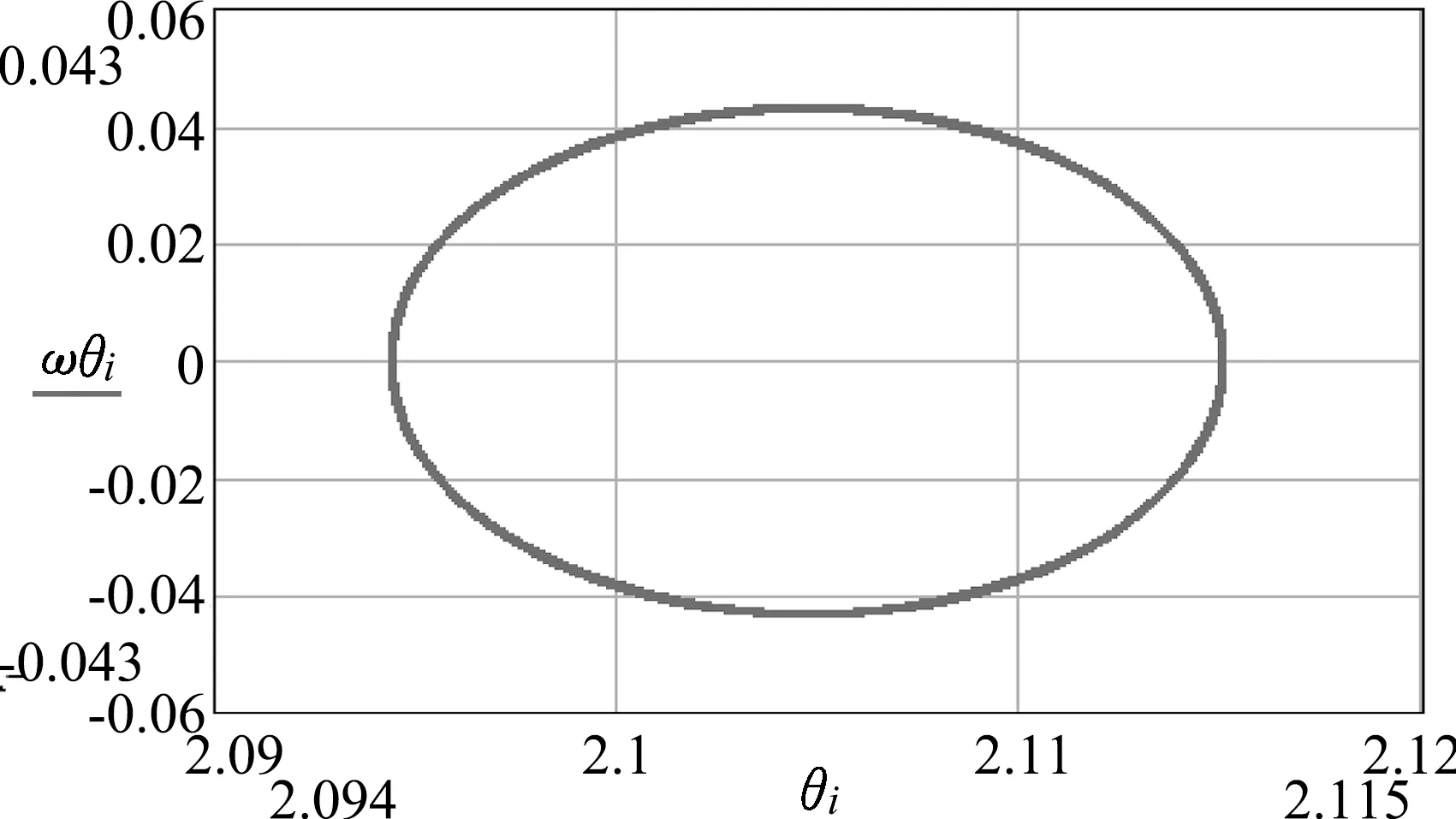
图11 经向角速度与经角相图

图12 纬向角加速度与时间关系

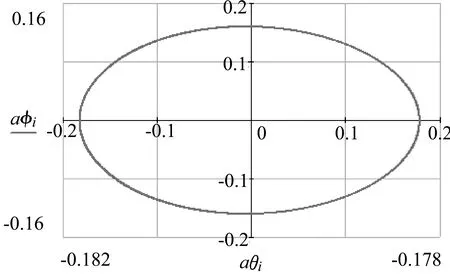
图13 纬向角加速度与经向角加速度相图

3.3.3 一般运动情况下闭合周期轨迹的三视图

当小球初角速度为1.09 r/s时,其运动轨迹也是一组闭合周期性解,其在水平面上的投影很像“水星近日点进动”现象,[7]其中最外侧与最内侧分别对应小球运动的最高点和最低点,数值模拟结果也与(3)式分析结果吻合;两幅侧视图也完全相同,满足轨迹闭合周期解的基本特征．若小球在纬线方向和在经线方向上运动周期之比恰好是有理数,则小球在三维空间的运动轨迹是闭合周期解[8]．

4 结语

若小球受到的合外力恰好可以提供匀速圆周运动向心力,则小球做匀速圆周运动;若小球在匀速圆周运动时速度有微扰,则小球不会再次达到匀速圆周运动状态[9],而且小球在经线方向与在纬线方向上两个角速度振动周期相等,若微扰角速度满足一定条件,则小球运动轨迹的侧视图可能是尼萨如图形;若小球开始时不做匀速圆周运动,则小球的运动轨迹将是一种复杂三维曲线(球面摆),其俯视图不是椭圆,其水平投影被限制在两个圆周之间所夹的“环状”区域,轨迹形状类似“水星近日点进动”现象[7],在经线方向和在纬线方向上都是周期性运动;若小球在纬线方向和在经线方向上两个运动周期之比恰好是有理数,则小球在三维空间的运动轨迹是闭合周期解[8],如图14、图15和图16所示;参考文献[3]中之所以会出现所谓的“椭圆”,其实并不是真正的“椭圆”,它只是图14中某一小段时间内的运动轨迹水平投影,与椭圆类似而已;当单摆的悬点是固定时,小球不可能做“椭圆摆”运动．

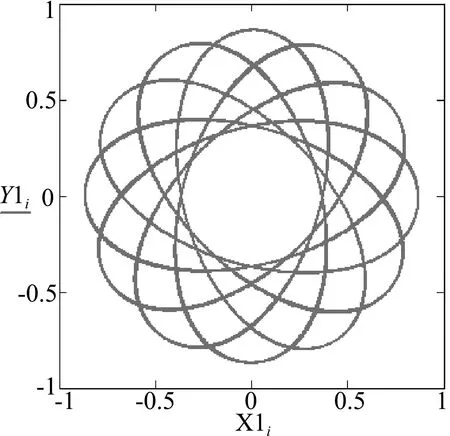
图14 Y-X图

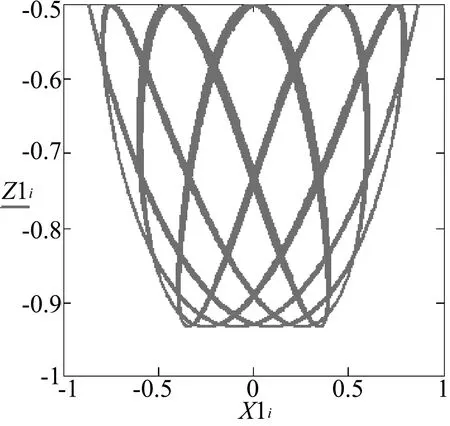
图15 Z-X图

图16 Z-Y图