利用圆的性质解决力学中动态平衡问题
2021-05-15任致远
何 勇 任致远
(新疆兵团二中,新疆 乌鲁木齐 830002)
高中物理无论是力学、热学,还是电学中,动态平衡问题会被经常用来考查学生对物理问题理解能力、知识迁移能力,分析推理能力、综合运用能力和利用数学知识解决物理问题的能力.在力学问题中动态平衡,我们往往常用的有图解法和解析法.这里我们将利用圆的相关性质,结合“三角形相似”、“正弦定理”和“辅助圆”解决一些与圆相关的动态平衡问题.
1 利用三角形相似处理动态平衡
例1.如图1所示,固定在竖直平面内的光滑圆环的最高点有一个光滑的小孔.质量为m的小球套在圆环上.一根细线的下端系着小球,上端穿过小孔用手拉住.现拉动细线,使小球沿圆环缓慢上移.在移动过程中手对线的拉力F和轨道对小球的弹力N的大小变化情况是
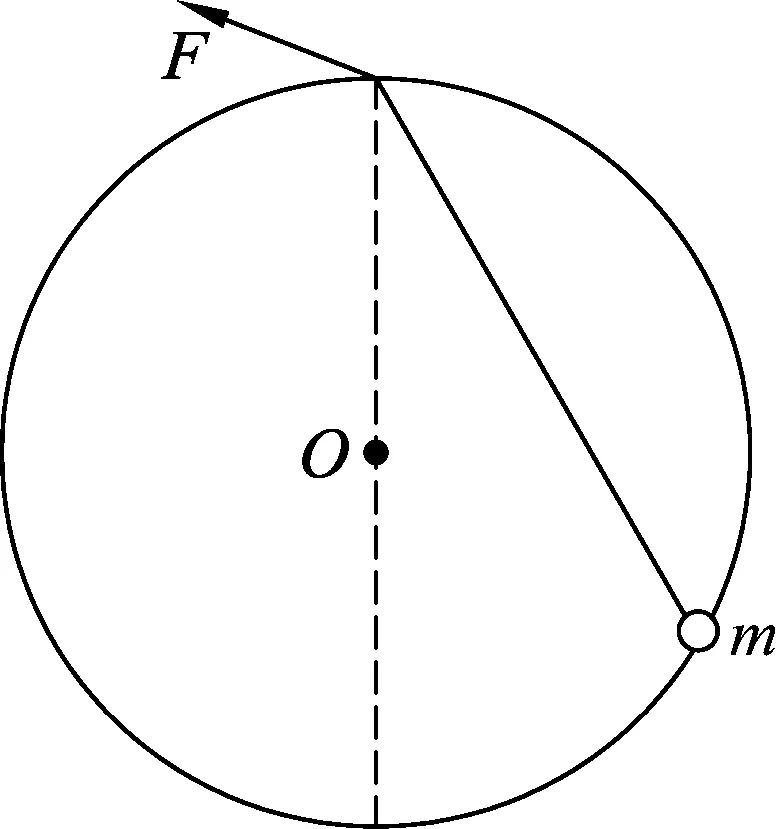
图1
(A)F不变,N增大. (B)F减小,N不变.
(C)F不变,N减小. (D)F增大,N减小.
在本题中,小球沿圆环缓慢上移,对小球进行受力分析时,我们发现它始终受到竖直方向重力G、沿细绳方向拉力F和沿圆半径方向弹力FN,这3个力满足受力平衡.作出受力分析图(图2),可知△OAB∽△GF′A

图2
在重力G,圆的半径R不变时;小球缓慢上移过程中,l逐渐变小,所以F逐渐减小.
2 利用正弦定理处理动态平衡
例2.如图3所示,ADB是一个光滑球面,AOB为水平直径,C为质量为m的光滑小球,小球通过过A点处的光滑定滑轮的轻绳拉住,现使小球C缓慢地从A点运动到处于O点正下方的D点处.重力加速度大小为g,关于小球C从A点运动D点的过程,下列说法正确的是
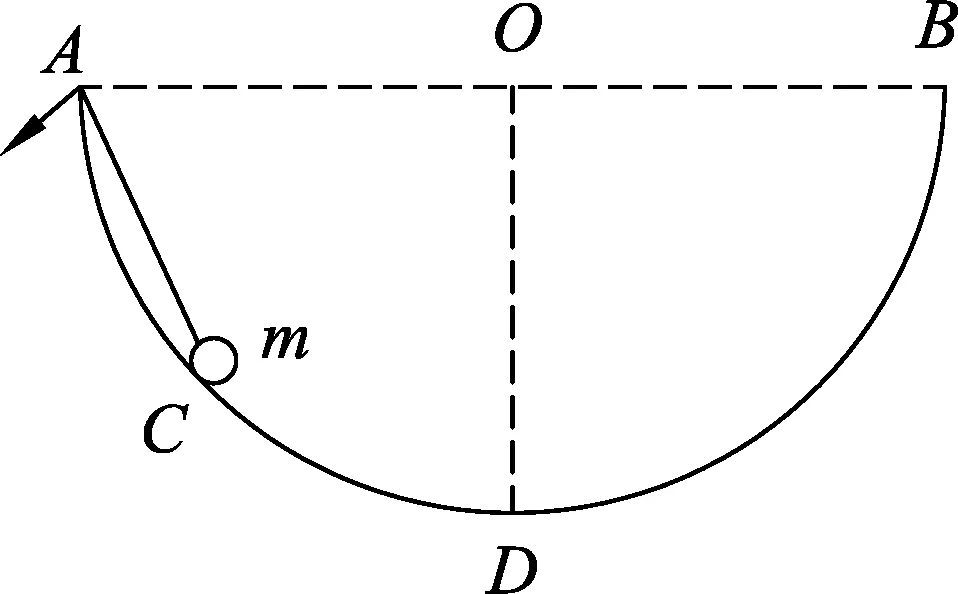
图3
(A) 绳对小球的拉力先增大后减小.
(B) 绳对小球的拉力逐渐减小.
(C) 光滑球面对小球的支持力先减小后增大.
(D) 光滑球面对小球的支持力逐渐减小.
在本题中,小球沿圆环缓慢上移,如图4,对小球进行受力分析时,我们发现它始终受到竖直方向重力G、沿细绳方向拉力F和沿圆半径方向弹力N,这3个力满足受力平衡.

图4

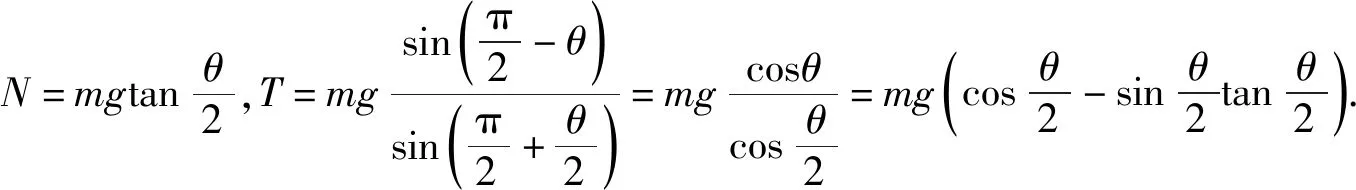
3 利用辅助圆通过图解法处理动态平衡

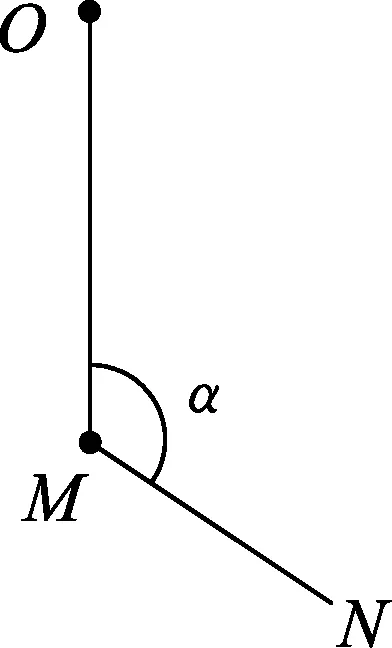
图5
(A)MN上的张力逐渐增大.
(B)MN上的张力先增大后减小.
(C)OM上的张力逐渐增大.
(D)OM上的张力先增大后减小.
对M处的重物进行受力分析,并将力平移至一个力的三角形中,如图6所示,重力大小方向不变,其所对的角为π-α也始终不变,作出这个三角形的外接圆,三力平衡构成封闭三角形,画其外接圆,利用圆周角不变解题.P在外接圆上移动,初始位置从重力末端直至图中Q点,利用图解法确定力FNM及FOM的变化情况.

图6
下面我们就3种方法来解决一个力学中动态平衡的问题.
应用:如图7所示为一种儿童玩具,在以O点为圆心的四分之一竖直圆弧轨道上,有一个光滑的小球(不能视为质点),O′为小球的圆心.挡板OM沿着圆弧轨道的半径,以O点为转轴,从竖直位置开始推着小球缓慢顺时针转动(水平向里看),到小球触到水平线的过程中:圆弧轨道对小球的支持力N1的变化?挡板对小球的支持力N2的变化?
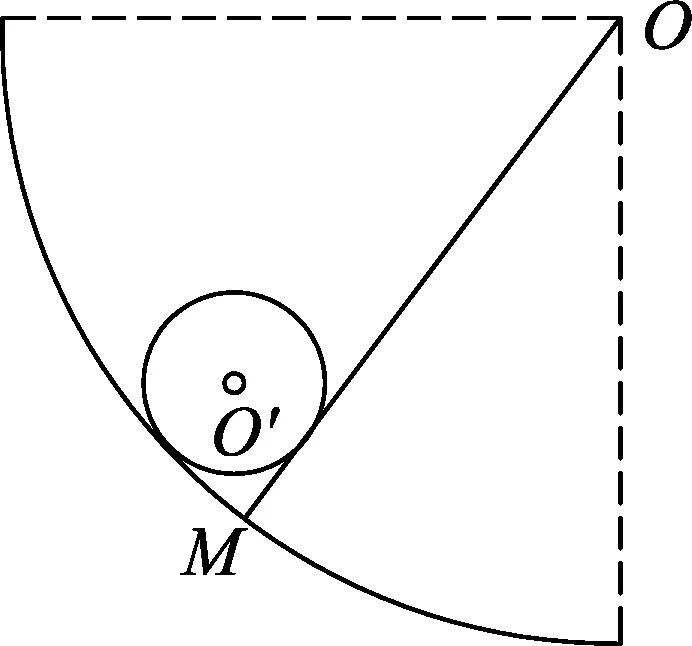
图7
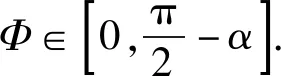
解法1:利用三角形相似(此法关键在于找到与受力三角形相似的三角形)延长N2作用力力线,交竖直线ON于A点,OM于B点,
根据图8受力的三角形与△OO′A相似,可得以下关系

图8



解法2: 利用正弦定理(此法关键在于找到与受力三角形,确定各力间的夹角)
根据图9力的三角形中边和对应角,由正弦定理可得
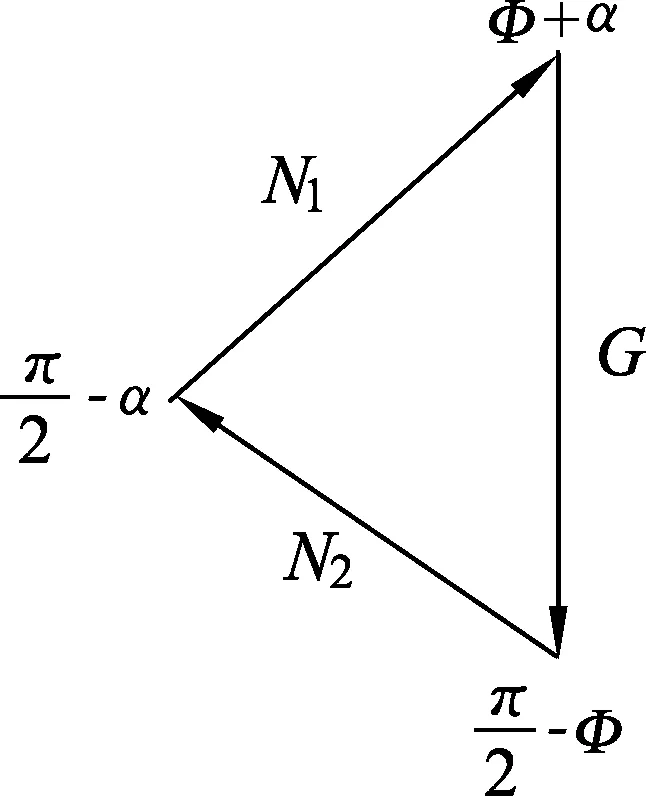
图9

图10

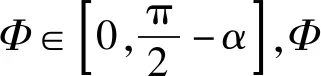
解法3:利用辅助圆通过图解法处理动态平衡
(此法关键在于中间有两个力的夹角必须不变)

以上几种利用圆的性质和特点,解决力学中的动态平衡问题的方法,有时也是相通的.在教学和考试中,只要把握住其中的关键信息和条件,指导学生选择适合自己理解的方法,都可以达到事半功倍的效果.
